大跨PC曲线连续刚构桥空间特性及收缩徐变影响分析

辛景舟，周建庭，王 宇，杨 茂

(重庆交通大学土木建筑学院，重庆 400074)



专家信息

大跨PC曲线连续刚构桥空间特性及收缩徐变影响分析

辛景舟，周建庭，王 宇，杨 茂

(重庆交通大学土木建筑学院，重庆 400074)

为明确曲线连续刚构桥的空间特性及收缩徐变对其产生的影响，文章以某大桥为工程背景，采用桥梁通用软件Midas/Civil建立空间有限元模型，分析了大跨PC曲线连续刚构桥最大悬臂阶段和成桥阶段主梁自重、预应力、混凝土徐变对主梁内力、关键截面应力及主梁空间变形的影响，同时考虑混凝土收缩徐变为长期效应，计算了随着服役期的增长收缩徐变对曲线连续刚构的影响规律，研究成果可为曲线连续刚构桥的设计和施工提供参考。

曲线连续刚构桥；弯矩；扭矩；应力；位移；收缩徐变；影响分析

0 引言

近年来，随着我国高速公路的发展，尤其是山区高速公路的大规模建设开发，曲线连续刚构桥由于其在线形适应性、跨越能力、经济性、整体性能、造型美

观性、施工便易性等诸多方面表现出的突出优势而得到了广泛应用[1]。与直线刚构桥相比，曲线连续刚构桥由于弯扭耦合作用的存在，空间受力与变形更加复杂[2]。因此，研究曲线连续刚构桥空间受力与变形特性，具有较强的理论与现实意义。

随着曲线连续刚构桥的修建，已有学者对其开展了相关研究。李新春等通过参数变异改变某曲线连续刚构桥的曲率半径，分析研究了结构自重、施工挂篮、预加力以及混凝土收缩徐变对桥梁悬臂施工过程中预拱度设置的影响，为曲线刚构桥悬臂施工预拱度的设置提出了科学建议[3]；褚文涛等以大跨S形曲线连续刚构桥为研究对象，分析了自重、收缩徐变、预应力荷载对成桥结构径向位移的影响，同时，计算了静风荷载作用下大悬臂的径向位移，并针对在最不利风载工况下该桥的两幅桥有可能会发生横向碰撞，提出了建议措施[4]；郭凡等结合工程实例，建立有限元模型计算分析高墩曲线刚构桥的受力和位移规律[5-6]；杨孟刚等以实际工程为依托，通过建立空间有限元模型，计算得到不同荷载作用下的主梁扭矩分布，得到了采用预应力筋的不对称张拉以及不对称布筋方式能有效抵消恒载产生的扭矩的结论[7]。尽管相关研究已经开展，然而，针对考虑长期效应的收缩徐变对曲线刚构桥影响的研究却相对较少。

基于此，本文以某大跨PC曲线刚构桥为工程背景，建立空间有限元模型，在全面分析曲线刚构桥最大悬臂施工阶段和成桥阶段主梁线形和内力特性的基础上，计算研究了混凝土收缩徐变对曲线连续刚构桥的影响，得出了混凝土收缩徐变对曲线连续刚构桥影响的具体规律，研究成果可为曲线连续刚构桥的设计和施工提供参考。

1 工程实例与有限元模型

某桥为单箱单室曲线连续刚构桥，跨径布置为(61+104+61)m，双幅布置，内幅平曲线半径仅为340.85 m，横向坡度为5%，顶底板横坡与路线横坡保持一致。主梁采用C60混凝土，箱梁顶板宽11 m，底板宽6 m，两侧翼缘悬臂长2.5 m，根部梁高6 m，跨中梁高2.3 m，箱梁高度按1.8次抛物线变化。主桥采用对称悬臂浇筑施工。纵桥向按全预应力混凝土设计，横桥向按部分预应力A类构件设计。主桥上部结构采用三向预应力，合龙顺序按先边跨后中跨考虑。

空间有限元模型采用Midas/Civil软件建立，模型立面、平面图如图1所示。因桥宽较窄，故采用单梁方法建立模型，桥墩、主梁均采用梁单元。模型不考虑横坡、纵坡影响，按平桥进行计算。主梁根据施工顺序和截面变化节点进行结构离散(对墩的划分进行了简化)，共划分为84个单元，其中上部结构划分为68个单元，下部结构划分为16个单元。为简化计算，不考虑承台以下基础变形，墩底固结。

(a)立面图

(b)平面图

2 空间特性计算结果及分析

大跨PC曲线连续刚构桥空间受力复杂，特别是在悬臂施工时，墩梁固结为T形静定结构体系，而当桥梁施工至边跨及中跨合龙时，结构将从静定体系转换为超静定体系。经历体系转换后，结构发生内力的重新分布。本文对曲线连续刚构桥主梁结构受力行为的分析，从主梁内力、主梁截面应力及主梁位移三方面展开。同时，为方便对比，选取主梁最大悬臂施工阶段、全桥合龙施加二期恒载后两个阶段进行分析。

2.1 主梁内力

最大悬臂阶段和成桥阶段主梁弯矩分别如图2、图3所示。弯矩以截面下侧受拉为正，上侧受拉为负；模型平面图(图1-b)中整体坐标轴原点位置为1#节点，主梁节点编号沿X方向依次增大至69#。

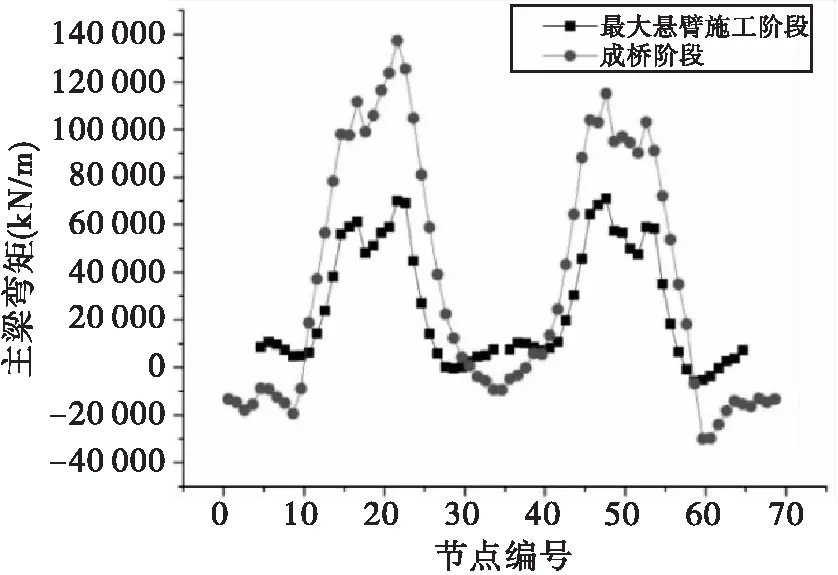
图2 最大悬臂阶段及刚成桥阶段主梁弯矩图

由图2可知，最大悬臂施工阶段，两悬臂结构为静定状态，且相互独立，两T构纵向弯矩变化趋势相近，只是数值略有不同，两T构最大纵向弯矩分别为69 239.33kN/m和70 136.79kN/m，最大弯矩位置均出现在中跨悬臂根部，而不是在墩顶中间，这主要是双薄壁墩的影响造成的；主梁大部分均承受正弯矩，只有较小范围承受负弯矩，且负弯矩绝对值较小。全桥合龙后，两相互独立的悬臂T构连成整体，结构转换为超静定结构，主梁内力重新分布，两边跨端部至1/4lbk(边跨跨径)及主跨跨中约1/8lzk(主跨跨径)范围内主梁截面承受负弯矩，其他截面承受正弯矩，负弯矩绝对值同最大悬臂阶段相比，有所增大，绝对值最大为30 681.1kN/m；最大弯矩位置依然出现在中跨悬臂根部，达136 503kN/m。

曲线桥由于超高的设置，造成截面的外侧尺寸大于内侧尺寸，中心轴偏离截面中心，扭矩由此产生[7]。此外，预应力筋的张拉、外荷载的偏心作用也可产生扭矩。本文计算了合龙成桥阶段各种荷载作用下主梁的扭矩，计算结果见图3。

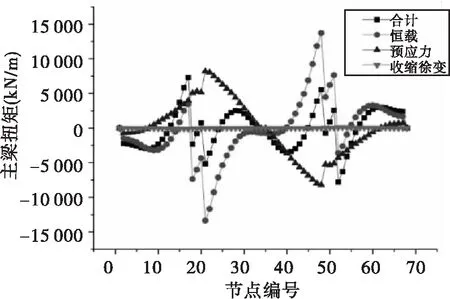
图3 成桥阶段主梁扭矩图

由图3可以看出，恒载作用对主梁扭矩产生的影响最大，预应力荷载其次，收缩徐变影响最小；由恒载引起的扭矩分布曲线与总的扭矩分布变化曲线相近，各种荷载引起的扭矩在全桥范围均近似呈反对称分布。

2.2 主梁截面应力

曲线连续刚构桥各关键截面的4个计算点位置在最大悬臂阶段和成桥状态下的应力值见图4及表1。

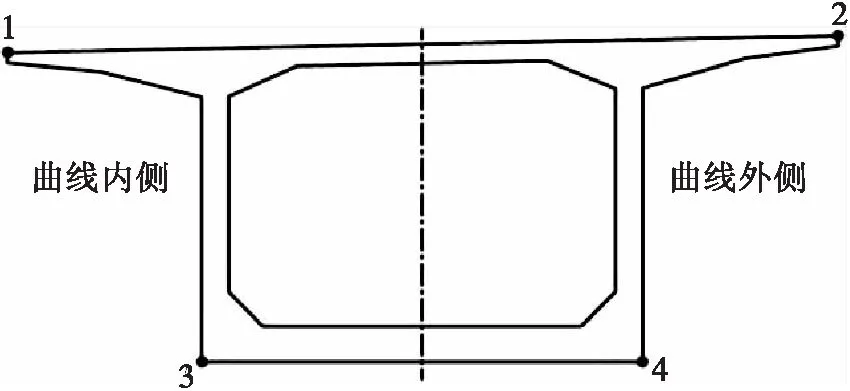
图4 截面计算点位置示意图

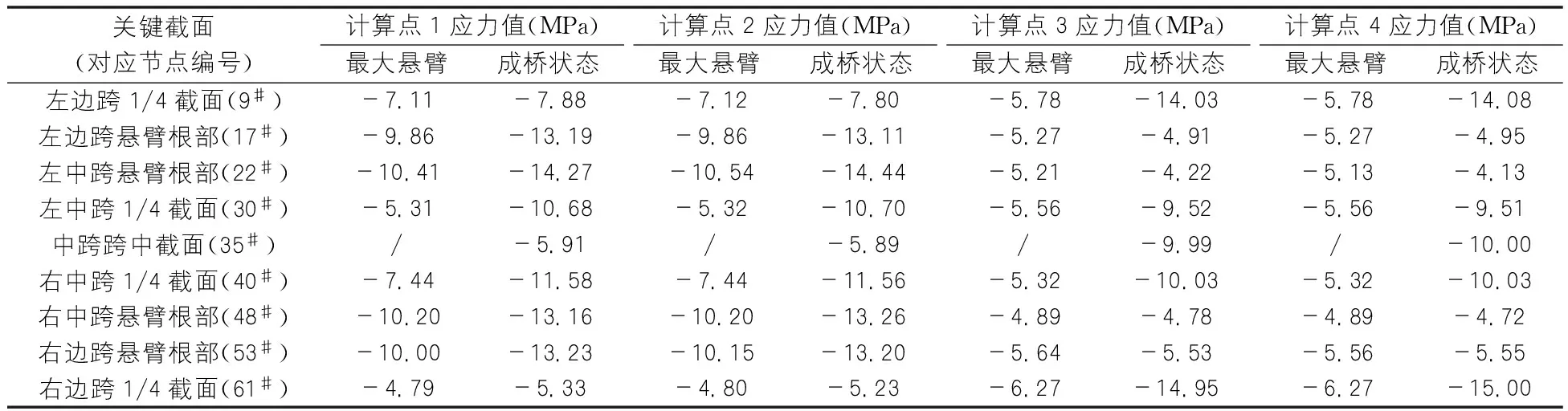
表1 最大悬臂阶段和成桥阶段关键截面应力计算值表

由表1可以看出，纵桥向各关键截面均承受压应力。最大悬臂施工状态，两T构中跨悬臂段根部截面应力最大，分别为10.54MPa、10.20MPa，顶板压应力大于底板压应力；进入成桥阶段，结构发生体系转换，应力重新分布，主梁各关键截面均承受压应力；除9#、61#节点位置外，其他各关键截面顶板压应力大于底板压应力。

横桥向相同状态下，关键截面顶底板应力横向相差较小，最大差值仅为0.17MPa，出现在成桥状态左中跨悬臂根部顶板位置。

2.3 主梁位移

最大悬臂施工阶段、全桥合龙施加二期恒载后考虑恒载、预应力、收缩徐变等影响因素的主梁竖向位移曲线如图5、图6所示。

由图5、图6可以看出，两种状态下，恒载和预应力对主梁竖向变形影响效果相反，且均对竖向主梁有较大影响，在恒载与预应力荷载的共同作用下，主梁竖向位移保持在相对较小水平；最大悬臂状态下，最大竖向位移出现在悬臂中跨端部位置，下挠16.68mm；成桥状态下，主梁最大上挠值为49.1mm。

在恒载作用下曲线连续刚构主梁会产生扭矩，该扭矩传递给桥墩，引起桥墩的侧向弯曲，进而使得桥墩发生侧向位移[8]。而墩梁固结，保持变形协调，因此，曲线连续刚构桥即使在垂直荷载作用下其主梁也将发生径向位移。

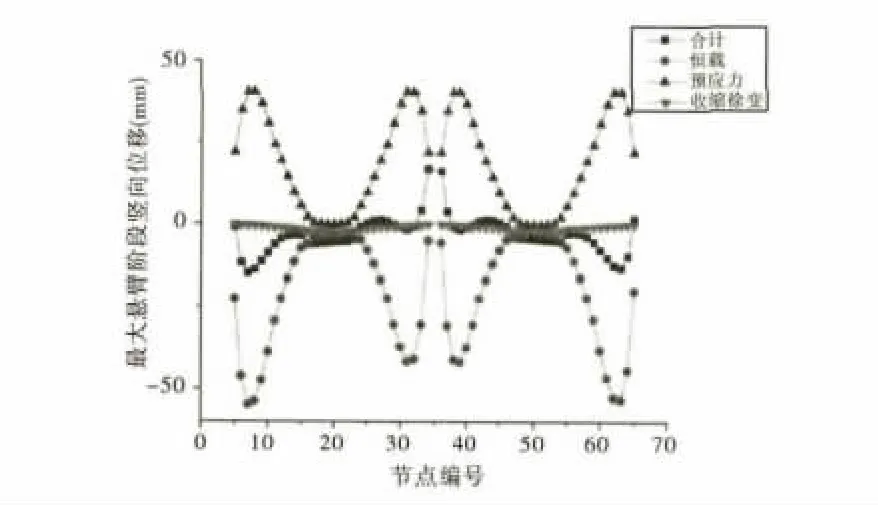
图5 最大悬臂施工阶段主梁竖向位移示意图

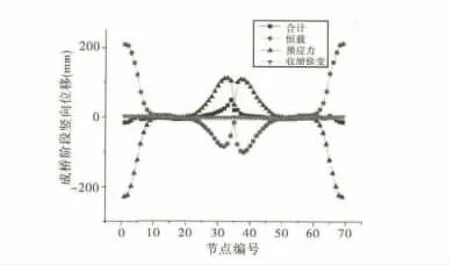
图6 成桥阶段主梁竖向位移示意图

最大悬臂施工阶段、全桥合龙施加二期恒载后考虑恒载、预应力、收缩徐变等影响因素的主梁径向位移曲线如图7、图8所示，径向位移正值指向曲线内侧、负值指向曲线外侧。

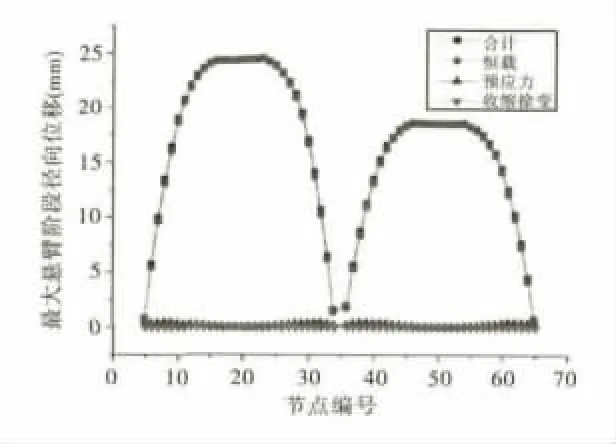
图7 最大悬臂阶段主梁径向位移示意图

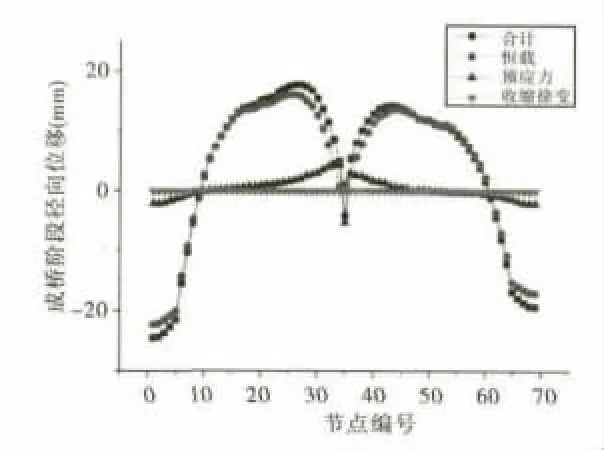
图8 成桥阶段主梁径向位移示意图

由图7、图8可以看出，曲线连续刚构径向位移主要由恒载提供，同悬臂状态相比，成桥状态下，预应力对主梁径向位移影响有所增大，但依然影响有限，收缩徐变影响最小，同恒载作用相比，其影响可忽略不计。

从数值上看，最大悬臂阶段主梁径向位移均指向曲线内侧，悬臂端径向位移较小，由悬臂端至主墩径向位移迅速增大，且两主墩附近达到最大值，在一定范围内，数值在24mm附近波动，据此特征可以判断：悬臂阶段主梁径向位移主要是墩向曲线内侧弯曲，带动梁体径向平行移动造成的。进入成桥阶段，结构转换为超静定整体，结构自由度下降，全桥主梁径向位移方向不再一致，两边跨梁端1/4跨径内径向移动方向指向曲线外侧，其余梁段指向曲线内侧。曲线外侧最大径向移动值为24.5mm，相反方向最大径向移动值为17.7mm。

同直线桥相比，曲线桥切线位移同样不容忽视。最大悬臂施工阶段、全桥合龙施加二期恒载后考虑恒载、预应力、收缩徐变等影响因素的主梁切向位移曲线如图9、图10所示，切向位移以如图1平面图所示自左向右为正。

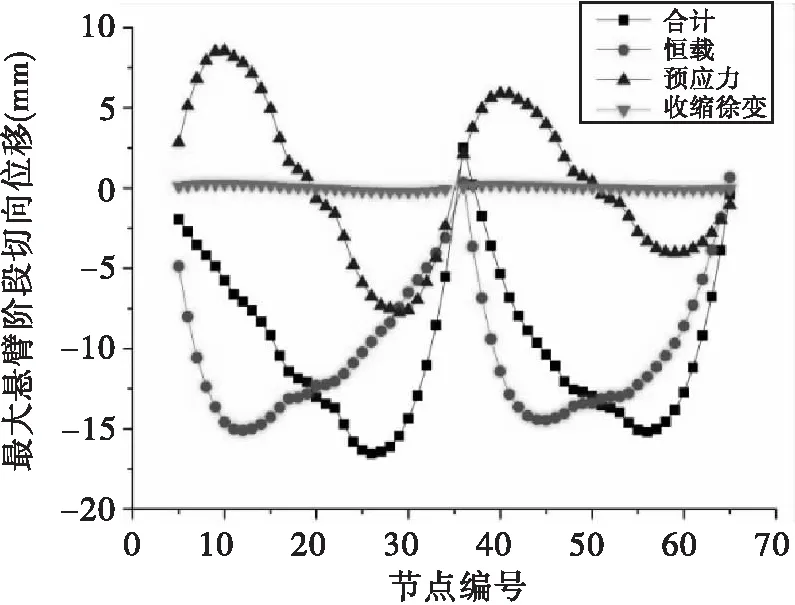
图9 最大悬臂阶段主梁切向位移示意图

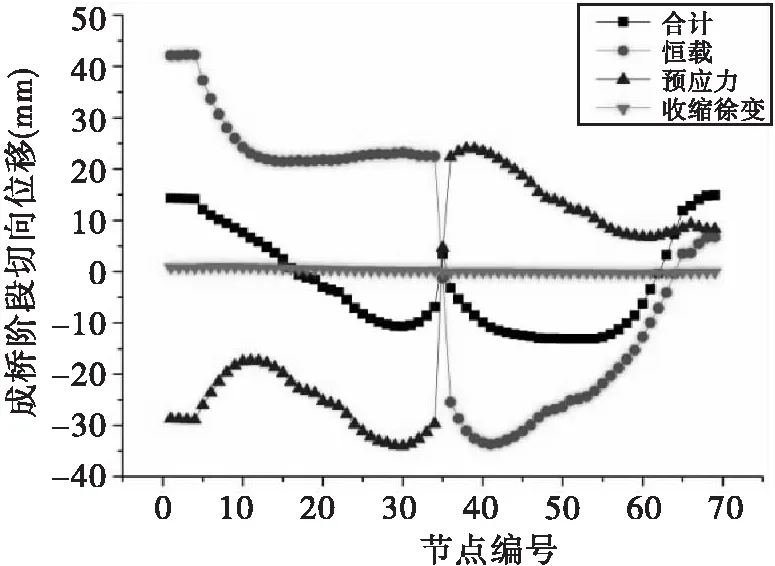
图10 成桥阶段主梁切向位移示意图

由图9～10可知，悬臂施工阶段，恒载对主梁切向位移影响最大，预应力次之，收缩徐变最小；除个别点外，全桥总体切向位移均为负值，最大切向位移(绝对值)达17.4mm。由悬臂施工阶段转换为成桥状态，主梁切向位移有所减小，最大切向位移为15.7mm。除个别节段外，恒载和预应力对切向位移影响效果相反，且均对切向位移有较大影响。

由以上分析可知，相比直线桥只考虑竖向变形，曲线桥变形复杂，须同时考虑竖向、径向和切向变形问题。

3 收缩徐变影响分析

不管是曲线连续刚构还是直线连续刚构，主梁持续下挠问题一直都是困扰工程界营运期的主要问题，根据以往工程经验，收缩徐变的影响不容忽视[9]。

混凝土收缩徐变为长期效应，随着时间的推移，其对结构影响将会越来越大。由于前文分析中所考虑的时间较短，无法准确把握收缩徐变对结构的影响，为此，有必要分析结构在考虑较长时间效应时，收缩徐变对主梁线形和内力的影响。

3.1 收缩徐变计算理论模型

《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTGD62-2004)采用欧洲国际混凝土委员会和国际预应力联合会推荐使用的CEB-FIP(1990)混凝土收缩徐变预测模型[10]。根据该模型，徐变系数的表达式为[11]：

φ(t,τ0)=φRHβ(fc)β(t0)βc(t-t0)

(1)

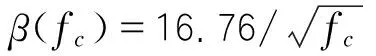
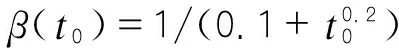
φRH=1+(1-RH/100)/0.1(0.2Ac/u)1/3取决于环境的参数。

徐变随应力持续时间的变化系数βc(t-t0)为：

(2)

βH取决于相对湿度和构件尺寸，按照式(3)计算：

(3)

CEB-FIB1990计算函数为：

εcs(t,ts)=εcs0βs(t-ts)

(4)

(5)

收缩应变随时间变化的系数βs(t-ts)为：

(6)

式中，fc——混凝土的圆柱体抗压强度；

Ac——构件的横截面面积；

u——构件与大气接触的截面周界长度。

3.2 收缩徐变计算结果

针对收缩徐变对主梁内力的影响，文献[12]研究结果表明：收缩徐变对梁体的轴力、径向剪力和竖向弯矩的影响绝对值较小，相对于恒载效应，收缩徐变对内力影响非常有限。限于篇幅，本文仅计算分析收缩徐变对曲线连续刚构线形的影响。

成桥不同年限的主梁竖向、径向、切向变形如图11～13所示。

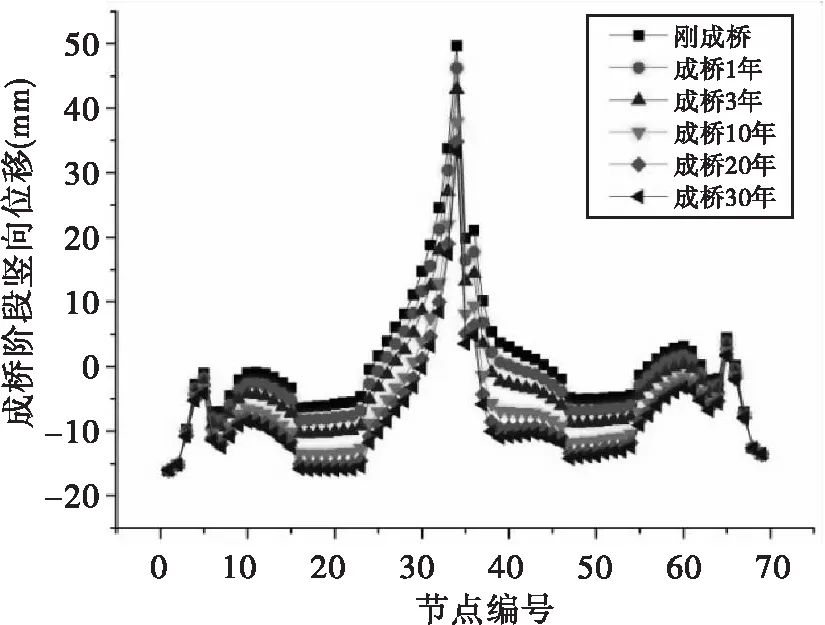
图11 收缩徐变对主梁竖向位移的影响示意图

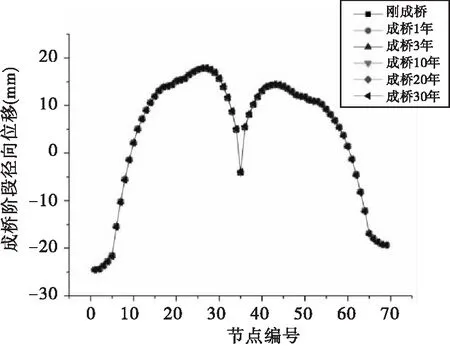
图12 收缩徐变对主梁径向位移的影响示意图

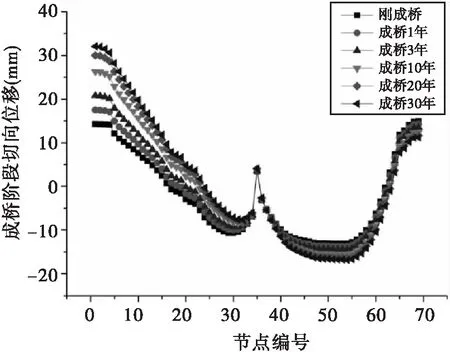
图13 收缩徐变对主梁切向位移的影响示意图

由图11可知，由于混凝土的收缩徐变效应，随着服役期的增长，主梁竖向下挠不断增大，30年间，主跨跨中位置变化最大，由刚成桥的19.8mm下挠至3.5mm。前3年发展速度较快，约完成主梁竖向位移变化的41%(以30年主梁竖向位移为终值)，成桥10年完成约72%，成桥20年完成90%。

由图12可知，收缩徐变对主梁径向位移影响很小，30年间，主梁径向位移同成桥初期相比，无明显变化。

由图13可知，混凝土收缩徐变对曲线刚构桥主梁的切向位移也有较大影响。服役30年间，边跨端部位置变化幅度最大，变化值为17.8mm。前3年约完成主梁切向位移变化的36%(以30年主梁切向位移为终值)，成桥10年完成约68%，成桥20年约完成88%。

根据以上分析结果，《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTGD62-2004)4.2.5中收缩徐变持续时间设置为10年的规定，对于曲线连续刚构桥是不安全的，设计时应考虑20年收缩徐变为宜。

4 结语

本文以某大跨PC曲线刚构桥为工程背景，建立空间有限元模型，在计算分析曲线连续刚构桥最大悬臂施工阶段和成桥阶段主梁恒载、预应力和混凝土收缩徐变对主梁线形和内力的影响的基础上，对收缩徐变对营运期主梁的影响进行分析，并得到以下结论：

(1)同直线桥相比，曲线连续刚构由于弯扭耦合作用的存在，内力状态更加复杂；主梁恒载对扭矩影响最大，预应力次之，收缩徐变最小。

(2)悬臂施工阶段和成桥阶段主梁同一截面相同高度横向应力相差较小，基本对称。

(3)曲线连续刚构桥施工、营运期间须考虑三个方向的变形。

(4)连续曲线箱梁桥中，收缩徐变对梁体的竖向位移和切向位移均有一定影响，且在前20年内影响较明显，按10年计算混凝土收缩徐变效应偏于不安全，应延长至20年。

[1]刘 云.预应力砼曲线连续刚构桥施工线形控制方法应用研究[D].重庆：重庆交通大学，2010.

[2]任茶仙，竺润祥.连续曲线箱梁预应力效应分析[J].工程力学，2000(4)：138-144.

[3]李新春，刘爱荣，张俊平.大跨曲线连续刚构桥预拱度的参数化研究[J].广州大学学报(自然科学版)，2009(3)：62-66.

[4]褚文涛，肖 奎，康凯乐，等.曲线连续刚构桥径向位移分析[J].华中科技大学学报(城市科学版)，2008(2)：96-99.

[5]郭 凡，杨永清，贾舒阳.高墩大跨预应力混凝土曲线连续刚构桥内力分析[J].四川建筑科学研究，2009(6)：35-37.

[6]郭 凡，杨永清，贾舒阳.高墩大跨预应力混凝土曲线连续刚构桥位移分析[J].四川建筑科学研究，2010(1)：15-17.

[7]杨孟刚，陈 庚.大跨度曲线刚构桥预应力设置对扭矩的影响[J].桥梁建设，2010(3)：15-18.

[8]崔颖波，龚德华，贾 山，等.预应力混凝土曲线连续刚构桥结构行为分析[J].四川建筑科学研究，2007(2)：43-44.

[9]邹立群.混凝土收缩徐变引起大跨度连续刚构桥长期下挠分析[D].北京：北京交通大学，2010.

[10]孟 江，赵宝俊，刘建梅.混凝土收缩徐变效应预测模型及影响因素[J].长安大学学报(自然科学版)，2013(2)：56-62.

[11]陈增顺.大跨轨道斜拉桥合理线形控制关键技术研究[D].重庆：重庆交通大学，2014.

[12]童智洋.混凝土收缩徐变对连续曲线箱梁桥的受力影响[J].铁道建筑，2010(6)：14-15.

Impact Analysis of Spatial Characteristics and Shrinkage & Creep of Large-span PC Curved Continuous Rigid Frame Bridge

XIN Jing-zhou，ZHOU Jian-ting，WANG Yu，YANG Mao

(School of Civil Engineering and Architecture，Chongqing Jiaotong University，Chongqing，400074)

In order to determine the spatial characteristics of curved continuous rigid frame bridge and its impact from shrinkage and creep，with a bridge as the engineering background，this article established the spatial finite element model by using the general bridge software Midas/Civil，analyzed the impact of main beam weight，prestressing force，and concrete creep on the internal force of main beam，the stress of critical sections and the deformation of main beam space at the largest cantilever stage and bridge completion stage of large-span PC continuous curve rigid frame bridge，while considering that the concrete shrinkage and creep is the long-term effect，it calculated the influence rules of shrinkage and creep on the curved continuous rigid frame as the growth of service period，and the research results can provide the reference for the design and construction of curved continuous rigid frame bridge.

Curved continuous rigid frame bridge；Bending moment；Torque；Stress；Displacement；Shrinkage and creep；Impact Analysis

EXPERTS

周建庭，教授、博士后，博士生导师，主要致力于桥梁安全状态监测、评估与旧危桥加固理论与技术的研究。主持国家973前期计划项目“大型在役桥梁结构系统时滞混沌动力行为研究及结构生命演化理论”及3项国家自然科学基金项目，承担其它国家、省部级项目17项；获国家科技进步二等奖2项、省部级科学技术奖13项；正式获得国家专利授权18项；发表学术论文193篇，出版著作7部。

辛景舟(1989—)，男，硕士研究生，研究方向：桥梁检测、评估、加固与健康监测。

西部交通建设科技项目(2011318223390)

U448.23

A

10.13282/j.cnki.wccst.2015.01.001

1673-4874(2015)01-0001-06

2014-12-05