A Double-layer Depth-averaged Boussinesq Model for Water Wave

LIU Zhong-bo,FANG Ke-zhao,LÜ Lin

(1.Transportation Management College,Dalian Maritime University,Dalian,116026,China;2.Water Science and Water Disaster Prevention and Control in Hunan Province Key Laboratory,Changsha University of Technology, Changsha 410114,China;3.State Key Laboratory of Coastal and Offshore Engineering,Dalian University of Technology,Dalian 116024,China)

A Double-layer Depth-averaged Boussinesq Model for Water Wave

LIU Zhong-bo1,2,3,FANG Ke-zhao2,3,LÜ Lin2

(1.Transportation Management College,Dalian Maritime University,Dalian,116026,China;2.Water Science and Water Disaster Prevention and Control in Hunan Province Key Laboratory,Changsha University of Technology, Changsha 410114,China;3.State Key Laboratory of Coastal and Offshore Engineering,Dalian University of Technology,Dalian 116024,China)

A double-layer depth-averaged Boussinesq-type model for wave propagation over an uneven bottom is derived.The governing equations are formulated in two depth-averaged velocities within each water layer and of the second-order fully nonlinearity.To improve the model properties,higher-order terms are introduced to momentum equations and theoretical analyses are made to investigate the linear dispersive and nonlinear properties.The optimized model equations show good dispersion property up to kh≈6 within 0.3%error,and the second nonlinear characteristics are optimized to kh≈6 within 10%error.Based on finite difference method and a composite fourth order Adams-Bashforth-Moulton time integration,one-dimensional equations are solved numerically on non-staggered grids.Regular wave evolution over a submerged breakwater is simulated and the computational results are compared with the experimental data,the good agreements are found.

Double-layer Boussinesq equations;dispersive property;nonlinear property

0 Introduction

Boussinesq-type equations have been proven to be powerful coastal wave models because they have both dispersive and nonlinear properties,as well as acceptable computational cost due to reducing three-dimensional problem to two-dimensional ones.The research on Boussinesq theory is mainly triggered by improving the capabilities of linear and nonlinear properties in deep water,comprehensive review of the Boussinesq type models is referred to Kirby and Madsen and Fuhrman[1-2].

Early research mainly focused on improving the linear dispersion of classical Boussinesq equations presented by Peregrine to deep water[3].With an improved dispersion to non-dimensional water depth kh≈3.14,most of these Boussinesq models only included the weakly non-linear terms(e.g.,Madsen et al(1991)[4];Nwogu(1993)[5];Beji and Nadaoka(1996)[6]).Subsequently,the nonlinear property was found to play a key role in accurate predicting water waves and great efforts have been made to develop the‘full nonlinear’Boussinesq model(Wei,et al(1995)[7];Madsen and Schäffer(1998)[8];Zou(1999)[9];Gobbi et al(1999)[10];Agnon et al (1999)[11]).After 2000,some novel Boussinesq models emerged with high accuracy in both linear and nonlinear properties(e.g.,Madsen et al(2002)[12];Lynett and Liu(2004)[13];Chazel et al(2009)[14]).Notably the equations derived by Madsen et al(2002)[12]showed an excellent linear property up to kh≈25-40 and nonlinear property up to kh≈25-30.This model however included more equations than conventional Boussinesq models and contained fifth-order derivatives,thus resulting in a very complex numerical discretization as well as expensive computational time.To avoid solving the fifth-order derivatives in Boussinesq models,Zhang and Li[17]and Lynett and Liu[18]presented two-layer Boussinesq models for water waves.These kinds of models included one more momentum equations compared with the conventional Boussinesq models and the highest derivative is 3.And the models proposed by Zhang and Li[17]and Lynett and Liu[18]were expressed in terms of two velocities,which defined at different water column, and the former one incorporated weakly nonlinear terms while the latter was a full nonlinear model.In this study,a new set of double-layer depth-averaged Boussinesq equations is derived starting from the Laplace equations.Theoretical analyses as well as numerical experiments were performed.

1 Theoretical derivation of a double-layer depth-averaged Boussinesq model

1.1 Scaling and governing equations

A Cartesian coordinate system is adopted with the x-and y-axes located on the still water plane(SWL)and the z-axis pointing vertically upwards as shown in Fig.1, whereis the surface elevation measured fromare the upper and lower water depths,respectively;and h=h1+h2is the still water depth.Under the assumption of irrotational motion of fluid,andare utilized to represent the velocity potential in the upper and lower water layers,respectively.

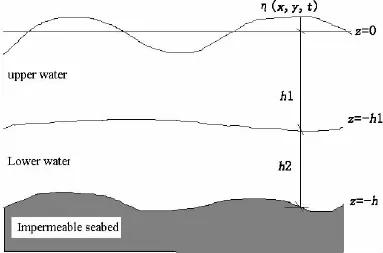
Fig.1 The sketch of wave propagation over impermeable seabed

The variables are rescaled to the non-dimensional ones as

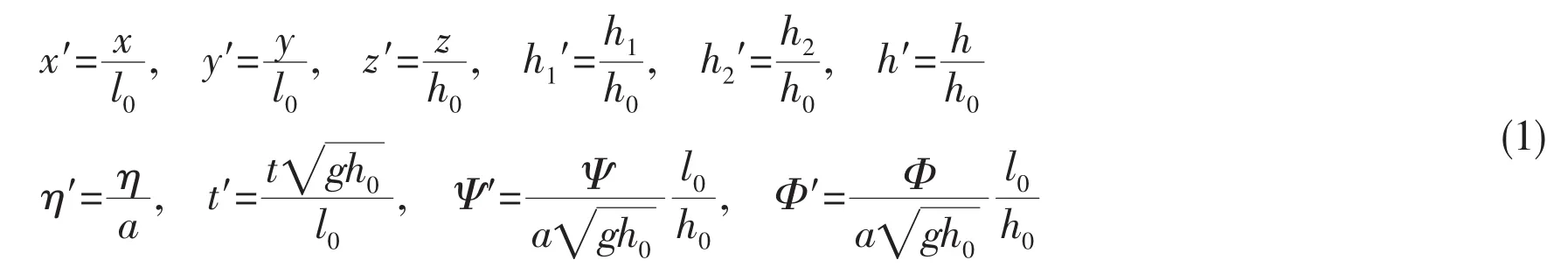
where the prime denotes non-dimensional variables;and a,l0,and h0denote the characteristic wave amplitude,wave length,and water depth,respectively.

Introducing two small parameters ε and μ as the classical measures of nonlinearity and frequency dispersion as follows,

and the governing equations,boundary conditions,and matching conditions at the interface for the irrotational wave problem shown in Fig.1 are obtained(omitting the primes for clarity):

1.2 The expansion of velocity potentials

The most significant advantage of the Boussinesq model is that it can decrease a complicated three-dimensional problem into a two-dimensional one by assuming a specific vertical distribution of velocity.To achieve this,we choose the expansions forand Ψ）as:

Substituting the expression(10)into Eqs.(3)and(7)and then applying the assumption of▽h=leads to successive expressions,and after rearrangement,can be written as:

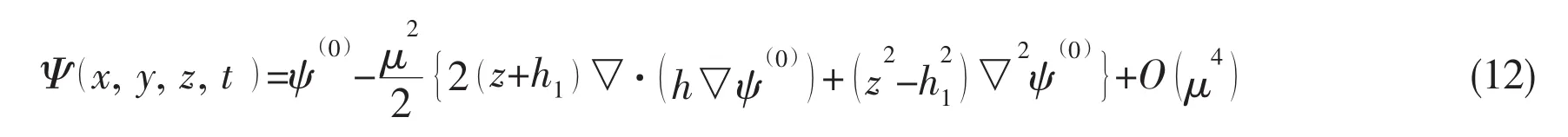
Similarly,after the expression(11)is substituted into Eqs.(4)and(8),we can have the expressions forwhich is written as

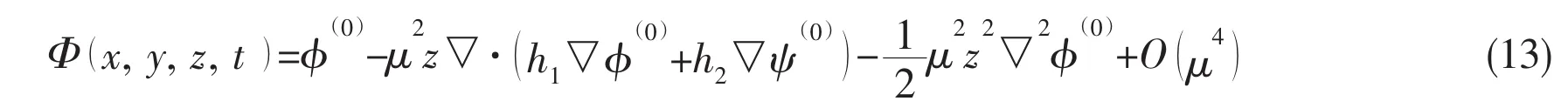
Eqs.(12)and(13)are truncated at）to ensure that the highest spatial derivative in the equations is 3,which will be convenient for numerical discretization.

1.3 Equations in terms of the velocities at the still water level u0and interfacial water depth u10

Inserting the expressions(12)and(13)into Eq.(5),we can obtain

Applying horizontal gradient operator▽to Eq.(14),we obtain

Similarly,we can obtain the second momentum equations expressed in terms of two velocities at the still water level and interfacial water depth as:

The continuity equation is

where

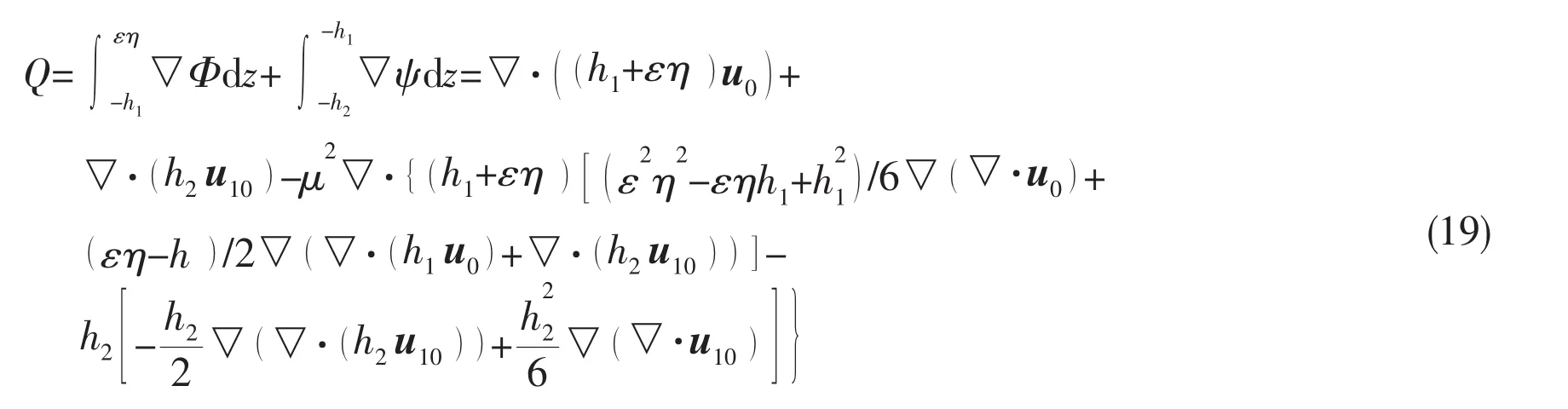
The combination of Eqs.(15),(16)and(18)represents a complete system of higher-order Boussinesq equations truncated atand retains all second nonlinear terms.The model has a poor dispersion property because no second-order dispersion terms are involved in the governing equation for u0(see Eq.(16)).However,this model serves as a basis for deriving the following depth-averaged model in the following sections.

1.4 Equations formulated in terms of depth-averaged velocities

The depth-averaged velocities along the upper and lower water columns are defined as:

Inserting the expressions(12)and(13)in Eqs.(20)and(21)leads to

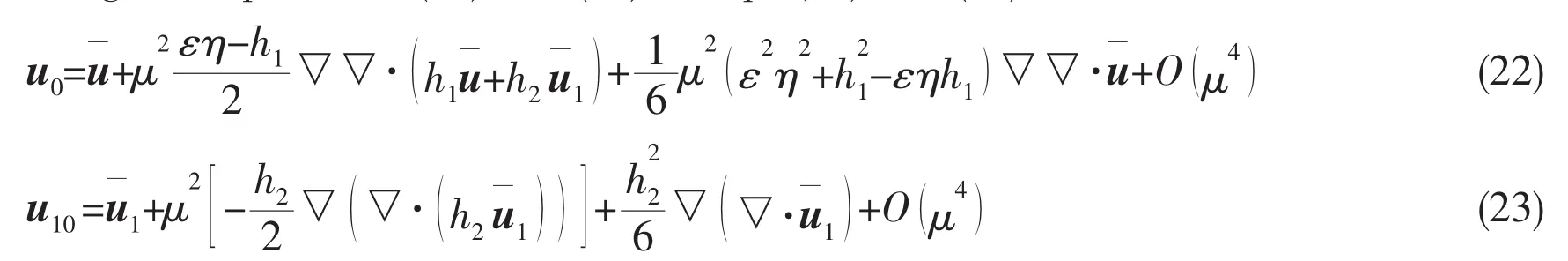
Substituting the the expressions(22)and(23)into Eqs.(15),(16)and(18),we finally obtain a double-layer depth-averaged Boussinesq model,which is written as:

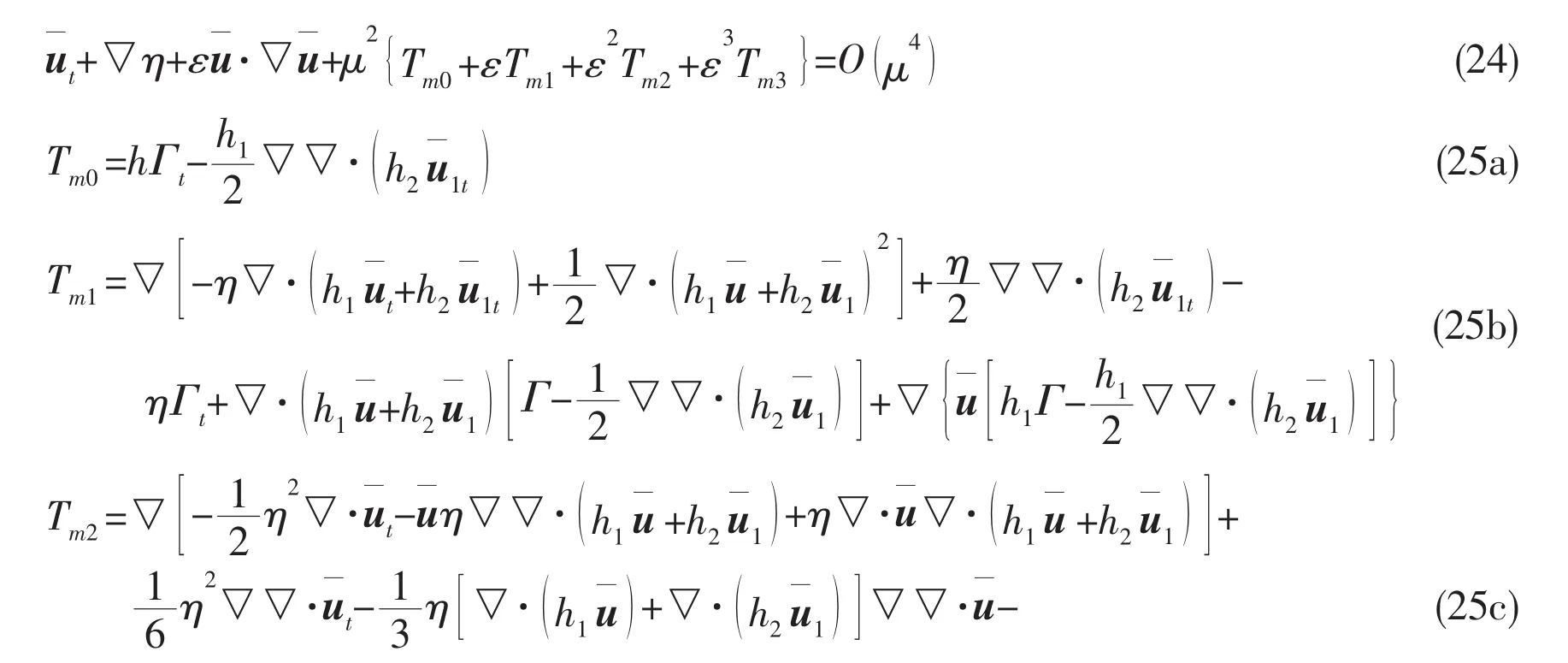
The combination of Eqs.(24),(26),and(28)represents a set of higher-order Boussinesq equations in terms of depth-averaged velocities and surface elevation(hereafter we call it Model I).Neglecting Eq.(26)and the terms related to depth-averaged velocity along the lower water column in Eqs.(24)and(28),the model is simplified to the classical Boussinesq model with the inclusion of the second-order nonlinear terms[3].

1.5 The enhanced Boussinesq model with better linear and nonlinear properties

The method suggested by Madsen and Schäffer[8]and Liu et al[19]is modified and applied to further extend models’application range.The resulting expressions are given as:

where β1and β2are dispersion coefficients,γ1and γ2are nonlinear coefficients.

The related research demonstrated that the introducing additional nonlinear terms played an important role in improving the nonlinear performance[19].Inserting Eqs.(29)and(30)into the left sides of Eqs.(24)and(26),respectively,creates an enhanced double-layer Boussinesq model,hereafter we call it Model II.Model II shares some similarity with Lynett and Liu’s model[18]:The highest spatial derivative is 3 and both of the models are accurate to secondorder.And there are three apparent differences:(1)The continuity equation in Model II is accurate,while it is only accurate to μ2in Lynett and Liu’s model;(2)The velocities are two depth-averaged ones in Model II while the velocities are defined at two arbitrary water columns in Lynett and Liu’s model.

1.6 Theoretical analysis of equations

Stoke-type Fourier analysis is conducted to obtain the dispersion and nonlinear second harmonic embodied in the Boussinesq equations.The main procedures of the analytical analysis for Model II are outlined in this section for clarity.The solutions to the Boussinesq equations are assumed to have the following form[8]:

where θ=ωt-kx,ω is frequency and k is wave number,and the subscripts 1 and 2 denote the amplitude of the first-and second-order solutions,respectively.

Inserting Eqs.(31),(32)and(33)into Model II for a constant water depth case and collecting the terms,we can obtain the first-order solution that corresponding to dispersion expression,and the second-order solution for nonlinear second harmonic amplitude,see Ref.[8] for detailed process.

1.6.1 Phase celerity

There coefficients involved in Model II are r=h1/h2,β1and β2.For general case,we take r＝0.5.For kh belongs to(0,6)，the other two coefficients are determined from minimizing the following integral error:

Thus we have β1=-0.056,β2=-0.113,and the non-dimensional phase celerity are shown in Fig.2.To well understand the importance of two coefficients,the results of Model I(β1=0,β2= 0)are plotted in this figure,and the results of Zou and Fang’s model(hereafter we call it as BouN4D4)are also given for comparisons[16].In Fig.2,we can see that the maximum error is 5%for Model I covering the water depth kh from 0 to 2.33,while the maximum error is 0.3% for Model II and 1.6%for BouN4D4 within the(0,6)range,thus the dispersion accuracy of Model II is much higher than that of Model I,this demonstrates the importance of the two coefficients.

1.6.2 Second-order harmonic amplitude

In present paper,γ1=4.9 and γ2=2.9 are determined to obtain a very accurate nonlinear property,and the results of second-order harmonics amplitude are shown in Fig.3.In Fig.3, the optimized nonlinear property is far better than the original model(γ1=0,γ2=0).In thisfigure,the second-order nonlinear property of BouN4D4 is also shown.Within maximum error 10%,the applicable maximum water depth is 6 for Model II,while it is 1.8 for BouN4D4.

Fig.2 Dimensionless wave phase celerity

Fig.3 Ratio of second harmonic a/aStokes22

2 Numerical model and its verification

1D numerical model is established,and this model can be solved by a similar numerical scheme to that of Kirby et al and Liu et al[20-21],which has second-order accuracy in spatial and temporal discretization with certain modifications.Only the first derivatives adopt five-point formula while the second-and third-derivatives use second-order difference accuracy.A composite fourth-order predictor-corrector Adams-Bashforth-Moulton integration scheme is adopted in the model to perform time marching.To decrease the wave reflection from the boundaries,the internal wave generation method in Gobbi et al(2000)[10]is used and two sponge boundary layers are set at left and right boundaries.

To validate the present model,the numerical simulations are carried out upon wave evo-lution over a submerged trapezoid breakwater.We illustrate the wave process here:before the wave propagates on the flat part of the breakwater,all the fundamental wave and higher-order harmonic waves are bounded together,they travel at the same speed.When they go down the breakwater,water depth becomes deeper and nonlinear coupling of higher harmonics with the fundamental wave becomes progressively weaker at the leeside of the bar.Therefore,each Fourier component is released as a free wave and travels at its own speed,thus resulting in a fairly complicated process.Computing this wave evolution process requires high accuracy in linear and nonlinear property of a model.This process has been widely used as a benchmark test to validate Boussinesq models and other type numerical models.In present paper,we choose the Luth’s experiment to investigate our models[22],and the experiment layout is shown in Fig.4.

Fig.4 The experimental setup of Luth et al.All dimensions are in(m)

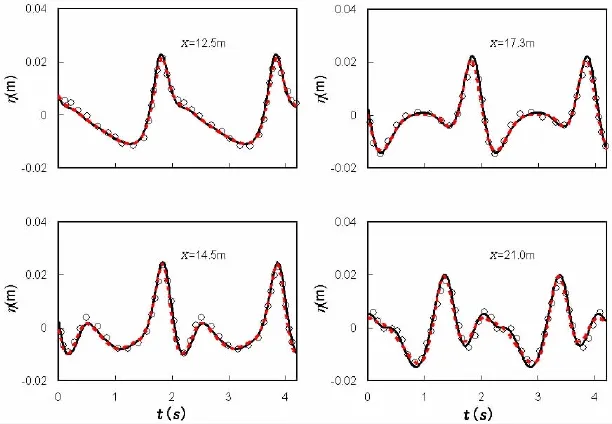
Fig.5 Comparisons of computed surface elevation with experimental data for case(a).Circle dot is experimental data,solid line is Model II,and dashed line is BouN4D4

In case(a),wave period is T=2.02 s and wave height is 0.02(kh=0.67),and wave period is 1.01 s and wave height is 0.041 m(kh=1.69)in case(b).Regular wave in a 50 m-long nu-merical flume is internally generated,and the source line is set at x=10 m.The time and spatial size for the simulation are 0.01 s and 0.02 m,respectively in the numerical simulations. The computed surface elevations are shown in Figs.5 and 6.To make comparisons,the results of BouN4D4 are also plotted here[16].As shown in these two figures,the computed results using Model II or BouN4D4 are well in agreements with the experimental data,and the agreement of Model II is a little better than BouN4D4 at some transections,this might attribute to a bit higher accuracy in dispersion and nonlinear accuracy of Model II.Furthermore,Fourier analysis is applied to the experimental and numerical results to obtain the higher-order harmonics amplitude along the flume,and the results are shown in Figs.7 and 8.Overall,the computed amplitudes of higher-order harmonics by Model II agree well with the experimental data.

Fig.6 Comparisons of computed surface elevation with experimental data for case(b).Circle dot is experimental data,solid line is Model II,and dashed line is BouN4D4

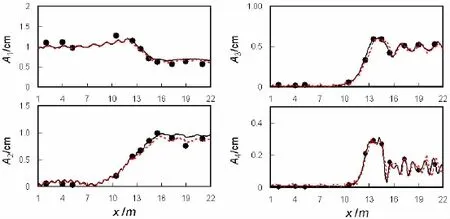
Fig.7 Comparisons of computed harmonics amplitudes and experimental data for case(a).Circle dot is experimental data,solid line is Model II,and dashed line is BouN4D4

Fig.8 Comparisons of computed harmonics amplitudes and experimental data for case(b).Circle dot is experimental data,solid line is Model II,and dashed line is BouN4D4

3 Conclusions

A set of double-layer Boussinesq model is derived in present paper.The Boussinesq model is expressed in terms of two depth-averaged velocities and it is accurate to second-order. Higher-order linear and nonlinear terms are introduced to improve the accuracy in both linear and nonlinear properties.Numerical model is established and the numerical model is applied to simulate wave evolution over a submerged trapezoid breakwater.

Through the research,we have two main conclusions:(1)The dispersion and nonlinear accuracy of Model II are very high,it can be applicable to maximum water depth 6.0 within 0.3%and 10%errors in the viewpoint of dispersion and nonlinear properties.Theoretically speaking,Model II has an advantage over BouN4D4.(2)The numerical result shows that Model II can be as good as BouN4D4 in describing the wave evolution over a trapezoid breakwater, and even more precise in some Gauge locations.

The one-dimensional numerical model for surf zone dynamic is ongoing and further research will concern about wave breaking in surf zone and moving shoreline in swash zone, and this will be done in near future.

Acknowledgements

This research was supported by the National Natural Science Foundation of China(Grant No.51379026 and 51309040);The National Basic Research Program of China(973 Program) (Grant No.2013CB036101);Key Laboratory of Water-Sediment Sciences and Water Disaster Prevention of Hunan Province(Grant No.2015SS01);The Fundamental Research Funds for the Central Universities(Grant No.3132015071).

[1]Kirby J T.Boussinesq models and applications to nearshore wave propagation,surfzone processes and wave-induced currents[M].Advances in Coastal Engineering,New York:Elsevier Science,2003:1-41.

[2]Madsen P A,Fuhrman D R.High-order Boussinesq-type modeling of nonlinear wave phenomena in deep and shallow water[M].Advances in Numerical Simulation of Nonlinear Water Waves,Singapore:World Scientific Publishing Co.Pte. Ltd.,2010:245-285.

[3]Peregrine D H.Long waves on a beach[J].Journal of Fluid Mechanics,1967,27(4):815-827.

[4]Madsen P A,Murray R,Sørensen O R.A new form of the Boussinesq equations with improved linear dispersion characteristics,Part 1[J].Coastal Engineering,1991,15(4):371-388.

[5]Nwogu O.Alternative from of Boussinesq equations for nearshore wave propagation[J].Journal of Waterway,Port,Coastal, and Ocean Engineering,1993,119(6):618-638.

[6]Beji S,Nadaoka K.A formal derivation and numerical model of the improved boussinesq equations for varying depth[J]. Ocean Engineering,1996,23(8):691-704.

[7]Wei G,Kirby J T,Grilli S T,et al.A fully nonlinear Boussinesq model for surface waves.Part 1.Highly nonlinear unsteady waves[J].Journal of Fluid Mechanics,1995,294(13):71-92.

[8]Madsen P A,Schaffer H A.Higher-order Boussinesq-type equations for surface gravity waves:Derivation and analysis[J]. Philosophical Transactions of the Royal Society of London.Series A,1998,356(1749):3123-3184.

[9]Zou Z L.Higher order Boussinesq equations[J].Ocean Engineering,1999,26(5):767-792.

[10]Gobbi M F,Kirby J T.Wave evolution over submerged sills:Tests of a high-order Boussinesq model[J].Coastal Engineering,1999,37:57-96.

[11]Agnon Y,Madsen P A,Schaffer H A.A new approach to higher order Boussinesq model[J].Journal of Fluid Mechanics, 1999,399(1):319-333.

[12]Madsen P A,Bingham H B,Schaffer H A.Boussinesq-type formulations for fully nonlinear and extremely dispersive water waves:Derivation and analysis[J].Philosophical Transactions of the Royal Society of London.Series A,2003,459 (2033):1075-1104.

[13]Lynett P,Liu P L-F.Linear analysis of the multi-layer model[J].Coastal Engineering,2004,51(6):439-454.

[14]Chazel F,Benoit M,Em A,Piperno S.A double-layer Boussinesq-type model for highly nonlinear and dispersive waves [J].Proceedings of the Royal Society of London,2009,465:2319-2346.

[15]Fuhrman D R,Madsen P A,Bingham H B.A numerical study of crescent waves[J].Journal of Fluid Mechanics,2004, 513:309-341.

[16]Zou Z L,Fang K Z.Alternative forms of higher order Boussinesq equations:Derivations and validations[J].Coastal Engineering,2008,55(6):506-521.

[17]Zhang Y G,Li Y C.Alternative form of the Boussinesq equations with improved linear dispersion characteristics[J].Acta Mechanica Sinica,1997,29(2):142-150.

[18]Lynett P,Liu liu P L-F.A two-layer approach to wave modeling[J].Philosophical Transactions of the Royal Society of London.Series A,2004,460(2049):2637-2669.

[19]Liu Z B,Fang K Z,Zou Z L.Boussinesq wave equations with full nonlinear characteristics at order O μ2（）[J].Journal of Harbin Engineering University,2012,33(5):556-561.

[20]Kirby J T Kirby,Wei G,Chen Q,et al.FUNWAVE 1.0 Fully nonlinear Boussinesq wave model documentation and user’s manual[R].CACR-98-06,University of Delaware,Newark,US,1998.

[21]Liu Z B,Sun Z C,Fang K Z.Mathematical model for wave propagation over a permeable seabed and its numerical validation[J].Journal of Dalian University of Technology,2013,53(3):417-422.(in Chinese)

[22]Luth H R,Klopman G,Kitou N.Kinematics of waves breaking partially on an offshore bar,LDV measurements of waves with and without a net onshore current[R].Report H-1573,Delft Hydraulics,1994:40.

双层Boussinesq水波方程

刘忠波1，2，3，房克照2，3，吕 林

（1.大连海事大学 交通运输管理学院，辽宁 大连 116026；2.长沙理工大学 水沙科学与水灾害防治湖南省重点实验室，长沙 410076；3.大连理工大学 海岸和近海工程国家重点实验室，辽宁 大连116023）

从Laplace方程出发，推导了一组适应于波浪在非平整地形上传播的双层Boussinesq水波方程，方程以双层水深积分平均速度表达且具有二阶全非线性特征。通过在动量方程中引入高阶色散项和非线性项进一步提高了方程的色散性和非线性性能。常水深情况下，分析了方程的色散关系和二阶波幅传递函数，并与Stokes解析解进行了比较。结果表明，在0.3%误差下方程可适用水深达kh≈6，在此水深范围内二阶波幅传递函数误差在10%以内。在非交错网格下，建立了基于有限差分方法和混合4阶Adams-Bashforth-Moulton时间积分格式的一维数值模型，模拟了波浪在潜堤上的传播变形，并与实验结果进行了对比，吻合程度较好。

双层Boussinesq方程；色散性；非线性

O353.2

:A

刘忠波（1976-），男，大连海事大学交通运输管理学院副教授；

O353.2

:A

10.3969/j.issn.1007-7294.2015.09.005

1007-7294（2015）09-1072-13

房克照（1980-），男，大连理工大学海岸和近海工程国家重点实验室讲师；

吕 林（1976-），男，大连理工大学海岸和近海工程国家重点实验室副教授。

Received date：2015-03-18

Foundation item:Supported by the National Natural Science Foundation of China(Grant No.51379026 and 51309040); The National Basic Research Program of China(973 Program)(Grant No.2013CB036101);Key Laboratory of Water-Sediment Sciences and Water Disaster Prevention of Hunan Province(Grant No.2015SS01); The Fundamental Research Funds for the Central Universities(Grant No.3132015071)

Biography：LIU Zhong-bo(1976-),male,lecturer,E-mail:zhongbo_liu1976@163.com; FANG Ke-zhao(1980-),male,lecturer.