线性涡流制动的制动力特性仿真分析*

李 辉, 詹普亚, 丁福焰, 孙立增

(1 中国铁道科学研究院 机车车辆研究所， 北京100081；2 北京能奥科技发展有限公司， 北京100011)

线性涡流制动的制动力特性仿真分析*

李 辉1, 詹普亚2, 丁福焰1, 孙立增2

(1 中国铁道科学研究院 机车车辆研究所， 北京100081；2 北京能奥科技发展有限公司， 北京100011)

以试验用线性涡流制动电磁铁为研究对象，从能量转化角度推导涡流制动力的计算式，建立简化的二维静态电磁场模型，并借助于有限元分析软件进行计算，得出励磁电流、工作气隙和运动速度等参数对涡流电磁铁制动力的影响，为涡流制动电磁铁的设计提供参考。

涡流制动； 制动力特性； 有限元仿真； 高速列车

线性涡流制动不依靠轮轨之间的黏着，在高速区段可发挥较大的制动力，有效缩短制动距离，减少制动盘和闸片的磨耗，并且具有无机械磨损、无气味、无噪声等特点，是高速列车复合制动方式中一种重要的辅助制动方式。目前，线性涡流制动装置已在德国ICE3高速动车组上批量应用[1-2]。

制动力特性研究是涡流制动装置研制的重要内容。我国从20世纪90年代开始进行了一些理论和试验研究，例如朱仙福等采用有限元方法进行了计算和分析[3-4]，郭其一、张逸成等分别利用解析法进行了推导和计算[5-6]，应之丁等采用试验方法进行了研究[7]，这些工作对认识和描述涡流制动力的变化规律起到了积极的作用。

为了研制1∶1试验用线性涡流制动电磁铁，对涡流制动的制动力特性进行了研究。涡流制动时，制动电磁铁、气隙和钢轨间形成三维非线性动态电磁场，建模和求解非常困难。采用二维静态电磁场模型对问题进行简化，推导涡流制动力的计算公式，并对励磁电流、工作气隙和速度的影响进行分析，试图通过简化的方法为电磁铁的设计和研制提供依据。

1 涡流制动原理及制动力计算方法

1.1 涡流制动原理

线性(轨道)涡流制动器的核心部分主要由磁轭、磁极和线圈组成，电磁铁沿钢轨纵向呈N、S极交替分布，并与钢轨顶面保持一定的气隙，其中的一对磁极如图1所示[8]。线性涡流制动基本原理为：当列车静止(v= 0)时，由励磁线圈产生的磁场是对称、恒定的，制动电磁铁与钢轨之间只有垂向吸力FA。当列车运行(v> 0)

时，穿越钢轨表面的磁通交替变化，且钢轨切割磁力线。由法拉第电磁感应定律[9]可知，钢轨内会感应出阻碍磁通变化的电涡流，由电涡流形成的磁场使原磁场发生畸变，形成切向电磁力(洛伦兹力)，即涡流制动力。从能量角度来说，制动过程中由于电磁作用而在钢轨表层感应出电涡流，则列车的动能通过电涡流转化为热能，再通过周围的空气耗散。

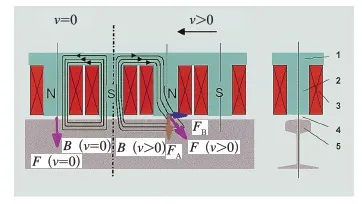
1-磁轭；2-磁极；3-线圈；4-气隙；5-钢轨。图1 线性涡流制动原理图

1.2 涡流制动力计算方法

线性涡流制动的问题其实是涡流电磁铁、气隙和钢轨形成的一个变边界的三维交变非线性电磁场，并且磁场的分布状态与相对运动速度有关，钢轨表层存在磁饱和集肤效应，这些因素会导致动态求解整个空间磁场变得异常复杂，难度较大。

文献[10]基于磁路欧姆定律、电涡流及电涡流功率的理想模型微积分以及涡流制动能量转化过程，计算得到了涡流制动装置一对磁极所产生的电涡流功率与励磁电流、气隙、运动速度、钢轨电导率、电磁铁磁导率的关系：

(1)

式中，P为单对磁极所产生的电涡流功率；lt、lc、lg、l0分别为磁通回路在磁极、磁轭、钢轨和气隙中的长度；μr和μ分别为电磁铁相对磁导率和空气磁导率；τ为相邻异性南北磁极的间距；σ为钢轨电导率；δ为集肤深度；n为励磁线圈匝数；I0为励磁电流；D为电涡流区域等效直径；v为相对运动速度；ke代表涡流电流去磁系数。

采取用静态电磁场模型来替代动态电磁场模型，根据涡流制动时能量转化原理计算涡流制动力，分析过程如下：

在涡流制动时，考虑涡流电磁铁经过钢轨上一固定截面(面积S)过程中，由于涡流电磁铁沿钢轨纵向的长度相对很小，前后磁极经过该截面时的速度近似相等，因此可以认为：该固定截面的磁感应强度幅值(B)可看做近似不变，而穿过该截面的磁通会呈现周期性变化，其在一个周期内的变化规律如下：

为了研究方便，假定穿过钢轨截面磁通量的这种周期性循环为余弦函数，涡流制动t时刻穿过钢轨截面的磁通量Φ可按下式计算：

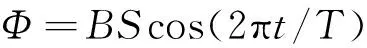
(2)

式中T为变化周期。

因此,运动状态下穿过钢轨截面磁通量的变化可近似等效为涡流电磁铁与钢轨相对静止时，线圈励磁电流按照余弦函数变化的静态磁场模型。包含k对磁极的涡流电磁铁在钢轨中所产生的电涡流功率在静态电磁场模型下可以表述为：

(3)

根据文献[6]，涡流产生的热功率就是制动功率。由此可得：

(4)

Wouterse研究了不同速度下的磁场，发现3个重要现象[11]：

(1) 在低速时，磁场与静止状态磁场比较变化很小；

(2) 在出现最大制动力的临界速度附近，平均磁感应强度明显小于初始磁感应强度；

(3) 在更高速度时，磁感应强度的大小趋向于进一步的衰减。

因此，Wouterse提出了高速时制动力F′的计算模型为：

(5)

式中v为运动速度；vk为临界速度，即制动力最大时的速度。但在划分高速和低速区判断临界速度vk时存在着困难，解决的办法一般是利用试验结果对高速区计算公式进行修正。

2 涡流仿真结果

根据1∶1试验用涡流制动电磁铁基本参数，在有限元软件ANSYS中建立了涡流制动分析模型，如图2所示。取磁极对数k= 6，磁轭长度lc=1 800 mm，磁极间距τ=150 mm，临界速度vk=100 km/h。

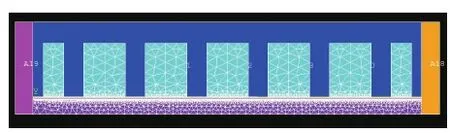
图2 涡流电磁铁有限元分析模型

利用ANSYS编写分析程序，输入磁轭、磁极和钢轨材料的实测B-H特性，励磁线圈匝数和电流，钢轨电导率等参数，可得到试验用涡流制动电磁铁在不同气隙、不同励磁电流参数下产生的电涡流功率。由式(4)和式(5)联合求解可以得到低速和高速区的制动力。

2.1 制动力、吸引力与励磁电流关系

图3为涡流电磁铁(工作气隙为6 mm)在励磁电流分别为120,160和200 A时的制动力随运动速度的变化曲线。从仿真结果可以看出：在励磁电流一定时，涡流制动力在低速区随着速度的增加而显著的增大，速度到达一定值(临界速度)时制动力存在最大值，速度继续增大时，制动力有一定的下降趋势，在高速区表现出良好的制动特性。

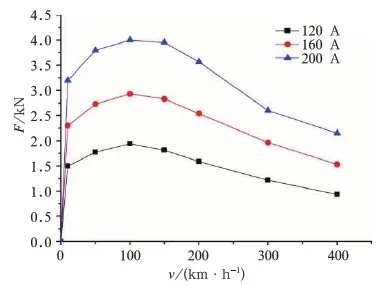
图3 不同励磁电流下制动力与速度的关系

随着励磁电流的增大，相应的制动力也在提高。当励磁电流I=120 A时，150 km/h速度时制动力F=1.86 kN；当励磁电流为I=200 A时，150 km/h速度时制动力F=3.9 kN。当电流增加75%时，制动力增加109%。因此，对于本文研究的试验用涡流电磁铁而言，在其他参数不变的情况下，可近似看做制动力与电流存在线性比例关系。

图4为涡流电磁铁在励磁电流分别为120,160和200 A时与钢轨间吸引力随运动速度的变化曲线。涡流产生的吸引力随着速度的提高下降趋势明显，当运动速度大于100 km/h后，高速区涡流产生的吸引力较小，可明显改善涡流电磁铁横梁的受力状态，而在低速区时吸引力较大。因此，涡流制动非常适合列车在高速时的制动，低速时考虑结构件的受力则可以撤除。

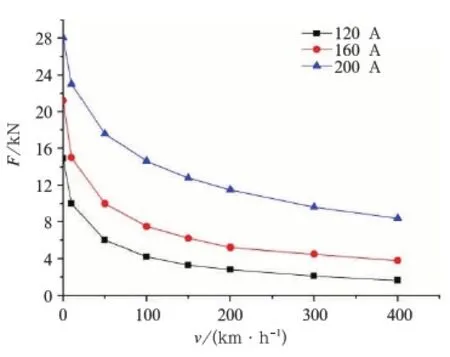
图4 不同励磁电流下吸引力与速度的关系

2.2 制动力、吸引力与工作气隙关系

给定励磁电流I=200 A前提条件下，分别设定工作气隙为4、6和9 mm 3组值，得到3种气隙条件下制动力和吸引力与速度的关系，分别如图5、图6所示。从图中可以看出，随着工作气隙的减小，制动力和吸引力均有明显增大趋势。从磁路欧姆定律角度考虑，磁场强度随着磁阻的增大而减小，这点很容易理解。

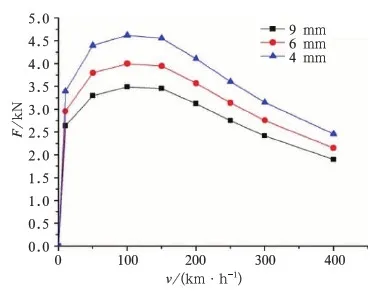
图5 不同气隙下制动力与速度的关系

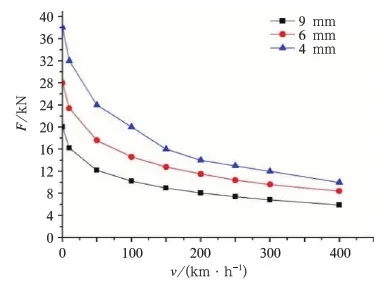
图6 不同气隙下吸引力与速度的关系

2.3 仿真结果分析

涡流制动力在低速区随速度的提高而增大，在高速区随速度的提高而下降，在临界速度(约为100 km/h)时达到最大，从制动过程中的电磁机理[12]考虑，存在以上趋势的原因主要有：

(1) 磁场方向变化频率随着速度的提高而增大，很快磁路达到饱和；

(2) 磁势与磁通的相位差随速度的提高而越来越大，因而沿着磁路各段的方向磁通密度既不同相也不同值；

(3) 主磁通在钢轨头内穿透的深度随速度的提高而减小，磁路的有效截面积变小，磁阻增大；

(4) 钢轨反复磁化，磁滞也因速度的提高而越来越厉害

(5) 高速时钢轨中产生的电涡流对磁极励磁线圈产生感抗，导致线圈等效电阻变大，线圈电流变小，磁势变小，涡流制动力变小。

所有以上因素都会导致工作气隙的有效磁通随着速度的提高而减小。

3 结束语

从能量转化角度研究了涡流制动过程的制动力特性，将三维动态电磁场模型的计算转化为二维静态分析模型，并借助ANSYS有限元软件对影响制动力的主要因素——励磁电流、工作气隙和运动速度进行了分析，得出不同设计参数下的制动力、吸引力计算结果，可供涡流制动电磁铁设计和研制参考。由于在模型简化过程中，未考虑磁场的空间分布，且忽略了一些因素如边缘效应、温度变化等的影响，因此计算结果存在一定的误差，有待进一步深入研究或试验验证。

致 谢:同济大学应之丁教授在本文仿真数据的分析处理方面给予了宝贵的协助和热心指导，谨在此深表谢意。

[1] Prem, J.等[德]. 大功率常用制动系统——ICE3的涡流制动(一)[J]，变流技术与电力牵引，2005, (1): 7-12.

[2] Prem, J.等[德]. 大功率常用制动系统——ICE3的涡流制动(二)[J]，变流技术与电力牵引，2005, (3): 15-22.

[3] 朱仙福. 线性涡流制动电磁分析[J]，上海铁道学院学报，1994, 15(2): 55-63.

[4] 朱仙福，张秀荣. 高速列车轨道涡流制动的制动力分析与计算[J]，上海铁道大学学报(自然科学版), 1996, 17(4): 1-8.

[5] 郭其一，陈 鹏，骆廷勇，李维刚. 基于解析法的涡流制动电磁机理研究[J]，机车电传动，2006, (1): 30-32.

[6] 张逸成，沈玉琢，庞乾麟,等.旋转涡流制动器电磁机构的设计研究[J].铁道学报，1998(6):22-27.

[7] 应之丁，夏寅荪，邵丙衡. 轨道涡流制动试验与研究[J]，上海铁道大学学报，1999, 20(6): 93-97.

[8] 丁福焰，吕宝佳，顾磊磊. 高速列车涡流制动技术综述[J]，铁道机车车辆，2012, 32(6): 1-4, 20.

[9] 冯慈璋，马西奎. 工程电磁场导论[M]. 第1版. 北京：高等教育出版社，2000：146-148.

[10] 郭其一，黄世泽，吴伟银，胡景泰. 磁浮列车涡流制动热效应研究[J].铁道学报，2012,34(1)：29-33.

[11] 应之丁，林建平. 列车涡流制动机理及制动力矩模型[M]. 第1版. 上海：同济大学出版社，2014：73-76.

[12] 智廉清，吴培元，林台平，孙福祥. 近代铁道制动技术[M]. 北京:中国铁道出版社，1983.

Simulating Analysis of Braking Force Characteristics of Linear Eddy Current Brake

LIHui1,ZHANPuya2,DINGFuyan1,SUNLizeng2

(1 Locomotive and Car Research Institute, China Academy of Railway Sciences. Beijing 100081, China;2 Beijing Neng-ao Technology Development Co., Ltd. Beijing 100011, China)

This article takes a linear eddy-current brake magnet used in test for the research object. It derives equations of eddy current braking force from energy conversion. It builds a simplyfied model of 2-D static electro-magnetic field and calculates the braking forces by means of finite element analysis software,and also analyzes effects on braking characteristics produced by current, air gap and speed. It could provide some references for design of eddy current brake magnet.

eddy current brake; braking force; finite element simulation; high speed train

1008-7842 (2015) 06-0025-03

*铁道科学技术研究发展中心科研项目(J2013J008)

男，工程师(

2015-06-20)

U260.35+7

A

10.3969/j.issn.1008-7842.2015.06.06