蒸汽发生器非线性支承系统的抗震能力分析

蔡逢春，梁艳仙，叶献辉

(1.中国核动力研究设计院 核反应堆系统设计技术重点实验室，四川 成都 610041；2.成都航空职业技术学院，四川 成都 610021)



蒸汽发生器非线性支承系统的抗震能力分析

蔡逢春1，梁艳仙2，叶献辉1

(1.中国核动力研究设计院 核反应堆系统设计技术重点实验室，四川 成都 610041；2.成都航空职业技术学院，四川 成都 610021)

计算核电厂设备的高置信度低失效概率(HCLPF)抗震能力是地震概率安全评价、地震裕度评价的一个重要步骤。以蒸汽发生器支承为研究对象，建立其详细的非线性有限单元模型，通过逐步增大地面运动水平，反复计算系统的响应，最后得到蒸汽发生器支承的抗震能力，并与通过确定性失效裕度法得到的HCLPF进行比较。结果表明，两者的计算结果差别较大。本文建议对于非线性较强的设备需采用非线性时程分析方法计算设备的HCLPF。

抗震能力；易损性；高置信度低失效概率；地震裕度评价

由于地震的发生有很大的随机不确定性，加上目前人类认知水平有限，使得在核电厂附近有可能发生超设计基准的地震，最近几年就发生了两起，一个是福岛的“3·11”事故，另一个是发生在美国北安娜核电厂附近的5.8级地震。

对于核电厂超设计基准的地震事故，通常采用地震概率安全评估(SPSA)或地震裕度评估(SMA)的方法进行核电厂的地震安全评价，这两种方法已被广泛应用于核电厂的地震安全评估[1-3]。通过SPSA分析可得到核电厂系统、部件和构筑物的抗震能力，还可得到电厂堆芯损伤风险和对公众产生不利影响的风险，必须采用概率易损性的方法来计算结构和设备的易损性曲线和高置信度低失效概率(HCLPF)抗震能力。SMA方法只关注设备、部件和电厂的抗震能力，该方法可使用概率易损性方法或保守的确定性失效裕度(CDFM)方法来计算设备的HCLPF，这使得地震裕度评估方法简单易懂，易于交流。

但对于非线性较强的系统，这些方法并不太适用。Watanabe等[4]研究带有支承环的竖向U型管热交换器概率易损性参数，采用非线性时程分析方法确定了热交换器的抗震能力。Nakamura等[5]采用非线性三维模型研究了反应堆厂房的易损性，并将非线性三维计算结果与集中质量的简化模型的计算结果进行了比较，结果表明简化模型的计算结果偏大。Kim等[6]采用数值模拟方法研究了核电厂系统易损性的不确定性，并采用系统HCLPF来检验不确定性分析的收敛性。Huang等[7]发展了一种地震风险评价的新方法，该方法采用基于响应的易损性曲线来描述核电厂结构和非结构部件的抗震能力，部件响应采用非线性时程分析方法计算得到，并采用Monte Carlo法确定部件的损伤状态，可以考虑部件之间的相关性。

通过上述研究可看出，一些研究者开始使用更加准确的非线性三维模型分析构筑物、设备和部件的抗震能力。综合考虑材料、间隙等非线性因素，并采用非线性时程分析方法，通过逐步增大地面运动水平找到构筑物、设备和部件的抗震能力，这种方法得到的HCLPF更加准确。

本文以蒸汽发生器支承为对象，采用非线性时程分析方法计算其HCLPF，并与CDFM方法结果进行对比。

1 设备HCLPF的计算方法

1.1 概率易损性方法

易损性评价的目的是根据地面运动参数，如峰值地面运动加速度或谱加速度，评价给定部件的抗震能力。通常，电厂场地的地震危害性通过峰值地面加速度或在不同结构频率处的谱加速度来定义。因此所有的易损性评价是以地面加速度(峰值地面加速度或谱加速度)为参考的。

通常认为构筑物、设备的抗震能力服从对数正态分布。“S”形的对数正态分布很好地模拟了系统、结构和部件的真实易损性分布，且在数学上能较为方便地分析概率分布，可通过两个参数进行描述：中值抗震能力Am和对数标准差βR。一旦确定了Am和βR，就可计算在不同地面运动水平条件下的失效条件概率。

给定一特定的失效模式，构件的易损性曲线可通过地面加速度抵抗能力中值和两个随机变量表示[8-10]：

A=AmeReU

(1)

式中：A为构件的抗震能力，m/s2；eR和eU为中值为1的随机变量，分别表示中值的内在随机性(偶然不确定性)和知识不确定性(认知不确定性)。在该模型中，假设eR和eU服从对数正态分布，其对数标准差分别为βR和βU。

如果只考虑随机变量βR，在给定峰值地面加速度水平a的条件下，设备失效条件概率f0为：

(2)

式中，Φ( )为标准正态分布概率累积分布函数。

当考虑不确定性参数eU时，易损性f就成了随机变量。在每个加速度处，f将被表示成一主观概率密度的函数。在给定a条件下，构件的f0为：

(3)

式中：Q为主观概率(置信度)，通过该值可得到1组易损性曲线；Φ-1( )为标准正态分布概率累积分布函数的反函数。

易损性曲线还可通过组合变量标准差βc来描述：

(4)

将βc代入式(2)可得易损性曲线，该曲线也叫均值易损性曲线。

核电厂的构筑物、设备和部件的抗震能力通常用HCLPF来表示。HCLPF是指在具有95%置信度的易损性曲线上，对应具有5%失效概率的地面运动水平，因此将f0=0.05、Q=0.95或f0=0.01、Q=0.95代入式(3)，可得到设备的HCLPF：

(5)

(6)

确定构筑物系统和部件(SSC)的HCLPF，关键是要确定Am、βR、βU和βc。在计算易损性参数时，基于中间变量(安全比例因子)开展计算，SSC的抗震能力可定义为：

(7)

式中：F为安全比例因子，为构件的真实抗震能力与安全停堆地震(SSE)引起的响应的比值；ASSE为SSE地面峰值加速度，m/s2。F可进一步分解为与材料强度、材料延性以及构筑物和设备分析模型相关的因子进行计算。

1.2 CDFM方法

CDFM方法是从概率易损性方法简化而来，该方法不需要计算概率易损性参数，而是确定适当的输入参数，然后通过确定性计算方法得到设备的HCLPF。根据文献[11]，采用CDFM方法需要的计算输入包括以下内容。

1) 载荷组合：取正常运行载荷与审查级地震(RLE)载荷(或SSE载荷)。

2) 地面响应谱：取具有非超越概率为84%的谱形。

3) 阻尼：取保守的中值阻尼。

4) 结构模型：最佳估算的中值模型并考虑在频率上的不确定变化。

5) 土-结构耦合：最佳估算的中值模型并考虑参数的变化。

6) 材料强度：规范指定的最小强度，或是如果试验数据可得到，取具有95%超越概率的真实强度。

7) 评定方程：一般使用现行的规范、标准，如RCCM的D级准则。

8) 非弹性能量吸收：对于非脆性失效模式，且是线弹性的分析，那么在抗震能力分析中，需要将计算地震应力折减20%，以考虑材料延性的影响；或是进行非线性分析，使得材料达到超过95%的延性水平。

9) 楼板响应谱的生成：使用频率平移而不是峰值拓宽，以考虑不确定性，使用中值阻尼。

确定了以上的计算输入，采用CDFM法计算设备的HCLPF时，通常以RLE为参考，确定弹性比例因子FSE、Fμ，即可得HCLPF。

(8)

式中：C为部件的强度(也可以是载荷、位移等)，Pa；DNS为非地震载荷产生的应力，Pa；DS为RLE载荷产生的应力，Pa；ΔCS为RLE导致抗震能力的减少值，Pa。

采用CDFM法，HCLPF的计算表达式为：

(9)

式中：如果是延性失效，Fμ通常保守地取1.25，如果是脆性失效，Fμ取1；ARLE为RLE地震的峰值地面加速度，m/s2。

2 蒸汽发生器支承的HCLPF

上述几种计算设备HCLPF的方法是在实际工程上常用的方法，这些方法是以已有的地震分析(试验)结果(SSE或是RLE)为参考，通过线性比例放大方法计算设备的HCLPF，但对于非线性较强的系统这些方法并不太适用。

本文分别采用非线性时程分析方法和CDFM方法计算蒸汽发生器支承的HCLPF。蒸汽发生器支承示意图如图1所示，主要由3个部分组成：4个下部支承腿，下部横向支承由6个止挡块组成(编号分别为B1、B2、B3、B4、B5、B6)，上部横向支承由抱环和2个阻尼器组成。

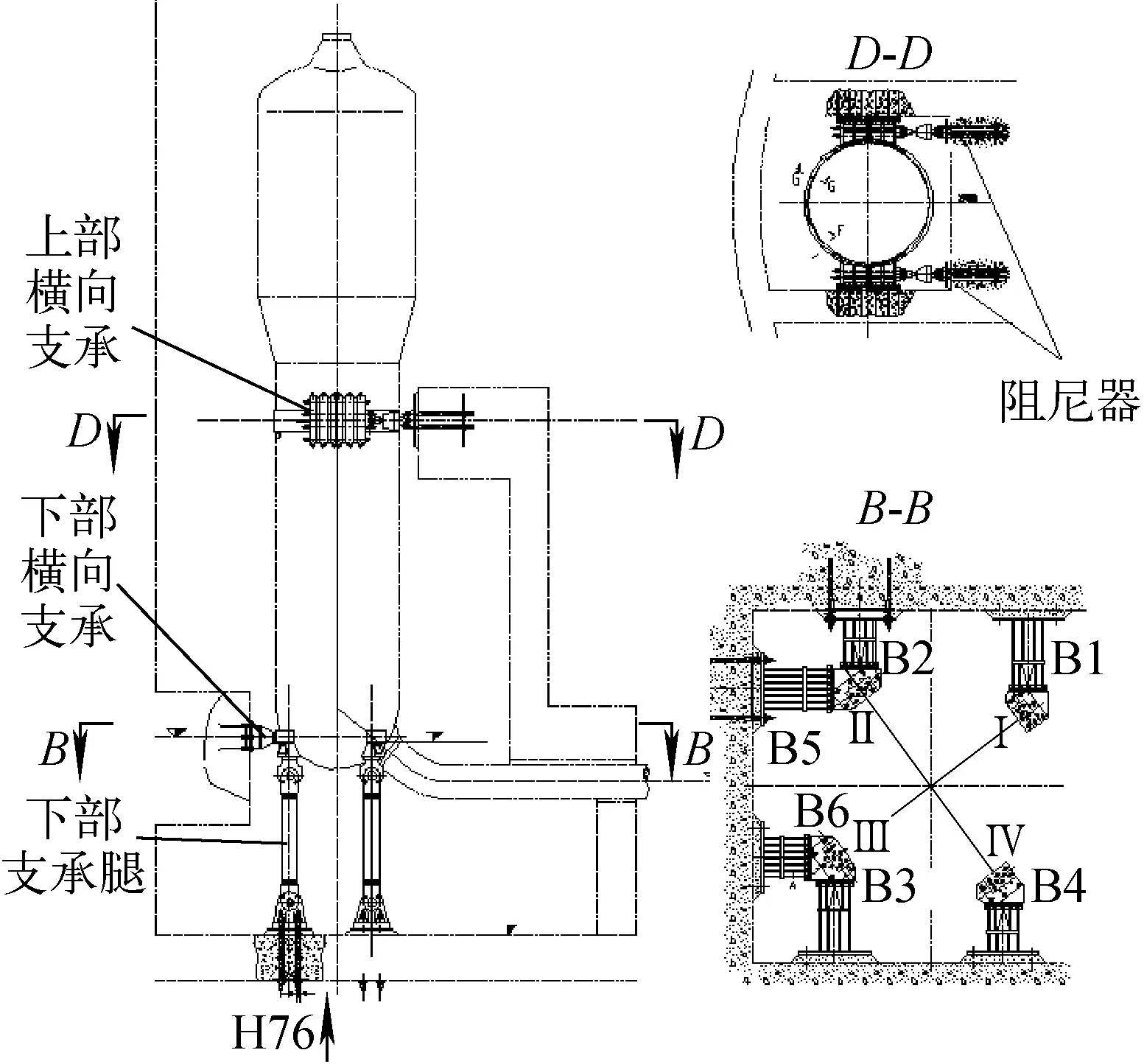
图1 蒸汽发生器支承示意图Fig.1 Scheme of support for steam generator

2.1 非线性时程分析方法

通常，蒸汽发生器的支承结构是典型的非线性系统，其非线性因素主要表现如下：支承腿的拉伸和压缩刚度不同，下部横向支承及上部横向支承是存在间隙的，且当地震载荷较大时，主管道材料会进入弹塑性，也会影响蒸汽发生器支承所受到的载荷。本文在计算蒸汽发生器支撑的抗震能力时，主要考虑支承腿拉压刚度双线性，上、下部横向支承的间隙非线性。对于主管道材料的非线性，材料本构关系采用各向同性硬化塑性的本构模型。

本文选取反应堆冷却剂主系统的一个环路作为分析对象(包括反应堆压力容器、主泵和主管道)来研究蒸汽发生器支承的抗震能力，有限元模型如图2所示，主要采用质量单元、管道单元、弯头单元、梁单元以及非线性弹簧单元模拟，模型参数取某一参考电厂[12]。环路模型在主设备的支承处耦连到反应堆厂房上，反应堆厂房结构采用梁单元模拟。

考虑地面运动水平较大，厂房结构会进入塑性，根据文献[7]，厂房结构阻尼比可取10%，设备的阻尼比可取5%。

为了寻找蒸汽发生器支承抵抗地震运动的能力，在厂房筏基位置施加地震加速度时程，采用非线性时程积分方法求解系统的响应，通过逐步线性放大筏基位置的加速度时程，反复计算系统的响应，直至蒸汽发生器支承受到的载荷超过其限值而失效，并记录蒸汽发生器在不同地面运动水平条件下所承受的载荷，如此反复计算，可以得到蒸汽发生器支承所承受的地震载荷随地面运动水平的变化曲线，最后通过支承的载荷限值确定其所能承受的地面运动水平。

图2 环路有限元模型Fig.2 Finite element model of loop

根据文献[13]可确定蒸汽发生器下部支承腿的载荷限值为883.6×104N，下部横向支承的载荷限值为940.7×104N，上部横向支承阻尼器载荷限值为18 000.0×104N，阻尼器方向的抱环载荷限值为1 226.1×104N。

图3为自由场峰值地面加速度(PGA)为0.1g条件下筏基位置3个方向的加速度时程。通过逐步线性比例放大该时程，反复计算系统响应，得到蒸汽发生器支承所承受的地震载荷随地面运动水平(PGA)的变化，如图4所示。

根据支承处的计算结果和限值可得到各支承部件的抗震能力，即HCLPF，下部支承腿为0.83g，下部横向支承大于1g，阻尼器为0.67g，上部支承抱环为0.46g。上述结果表明上部支撑的抱环最先失效。

2.2 采用CDFM方法计算支承的HCLPF

根据蒸汽发生器支承的应力分析报告[13]可得到支承在SSE载荷及自重载荷作用下的计算应力，以及相应的许用应力限值，基于CDFM方法，采用式(9)计算各支承部位的HCLPF，结果列于表1。

图4 下部支承腿(a)、下部横向支承(b)和上部横向支承(c)的载荷Fig.4 Load of lower support leg (a), lower lateral support (b) and upper lateral support (c)

表1 基于CDFM法得到的HCLPF
Table 1 HCLPF based on CDFM method

支承SSE响应/MPa自重响应/MPa许用限值/MPaFSEFμHCLPFHCLPFnon下部支承腿(上支承座)136.7175.46400.002.371.250.59g0.83g下部横向支承67.120.00225.003.351.250.84g>1g上部抱环73.350.00186.002.541.250.63g0.46g

注：HCLPFnon为非线性时程分析方法得到的HCLPF

2.3 分析与讨论

由表1可知，CDFM方法和非线性时程分析方法计算得到的HCLPF的差异较大，这主要是由系统中存在较强的非线性引起的。当外部地震载荷较大时，间隙关闭，蒸汽发生器与下部止挡块、上部抱环发生剧烈碰撞，载荷急剧增大。由于蒸汽发生器下部有主管道的约束，使得下部支承的载荷增长较慢，上部支承的载荷增长速度相对较快，故非线性时程分析方法计算得出上部抱环最先失效。而采用CDFM方法计算时，得到蒸汽发生器支承最先发生失效的是下部支承腿，这与实际不符，且计算值(0.59g)大于采用真实的非线性时程分析方法的计算值(0.46g)。因此对于非线性较强的设备，应采用非线性时程分析方法来计算HCLPF。

3 结论

概率易损性方法、CDFM方法是以已有的地震分析(试验)结果(SSE或RLE)为参考，通过安全比例因子，将参考地面运动水平放大到SSC的失效水平，从而确定SSC的HCLPF，参考地震的分析结果一般是基于线性方法得到的。而当地面运动水平很高时，材料可能进入塑性，结构还可能有间隙、几何非线性等因素，这些非线性因素会导致这些方法得到的结果不够准确，但这些方法相对较为简单，节省计算时间，容易在工程上应用。

本文采用非线性时程分析方法计算了蒸汽发生器支承的HCLPF，结果与CDFM方法的计算结果差异较大。因此对于非线性较强的设备，需建立分析对象的详细非线性模型，采用非线性时程分析方法逐步增大地面运动水平，寻找设备的抗震能力，从而确定设备的HCLPF。

[1] KENNEDY R P. Methodology for deriving seismic fragilities, TR-103959[R]. California: Electric Power Research Institute, 1994.

[2] KASSAWARA R. Seismic fragilitiy application guide, 1003121[R]. California: Electric Power Research Institute, 2002.

[3] KASSAWARA R. Seismic fragilitiy application guide update, 1019200[R]. California: Electric Power Research Institute, 2009.

[4] WATANABE Y, MURAMATSU K, OIKAWA T. Seismic capacity evaluation of a group of vertical U-tube heat exchanger with support frames for seismic PSA[J]. Nuclear Engineering and Design, 2005, 235(2): 2 495-2 512.

[5] NAKAMURA N, AKITA S, SUZUKI T, et al. Study of ultimate seismic response and fragility evaluation of nuclear power building using nonlinear three-dimensional finite element model[J]. Nuclear Engineering and Design, 2010, 240(3): 166-180.

[6] KIM J H, CHOI I K, PARK J H. Uncertainty analysis of system fragility for seismic safety evaluation of NPP[J]. Nuclear Engineering and Design, 2011, 241(1): 2 570-2 579.

[7] HUANG Yinnan, WHITTAKER A S, LUCO N. A probabilistic seismic risk assessment procedure for nuclear power plants, (Ⅰ) Methodology, (Ⅱ) Application[J]. Nuclear Engineering and Design, 2011, 241(5): 3 985-4 003.

[8] KENNEDY R P, RAVINDRA M K. Seismic fragilities for nuclear power plant risk studies[J]. Nuclear Engineering and Design, 1984, 79(3): 47-68.

[9] KENNEDY R P, CORNELL C A, CAMPBELL R D. Probabilistic seismic safety study of an existing nuclear power plant[J]. Nuclear Engineering and Design, 1980, 59(4): 315-338.

[10]PISHARADY A S, BASU P C. Methods to derive seismic fragility of NPP components: A summary[J]. Nuclear Engineering and Design, 2010, 240(6): 3 878-3 887.

[11]KENNEDY R P. A methodology for assessment of nuclear power plant seismic margin, NP-6041-SL[R]. California: Electric Power Research Institute, 1991.

[12]叶献辉. 反应堆冷却剂系统地震分析论证[R]. 成都：中国核动力研究设计院，2009.

[13]齐欢欢. 蒸汽发生器支承应力分析[R]. 成都：中国核动力研究设计院，2011.

Analysis on Seismic Capacity of Nonlinear Supports System of Steam Generator

CAI Feng-chun1, LIANG Yan-xian2, YE Xian-hui1

(1.ScienceandTechnologyonReactorSystemDesignTechnologyLaboratory,NuclearPowerInstituteofChina,Chengdu610041,China;2.ChengduAeronauticPolytechnic,Chengdu610021,China)

The calculation of the high confidence of low probability of failure (HCLPF) seismic capacity of equipments in nuclear power plants is an important process for seismic probability safety assessment and seismic margin assessment. In this paper, the seismic capacity of the supports of the steam generator was studied. A nonlinear model of the steam generator was built, and the seismic response of the system was calculated iteratively by scaling the ground motion level step by step. The seismic capacity of the supports of steam generator was obtained by this nonlinear time history analysis and was compared with the HCLPE based on the conservative deterministic failure margin method. The results show that the calculating values of two methods are different. The seismic capacity of equipments with nonlinearity should be calculated by nonlinear time history method.

seismic capacity; fragility; high confidence of low probability of failure; seismic margin assessment

2014-03-15;

2014-10-22

蔡逢春(1979—)，男，湖北咸宁人，高级工程师，博士，核能科学与工程专业

P315

A

1000-6931(2015)07-1260-06

10.7538/yzk.2015.49.07.1260