基于经典微扰理论的特征值灵敏度和不确定度分析

刘 勇，曹良志，吴宏春，祖铁军

(西安交通大学 核科学与技术学院，陕西 西安 710049)



基于经典微扰理论的特征值灵敏度和不确定度分析

刘 勇，曹良志，吴宏春，祖铁军*

(西安交通大学 核科学与技术学院，陕西 西安 710049)

核数据不确定度作为组件/栅元计算不确定度的重要来源，备受重视和研究。本文采用经典微扰理论，推导输运计算中keff对于核数据的灵敏度系数和不确定度的计算方法。基于ENDF/B-Ⅶ.1制作多群协方差数据库，并根据所采用的组件输运求解程序的截面模型对分反应道协方差矩阵进行归并。开发灵敏度和不确定度分析程序COLEUS，对传统压水堆燃料栅元进行计算分析。数值结果表明，栅元计算的keff对235U每次裂变中子产额的扰动最为敏感，238U俘获截面对keff不确定度的贡献最大。目前的核数据的不确定度会给keff带来0.4%～0.5%的不确定度。

微扰理论；协方差；灵敏度；不确定度

在核反应堆计算中，由于在计算模型、输入参数和经验修正等方面的不足，使得计算结果存在一定的不确定度。对重要参数灵敏度和不确定度的量化，不仅有利于确定合理的设计裕量，提高核反应堆设计的经济性，还可指导核数据评价的优化方向。

核反应堆的计算从最初的栅元(组件)计算到堆芯计算，再到最终的核反应堆系统计算的各个阶段，都存在不确定度的引入和传递[1]。作为核反应堆计算的基础，栅元(组件)计算的不确定度来源有如下3方面[2]：1) 模型、计算方法和近似引入的偏差；2) 反应堆系统的物理参数测量偏差，如密度、尺寸等；3) 基本物理参数的偏差，如截面数据等。而第3个方面中的中子反应截面被认为是该计算过程最重要的不确定度来源之一[3]。

目前国际上以UAM(uncertainty analysis in modelling)[1]等为代表的合作项目，正在广泛地开展针对反应堆计算敏感性和不确定性的分析。核数据的分析作为敏感性和不确定性分析中重要的一个环节，备受重视，其中的代表程序有TSUNAMI[4]、ERANOS[5]、SUSD3D[6]等。这些程序主要关注核数据的扰动和其测量不确定度导致的积分参数(keff、反应率、冷却剂空泡反应性系数等)的扰动和不确定度。近年来国内也在这方面展开研究工作，具有代表性的程序有SUCA1D[7]、SURE[8]等，但这些程序均限于一维计算，研究的积分参数类型也较为局限。因此，本文关注核数据对计算结果的影响，包括keff对核数据扰动的灵敏度以及在当前核数据的测量精度下keff的不确定度。基于经典微扰理论，采用子群共振方法程序SUGAR[9]和二维任意几何特征线输运程序AutoMOC[10]，开发灵敏度和不确定度分析程序COLEUS，并对栅元计算中keff对中子反应截面的灵敏度和中子反应截面的不确定度对keff造成的不确定度进行计算和分析。

1 理论方法

1.1 灵敏度系数计算方法

在反应堆物理栅元计算中，典型过程包括共振计算和输运计算。如果只考虑参数α的扰动在输运方程中的作用，这种直接影响称为显式敏感性；如果考虑参数α在共振计算过程中对共振截面的作用，继而间接影响到输运方程的求解，这种间接影响称为隐式敏感性[11]。本文主要关注显式灵敏度系数及其不确定度的计算，在确定论方法中，显式灵敏度系数的计算常采用微扰理论[12]。

中子输运方程的算子形式为：

(1)

其中：φ=φ(r，Ω，E)为中子角通量密度；λ为方程的特征值，λ=1/keff；M为输运算子；F为裂变源项算子；L为输运算子中除裂变源项算子以外的其他算子。

中子输运方程的共轭方程为：

(2)

其中：φ*=φ*(r，Ω，E)为共轭中子角通量密度；M*为输运算子的共轭算子；F*为裂变源项算子的共轭算子；L*为输运算子中除裂变源项算子以外的其他算子的共轭算子。

给系统一个微小的扰动后，算子M变成M′=M+δM，或记作：

(3)

P=δM称为扰动算子。设扰动后的中子通量密度φ′满足：

(4)

或

(5)

将扰动前的中子共轭通量密度φ*同式(5)两端作内积，得到：

(6)

其中，〈·，·〉表示在相空间作内积。由于M*和M共轭，并假定边界条件未受到扰动，则有：

(7)

而M*φ*=0，于是得到：

(8)

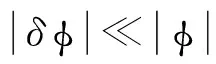
(9)

式(9)称为扰动方程。

由于M=L-λF，则：

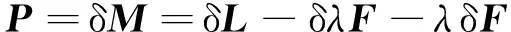
(10)

将式(10)代入式(9)，得：

(11)

从而有：

(12)

由于λ=1/keff，所以：

(13)

根据灵敏度系数的定义[1]，有：

(14)

从式(14)可看出，式中算符对核数据的偏导项容易求得，所以只需一次前向输运计算和一次共轭输运计算得到前向中子角通量密度和共轭中子角通量密度，就能得到keff对包含在输运算子中的所有参数的灵敏度系数。本文采用子群共振方法程序SUGAR进行共振计算，采用二维任意几何特征线输运程序AutoMOC进行前向输运计算，以获得中子角通量密度；并对该输运程序进行改进，获得中子共轭角通量密度，然后根据式(14)计算keff对核素各种截面的灵敏度系数。

1.2 不确定度计算方法

keff可认为是截面的函数，写成如下函数形式：

(15)

将keff在σi的期望值σi0处进行泰勒一阶展开：

(16)

设σi的方差为V(σi)，keff的方差为V(keff)，对式(16)等号两边取方差得到：

(17)

其中，cov(σi，σj)为σi和σj的协方差，用来衡量两个变量的总体误差。式(17)即为不确定度传播率，该式将截面数据的不确定度传递给keff。

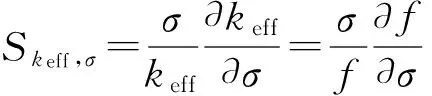
(18)

(19)

1.3 协方差数据

早期核数据的评价库往往只给出核数据的一阶矩，即期望值。从ENDF/B-Ⅳ开始，评价库中就包含了一些核素的核数据的概率分布的二阶矩，即协方差[14]，包括每次裂变的中子产额、共振参数、中子截面、次级粒子能量和角度分布、放射性核素产额等数据的协方差信息[1]。协方差数据文件提供了核数据的相关性和不确定度。从式(19)可看出，只要得到核数据的相对协方差信息，就能结合灵敏度系数，通过Sandwich Rule公式，计算积分参数(如keff)的不确定度。

NJOY制作的多群协方差数据是各种分反应道的协方差数据，而大多基于确定论的中子输运计算程序使用的截面模型是将各分反应道截面以求和形式给出的散射、俘获截面，因此需要散射、俘获截面的协方差，这样的协方差数据无法从NJOY直接得到。一般有3种方法处理这种问题[3]：1) 修改程序的截面模型；2) 使用同问题无关的截面数据来计算keff对各反应道截面的灵敏度系数；3) 制作与输运程序截面模型一致的协方差数据库。本文采用第3种方法，将制作的分反应道协方差信息转换成这种求和形式的截面的协方差信息。本文采用的截面模型中，俘获截面为：

(20)

其中，NG为能群总数。

由于俘获截面和散射截面同其分反应道截面是线性关系，所以由向量的协方差计算关系式可知：

(21)

其中：Kc为NG×8NG的系数矩阵；cov(σKc)为各反应道之间8NG×8NG的协方差矩阵。

本文采用的散射截面模型的形式为：

g=1，NG

(22)

同样可知：

(23)

其中：Ks为NG×4NG的系数矩阵；cov(σKs)为各反应道之间4NG×4NG的协方差矩阵。

基于ENDF/B-Ⅶ.1制作的172群协方差数据库中，俘获反应的分反应道中存在协方差数据的中子核反应包括(n，2n)、(n，3n)和(n，γ)反应。评价库中无其他分反应道协方差信息，假设为零。图1为基于ENDF/B-Ⅶ.1制作的238U的172群俘获反应各分反应道的相对协方差与归并得到的俘获截面的相对协方差矩阵。

由于(n，2n)和(n，3n)反应为阈能反应，所以图2只示出了前10能群的俘获截面及其分反应道截面随能群的变化曲线。

图1 238U俘获截面及其分反应道截面的相对协方差矩阵Fig.1 Relative covariance matrices corresponding to total capture cross section and individual capture cross section of 238U

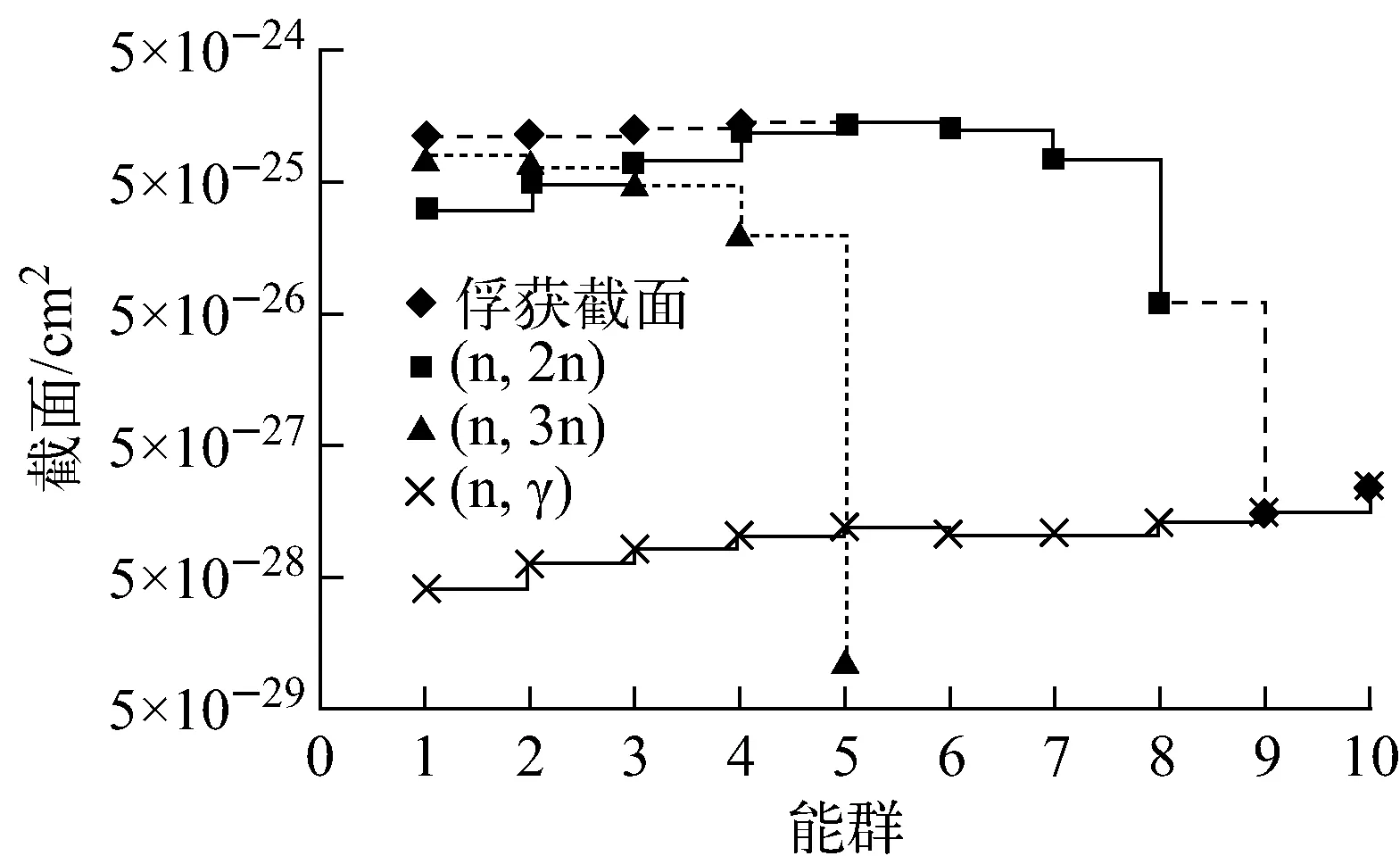
图2 238U前10能群俘获截面及其分反应道截面Fig.2 Total capture cross section and individual capture cross section of first ten energy groups of 238U

从图1、2可发现，虽然238U(n，γ)反应的相对协方差在高能群较大，但由于其截面值小，所以在归并成俘获截面相对协方差后，(n，γ)反应高能群相对协方差对俘获截面相对协方差的贡献并不大。俘获截面高能群的相对协方差主要来自(n，2n)和(n，3n)反应。值得注意的是，核数据的协方差大小并不能最终决定其对结果的不确定度贡献，这需要结合灵敏度进行计算。

基于上述理论分析，本文敏感性和不确定性分析的计算流程图如图3所示。

图3 敏感性和不确定性计算流程图Fig.3 Flow chart of sensitivity and uncertainty calculation

2 计算结果

利用本文开发的程序COLEUS，对典型轻水堆燃料栅元进行灵敏度和不确定度分析，该问题来自OECD UAM LWR基准题[1]：TMI-1压水堆燃料组件栅元。

表1列出了该问题前向和共轭keff的计算结果，以及截面数据导致的keff相对不确定度的计算结果，本文用Δkeff(标准偏差)表示keff的不确定度，Δkeff/keff表示keff的相对不确定度。其中TSUNAMI-1D和CASMO-4的结果均来自文献[3]，二者输运计算采用的截面数据库基于ENDF/B-Ⅵ，本文采用的数据库基于ENDF/B-Ⅶ.0制作。本文计算得到的keff的总不确定度为0.416 7%，较参考结果偏小。其原因是本文采用的核数据相对协方差与参考结果采用的相对协方差数据有部分不一致，此外能群结构对于灵敏度系数和协方差矩阵的制作也存在影响，同样会导致不确定度计算结果的差异。但可发现，当前核数据的精度在传统压水堆栅元计算中对keff造成的不确定度在0.5%左右。

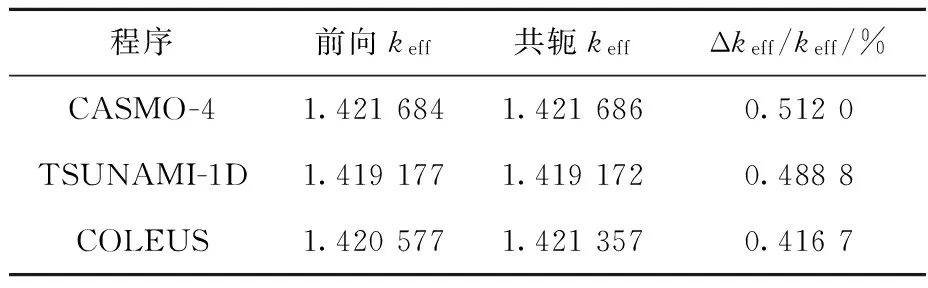
表1 keff及其不确定度计算结果Table 1 Calculation results of keff and its uncertainty

表2 PWR栅元中重要的不确定度来源及相对灵敏度系数Table 2 Most important sources of uncertainty in PWR pin-cell case and relative sensitivity coefficients

图4 重要反应的灵敏度系数Fig.4 Sensitivity coefficients of some important reactions

3 小结

微扰理论是计算微小扰动对响应影响的有效方法。基于经典微扰理论，开发了灵敏度和不确定度计算程序COLEUS，采用该程序分析了栅元计算中keff对各核素截面数据的灵敏度系数以及各核素截面对keff不确定度的贡献。

计算结果表明，截面不确定度对keff不确定度的贡献取决于灵敏度系数和协方差数据，keff对235U的每次裂变中子产额的扰动最为敏感，而238U俘获截面对keff的不确定度的贡献最大。目前核数据的测量精度会给传统压水堆UO2燃料栅元计算keff带来0.4%～0.5%的不确定度。

[1] IVANOV K, AVRAMOVA M, KAMEROW S, et al. Benchmarks for uncertainty analysis in modelling (UAM) for the design, operation and safety analysis of LWRs, Vol Ⅰ: Specification and support data for neutronics cases (Phase Ⅰ), Version 2.1 (final specifications)[R]. [S. l.]: OECD Nuclear Energy Agency, 2013.

[2] WEISBIN C R, MARABLE J H, LUCIUS J L, et al. Application of FORSS sensitivity and uncertainty methodology to fast reactor benchmark analysis[R]. Oak Ridge: Oak Ridge National Laboratory, 1976.

[3] PUSA M. Incorporating sensitivity and uncertainty analysis to a lattice physics code with application to CASMO-4[J]. Annals of Nuclear Energy, 2012, 40(1): 153-162.

[4] REARDEN B T, HOPPER C M, ELAM K R, et al. Applications of the TSUNAMI sensitivity and uncertainty analysis methodology[C]∥ICNC2003. Tokai, Ibaraki, Japan: Japan Atomic Energy Research Institute, 2003.

[5] TAMAGNO P, Van ROOIJEN W F G, TAKEDA T, et al. Sensitivity analysis of Monju using ERANOS with JENDL-4.0[C]∥PHYSOR 2012. Knoxville, Tennessee, USA: American Nuclear Society, 2012.

[6] KODELI I. Multidimensional deterministic nuclear data sensitivity and uncertainty code system: Method and application[J]. Nuclear Science and Engineering, 2001, 138(1): 45-66.

[7] 刚直，周培德. 由截面不确定度引起积分参数keff不确定度一维分析程序开发[C]∥第十二届反应堆数值计算与粒子输运学术会议. 合肥：中国核学会，2008.

[8] 胡泽华，王佳，孙伟力，等. 基准模型keff对核数据的灵敏度分析及不确定度量化[J]. 原子能科学技术，2013，47(增刊)：312-317.

HU Zehua, WANG Jia, SUN Weili, et al. Sensitivity and uncertainty analysis of calculatedkeffon benchmark models due to uncertainties of nuclear data[J]. Atomic Energy Science and Technology, 2013, 47(Suppl.): 312-317(in Chinese).

[9] 刘庆杰. 二维任意几何子群共振计算方法研究及其应用分析[D]. 西安：西安交通大学，2010.

[10]陈其昌. 任意几何特征线方法及其在直接循环堆组件计算中的应用研究[D]. 西安：西安交通大学，2010.

[11]WILLIAMS M L, BROADHEAD B L, PARKS C V. Eigenvalue sensitivity theory for resonance-shielded cross sections[J]. Nuclear Science and Engineering, 2001, 138(2): 177-191.

[12]谢仲生，邓力. 中子输运理论数值计算方法[M]. 西安：西北工业大学出版社，2005.

[13]BALL M R. Uncertainty analysis in lattice reactor physics calculations[D]. McMaster: McMaster University, 2012.

[14]MacFARLANE R E, MUIR D W, BOICOURT R M, et al. The NJOY nuclear data processing system, Version 2012[R]. USA: Los Alamos National Laboratory, 2012.

[15]WILLIAMS M L, WIARDA D, ARBANAS D, et al. SCALE nuclear data covariance library[R]. Oak Ridge: Oak Ridge National Laboratory, 2009.

[16]MERCATALI L, IVANOV K, SANCHEZ V H. SCALE modeling of selected neutronics test problems within the OECD UAM LWR’s benchmark[J]. Science and Technology of Nuclear Installations, 2013, 2013: 1-11.

[17]KAMEROW S, IVANOV K, MORENO C A. Uncertainty analysis of light water reactor unit fuel pin cells[C]∥2011 International Conference on Mathematics and Computational Methods Applied to Nuclear Science and Engineering. Rio de Janeiro, RJ, Brazil: American Nuclear Society, 2011.

Eigenvalue Sensitivity and Uncertainty Analysis Based on Classical Perturbation Theory

LIU Yong, CAO Liang-zhi, WU Hong-chun, ZU Tie-jun*

(SchoolofNuclearScienceandTechnology,Xi’anJiaotongUniversity,Xi’an710049,China)

The uncertainty of nuclear data is being paid to more and more attention because it is one of the most important uncertainty sources in lattice calculation. The expressions of sensitivity and uncertainty ofkeffwith respect to the cross sections were deduced based on the classical perturbation theory. A covariance library was made based on ENDF/B-Ⅶ.1, and the individual covariance matrices of cross section were combined according to the cross section model for lattice calculation in this work. A code COLEUS (calculation tool for evaluating uncertainty and sensitivity) was developed for the sensitivity and uncertainty analysis, and a traditional PWR fuel pin cell problem was calculated and analyzed. Numerical results indicate thatkeffof lattice calculation is the most sensitive to the perturbation of the average number of neutrons released per fission of235U, while the capture cross section of238U has the biggest contribution to the final uncertainty. The measuring accuracy of present nuclear data will bring an uncertainty about 0.4%-0.5% forkeff.

perturbation theory; covariance; sensitivity; uncertainty

2014-03-25;

2014-07-15

国家自然科学基金资助项目(91226106)

刘 勇(1988—)，男，四川成都人，博士研究生，核能科学与工程专业

*通信作者：祖铁军，E-mail: tiejun@mail.xjtu.edu.cn

TL32

A

1000-6931(2015)07-1247-07

10.7538/yzk.2015.49.07.1247