几类具代数或指数衰减的层问题
杨雪洁, 周有顺
(安徽师范大学 数学计算机科学学院,安徽 芜湖 241003)
几类具代数或指数衰减的层问题
杨雪洁, 周有顺
(安徽师范大学 数学计算机科学学院,安徽 芜湖 241003)
主要研究了几类二阶非线性方程的奇摄动Dirichlet问题的边界层和角层现象.在适当的条件下,利用界定函数法和微分不等式理论证明了这几类问题呈边界层和角层性态的解的存在性,并给出了解的渐近估计.
奇摄动;边界层;角层;微分不等式理论
引 言
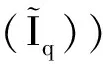
εy″=F(t,y,y′),
(1)
y(a,ε)=A,y(b,ε)=B
(2)
的解的边界层及内层现象,并给出该问题在不同条件下的解在边界层和内层处呈指数型衰减或呈代数型衰减的性态.假设:
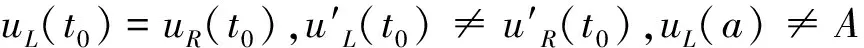
(3)
1 相关定义及引理
为了叙述方便,仿文献[8],对满足假设[H1]的上述退化轨道u=u(t),给出如下定义:

且在D0(u)中
其中正值连续函数d(t,δ1)满足
(4)
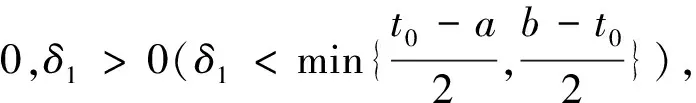
且在D1(u)中
其中d(t,δ1)与定义1中一致.
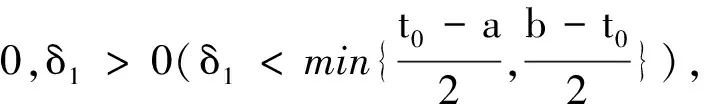
且在D2(u)中
其中d(t,δ1)与定义1中一致.

Fy′(t,y,y′)≥0.
Fy′(t,y,y′)≤0,
其中D(u):={(t,y,y′)|a≤t≤b,t≠t0,|y-u(t)|≤d(t,δ1),|y′|<+∞},d(t,δ1)与定义1中一致.
定义5[9]设α(t),β(t)∈C[a,b],在[a,b]上α(t)≤β(t),F(t,y,y′)∈C([a,b]×[α(t),β(t)]×R),称F(t,y,y′)在[a,b]上关于α(t)和β(t)满足Nagumo条件,如果存在[0,+∞)上的连续函数φ(s)>0,使得对于a≤t≤b,α(t)≤y≤β(t),|y′|<+∞,有
|f(t,y,y′)|≤φ(|y′|)
且
引理[10]如果存在连续函数α(t),β(t)满足
α(t)<β(t),t∈(a,b),
α(a)≤A≤β(a),
α(b)≤B≤β(b),
另外,存在[a,b]的某个分划:a=t0 α″(t)≥F(t,α(t),α′(t)), (5) β″(t)≤F(t,β(t),β′(t)), (6) 有解y=y(t)∈C2[a,b],使得在[a,b]上有α(t)≤y(t)≤β(t). 为了叙述方便,给出如下假设: [H2]F,Fy,Fy′∈C(D(u)),其中D(u)与定义4中一致,在[a,b]×R2的紧子集内,Fy′(t,y,y′)有界,且当(t,y)∈[a,b]×R的紧子集时,有F(t,y,y′)=O(y′2),(|y′|→+∞). 定理1 假设[H1]和[H2]成立,(3)式定义的退化轨道u=u(t)在[a,b]上是局部弱稳定且(Iq)稳定的,则存在ε0>0,使得当0<ε≤ε0时,问题(1)-(2)在[a,b]上存在解y=y(t,ε),满足 |y(t,ε)-u(t)|≤WL(t,ε)+VI(t,ε)+Γ(ε), 其中 证明 下文中的EST代表当ε→0+时的指数型小项. α(t,ε)=u(t)-WL(t,ε)-Γ(ε), β(t,ε)=u(t)+WL(t,ε)+VI(t,ε)+Γ(ε). 显然 令δ0=min{δ1,δ2},其中δ1,δ2分别由定义1和定义4给出.下证当t∈[a,t0)∪(t0,b]时,有 εβ″-F(t,β,β′)≤0 (12) 和 εα″-F(t,α,α′)≥0. (13) (14) (15) 其中ξ是介于u′与β′之间的任意一点,故取定 r=2C1+max{‖u″L‖,‖u″R‖} (16) 其中 另一方面,当t∈[a,b]时,对(16)取定的r>0,只要 就有 (17) 又由于 所以存在ε4>0,使得当t∈[a,b]且0<ε<ε4时,有 (18) (19) 故当0<ε≤min{ε2,ε3,ε4,ε5}且a≤t≤b时, WL+VI+Γ(ε) (20) 从而在[a,t0)∪(t0,b]上有 (21) Fy′(t,y,ξ)≥0, (22) Fy′(t,y,ξ)≤0, (23) 其中ξ2介于u′与β′之间,η2介于u和β之间,对(16)式给定的r>0,当0<ε≤ε0时,(14),(15)及(21)式成立,故 其中‖u″‖=max{‖u″L‖,‖u″R‖}. 综上所述,对(16)式给定的r>0,当0<ε≤ε0时,对一切t∈[a,t0)∪(t0,b],都有(12)式成立. 同理对(16)式给定的r>0,当0<ε≤ε0时,对一切t∈[a,t0)∪(t0,b],(13)式也成立.于是由[H2]根据引理知情形(i)得证. α(t,ε)=u(t)-WL(t,ε)-VI(t,ε)-Γ(ε), β(t,ε)=u(t)+WL(t,ε)+Γ(ε). 仿情形(i)即可得证. u(t)≤y(t,ε)≤u(t)+WL(t,ε)+VI(t,ε)+Γ(ε), 其中 证明 在[a,b]上定义 α(t,ε)=u(t), β(t,ε)=u(t)+WL(t,ε)+VI(t,ε)+Γ(ε). 显然(7)-(11)及(13)成立.下证(12)式. (24) (25) 其中ξ是介于u′与β′之间的任意一点.故取定 r=2C1+max{‖u″L‖,‖u″R‖} (26) 其中 其中ξ2介于u′与β′之间,η2介于u与β之间,对(26)式给定的r>0,当0<ε≤ε0时,(24),(25)及(21)式成立,所以 其中‖u″‖=max{‖u″L‖,‖u″R‖}. 综上所述对(26)式给定的r>0,当0<ε≤ε0时,对一切t∈[a,t0)∪(t0,b],都有(12)式成立.于是由[H2]根据引理知定理2得证. u(t)-WL(t,ε)-VI(t,ε)-Γ(ε)≤y(t,ε)≤u(t), 其中WL(t,ε),VI(t,ε),Γ(ε)与定理2中一致. 证明 在[a,b]上定义 α(t,ε)=u(t)-WL(t,ε)-VI(t,ε)-Γ(ε), β(t,ε)=u(t). 仿定理2即可得证. 例1 考虑边值问题 (27) y(-1,ε)=0,y(1,ε)=1. (28) |y(t,ε)-|t||≤WL(t,ε)+VI(t,ε)+Γ(ε), 其中 例2 考虑边值问题 (29) y(-1,ε)=1,y(1,ε)=1. (30) 经检验,本例满足定理2的所有条件,故问题(29)-(30)在[-1,1]上有解y=y(t,ε)满足 0≤y(t,ε)-|t|≤WL(t,ε)+VI(t,ε)+Γ(ε), 其中WL(t,ε),VI(t,ε),Γ(ε)与例1中一致. [1] 温朝晖,陈丽华,欧阳成,莫嘉琪.具有非线性边界条件的奇摄动微分系统边值问题[J].数学研究,2011,44(3):296-301. [2] YAO Jingsun, CHEN Lihua, WEN Zhaohui, MO Jiaqi. Solving method for the single-kink soliton solution to a disturbed coupled burgers system[J]. Chinese Physica Letters, 2011,28(8):1-4. [3] 刘树德,鲁世平,姚静荪,陈怀军.奇异摄动边界层和内层理论[M].北京:科学出版社,2012:51-57. [4] ZHOU Xianchun, YAO Jingsun, MO Jiaqi. Asymptotic solving method for sea-air coupled oscillator ENSO model[J]. Chin Phys B, 2012,21(3):5-9. [5] YAO Jingsun, LIN Wantao, DU Zengji, MO Jiaqi. Asymptotic solving method for period solution to a class of disturbed nonlinear evolution equation[J]. Chin Phys B, 2012,21(12). [6] 秦赵娜,姚静荪.具有局部弱稳定退化解二阶非线性方程的奇摄动问题[J]吉林大学学报:理学版,2013,51(5):819-825. [7] ZHOU Kehao, YAO Jingsun, QIN Zhaona. The angular layer phenomena for a class of singularly perturbed nonlinear boundary value problems[J]. Mathematica Applicata, 2013,26(4):881-887. [8] CHANG K W, HOWES F A. Nonlinear singular perturbation phenomena: theory and applications[M]. New York: Springer-verlag, 1974:26-71. [9] 倪明康,林武忠.边界层函数法在微分不等式中的应用[J].华东师范大学学报:自然科学版,2007,5(3):1-10. [10] 周明儒,杜增吉,王广瓦.奇摄动中的微分不等式理论[M].北京:科学出版社,2012:10-19. Several Classes of Problems with Algebraic or Exponential Decay Layers YANG Xue-jie, ZHOU You-shun (College of Mathematics and Computer Science, Anhui Normal University, Wuhu 241003, China) In this paper, we mainly study boundary layer and angular layer phenomenons for several classes of singulary perturbed Dirichlet problems of second-order nonlinear equations. Under certain conditions, the existence of the problems' solutions which exhibits boundary layer and angular layer behavior is proved and the asymptotic estimation of solutions is given by the method of bounding functions and the theory of differential inequalities. singular perturbation; boundary layer; angular layer; the theory of differential inequality 10.14182/J.cnki.1001-2443.2015.05.003 2015-01-10 国家自然科学基金(11271020). 杨雪洁(1989-),女,汉安徽阜阳人,硕士研究生,研究方向为奇异摄动理论及其应用. 杨雪洁,周有顺.几类具代数或指数衰减的层问题[J].安徽师范大学学报:自然科学版,2015,38(5):419-426. O175.14 A 1001-2443(2015)05-0419-08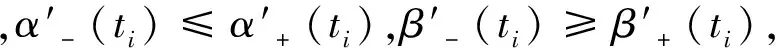
2 主要结果

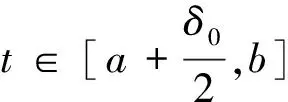






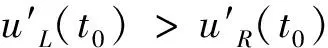

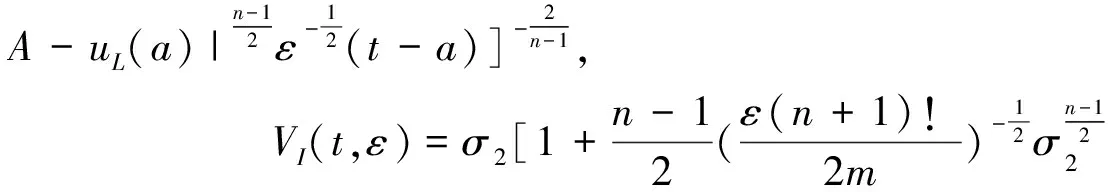
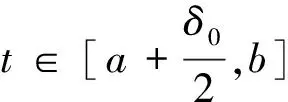
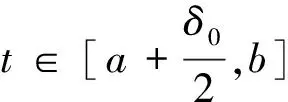
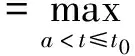

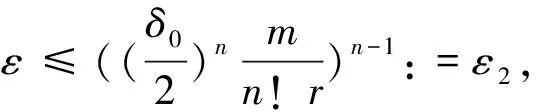


3 应用举例

——朱德军教授

