自立倒立摆系统的自摆起及稳定控制

刘继光，王丽军，袁 浩

（天津大学 电气与自动化工程学院，天津 300072）

倒立摆系统是自动控制领域的一个典型的控制对象，它的结构简单，成本较低，对象比较明确。倒立摆是非线性、强耦合多变量和自然不稳定的系统［1］，与其相似的旋转机架已在工程上广泛应用［2］，有着数种控制方案，如极点配置［3］、线性最优二次型［4］以及模糊控制［2］等。

近年来，对于倒立摆的控制研究也是控制领域的一大热点，其控制过程能有效地反映诸如可镇定性、鲁棒性、随动性以及跟踪等多种控制中的关键问题［5］。S.E.Oltean，等［6］利用当代的微处理器实现了基于模糊－比例微分的旋转倒立摆的自起摆控制；M.El－Bardini等［7］则提出了模糊－PID智能控制算法来对倒立摆系统进行控制；V.Kumar E等［8］对于倒立摆系统提出了鲁棒LQR控制方法；I.M.Arkhipova等［9］则是借助振动稳定性理论来对一个二级倒立摆系统进行平衡稳定控制。我国的李洪兴教授已经成功地实现了4级倒立摆控制的仿真实验及实物控制［10］，具有良好的稳定性和定位功能。这表明在倒立摆控制领域，我国在世界上已经达到了一定的技术水平。

本文通过对自立倒立摆的不同状态进行分析控制，应用开关控制器使得整个自立倒立摆系统能够从静止下垂的平衡位置起摆并稳定在不稳定的垂直倒立状态。

1 自立倒立摆系统

如图1所示，系统由SRV02－E伺服装置驱动。横臂的一端安装在伺服装置适当的齿轮轴上，用螺钉固定牢固。在横臂的另一端则安装了一根转轴，竖直的摆杆固定在这根转轴上，可以自由摆动。倒立摆摆杆的转角以及横臂的转角分别通过2个传感编码器测得。

本系统的控制目标是通过控制横臂摆动时摆杆平稳快速摆起，并最终将摆杆稳定在垂直倒立位置。

1.1 角度定义

图1 自立倒立摆系统物理模型

摆角的“full”角度αf的零位置对应初始时摆杆自然下垂状态，当摆逆时针旋转时αf增大，顺时针旋转时减小，其值可以超过360°，这一角度值可以从编码器得到。摆杆的“down”角度αd，它与αf相同定义，但要控制在±180°范围内。摆杆的“up”角度αu，其零角度对应于摆杆垂直倒立位置。当摆杆从垂直位置向左方向倾斜时，此角度对应为正值。

1.2 机理建模

对系统的2个自由度θ和α分别列写Lagrange方程。广义坐标为θ和α，广义力为转矩［11］。先对系统处于机架状态时建模得：

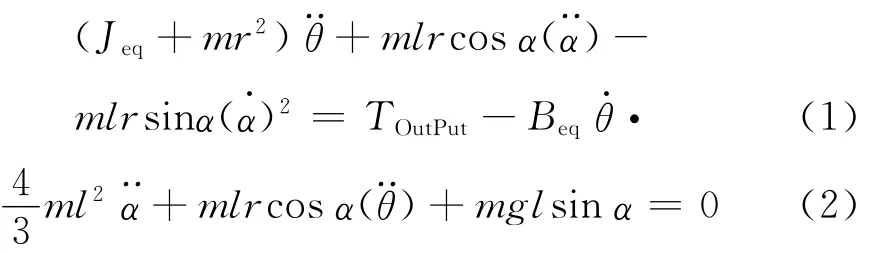
对（1），（2）进行线性化处理，因α很小，有cosα＝1，sinα≈α，得：

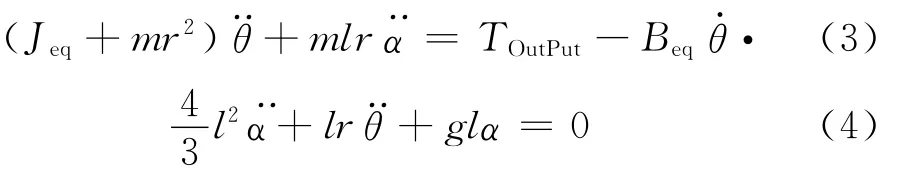
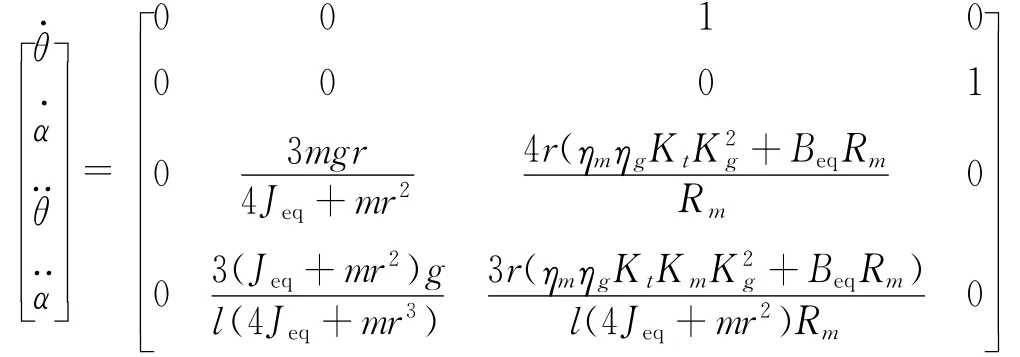
将系统的各参数值代入式（5）后得到

由于垂直倒立摆位置只是将摆杆反向倒立，故其方程与上式只是符号上的差别，垂直倒立位置的状态方程为

2 控制器设计

2.1 自摆起控制

倒立摆的自摆起控制实质上就是通过控制横臂的位置使倒立摆从下垂位置开始振荡。假设横臂偏离原来位置的角度为θ，摆杆偏离竖直状态的角度为θd，摆杆摆动的角速度为α·d，那么可以得到横臂与摆杆的关系为θ＝Pαd＋Dα·d。这样可以通过合适选择比例系数Kp和微分系数Kd的大小控制横臂摆动使倒立摆开始振荡，也就是说要基于摆杆的位置和速度来调整θ，最终通过横臂的左右摆动使摆杆完成自摆起。

为了将横臂固定在一定位置，需要设计一个PD控制器［12］：Vd＝Kp（θd－θ）＋Kdθ·，即设计一个闭环来控制电机的输出电压Vd，使θ最终达到θd。

通过多次实验得出，当 Kd＝0.55、Kp＝－0.01、P＝0.5、D＝0.001时，摆杆的摆起效果最好。自摆起控制器仿真结构图如图2所示。

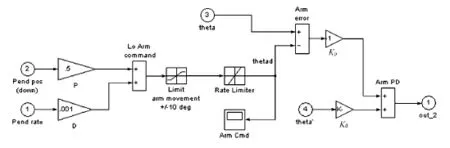
图2 自摆起控制器仿真结构图

要想让横杆快速摆起，最好的办法是给横臂加离散的力，即静止状态时给横臂力、当摆杆升到最高点时给横臂反方向力，这样效果最好。经过多次实验，得出控制激励仿真结构图如图3所示。

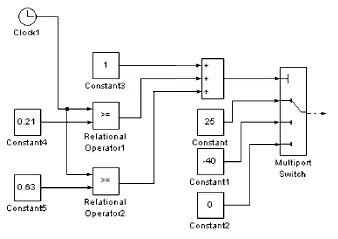
图3 自摆起控制激励仿真结构图

2.2 稳定控制器

本控制器采用LQR控制［13］。为了保证良好的控制效果，选择θ及其变化率θ·、α及其变化率α·这4个参数都进行控制。经过多次实验，选择Q＝diag［5 30 0 0］，R取1.5，在 Matlab里运行k＝lqr（A，B，Q，R）［14］，系统会自动计算出反馈矩阵K。

2.3 开关控制器

本文开关控制的目的在于判断是由自摆起控制器的输出反馈到电机还是由稳定控制器的输出反馈到电机。在初始状态时，应由自摆起控制器的输出反馈到电机，使摆杆起摆，当达到稳定控制器控制条件时，再由开关控制器决定把稳定控制器输出反馈到电机。

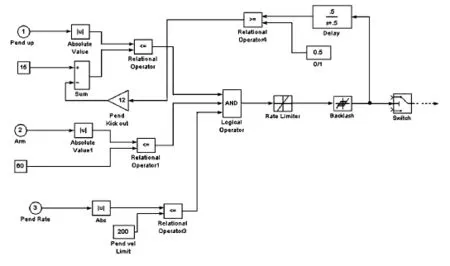
图4 开关控制仿真电路

2.4 仿真及实时控制

自立倒立摆系统的全部仿真电路如图5所示。仿真得到α及θ的波形分别见图6和图7。

在仿真的基础上，对自立倒立摆系统进行实时控制，首先通过由Quanser公司提供的嵌入到Matlab中的Wincon组件建立系统的实时控制模型，然后进行实时控制。运行仿真模型，发现摆杆并不能自摆到垂直倒立位置，这是因为模型的问题，导致激励给定的时间不准确，通过调整给定时间，并通过多次调试，得到实时控制的波形见图8和图9。

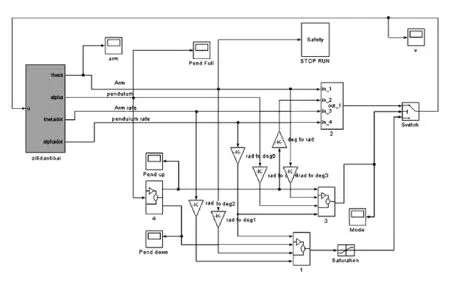
图5 系统完全仿真图

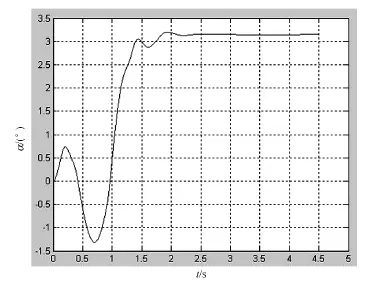
图6 α仿真图

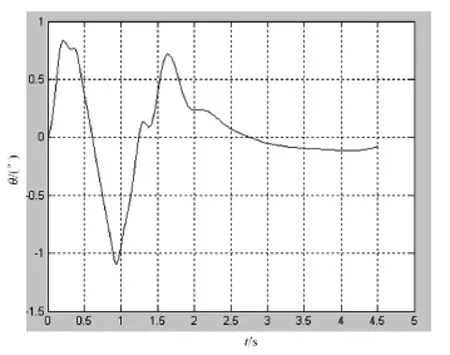
图7 θ仿真图

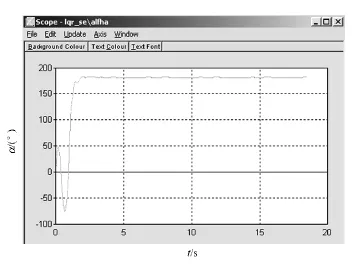
图8 α实际波形图

图9 θ实际波形图

由图8和图9可知，摆杆经过2次振动即可达到垂直倒立位置并稳定在该位置，并且具有一定的抗扰性，可见通过PD控制和LQR控制相结合的方法可以很好地控制自立倒立摆系统。

3 结束语

本文介绍了自立倒立摆的控制器的具体结合。该控制器共分为3个模块，分别是自摆起控制器、稳定控制器和变结构控制器。自摆起控制器主要为PID控制，使横杆能够平滑地摆起；变结构控制器为开关控制器，它将所有切换条件用一个与门连接，当所有条件都达到时会实现控制器的切换；稳定控制器为LQR控制器，将摆杆稳定在垂直倒立位置。本文成功实现了对一级旋转自立倒立摆的控制，具有良好的效果。

（

）

［1］王雪，柴毅，丁宝苍，等.自动控制原理开放性实验的开发［J］.实验室研究与探索，2011，30（7）：242－244.

［2］袁浩，陈晓倩，刘继光.二自由度旋转机架模糊控制策略探索［J］.实验技术与管理，2011，28（12）：32－35.

［3］袁浩，徐真真，王先来.极点配置方法在起重机机架模型中的应用［J］.实验室研究与探索，2006，25（12）：1492－1494.

［4］袁浩，乔宇亮，李保林，等.LQR控制策略在柔性关节系统中的实现［J］.实验技术与管理，2006，23（8）：33－35.

［5］黄苑虹.倒立摆系统的稳定性控制研究［D］.广州：广东工业大学，2002.

［6］Oltean S E，Duka A V.Balance control system using microcontrollers for rotational inverted pendulum［C］//The 7th International Conference Interdisciplinarity in Engineering.Procedia Technology，2014：11－19.

［7］El－Bardini M，El－Nagar A M.Interval type－2fuzzy PID controller for uncertain nonlinear inverted pendulum system［J］.ISA Tr asactions，2014（53）：732－743.

［8］V Kumar E，Jerome J.Robust LQR Controller Design for Stabilizing and Trajectory Tracking of Inverted Pendulum［J］.Procedia Engineering，2013（64）：169－178.

［9］Arkhipova I M，Luongo A，Seyranian A P.Vibrational stabilization of the upright statically unstable position of a double pendulum［J］.Journal of Sound and Vibration，2012，331（2）：457－469.

［10］李洪兴，苗志宏.四级倒立摆的变论域自适应模糊控制［J］.中国科学：E 辑，2002，32（1）：65－75.

［11］周衍柏.理论力学教程［M］.北京：高等教育出版社，1985：268－299.

［12］胡寿松.自动控制原理［M］.4版.北京：科学出版社，2001.

［13］刘豹.现代控制理论［M］.2版.北京：机械工业出版社，2000.272－282.

［14］黄忠霖.控制系统MATLAB计算及仿真［M］.北京：国防工业出版社，2000.