多塔高层建筑风荷载互扰效应研究*
涂佳黄, 梁经群, 黄 橙, 石晓东, 杨 雷, 王春磊, 张婷婷
(1. 湘潭大学 土木工程与力学学院, 湖南 湘潭 411105;2.湘潭大学 学生工作处, 湖南 湘潭 411105;3.北京市建筑设计研究院有限公司, 北京 100045;4. 北京国瑞兴业地产股份有限公司, 北京 100050)
多塔高层建筑风荷载互扰效应研究*
涂佳黄1*, 梁经群2, 黄 橙3, 石晓东1, 杨 雷4, 王春磊3, 张婷婷3
(1. 湘潭大学 土木工程与力学学院, 湖南 湘潭 411105;2.湘潭大学 学生工作处, 湖南 湘潭 411105;3.北京市建筑设计研究院有限公司, 北京 100045;4. 北京国瑞兴业地产股份有限公司, 北京 100050)
以鄂尔多斯国泰商务广场工程为背景,基于雷诺平均方法(RANS)和标准k-ε湍流模型,对多塔高层建筑周围的风场进行了数值模拟,得到不同风向角下建筑表面风载体型系数.然后,对串列与并列布置两种工况下的风场分布特性进行了分析,且阐明了塔楼之间风场的互扰机理.通过与风洞试验结果的对比表明数值模拟的结果能较准确地获取多塔高层建筑结构表面风压分布,为此类建筑结构的抗风设计提供一定依据.
多塔高层建筑;互扰效应;体型系数;风荷载
随着建筑高度和跨度的增加以及形状的复杂化,建筑物对风荷载的敏感度日益增大.但是,现行荷载规范中无法准确地提供相应设计参数的取值范围,如风载体型系数、结构表面的风压分布情况以及建筑群之间的互相影响系数等.近些年,这些问题引起了大批工程研究人员的极大兴趣,并取得了不少成果[1,2].
目前,学者们获取建筑物风荷载主要采用的方法是:现场实测、风洞试验和数值模拟.李秋胜等人[3]实测了台风“马莎”和“泰利”对台北101大楼的风致响应.雷静雅等人[4]采用风洞试验对超高层建筑的风荷载作用机理进行了系统的研究.冯永伟等人[5]采用风洞试验对双塔高层建筑之间的风荷载互扰效应进行了研究,发现了当双塔处于串列布置时,干扰效应影响十分明显.然而,上述两种方法费用高,难度大,周期长.随着计算机技术的发展和计算方法的进步,计算流体动力学数值风洞技术逐渐被工程技术人员所接受并运用于实际工程中[6~10].张敏等人[7]运用计算流体动力学方法对由四栋复杂形状高层建筑组成的建筑群进行了静力风荷载和风场的数值模拟计算,同时与风洞试验结果进行了对比,验证了数值方法的准确性.卢春玲等人[8]运用大涡模拟技术建立了深圳平安国际金融大厦的数值风洞全尺寸模型,并获取了三种不同风场条件下建筑表面平均/脉动风压以及风荷载时程数据.
本文基于Fluent软件平台,运用标准k-ε湍流模型对多塔高层建筑周围的风场进行了数值模拟,研究了串列与并列两种典型布置工况下,高层建筑风载体型系数的分布情况及其互扰效应,并与风洞试验结果进行了对比分析.
1 基本理论和参数选取
1.1 雷诺平均方程(RANS)
雷诺平均方法的主要思想为:将物理量分解成时均值和脉动值两个部分,然后将其带入Navier-Stokes(N-S)方程中,进行数学推导,得到N-S方程时均形式如下:
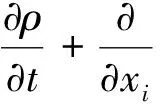
(1)
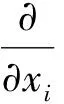
(2)

(3)
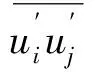
1.2 标准k-ε模型
大量研究表明,由于钝体绕流会产生分离、再附、冲撞、环绕、涡等一系列复杂的流动结构,湍流封闭模型是影响其数值模拟精度的关键因素之一.k-ε模型属于两方程模型范畴,通过引入湍动能k和耗散率ε对输运方程进行简化处理.首先,建立湍动粘度μt、湍动能k与耗散率ε三者的数学关系:

(4)
对于不可压缩流体的定常问题,将输运方程简化为:
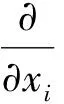
(5)
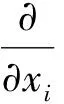
(6)
其中Pk是由平均速度梯度引起的湍动能,其表达式为:
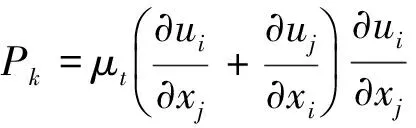
(7)
经研究发现,k-ε模型常数的合理取值分别为[11]:C1ε=1.44,C2ε=1.92,Cμ=0.09,σk=1.0,σε=1.3.
1.3 参数选取
本文风场边界条件分别选用:速度入口条件;完全发展出口条件;风场侧面和顶端为对称条件,即自由滑移壁面;结构表面和地面为无滑移壁面条件.数值计算中入口边界条件的速度剖面应尽可能与风洞试验一致,以便于进行计算结果的对比分析,验证本文风场参数的选取.
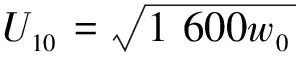
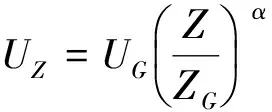
(8)
k=1.5(UZ×I)2,
(9)
ε=0.090.75k1.5/L,
(10)
式中,I和L分别为湍流强度与湍流积分尺度,现阶段,这两个参数在我国规范中没有给出明确的计算公式,本文借鉴了日本规范中记载的计算公式[12].本文采用的求解方法为SIMPLE算法,采用二阶迎风格式对动量方程与湍动能及湍动能耗散方程进行离散.计算过程中的收敛准则设定为10-4,且当各表面风压系数基本恒定时,才认为其风场达到了稳定状态.
2 多塔高层建筑风压分布
2.1 工程概述
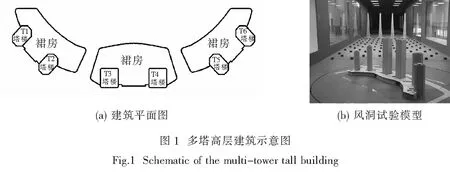
鄂尔多斯国泰商务广场项目位于康巴什新区人工湖南岸D区,总占地面积为270亩,总投资30亿元,总建筑面积近70万平方米,由6座商务大厦和大面积裙房组成,详见图1(a).塔楼的高度变化是从中间向两边逐渐降低:中间T3与T4两座塔楼最高达到240 m,其次是T2与T5两座塔楼180 m,最矮的塔楼T1与T6为140 m,裙房高度为23 m.风洞试验缩尺模型如图1(b)所示.
2.2 计算模型
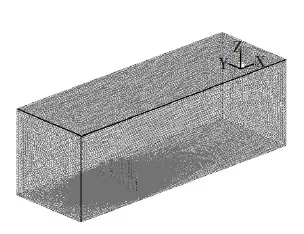
图2 计算域与网格划分
Fig.2 Computational domain and mesh division
计算风场区域的范围为3 000 m×1 500 m×1 000 m.为了消除风场边界对建筑物附近风场流动的影响,建筑物位于距风场入口内侧1/3处,同时风场大小设置满足阻塞率β<3%的要求.整个风场均采用四面体单元网格进行划分,且对建筑物周围风场网格进行了加密处理,如图2所示,计算网格总数约为1 500万,网格最小尺寸为0.5 m.
2.3 数值模拟结果
本文中主要给出60°和330°两个风向角的风洞试验结果与数值风洞结果的对比情况,风向角与建筑物的相关关系详见图3.两个风向角选取的原因是:60°风向角工况,即各塔楼大致为串列布置;330°风向角工况,即各塔楼为并列布置且上游区域无干扰建筑.通过建筑物表面风压变化以及风场分布特性,分析串列与并列布置两种工况下多塔建筑物风荷载互扰效应.

图4分别为240 m塔楼在60°风向角工况下(即此塔楼为迎风楼)数值风洞与风洞试验所得体型系数的对比情况.G面、I面和J面分别为侧面和背面,由于气流的分离作用和回流作用均以负压为主,数值风洞和风洞试验所得结果是一致的;迎风面上数值风洞和风洞试验结果存在一定差异,由于来风方向存在140 m和180 m两幢建筑的遮挡作用,导致240 m高层迎风面的正压分布区域不完整,也就是说来风方向的140 m和180 m两幢建筑削弱了240 m高层迎风面的风压力,这点上数值风洞也同样得出了这个趋势,只是在互扰效应的大小上与风洞试验结果存在一些差异,其正压的最大值基本一致.

图4 60°风向角时(迎风楼)数值模拟和风洞试验的风载体型系数云图对比
Fig.4 Comparison of wind loading shape coefficient nephograms between numerical simulation and wind tunnel test under wind angle 60°
图5分别为240 m塔楼在240°风向角工况下(即此塔楼为背风楼),数值风洞与风洞试验所得体型系数的对比情况.G面、H面和J面分别为侧面和背面,同其他工况一样,这三个面均以负压为主,而且数值上也较为接近;迎风面由于来风方向存在相同高度、相同体型建筑的遮挡作用,导致迎风面的正压分布并不完整.由图可见,数值结果和试验结果所得正压分布趋势是一致的,可是风洞试验所得的互扰效应较弱,局部竖向分布的正压强度仍然很大,且高于数值风洞结果.
图6分别为100 m、160 m和210 m高度处,建筑周围的压力分布和风场流线分布情况,选择这3个高度的原因是:100 m高度处可分析6个塔楼的相互影响,160 m高度处可分析4个塔楼的相互影响,210 m高度处则分析最高两个塔楼的相互影响.
由图可见,所有建筑沿着风向都存在着互扰影响,对240 m高的两个塔楼而言,迎风楼由于主要受到前方180 m高层的遮挡,迎风面的正压分布受到影响;240 m背风楼由于主要受到前方同高度建筑遮挡,可见背风楼的迎风面基本处于迎风楼尾部的回流区中,来流的撞击作用减弱,正压也会变弱,而且由于背风楼的迎风区域主要在回流区中,风速较低,导致背风楼侧面的分离作用也会减弱.

图5 240°风向角时(背风楼)数值模拟和风洞试验的风载体型系数云图对比
Fig.5 Comparison of wind loading shape coefficient nephograms between numerical simulation and wind tunnel test under wind angle 240°
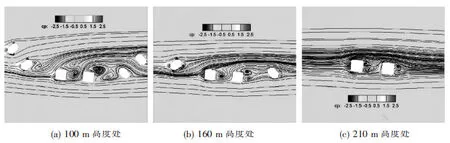
图6 60°风向角时不同高度处风压分布和流线分布
Fig.6 Distribution of wind pressure and streamline at different heights when wind angle 60°

图7 330°风向角时数值模拟和风洞试验的风载体型系数云图对比
Fig.7 Comparison of wind loading shape coefficient nephograms between numerical simulation and wind tunnel test under wind angle 330°
图7分别为240 m塔楼在330°风向角工况下,数值风洞与风洞试验所得体形系数的对比情况.由图可见:风洞试验和数值风洞的计算结果在数值大小与变化趋势方面都非常接近;H面为迎风面,因此以正压为主,数值上也非常相近;G和I面为侧面,由于气流的分离作用,该面以负压为主.图中可见大部分面积上负压的数值与风洞试验接近,只是迎风面边缘处的数值比较高,原因是数值模拟的计算点的尺度要比风洞试验测点的尺度精细得多,因此风洞试验无法详细监控局部很强分离作用产生的负压,此处虽不会影响整幢楼的整体受力,但是局部的维护结构设计时值得注意.如图8所示,由于所有建筑物基本都是沿着来风的垂直面水平展开的,并没有形成相互遮挡的效应,因此240 m高度的建筑基本为独立的迎风表现,即迎风面出现正压,流线撞击迎风面后向两侧绕流,并从迎风角部分离,产生较强负压,最终在建筑物尾部形成回流,致使尾部背风面产生负压.

图8 330°风向角时不同高度处风压分布和流线分布
Fig.8 Distribution of wind pressure and streamline at different heights when wind angle 330°
3 结 论
本文基于Fluent 软件平台,运用标准k-ε湍流模型对多塔高层建筑周围的风场进行了数值模拟,得到不同风向角下结构表面风载体型系数的分布情况,同时与风洞试验结果进行对比,验证了本文的数值模拟方法能较准确地反映出结构表面风压分布的变化趋势,可以为结构抗风设计提供一定的参考.
数值风洞模拟重点研究了240 m高的两个塔楼在并列和串列两种典型布置工况下,数值模拟结果和风洞试验结果的对比情况.研究发现,数值模拟结果与风洞试验结果在趋势上大体一致,且数值上也较为接近;并列布置时,迎风面以正压为主,侧面和背风面以负压为主,其中侧面角部强烈的分离作用造成强烈的负压区,局部的维护结构设计时应该注意;串列布置时,迎风楼的风压分布未受到较大影响,分布特性和数值大小均与并列工况相似,背风楼由于主要受到前方建筑遮挡,迎风面处于迎风楼尾部的回流区中,减弱了来流的撞击作用,使得正压变小;同时,背风楼侧面的分离作用也会减弱,与并列工况下相比,负压也会变小.
数值模拟的结果能较为准确地反映出结构表面风压分布趋势,可提供前期抗风设计的依据.虽然,现阶段CFD方法还不能完全取代风洞试验,但是随着计算机技术的发展与湍流模型的改进,该方法在结构抗风设计研究中的作用将会越来越大.
[1] 沈世钊, 武岳.大跨度张拉结构风致动力响应研究进展[J]. 同济大学学报(自然科学版),2002,30(5):533-538.
[2] 顾明, 黄鹏. 群体高层建筑风荷载干扰的研究现状及展望[J]. 同济大学学报(自然科学版), 2003, 31(7): 762-766.
[3] 李秋胜, 郅伦海, 段永定, 等. 台北101大楼风致响应实测及分析[J]. 建筑结构学报, 2010, 31(3): 24-31.
[4] 雷静雅, 徐兵先, 马守龙, 等. 典型超高层建筑风荷载的风洞试验研究[J]. 武汉理工大学学报, 2013, 35(1): 94-98.
[5] 冯永伟, 吴小平, 杨学林, 等. 基于风洞试验的双塔楼超高层建筑风荷载与风致响应[J]. 建筑结构, 2012, 42(8): 65-68.
[6] 秦云, 张耀春, 王春刚. 数值风洞模拟结构静力风荷载的可行性研究[J]. 哈尔滨工业大学学报, 2004, 36(12): 1 593-1 597.
[7] 张敏, 楼文娟, 何鸽俊, 等. 群体高层建筑风荷载干扰效应的数值研究[J]. 工程力学, 2008, 25(1): 179-185.
[8] 卢春玲, 李秋胜, 黄生洪, 等. 深圳平安国际金融大厦风致响应大涡模拟分析[J]. 建筑结构学报, 2012,33(11): 1-11.
[9] 谢华平, 陈俊, 尹志明. 输电塔风振系数分析[J]. 湘潭大学自然科学学报, 2013, 35(3): 40-44.
[10] 张德生, 李远瑛. 拱型波纹屋盖结构风致振动数值模拟研究[J]. 湘潭大学自然科学学报, 2014, 36(3):41-46.
[11] CARDOT B, CORON E, MOHAMMADI B. Simulation of turbulence with thek-εmodel[J]. Computer Methods in Applied Mechanics and Engineering, 1991, 87(2-3): 103-116.
[12] 黄本才. 结构抗风分析原理及应用[M]. 2版.上海: 同济大学出版社, 2008.
[13] 建筑结构荷载规范:GB50009-2012[S]. 北京: 中国建筑工业出版社, 2012.
责任编辑:罗 联
Study on Interference Effects of Wind Loads of a Multi-Tower Tall Building
TUJia-huang1*,LIANGJing-qun2,HUANGCheng3,SHIXiao-dong1,YANGLei4,WANGChun-lei3,ZHANGTing-ting3
(1.College of Civil Engineering and Mechanics, Xiangtan University, Xiangtan 411105;2.Department of Manage Students of Xiangtan University, Xiangtan 411105;3.Beijing Institute of Architectural Design, Beijing 100045;4.Beijing Glory Real Estate Development Co.ltd, Beijing 100050 China)
Based on the project of Ordos Guo Tai Business Plaza, the wind field around the multi-tower tall building is simulated by Reynolds-Averaged Navier-Stokes method and standardk-εturbulent model, while the wind loading shape coefficient distribution of structural surface at different wind angles is obtained. Then, the characteristics of wind field under different arrangement cases are analyzed and the mechanism of interference effects between towers is revealed. Compared with the data obtained from wind tunnel test, it shows that the computational results could accurately obtain the pressure distribution of the multi-tower tall building, providing a reference for wind-resistant design of such building.
multi-tower tall building; interference effect; shape coefficient; wind load
2015-01-16
湘潭大学科研启动费资助项目(13KZ|KZ08025)
涂佳黄(1982— ),男,湖南 益阳人,博士,讲师.E-mail:tujiahuang1982@163.com
TU312.1
A
1000-5900(2015)02-0038-07

