基于经验模态分解结合傅氏变换与Wigner分布的Mel频率倒谱系数提取*

曾以成， 陈雨莺， 毛燕湖， 谢小娟

(湘潭大学 物理与光电工程学院，湖南 湘潭 411105)

基于经验模态分解结合傅氏变换与Wigner分布的Mel频率倒谱系数提取*

曾以成*， 陈雨莺， 毛燕湖， 谢小娟

(湘潭大学 物理与光电工程学院，湖南 湘潭 411105)

根据语音信号的非平稳特点，用经验模态分解方法把语音信号分解成一系列固有模态函数(Intrinsic Mode Function，IMF)，一个IMF只含有语音信号的一部分信息，不同IMF分量携带的特征信息不同，对这些IMFs进行加权处理，得到新的语音，再对其进行后续处理.Wigner-Ville分布能精确地定位信号的时频结构，而传统傅氏变换不能反映信号的瞬时变化情况，但多分量信号的Wigner-Ville分布受困于交叉项的干扰，因此利用Wigner-Ville分布的优点，采用Wigner-Ville谱与傅氏谱结合来代替单独的傅氏谱作为每帧的特征，进行Mel频率倒谱系数(Mel Frequency Cepstrum Coefficient，MFCC)提取.实验表明，经改进后的MFCC参数较传统的MFCC参数应用于说话人识别系统，识别率有较大提升，且鲁棒性较好.

经验模态分解；Wigner-Ville谱；傅氏变换；Mel频率倒谱系数

语音信号是复杂的非平稳信号，但短时平稳，包含语义、个人特征、情感等特征信息，不同特征信息需用不同的特征参数表征，所以，特征参数的提取是语音信号处理的一个关键步骤.常见的反映个性特征信息的特征参数有：基音周期、线性预测参数、线谱对参数(Line Spectrum Pair，LSP)、梅尔频率倒谱系数(Mel Frequency Cepstrum Coefficient，MFCC)以及口音敏感参数(Accent Sensitive Cepstrum Coefficient，ASCC)等.MFCC考虑了人耳的听觉特性，将频谱转化为基于Mel频率的非线性频谱，然后转换到倒谱域上.因没有任何前提假设，MFCC参数具有良好的识别性能和抗噪能力.

为进一步提高说话人识别系统的识别率，很多学者尝试对MFCC进行改进[1～7].比如，文献[3]考虑到Mel频率倒谱系数中各维分量对于不同说话人的区分程度，采用加权的办法进行矢量量化，使特征参数能够更好地区分不同说话人，但文中加权系数的选择还有待研究.文献[4]提出基于概率加权平均的Mel子带特征重建算法，减少了帧间突变现象，增强了Mel子带特征的帧间连续性，但重建误差仍然会影响语音识别系统性能的提高.文献[5]将感知加权技术应用到Mel倒谱分析中，通过对基于心理声学模型计算得到的信号掩蔽比差值获得感知权重函数，而其中误差函数的最小化问题，对识别性能有一定的影响.文献[6]将语音频谱能量高频部分进行加权来提取MFCC参数，这种方法可使语音增强，提高语音鲁棒性，但对于高频与低频怎么区分却是一个问题.这些改进方法使得说话人识别率有所提升，但提升的高度还有待进一步增加.

Wigner-Ville分布[8，9]适合于非平稳信号的分析与处理.它具有比其他时频分布更好的时频聚集性，能够很好地区分一个信号是单分量信号还是多分量信号，在识别信号项的情况下，还可以知道信号的组成频率随时间的变化规律，这与传统的傅氏分析法相比具有一定的优越性，因为傅氏变换不具有时间和频率的“定位”功能，不能反映信号的瞬时变化情况.

基于上述考虑，本文提出一种基于经验模态分解(Empirical Mode Decomposition，EMD)[10，11]结合傅氏变换与Wigner分布的MFCC特征提取算法.首先，应用EMD分解法处理语音信号，其次，将Wigner-Ville(WV)谱和傅氏谱结合，经过Mel滤波器组，进行离散余弦变换，提取说话人的MFCC特征参数，最后采用高斯混合模型(GMM)实现说话人识别.

1 原理及其算法

EMD是一种新的应用于非线性与非平稳时间序列信号的分解方法，其核心是：把任意一个复杂信号分解成一系列不同尺度的固有模态函数(Intrinsic Mode Function，IMF)和一个残余分量，每一个IMF代表了原信号不同频率段的振荡变化，突出信号的局部特征，残余分量则体现信号中的缓慢变化量[12,13].

先将语音信号分帧(每帧10～30 ms)，一帧期间内的信号视为平稳过程，将整帧信号作离散傅里叶变换(Discrete Fourier Transform，DFT)等处理得到该帧信号的频谱或者功率谱特性.这种处理方法遇到的问题是帧长的选取是否合宜，若选得太长，在语音信号的特性时变明显的情况下，帧会将不同时刻具有相当特性差别的特征彼此混淆，或将一些短时出现的重要特征冲淡.反之，若帧长取太短，则会因帧内样本数少而不足以表征低频成分，这相当于加上了使信号畸变的低通滤波.解决这个问题的途径之一是将帧长取得较长，采用高阶信号谱来代替傅里叶谱，使之能较好地表征时变信号的特性.而WV谱就是一种高阶信号谱，离散WV谱的定义是：

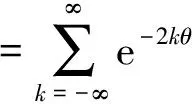
(1)

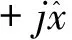
由W(n,θ)的定义式可见，W(n,θ)实际就是xA(n+k)·xA*(n-k)的傅里叶变换，也即xA(n)的一种自协方差的傅里叶变换，与信号本身的傅里叶谱相比，对于非平稳信号，在较长帧长情况下，信号傅里叶谱特征的表征性能已有所下降，而WV谱只要该信号的自协方差还接近平稳，它的表征性能还是很好的[16].

2 基于EMD结合傅氏变换与Wigner分布的MFCC特征提取过程

语音信号经过EMD分解后，得到的每一级IMF中所包含的信息量是不同的，这里，我们根据每个IMF序列与原始序列的相关性，来衡量一个IMF的信息量.而相关性由相关系数r来描述，r的表达式如下：

(2)

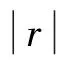
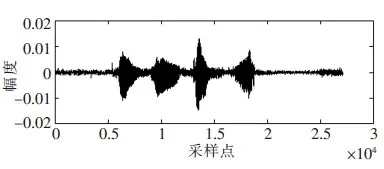
图1 原始语音信号
Fig.1 The original speech signal

以“同舟共济”这个词组的普通话汉语语音为例(采样频率为8 000Hz)，波形如图1所示.取其中400个采样点(从6001点到6400点)进行EMD分解，得到一组IMF，如图2所示.由图可见，这段语音信号分解出5个IMF和1个残差序列.

图2 EMD 分解后的IMF 分量集，从上到下依次为IMF1~IMF5与残差
Fig.2 IMF components obtained by EMD method, and from top to bottom are IMF1to IMF5and the residual

由图2可以看出，分解后得到的第一个固有模态函数IMF1，极大值、极小值点最多，之后的IMF随着极大值、极小值点的减少而依次变得平坦.所以，设语音信号x(t)，经过EMD分解后得到n个IMF，对其进行加权[17，18]，数学表达式为：

(3)

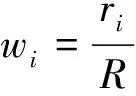
图3 原始信号与IMF 加权后的信号对比(200 个采样点)
Fig.3 Contrast the original signal with the weighted signal (200 sampling points)

由图3可以看出，进行加权处理后，得到的新信号的幅度明显变小了，这是因为一部分不相关的信息被筛除了，保留的是我们需要的相关信息，相当于为进行特征参数提取对原始语音进行了“优化”.

我们对加权后得到的新信号分别作WV运算和快速傅里叶变换(FastFourierTransformation，FFT).

若信号x(n)=x1(n)+x2(n)，则它的WV分布为：

Wx(n,ω)=Wx1(n,ω)+Wx2(n,ω)+2Re[Wx1,x2(n,ω)]，

(4)

式中：2Re[Wx1,x2(n,ω)]是x1(n)和x2(n)的互Wigner分布，称为交叉项，这是信号叠加产生的干扰.由此看出，两个信号和的Wigner分布并不等于它们各自Wigner分布的和.当信号由很多分量叠加组成时，交叉项会严重到无法区分信号项和交叉项.

对于FFT，它是线性变换，不存在交叉项，但其时频聚集性不好；对于WV分布，它具有很好的时频聚集性，但存在严重的交叉项.本文结合两者的优点，得到既不含交叉项且时频聚集性又好的新分布.

当信号分别作FFT和WV处理后，即得到Fx(n,ω)和Wx(n,ω)，对二者进行相乘运算，当两者都有信号项时，可以得到乘积结果，而WV的交叉项对应的FFT区域没有信号，所以乘积为0.通过这种算法，实现一个表征性能更优的分布[19，20].

进行FFT与WV相乘运算后，再经过Mel滤波器组，作离散余弦变换(DiscreteCosineTransform，DCT)，得到MFCC.具体的MFCC参数提取流程如图4所示.

3 实验结果与分析

实验采用10个人的汉语语音库，其中5名男性，5名女性，采样频率为16 kHz.我们对原始语音进行预加重，然后分帧去静音(采用短时平均能量作为判断标志)，得到处理后的语音.将处理后的语音作为流程图中的语音信号，按上述步骤进行分析处理.

在上述流程图中，若去掉分解步骤，则得到的参数定义为WV-FFT的MFCC参数；若去掉相乘步骤，则得到的参数定义为IMF加权的MFCC参数；若进行完整的流程图运算，则得到的参数定义为WV-IMF的MFCC参数.

将这三种参数与传统的MFCC参数作比较，进行说话人识别测试.在理想情形下，测试结果如表1所示.

表1 理想情形下四种方法的识别结果

由表1可以看出，经本文改进后的MFCC参数的识别率相比传统的MFCC参数，有大幅度提升.WV-FFT的MFCC参数与IMF加权的MFCC参数的识别率提高了大约10%，而WV-IMF的MFCC参数的识别率最高，比传统MFCC参数的识别率高出了15%左右，这说明本文提出的方法具有更好的识别效果.

然而，在现实生活中，语音信号不可能是纯净的，我们在原始语音中加入随机噪声(高斯白噪声)，对比这些参数在不同信噪比下的说话人识别率.测试结果如表2所示.

比较表2中的结果可知，加入噪声后，在高信噪比下，经本文改进过的MFCC参数的识别率都有提升，提升幅度最大的是WV-IMF的MFCC.随着信噪比的降低，WV-FFT的MFCC参数的识别率迅速下降，IMF加权的MFCC参数次之，而WV-IMF的MFCC参数的识别率下降是最缓慢的，所以低信噪比下，WV-IMF的MFCC识别率最好.

表2 高斯白噪声下不同信噪比的识别结果

噪声也可以分为很多种，在加入不同种类的噪声情况下，识别率也有所不同.这里，我们选择标准噪声库NoiseX-92中比较常见的三种噪声来作比较实验，分别是潺潺的发言声、粉红噪声(自然界最常见的噪声)和工厂噪声，将它们分别加入语音信号，信噪比定为30 dB，再来比较说话人识别率.测试结果如表3所示.

表3 不同噪声下同一信噪比的识别结果

由表3可知，对于传统的MFCC参数，在潺潺的发言声环境下识别率相对较好，而改进后的三种MFCC参数，在粉红噪声环境下说话人识别率相对较高.其中，WV-IMF的MFCC参数的识别率最高，相对于传统的MFCC参数，有最大幅度的提升；潺潺的发言声环境下，IMF加权的MFCC参数和WV-IMF的MFCC参数的识别率相差不大，WV-IMF的MFCC参数的识别率略高于IMF加权的MFCC参数的识别率；工厂噪声环境下，识别率相对较低，但是，WV-IMF的MFCC参数的识别率仍然高于其他MFCC参数.整体来看，噪声环境下，WV-IMF的MFCC的识别率最好.

4 结束语

本文提出了一种基于EMD结合傅氏变换和Wigner分布的MFCC特征提取方法.首先，利用EMD分解出的IMF与原始信号的相关性来筛去部分无用信息，这一步骤相当于为MFCC的提取对原始语音进行了“优化”，而结合FFT与Wigner分布的方法在去掉交叉项的同时保留了良好的时频分辨率.实验表明，本文方法较传统的MFCC参数提取法，说话人识别率有一定提高.在理想情况下，本文方法得到的识别率高出传统MFCC参数提取法将近15%；在高斯白噪声环境下，识别率都有所下降，但是本文方法仍然高出传统MFCC参数提取法10%以上；在潺潺的发言环境下，本文方法的识别率提高了14%左右，在粉红噪声、工厂噪声这两种特殊噪声情形下，本文方法的识别率提高了24%左右.但信噪比较低的时候(信噪比20 dB以下)，说话人识别系统的识别率比较低，所以如何提高低信噪比下的说话人识别率还需要进一步研究.

[1] 鲜晓东,樊宇星. 基于Fisher比的梅尔倒谱系数混合特征提取方法[J].计算机应用，2014,34(2):558-561,579.

[2] 俸云,景新幸,叶懋. MFCC特征改进算法在语音识别中的应用[J].计算机工程与科学，2009,31(12):146-148.

[3] 邵央,刘丙哲,李宗葛. 基于MFCC和加权矢量量化的说话人识别系统[J].计算机工程与应用，2002,38(5):127-128.

[4] 罗宇,杜利民. 基于概率加权平均的Mel子带特征重建算法[J].电子学报，2004,32(10):1 738-1 741.

[5] 刘亚丽,杨鸿武,黄德智. 基于加权Mel倒谱系数的说话人识别[J].计算机应用与软件，2009,26(9):24-27.

[6] 陈迪,龚卫国,李波. 噪声鲁棒性说话人识别语音高频加权MFCC提取[J].仪器仪表学报，2008,29(3):668-672.

[7] 汤霖,彭土有,尹俊勋.普通话水平客观测试中的韵母测试研究[J].湘潭大学自然科学学报,2012,34(1):95-100.

[8] QIAN S, MORRIS J M. Wigner distribution decomposition and cross-terms delete representation[J].Signal Processing,1992,27:125-144.

[9] WONG K M, JIN Q. Estimation of the time-varying frequency of a signal: The cramer-ral bound and the application of Wigner distribution[J]. IEEE Trans Signal Processing, 1990,1 770:358-375.

[10] HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-station time series analysis[J].The Royal Society,1998,A454:903-995.

[11] HUANG N E,WU M L, QU W, et al. Applications of Hilbert-Huang transform to nonstationary financial time series analysis[J].Applied Stochastic Models in Business and Industry,2003,19:245-268.

[12] YANG Z H, QI D X,YANG L H. A novel approach for detecting pitch based on Hilbert-Huang Transform[R]. Sun Yat-sen University, 2004.

[13] YAN R Q， GAO R X. A tour of the Hilbert-Huang transform: an empirical tool for signal analysis[J]. IEEE Instrumentation & Measurement Magazine,2007,10(5):40-45.

[14] 杜晓青,于凤芹. 基于HHT倒谱系数的说话人识别算法[J].计算机工程与应用,2014(3):198- 202.

[15] 刘丽伟,张瑶,赵孔新,等. 基于HHT的语音特征参数提取及其在说话人识别中的应用[J].长春工业大学学报(自然科学版),2009,30(6):696- 701.

[16] 王炳锡，屈丹，彭煊. 实用语音识别基础[M].北京：国防工业出版社,2005:66-74.

[17] 李凌,曾以成,雷雄国.EMD在说话人辨认中的应用[J].湘潭大学自然科学学报,2006,28(3):108-111.

[18] 孙汝儒,肖迪. 基于加权IMF对时间序列相似匹配[J].计算机应用研究,2013,30(12):3 664-3 666.

[19] 赵淑红. 短时傅立叶变换与Wigner-Ville分布联合确定地震信号瞬时频率[J].西安科技大学学报,2010,30(4):447-450.

[20] 吴小羊，刘天佑. 基于时频重排的地震信号Wigner-Ville分布时频分析[J].石油地球物理勘探,2009,44(2):201-205.

责任编辑：罗 联

Mel Frequency Cepstrum Coefficient Extraction Method Based on Empirical Mode Decomposition and Combined Spectrum of Fourier Transform and Wigner Distribution

ZENGYi-cheng*,CHENYu-ying,MAOYan-hu,XIEXiao-juan

(Department of Physics and Photoelectric Engineering, Xiangtan University, Xiangtan 411105 China)

Speech signal has the non-stationary and nonlinear characteristics, and is decomposed into a number of intrinsic mode functions by applying Empirical Mode Decomposition method. Each IMF contains only part of the information of the speech signal, and different characteristic information carried by different IMF component. Then these IMFs are weighted to get a new speech signal for further processing. Wigner-Ville Distribution can accurately reflect the time-frequency structure of the signal. On the contrary, the Fourier transform can not reflect the instantaneous change of signal. But Wigner-Ville Distribution trapped in cross-term interference by multi-component signals generated. Take advantage of Wigner-Ville Distribution, and using Wigner-Ville spectrum and Fourier spectrum combine to replace Fourier spectrum as the characteristic of each frame for extracting Mel Frequency Cepstrum Coefficient (MFCC). Experiments show that in speaker recognition system, compared with the classical MFCC parameter, the improved MFCC parameter in this article provides a higher accuracy and better robustness.

Empirical Mode Decomposition(EMD); Wigner-Ville spectrum; Fourier transform; Mel Frequency Cepstrum Coefficient(MFCC)

2005-01-06

曾以成(1962— )， 男，湖南 涟源人，博士，教授，博士生导师.E-mail:yichengz@xtu.edu.cn

TP391

A

1000-5900(2015)02-0020-07