HHT在遥测信号处理中的应用
师培峰,邱 伟,吴瑞斌,王晓斌
(北京强度环境研究所 北京 100076)
引言
在各类飞行试验中,遥测数据为制定飞行器环境试验条件、检验系统工作性能和故障定位提供了重要依据,对遥测数据进行准确、有效处理[1]具有极其重要的意义。由于飞行环境、电磁干扰及传感器零位漂移等原因,遥测数据往往存在虚假趋势,并混杂有周期性干扰和噪声干扰。为改善数据品质,需要对数据进行预处理。此外,由于遥测数据具有非线性、非平稳(时变)的特点,基于傅里叶变换的传统频域分析方法往往无法表述信号的时频局部特征,而这种性质恰恰是非平稳信号[2]最根本和最关键的性质。基于HHT[3](Hilbert-Huang Transform)技术的遥测信号处理方法,可以有效完成信号预处理和时频分析,为高效处理遥测数据提供了有力工具。
1 HHT基本理论
HHT利用经验模态分解[4](EMD)将信号自适应分解为一系列的固有模态函数(IMF)信号分量,对每个IMF信号进行Hilbert变换得到信号的瞬时频率和每个IMF信号分量的时频序列。在HHT理论中,IMF信号分量满足以下条件:
①整个数据序列中,极值点的数量与过零点的数量相等或至多差一个;
②信号上任意一点,由局部极大值点确定的包络线和局部极小值点确定的包络线的均值为零,即信号关于时间轴对称。
IMF信号分量通过EMD计算得到。与经典的Fourier变换理论中有关信号的基本组成分量不同,EMD方法认为非线性、非平稳信号的基本组成分量不是正余弦信号,而是IMF信号分量。EMD是以IMF为基函数的时域分解方法。采用EMD方法分解任意一个信号s(t)的具体步骤有如下七步。
①提取信号s(t)的所有极大值和极小值极点;
②利用三次样条函数分别基于所有极大值点与极小值点拟合信号s(t)的上包络和下包络,并用它们近似地表示信号s(t)真实的上、下包络线;
③求上包络和下包络的均值m1(t),作为信号s(t)的真实均值包络曲线;
④用信号s(t)减去均值包络m1(t)得到新的信号h1(t),即

⑤将h1(t)视为新的s(t),对h1(t)重复步骤①~④。假设通过k次迭代(k≥2)得到满足IMF信号分量两个条件的h1k(t),则h1k(t)是第一个IMF信号分量,即

用字符C(t)表示IMF信号分量,Ci(t)表示第i个IMF信号分量,令

则C1(t)就是信号s(t)的第一个IMF信号分量,它包含了原始信号里最高频部分的信号。
⑥用原始信号减去第一个IMF信号分量,得到第一个残余信号R1(t),即

⑦对第一个残余信号R1(t)重复步骤①~⑥,可以得到每个IMF信号分量Ci(t)及残余信号Ri(t),即
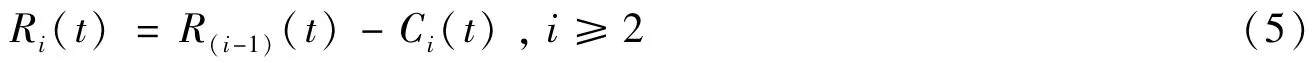
若残余信号Ri(t)满足:Ri(t)或Ci(t)小于设定的误差或者Ri(t)为单调函数,则EMD分解终止。
在实际的数据处理过程中,步骤⑤中迭代次数k的值通过迭代阈值(标记为SD)来确定,SD的计算如式(6)所示。实践表明,SD的取值在0.2~0.3之间为宜,既可保证IMF信号分量的线性和稳定性,又可使IMF信号分量具有相应的物理意义[5]。
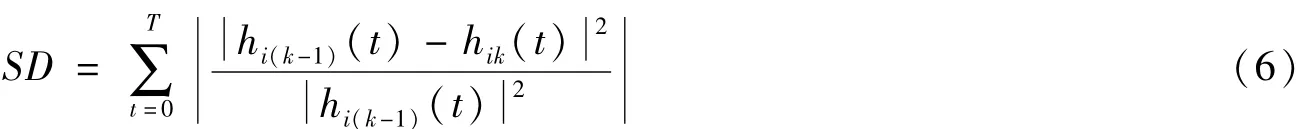
式(6)中,t为信号采样时刻点,T为总采样时间。
原始信号s(t)通过EMD分解得到n个IMF信号分量(C1(t),…,Cn(t))和残余信号Rn(t),根据EMD方法原理可知

所有的IMF信号分量包含了原始信号中频率由高到低的部分。每次EMD分解产生的IMF信号的频率是逐次降低的。
对单个IMF信号分量Ci(t)进行HT(Hilbert变换),可以得到Ci(t)的解析信号,即
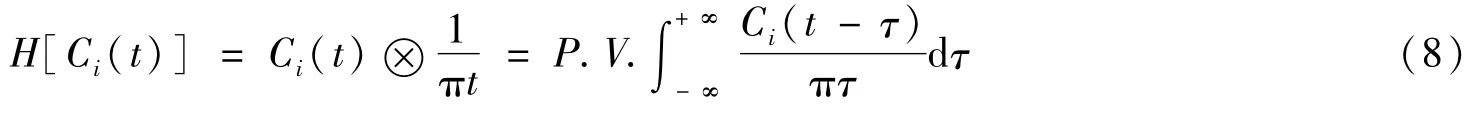
其中P.V.表示柯西主值积分。构造Ci(t)的解析函数为
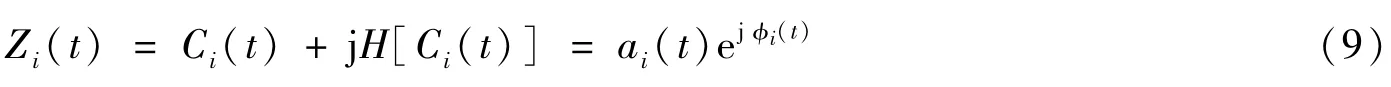
其中幅值函数和相位函数分别为

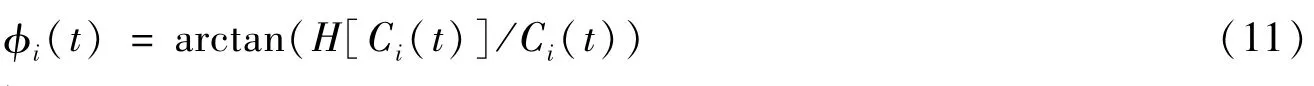
在式(11)的基础上定义瞬时频率为

从式(12)可以看出,HT变换后的瞬时频率是时间的函数,能够对任意信号任意时刻频率变化进行分析和度量,尤其是非平稳信号。通过对每个IMF信号分量进行HT变换,就可以得到每个IMF信号分量的频率随时间的变化曲线。
2 基于HHT的信号处理
在对遥测信号进行数据分析之前,需要对信号进行预处理。遥测信号的预处理主要包括信号虚假趋势项排除[6]和信号去噪[7,8]两方面的工作。
2.1 趋势项排除
目前趋势项排除的主要方法有:①高通滤波[9],滤波截止频率应小于下限分析频率的1/2;②最小二乘多项式拟合,提取出趋势项信号的多项式;③滑动平均,根据趋势项特征选择阶次;④小波分析[10],利用小波分解去除趋势项后进行波形重构。上述四种方法都有特定的使用条件:①高通滤波的性能与阻带衰减特性、通带平坦度、窗类型及阶数有关;②最小二乘多项式拟合的阶数受到限制,而且高阶多项式的拟合效果也不理想,需谨慎使用。③滑动平均的趋势提取效果与点数相关,采用不同点数进行滑动平均差异较大;④小波分析往往需要选择合适的小波类型和分解层数,才能取得较好的效果。这四种方法要选择合适的参数类型往往比较困难,而且针对特定的数据才有较好的趋势提取与排除效果。本文基于HHT理论,对遥测信号进行EMD分解,得到从高频到低频有序排列的多个IMF信号分量。这本质上是一个从高频到低频的多分辨率自适应滤波[11]过程,分解过程中不存在信号失真问题,具有完备性和可重构性。通过对高频IMF信号分量线性叠加进行信号重构,实现低频趋势项排除。图1为一实测遥测振动信号时间历程图(g=9.8m/s2),通过EMD分解得到11个相互正交的IMF信号分量,分别记为imf-1、…imf-11,如图2和图3所示(t表示time,a表示acceleration)。
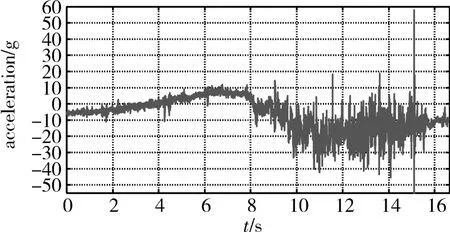
图1 实测遥测振动信号时间历程图Fig.1 Time-domain curve of telemetry vibration signal
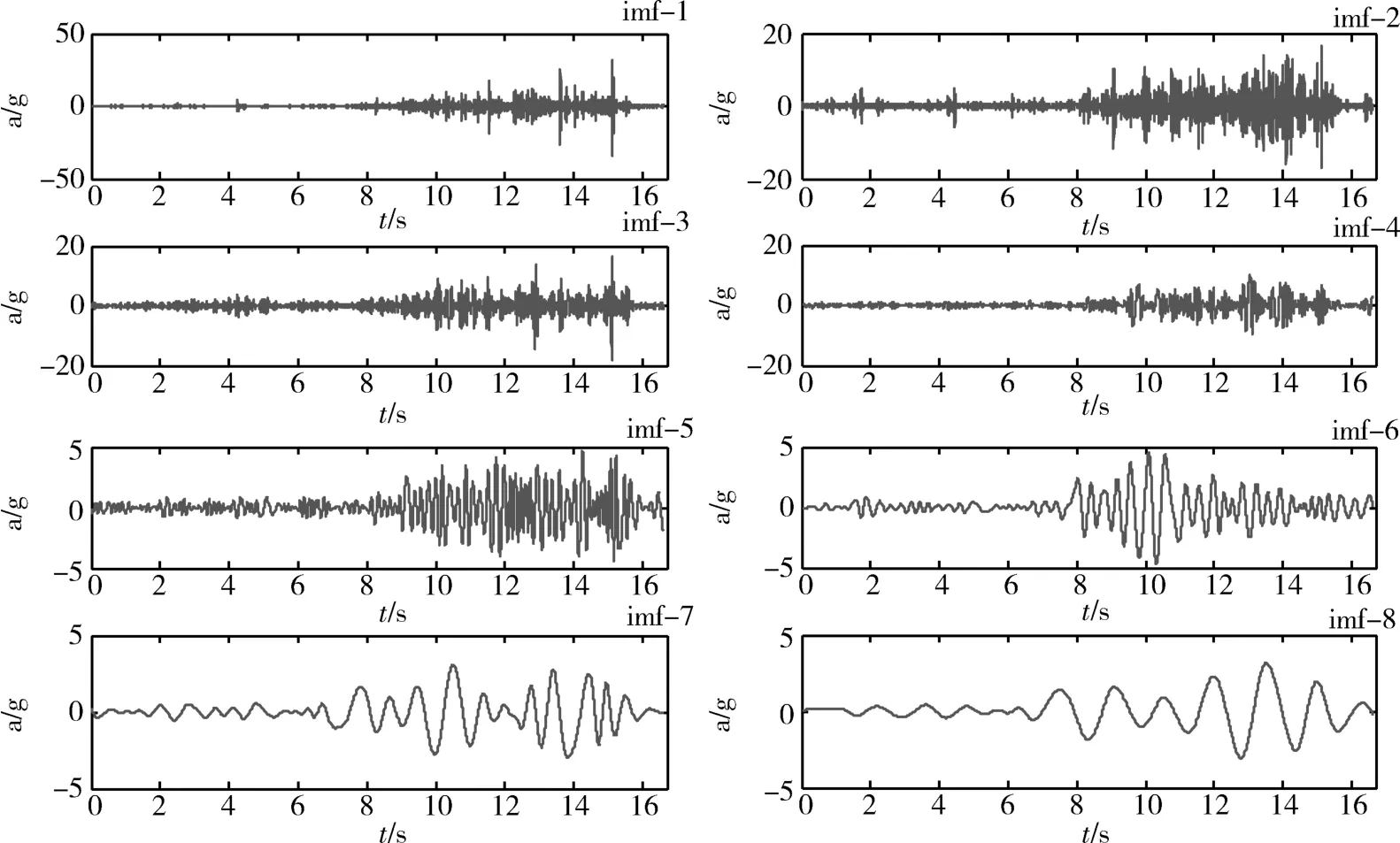
图2 EMD分解后的前8组IMF信号Fig.2 The former 8 IMF signals by EMD decomposition
根据式(7),由EMD分解后的前8个IMF信号得到重构后的信号,即排除了趋势项后的数据。分别采用本文方法、高通滤波法和小波变换法进行趋势项排除,结果对比如图4所示。
从图4中可以看出,从排除趋势项的效果来看,对于初始值不在零线的数据,采用高通滤波法在初始位置会出现扰动,而且人为设置高通截止频率具有较大的随意性;小波变换方法和本文方法都能够有效去除趋势项,但小波变换法处理后数据的加速度均方根(RMS)值为4.23g,本文方法处理后数据的RMS值为4.92g,由于小波方法中小波基的选择依据个人经验,因此在排除趋势项的过程中,会丢失部分真实的高频趋势项数据信息,而本文方法通过自适应分解实现,在排除虚假趋势项的同时保留了真实的高频细节趋势项数据,更真实地反映了遥测振动的物理过程。
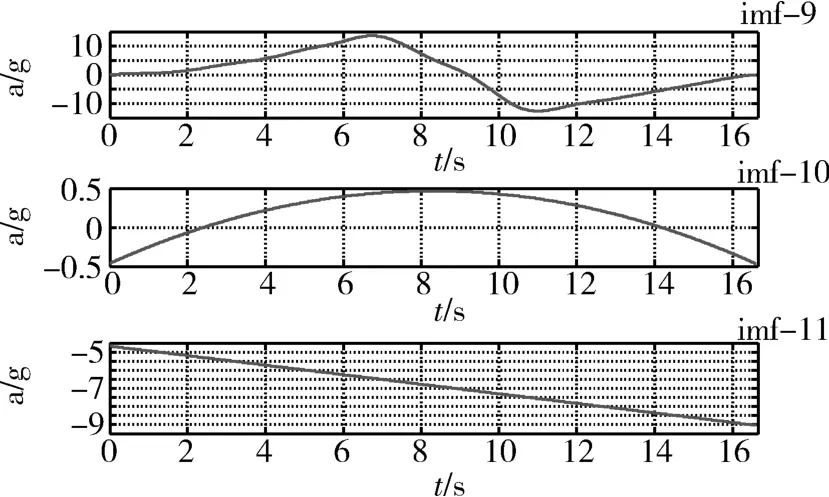
图3 EMD分解后具有趋势项的后3组IMF信号Fig.3 The later 3 IMF signals containing trend by EMD decomposition

图4 三种方法排除趋势项效果对比Fig.4 Trend extraction and elimination contrast of three methods
2.2 去噪滤波
在飞行遥测试验中,由于工频、帧码、采样频率和弹上记录校准信号的干扰和影响,许多遥测数据存在某些频率及其谐波的干扰周期分量,尤其是在低频参数中,因此必须抑制干扰频率及其谐波频率的影响。目前抑制工频及其谐波干扰的方法主要是设计带阻滤波器和小波变换分析方法降噪。滤波器法是使信号幅值在需要消除的干扰频率点上为零。由于干扰频率往往是一个点频率,加上滤波器的过渡带衰减、通带波动、相位延迟等特性的影响,滤波器法在实际操作中比较复杂,而且很难消除工频及其谐波频率的干扰。小波变换作为一种信号去噪方法,其基本思想是首先寻找一个满足一定条件的母波函数,然后通过母波函数的平移和伸缩构成小波基,再利用小波基去逼近所要研究的信号,进行时频局部分析,从而达到去噪的目的。小波变换也具有多分辨特性,但小波变换本质上是一种窗口可调的傅里叶变换,没有从根本上摆脱傅里叶分析的局限。与上述两种方法不同的是,经EMD分解后的IMF信号分量都是平稳的,由于EMD分解是从信号本身的特征时间尺度出发对信号进行分解,没有固定的先验基底,是自适应的[11],因此得到的IMF信号分量具有明显的物理意义,表现了信号的真实物理过程。本文基于HHT原理,通过以下四步骤实现滤波去噪:
①对原始信号s(t)进行EMD分解,得到M个IMF信号分量,记为IMFsi(t),i=1…M。
②对第i个IMF信号分量IMFsi(t)进行HT变换,得到IMFsi(t)的时间-频率曲线,记为Fi(t)。
③从Fi(t)中标记出第i个IMF信号分量的干扰频率及其谐波频率,将Fi(t)中其他频率对应的IMF信号分量序列标记为IMF(1)si(t),i=1…N,N<M。
④去除干扰频率后的信号s(t)通过IMF(1)si(t)实现信号重构,即

通过叠加不同的IMF(1)si(t)信号分量,可以得到所需类型的滤波器(低通、高通、带通、带阻等),从而实现对遥测信号的自适应滤波和去噪分析。以实测信号为例,信号采样频率为1024Hz,信号成分主要是40Hz以内的低频部分,在采集过程中有较大的背景噪声,并夹杂有50Hz及其倍频谐波的干扰。时域波形及频谱分析如图5所示。
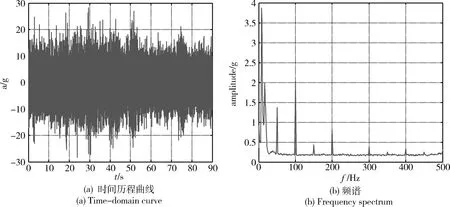
图5 遥测振动信号时间历程及频谱Fig.5 Time-domain curve and frequency spectrum of telemetry vibration signal
对图5(a)所示的实测遥测振动信号进行谱分析,得到频谱图,如图5(b)所示。从图5(b)中可以看出,振动信号中夹杂着50Hz及其倍频谐波的干扰。分别采用数字滤波器法、小波变换法和本文方法进行滤波去噪处理,并分两种情况进行讨论。
①只保留40Hz以内频带的信号。
三种方法滤波去噪效果如图6所示。

图6 保留40Hz以内频带信号频谱Fig.6 Frequency spectrum by keeping the signal within 40Hz
②只消除50Hz及其倍频谐波的干扰。
三种方法滤波去噪效果如图7所示,局部细节如图8(a)、8(b)所示。
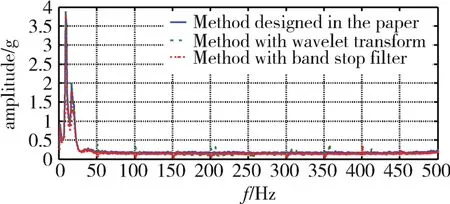
图7 去除50Hz及谐波干扰后的信号频谱Fig.7 Frequency spectrum after eliminating the interference of 50Hz and its harmonic frequency
从图6对比结果可以看出,本文方法能够有效消除频率大于40Hz的信号。IIR滤波器由于过渡带衰减斜率的影响,无法完全消除50Hz工频信号的干扰。小波变换方法由于小波基不是自适应的,也无法完全消除50Hz及其谐波信号的干扰。
从图7和图8对比结果可以看出:采用带阻滤波器方法,在50Hz及其谐波频率处出现局部信号失真,表现为50Hz及其谐波频率处频谱出现谷值,而且主频范围(40Hz以内)内信号幅值明显降低,说明有效信号的部分信息丢失;小波分析方法与本文方法的频谱图在主频范围内保持较好的一致性,但是小波分析方法无法完全消除50Hz及其谐波频率信号的干扰,而本文方法在消除50Hz及其谐波频率干扰的同时,保证了主频范围内信号不丢失。
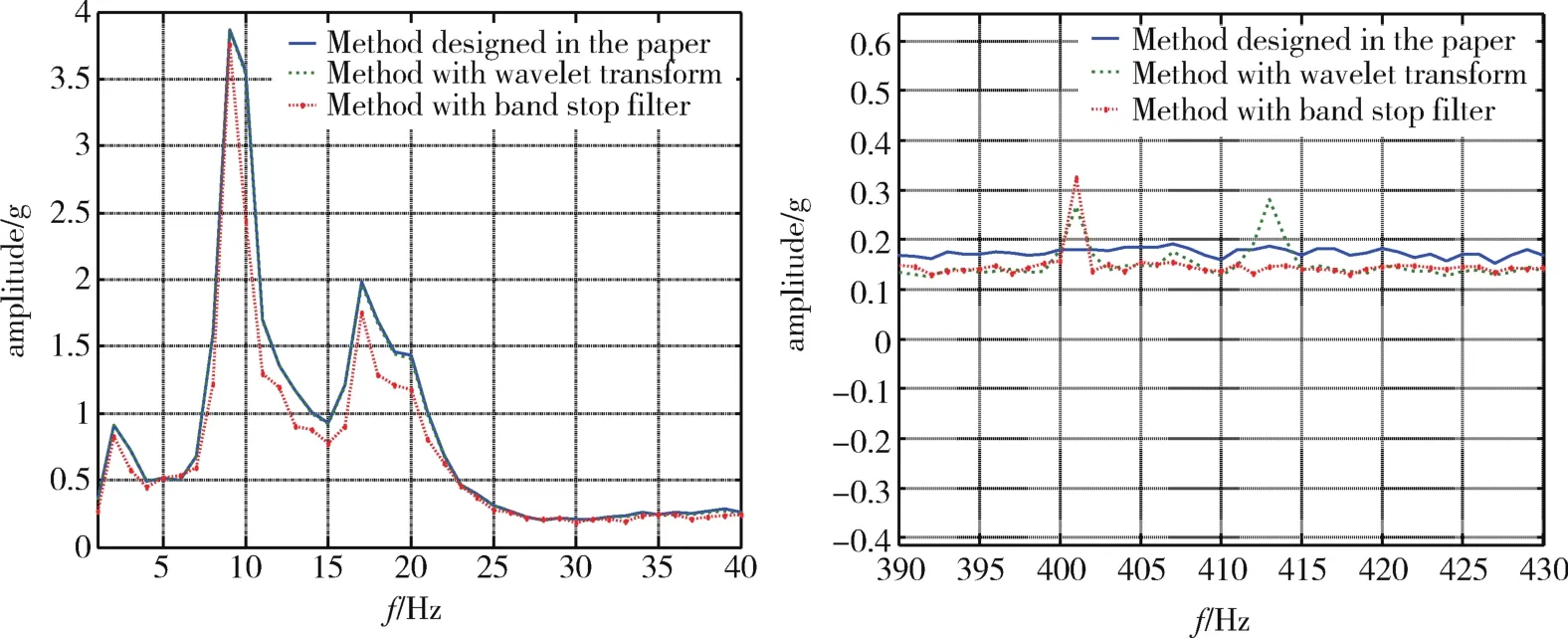
图8 局部细节展开图Fig.8 Curve details of figure 7
3 结束语
本文研究了HHT在遥测信号处理中的应用。仿真实验结果表明,基于HHT的数据处理技术可以自适应对信号进行分解,它结合了EMD分解和IMF信号分量的特性,有效地实现了信号趋势项提取和排除以及自适应信号滤波降噪处理。本文方法应用前景广阔,可为各种信号的数据处理提供一种新的有力工具。
[1]陈以恩,等.遥测数据处理[M].北京:北京国防工业出版社,2002.
[2]科恩 L.时-频分析:理论与应用[M].白居宪,译.西安:西安交通大学出版社,2000:22~40.
[3]Huang N E,Shen Z,Long SR,et al.The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non stationary Time Series and Analysis[J].Pro.Roy.Soc.London.A,1998,454:903 ~995.
[4]Peng Z K,Tse PeterW,Chu F L.An Improved Hilbert-Huang Transform and Its Applicaition in Bibration Signal Analysis[J].Journal of Sound and Vibration,2005,286:187 ~205
[5]Rilling G,Flandrin P.On Empirical Mode Decomposition and Its Algorithm[C]//IEEE-ERUASIP Workshop on Nonlinear Signal Image Processing.NSIP-03,Gradp(I),June 2003.
[6]陈 燕,刘 哲,郑 宾.基于LabVIEW的测试信号预处理方法研究[J].国外电子测量技术,2008,27(10):4~5,16.Chen Yan,Liu Zhe,Zheng Bin.Study on Test Signal Pre-processing Method Based on LabVIEW[J].Foreign Electronic Measurement Technology,2008,27(10):4~5,16.
[7]肖方煜,汤 伟,傅 娜.自寻优阈值小波去噪方法[J].信号处理,2012,28(4):577~586.Xiao Fangyu,Tang Wei,Fu Na.Wavelet Based De-noising Self-optimizing Method[J].Signal Processing,2012,28(4):577~586.
[8]赵瑞珍.小波理论及其在图像、信号处理中的算法研究[D].西安:西安电子科技大学,2001.Zhao Ruizhen.Study on Wavelet Theory and Its Algorithms for Image and Signal Processing[D].Xi'an:Xidian University,2001.
[9]程佩青.数字信号处理[M].北京:清华大学出版社,2001.
[10]刘明才.小波分析及其应用[M].北京:清华大学出版社,2005.
[11]盖 强,张海勇,徐晓刚.Hilbert-Huang变换的自适应频率多分辨分析研究[J].电子学报,2005,33(3):563~566.Ge Qiang,Zhang Haiyong,Xu Xiaogang.Study of Adaptive Frequency Multiresolution Analysis of the Hilbert-Huang Transform[J].Acta Electronica Sinica,2005,33(3):563 ~566.

