一种改进的深空高动态微弱信号频率捕获算法*
甘 浩,张晓林,马月红,徐 驰,李 赞
(1北京航空航天大学 北京 100191 2北京跟踪与通信技术研究所 北京 100094)
引言
深空通信与传统的近地空间通信相比,具有鲜明的特点,其通信距离极其遥远的特点,造成信号时延长且非常微弱;而深空探测器的速度通常较快,可以达到第二宇宙速度,同时还可能伴随着加速度、加加速度等,导致信号多普勒动态范围很大[1]。要实现深空探测过程中地面站与探测器的通信,则必须先解决高动态微弱信号频率捕获问题。
目前,针对高动态微弱信号的频率捕获方法有很多。文献[2]给出了一种基于线性预测器的频率估计算法,但该算法仿真并不是在极低信噪比条件下进行的,因此,其结论不适用于深空通信。文献[3]对基于极大似然法(ML)的频率估计算法、基于扩展卡尔曼滤波器(EKF)的频率估计算法和交叉的频率自动控制环路算法这三种算法的高动态微弱信号频率估计性能进行比较,得出的结论是基于极大似然法的频率估计算法更适用于高动态微弱信号的频率估计,但是由于该文未对极大似然法进行优化,因此计算复杂度高,难以在实际中应用。文献[4]提出了交叉模糊函数法结合Zoom FFT估计多普勒动态的方法,以较低的复杂度实现了信号多普勒动态的精确估计,但该方法仅适用于多普勒频偏较小的情况,且信噪比要达到-10dB以上。文献[5]提出了多支路时域变化率匹配FFT模值选大频率估计算法,能够在低信噪比条件下捕获多普勒频率及其一阶变化率,但是该方法要求的时域变化率匹配精度高,因此在高动态条件下需要的匹配支路数据巨大,导致计算量极其庞大,限制了该方法在实际中的使用。文献[6]提出了基于周期图谱的极大似然算法,相比文献[5]的方法降低了多普勒变化率的匹配精度要求,在相同动态条件下,减少了运算量,该方法已应用在美国探火活动中。文献[7]对文献[6]的方法做了改进,进一步减少了算法运算量,但捕获性能并没有提高。
本文研究了文献[6]的算法原理,分析得知其在求平均周期图谱时各个子数据段之间存在着多普勒频率变化率差值,导致非相干累加不能达到最佳性能。本文据此提出了一种频域循环移位累加求周期图的改进算法,有效地提高了算法的频率捕获性能。
1 基于极大似然法的频率估计
深空通信中接收端接收到的信号经过下变频后,频率成分中包括中频、多普勒频率、多普勒频率变化率及其更高阶变化率。在捕获阶段,不考虑多普勒频率二阶及以上的变化率[6],因此可以用恒变化率模型来分析接收信号。不失一般性,设中频为零,接收信号的复数形式为

式中,A=±1为调制信息,fd为多普勒频率,fd1为多普勒频率变化率,n(t)为零均值的加性高斯白噪声,其方差为σ2。下面讨论估计fd与fd1的方法。
深空通信中用于估计载波多普勒频率fd与多普勒频率变化率fd1的方法是基于极大似然法的频率估计法[6],该方法对信号频率的捕获过程实质上是对载波频率空间和载波频率变化率空间的搜索过程,即将输入信号与假设的Nr个频率变化率空间内不同的频率变化率相乘,得到
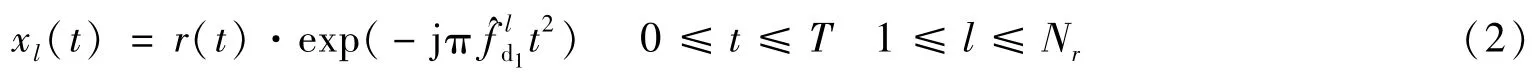
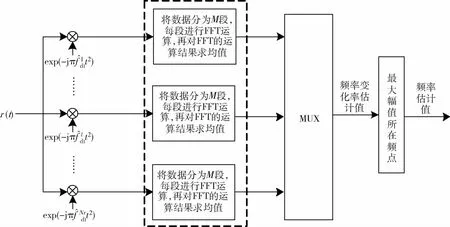
图1 基于极大似然法的频率估计原理Fig.1 Principle diagram of frequency estimation based on maximum-likelihood method
输入信号与各个支路预设的多普勒频率变化率相乘,当某一支路的多普勒频率变化率与实际的多普勒频率变化率最接近时,该支路求得的平均周期图会出现最大峰值,而最大值所在位置即为估计频率,该支路所预设的多普勒频率变化率即为估计的多普勒频率变化率。
2 算法缺陷
结合式(1)、式(2)可得
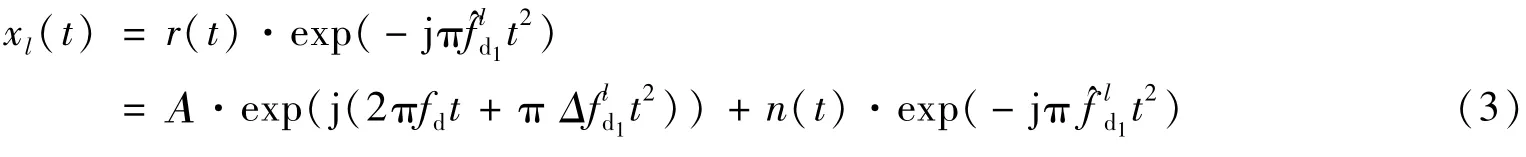

式中,h(t)是宽度为Ts的矩形窗,N代表噪声项。
3 算法的改进
针对第2节分析的算法缺陷,本文提出一种频域循环移位累加求周期图的改进算法。在图1虚框内求平均周期图环节,第一个子数据段的频谱保持不变,其余各段均根据及m(m=2,…,M)的值进行不同点数的循环移位操作,然后对循环移位后的各子数据段频谱绝对值的平方进行非相干累加。下面推导每个子数据段的频谱做循环移位的点数Sm。算法采用的采样频率为fs,每个子数据段做FFT变换的点数为NFFT,则FFT变换的分辨率为fs/NFFT,由式(4)得到支路l的第m(m=1,2,…,M)个子数据段的DFT绝对值表达式为
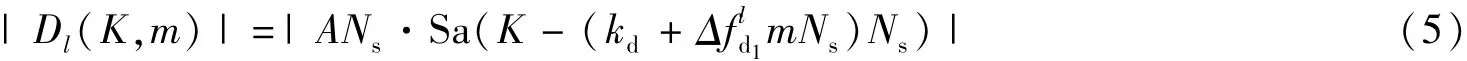
式中,Ns为时间Ts内的点数,kd为多普勒频率偏移量。做Sm点循环移位后,式(5)变为

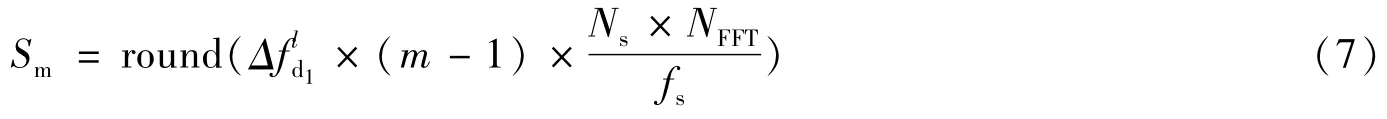
式中,round(·)表示四舍五入取整运算,m=2,…,M。循环移位的方向与的符号有关,当实际频率变化率小于预设的频率变化率时,向左移位;反之,向右移位。
采用改进算法求周期图时,在原算法的基础上,增加了移位点数的计算及相应的移位操作。由式(7)可知,在求每一个子数据段时增加了4次乘法运算和1次移位操作,因此改进算法在每次求周期图时多执行了4(M-1)次乘法运算和(M-1)次移位运算。由于算法中的M值不大,因此改进算法只略微地增加了算法的复杂度。
4 仿真验证
4.1 参数设置
在进行仿真时,系统的仿真参数,包括采样频率fs、FFT点数NFFT、非相干累加次数M等,需要根据信号特性及系统性能要求进行合理设置。设多普勒频率范围为[fdmin,fdmax],多普勒频率变化率的范围为[fd1min,fd1max],多普勒频率的分辨率为fd_res,多普勒频率变化率的分辨率为fd1_res,捕获概率要达到90%以上。在相同的系统参数条件下,仿真比较原算法和改进后算法的性能。下面分析几个主要仿真参数的选取原则。
①采样频率fs:在假设中频频率为零的前提下,采样频率要保证多普勒频率范围内的信号均能被采样,即满足奈奎斯特采样定理fs≥2(fdmax-fdmin)。本文取满足奈奎斯特采样定理的最小值,即两倍的多普勒频率范围。
②FFT点数NFFT:信号频率捕获阶段的频率精度要能够满足后级跟踪阶段对信号精度的要求,而跟踪阶段对多普勒频率精度的要求就是FFT分辨率要达到的精度,即fd_res=fs/NFFT,因此NFFT=fs/fd_res。
③信号持续时间T:在载波频率捕获阶段,忽略了多普勒频率变化率二阶及其以上阶数的参数,这样处理是基于在时间T内多普勒频率变化率二阶及其以上阶数参数值很小,以至于可以在时间T内把多普勒频率变化率看作常量。因此,T值要根据深空信号的动态特性选取。
④非相干累加次数M:为提高捕获概率,除了尽可能地增加功率谱峰值外,还要尽量减小噪声功率谱方差。因为功率谱方差正比于1/M,所以多次累加能有效减小噪声功率谱方差。但实际M不可能无限大,在采样率fs、时间T、FFT点数NFFT都确定的条件下,M=fs·T/NFFT。
4.2 仿真结果
以美国“挑战者”号火星探测器的进入(Entry)阶段为例[6],载噪比在17dB-Hz~20dB-Hz的范围内变化,多普勒频率fd变化范围-50kHz~50kHz,多普勒频率变化率fd1为0~800Hz/s。跟踪阶段要求载波多普勒频率捕获精度达到fd_res≤20Hz,对多普勒频率变化率的精度要求为fd1_res≤80Hz/s。根据4.1节对参数设置的分析,设采样频率fs=200kHz,FFT点数NFFT=10000,信号持续时间T=1s,非相干累加次数M=20。
图2为原算法与改进算法在不同载噪比条件下仿真得到的载波捕获概率Pa,每种载噪比条件下均进行1000次仿真,并对结果进行统计。由图2可以看出,在相同的捕获概率条件下,改进算法所需的载噪比较原算法低1dB-Hz~2dB-Hz。改进算法对信号载波频率的捕获性能有所提升。
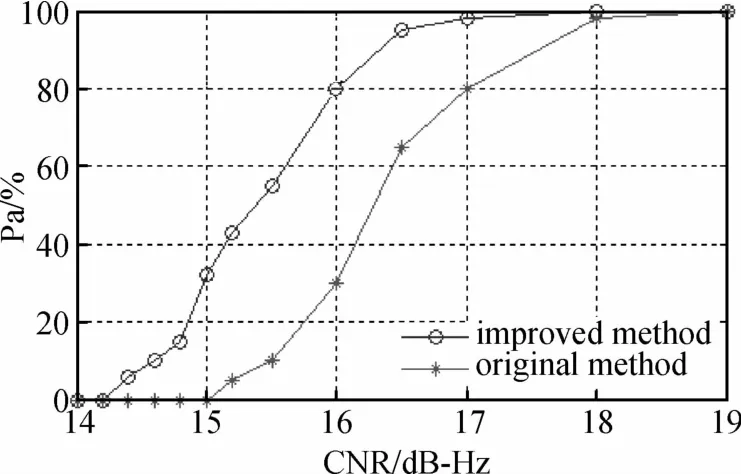
图2 原算法与改进算法在不同载噪比条件下的捕获概率Fig.2 Acquisition probabilities of original method and improved method with different CNR
输入信号中存在噪声,当噪声比较大时,捕获结果可能是虚警。图3为原算法与改进算法在不同载噪比条件下的虚警概率Pf。由图3可以看出,在相同载噪比条件下,改进算法的虚警概率有所降低。
由于改进算法对信号频谱进行了循环移位,消除了多普勒频率变化率差值的影响,因此捕获到的载波频率精度更高。图4是不同载噪比条件下捕获到的多普勒频率与实际多普勒频率的标准差,由该图可以看出仿真结果与理论分析相吻合。
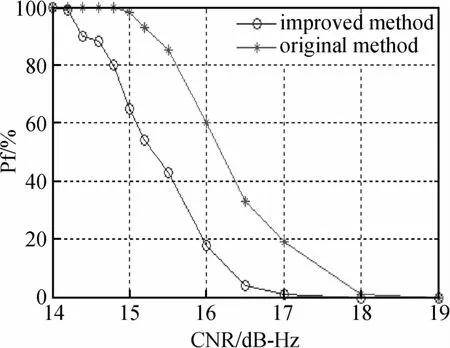
图3 原算法与改进算法在不同载噪比条件下的虚警概率Fig.3 False alarm probabilities of original method and improved method with different CNR
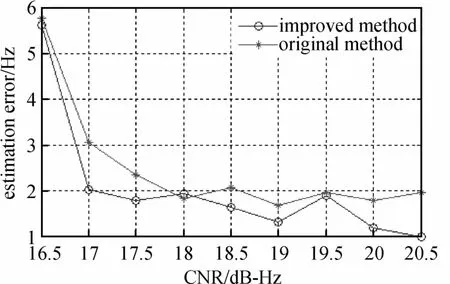
图4 不同载噪比条件下多普勒频率估计误差Fig.4 Estimation error of Doppler frequency with different CNR
5 结束语
本文研究基于极大似然法的深空高动态微弱信号频率捕获算法,发现其在求平均周期图时各个子数据段之间存在频差。针对该问题,本文提出了一种频域循环移位累加求周期图算法,推导了循环移位点数与频率分辨率等参数之间的关系,最后通过仿真验证了改进算法的正确性与有效性。
[1]刘嘉兴.走向深空——测控通信的发展方向[J].电讯技术,2006,(2):1~8.Liu Jia xing.Forward to the Deep Space Developing Trend of TTC&DT Technology[J].Telecommunication Engineering,2006,(2):1 ~8.
[2]Jackson L B,Tufts D W,Soong F K,and Rao R M.Frequency Estimation by Linear Prediction[C]//IEEE International Conference on ICASSP,1978:352 ~356.
[3]Vilnrotter V A,Hinedi S,Kumar R.Frequency Estimation Techniques for High Dynamic Trajectories[J].IEEE Transactions on Aerospace and Electronic Systems,1989,25(4):559 ~577.
[4]Ma SX,Jiang J N,Meng Q.A Fast,Accurate and Robust Method for Joint Estimation of Frequency and Frequency Rate[C]//IEEE International Symposium on Intelligent Signal Processing and Communication Systems(ISPACS2011),2011:1~6.
[5]韩孟飞,崔 嵬,王永庆,吴嗣亮.极低载噪比高动态信号的捕获策略研究与仿真[J].系统仿真学报,2009,21(23):7589~7592.Han Mengfei,Cui Wei,Wang Yongqing,Wu Siliang.Study and Simulation of Acquisition Technique for Extremely Low-CNR High-dynamic Signals[J].Journal of System Simulation,2009,21(23):7589 ~7592.
[6]Satorius E,Estabrook P,Wilson Jand Fort D.Direct-to-Earth Communication and Signal Processing for Mars Exploration Rover Entry,Descent,and Landing[R].IPN Progress Report,2003,42 ~153.
[7]段瑞枫,刘荣科,周 游,王润昕,侯 毅.一种低复杂度的极低信噪比高动态信号载波粗捕获算法[J].航空学报,2013,34(3):662 ~669.Duan Ruifeng,Liu Rongke,Zhou You,Wang Runxin,Hou Yi.A Low-complexity Coarse Carrier Acquisition Algorithm for Signals with Extremely Low Signal Noise Ratio and High Dynamics[J].Acta Aeronautica et Astronautica Sinica,2013,34(3):662 ~669.
[8]Cowell D M J,Freear S.Separation of Overlapping Linear Frequency Modulated(LFM)Signals Using the FractionalFourier Transform[J].IEEE Transactions on Ultrasonic,Ferroelectrics and Frequency Control,2010,57(10):2324 ~2333.

