An Analytical Model of Ballistic Impact on Light Ceramic/Metal Lightweight Armours
HOU Hai-liang,ZHONG Qiang,ZHU Xi
(College of Naval Architecture and power,Naval Univ.of Engineering,Wuhan 430033,China)
An Analytical Model of Ballistic Impact on Light Ceramic/Metal Lightweight Armours
HOU Hai-liang,ZHONG Qiang,ZHU Xi
(College of Naval Architecture and power,Naval Univ.of Engineering,Wuhan 430033,China)
To explore the design method of light ceramic composite armor,an approximate analytical model of ballistic impact on ceramic/metal composite armor focused on thin back plate and dishingshearing-petal failure is proposed,based on response characteristics experimental investigation and analysis of the response characteristics.The model takes the projectile’s erosion failure and ceramic fragments out of bullet surface into account,moving in the direction of lateral and the anti-impacting to get the dynamic impacting response and failure in the ceramic/metal composite armor metal back panel and formula of ballistic limit velocity of the ceramic/metal composite armor and calculation. Model analysis results are in good agreement with those obtained with the test results.
explosion mechanics;bullet proof model;high speed fragments; ceramic composite armor;deformation and energy absorption
0 Introduction
As ceramic materials are widely used in the design of protective armor for the protection of middle and high speed impact,the impact response characteristics of ceramic materials have been extensively and in-depthly studied[1].However,little energy will be absorbed in the penetration process due to the brittleness and low tensile strength of the ceramic.In the practical applications,ceramic as panels and back panel made of metal materials or fiber-reinforced composite materials are combined to form composite armor structures such as ceramic/metal, ceramic/composite materials combinations to improve its ballistic performance[2].As metal materials have high strength,better ductility and other features,they can provide a rigid support for ceramic panels to the benefit of mushrooming,eroding,fragmenting projectiles and reducing penetration performance,firstly;Then,they can make full deformation to absorb kinetic energy[3]of the projectile.
There are three different investigation approaches can be followed:the empirical method, numerical simulation and analytical modelling.The empirical method is the most widely used, but it costs too much,and its results are only valid for the specific projectile and target systems.The numerical simulations method requires not only high performance computers to calculate for a long time,but also a lot of material parameters difficult to be determined.So the theoretical method has become an important mean in the ballistic performance research of lightweight ceramic composite armor,by assuming some hypotheses which simplify the actual mechanisms of the penetration process[2].Now,a series of theoretical analytical models to describe lightweight ceramic/metal composite armor penetration process have been proposed.Such as ballistic limit estimation model of Florence[4-5],analytical models by Reijer[6]which consider the erosion and mushrooming of projectile and different backplate deformation modes,as well as analytical models of the constitutive behavior of ceramic powders after fragmentation of ceramic materials;analytical models proposed by Zaera et al[7]used in the ceramic/metal composite armor on the front and oblique shocks,and so on.The stress wave propagation was ignored in all of these models,and the impact process was divided into several time periods to respectively analyse the impulse response of ceramic panel and back metal panel.
Based on the experimental and analytical results of ballistic impact characteristic of ceramic/metal composite armor in Ref.[3],a theoretical analytical model of dynamic response under the action of impact load was proposed in this paper,and which is verified by experiment.
1 The model hypothesis
The initial state of ceramic/metal composite armor under the impact of high speed fragments is shown in Fig.1.According to its responses characteristic,ignoring stress wave propagation process,the impact process can be divided into two stages.The first stage is by the projectile in contact with the ceramic panels to the end of the ceramic cone formation.At this stage,projectiles are eroded,but can not penetrate into ceramic panels,ceramic panels turning into ceramic cones,while the metal back plate remaining intact.At the second stage,back panel begins to move.Because the speed of ceramic cone is less than the initial velocity of projectile,the projectile will gradually penetrate and promote ceramic cone,and make parts of ceramic fragments flow in the the lateral and reverse impacting direction.When the speed of projectile equals with that of ceramic cone,they will impact the back plane together,so the second stage can be divided into two sub-stages:sub-stage of projectile penetrating into ceramic cones and sub-stage of the remaining ceramic cones impacting backplate.To facilitate the analysis,according to the result of the Ref.[3],some basic assumptions are as follows:
(1)Projectile behavior
The main approach to destroying energy absorption of projectile is the erosion of projectiles,ignoring the mushrooming deformation of projectiles and bending deformation of its petals. Assume that the projectiles are ideal rigid plastic materials and the initial impacting velocity of the projectile is V0.
(2)Ceramic tile
Assume that the ceramic tile is an infinite plate and its thickness is hc.Since the energydissipated in the formation of new surface due to fragmentation of ceramic is only a small fraction of the kinetic energy of the projectile(about 0.2%of total),a large part of impacting kinetic energy of the projectile redistributed as the kinetic energy of ceramic pieces[8].Therefore,ignoring the forming process of ceramic cone,we assume that the projectile and the ceramic cone effect on the backplate as a whole together.Assume that the diameter of the top ceramic cone equals to that of projectile[3]and its half cone angle is 65°.
(3)Back plate
Assume that back plate is a infinite rigid plastic thin plate,whose thickness is hb,and dynamic yield strength is Yb.We assume the deformation failure mode of the metal backpanel:dishing-shearing-petal failure and dishing-petal failure
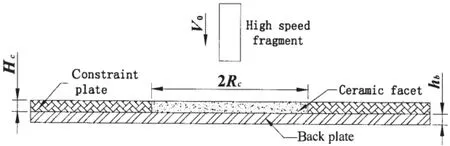
Fig.1 Schematic of initial condition
2 The shock response of the projectile and the ceramic tile
2.1 StageⅠ
In the initial stage of the projectile impact on the ceramic panel,the projectile is eroded, but cannot penetrate into the ceramic panel,because the penetration resistance of ceramic materials is much greater than the compressive strength of the projectile.The compression wave in ceramic tile caused by the projectile impact,propagates to the back of the panel,and then causes tensile wave when it reflected on the back panel,and all of these cause the ceramic panel conical crashing failure.Although,the fragmentation of the ceramic materials is throughout the whole process of penetration,but according to the analysis of Den Reijer[6]and Wilkins[9], fragmentation occurs mainly in the initial stage of the impacting process.Den Reijer assumed that when the compression stress wave propagates throughout the thickness of the ceramic panel,the back of the panel began to crack,and when the cracks generated on the back of the panel propagate to the target surface,ceramic cone forms.Therefore,the time required for forming the ceramic cones is:

where hcis the thickness of ceramic tile,ulongis the velocity of the longitudinal stress wave, vcrackis the radial crack propagation speed.To coincide with the value of the time of duration in the first stage referred by Wilkins[9],Den Reijer assumed that the value of vcrackequals to 1/5 of ulong.Therefore:half angle of ceramic cone is about 65°[9]。
We take the Tate-Alekseevskii[10-11]equation to describe projectile’s erosion:

among them,Ypis the dynamic yield strength of the projectile’s material,ρpis the density of the projectile,V(t)is the velocity of the projectile,V(0)=0;L(t)is the length of the projectile.For non-cylindrical projectiles,the equivalent diameter and length are selected according to the following equation:

where Lpis the actual length of the projectile,Mpis the mass of the projectile,D(z)is the diameter of the position z.
2.2 StageⅡ
Assuming the projectile impacts the back plate at the same speed of Vr0with the ceramic cones.According to the conservation of momentum theorem:

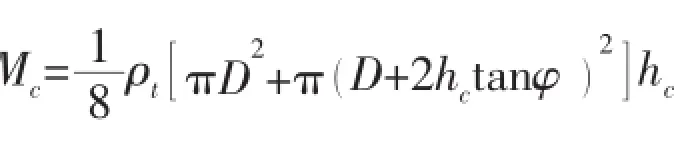
When the ceramic cones generatedt=tc(),the projectile begins to penetrate and promote ceramic cones,and ceramic materials in front of the projectile gradually separate from the surface of the warhead,moving to the side and anti-impacting direction.Ceramic material between the projectile and the back plate becomes thinner gradually.The speed of projectile’s tail is V(t),but the speed of the projectile-ceramic interaction surface is Vi(t).The difference between the two velocities is the erosion velocity of the projectile for this stage.The thickness of ceramic cones is hcone(t),whose speed is Vcone(t).The difference between Vcone(t)and Vi(t) is the speed of the projectile penetrating into ceramic cones.
When the ceramic cones generatedt=tc(),the back plate begins to move.As the deformation of the back plate at the beginning stage is very small,the displacement and the movements of other parts can be neglected.That is,we can assume that only the part m of the back plate which contacts with the bottom surface of ceramic cones begins to move,and its moving speed equals to that of the ceramic cones,but no displacements are generated.
(1)When V(t)>Vi(t)
Tate-Alekseevskii[10-11]equation can be used to describe projectile’s erosion:
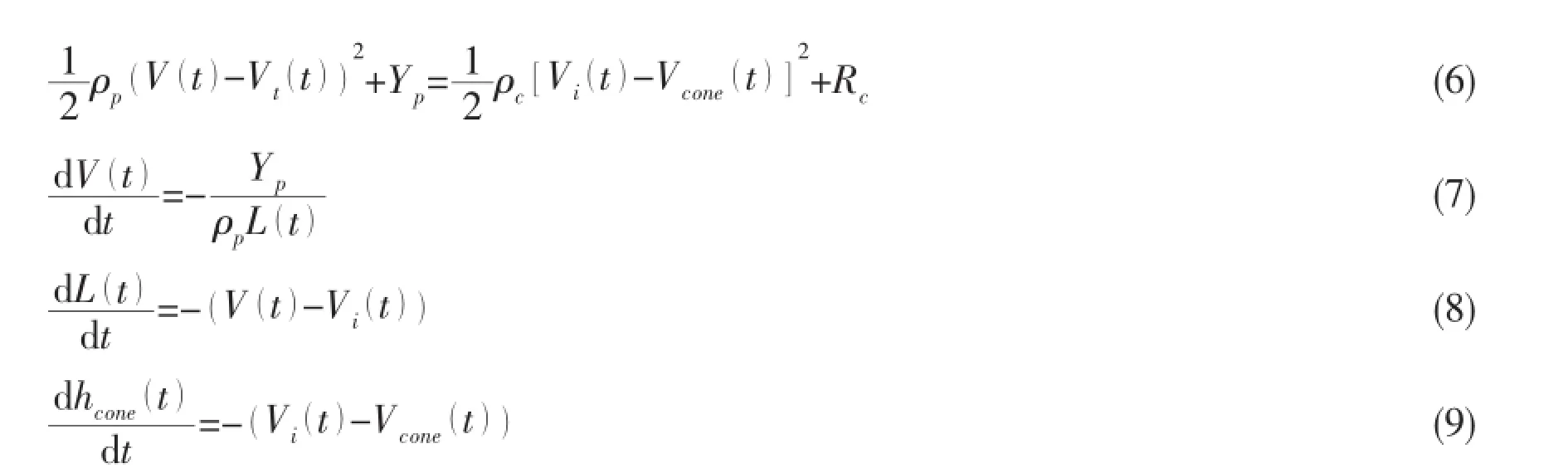
where Rcis the penetration resistance of the ceramic panel.According to Ref.[12],when there is cover plate constraint,the penetration resistance Rcdecreases with the change of the thickness of the ceramic tile for Al2O3ceramics with the density of 3.6 g/cm3.When the thickness of the ceramic tile is more than 24 mm,Rckeeps steady at about 8 000 MPa;For Al2O3ceramics without cover plate constrants,Rcis about 5 100 MPa when the thickness of the ceramic tile is from 27.81 mm to 41.96 mm;For the ceramic cone fragmentations,Rcis less than the value above.ρpand ρcare the densities of the projectiles and the ceramic materials,respectively.According to continuity conditions,the initial velocity and length of the projectile in the second stage equal to those of the ending of the first stage.When t≤tconoid=6hc/ulong,Vcone()t= Vi()
t=0.
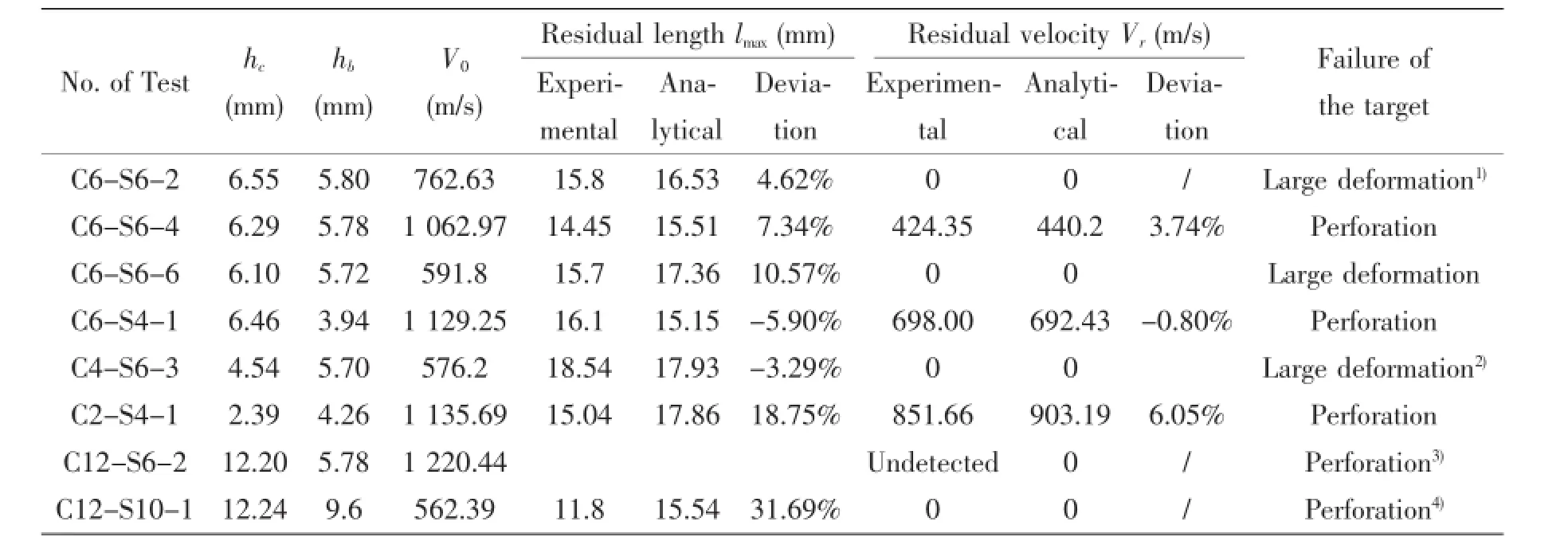
(2)When V(t)=Vi(t)
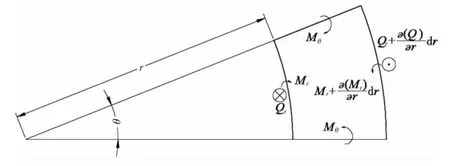
In solving Eqs.(6)~(9),it is possible to get results V(t) (a)When V(t)=Vi(t)>Vcone(t),the projectile continues to penetrate into the fragments of ceramic cones.At this time,the resistance of slowing down the projectile is offered by the ceramic cones.According to Newton’s Second Law,we can get: And the change of the thickness of the ceramic cones still meets the Eq.(9). (b)When V(t)=Vi(t)=Vcone(t)=Vr0,residual projectile and remaining ceramics impact the back plate with the same speed Vr0.The mass of the residual projectile Mprand the mass of the ceramic cone Mcrare respectively: where hcris the thickness of the residual ceramic cones a=RpLA()+hcrtan65°. Due to the axial symmetry of the problem,the cylindrical coordinate systemr,θ,()zis set up as shown in Fig.2.The origin of coordinate is located in the center of the undeformed plate and the axis of z directs vertically downward.The thickness of the back plate is 2H,andthe back plate is relaxed at the beginnin g.To simplify the expression,time is set to zero when the speed of the projectile equals to that of the ceramic cones in dynamic response analysis of the back plate.Assume that the area density of the metal back plate is μ1,and take μ2=(Mpr+Mcr)/(πa2)+μ1. 3.1 Yield criterion Suppose that the back panel is an ideal rigid-plastic material.So the three-dimensional von Mises yield criterion for the circular plate subjected to axisymmetric load is: where r,θ,z are coordinates of the cylindrical coordinate,and the origin of the coordinate is located in the center of the undeformed plate.Axis z directs vertically downwards.σrand σθare radial and circumferential stresses,respectively,τ is the shear stress of the r-z plane,and σ0is the yield stress of the material of the back plate. When the back plate occurs dishing-shearing-petal failure,shear force and bending moment are mainly dominated of the generalized stress in the back plate.Yield criterion can be written as: The von Mises yield criterion in three-dimensional coordinate system,whose axises are Mr,Mθand Q,respectively,is an ellipsoid.In this paper, piecewise liners(see Fig.3)approximate was used to describe the ellipsoid yield criterion,which is approximate description as: Fig.3 Yield criterion 3.2 Deformation assumption There will generate a plastic hinge circle on the fringes of the impact load whose radius is a.The second plastic hinge circle appears in the location where the shear force is zero,and its position changes over time(see Fig.4).Set r as the distance of any point on the surface to the center of the plate.The three regions of different deformation mechanisms of plate are the central part with a radius of a at the speed of vt,the outer area of R(t)≤r≤∞is free zone,and plastic deformation area of a≤r≤R(t)corresponds to B0C0C1B1.r is the radius of the perimeter of the plastic hinge circle,where R(t)is a function of time. Fig.4 Deformation hypothesis 3.3 Velocity field The energy dissipation rates calculated by stress and strain rate and by the general stress and general strain rate are the same,so: Assuming that shear strain rate is distributed uniformly along the thickness direction of the plate: From the Taylor expansion of radial velocity vr,we can get the radial velocity and the radial and circumferential strain rate as follows,by taking the first term: From Eqs.(17)~(19),we can get the expression of general strain rate as follows: According to the yield criterion and Eq.(20),the general strain rate of plastic zone a≤r≤R(t)can be expressed as: Normal velocity of the plastic zone is obtained by integrating the above equation for r: where K1and K2are the functions of time only.The material keep still on the outside plastic hinge circle of r=R(t).From Eq.(23),we can get: Assuming that the velocity of the plastic zone on the back plate of the plastic hinge is v. From Eq.(23)we can get: Substituting Eq.(24)into Eq.(25),we find: To simplify the equation,we make: From Eq.(23),we can get the velocity field of the plastic zone a≤r≤R()t,which can be expressed as: 3.4 Balance equation and its solution Ignoring the rotation inertia effect,balance equations of elements in Fig.5 are: Fig.5 Schematic of the force on micro elements of the back plate where μ is the mass of the back plate per unit area.From Eq.(29),the dynamic equilibrium equation can be expressed as: According to the yield condition,the circumferential moment Mθcan be eliminated before integration.Substitute the acceleration field Eq.(28)into equilibrium Eq.(30),the equilibrium equation of the central part 0≤r≤a on the back panel can be expressed as: Substitute Eq.(28)into Eq.(32),we can get: The expression of Q is the Eq.(33)divided by r on the right side,therefore: Because that when r=R(t),Q=0,from Eq.(33),we can get: To solve the simultaneous differential equations(34)and(35),we get the dynamic response of the back plate. 3.5 The deformation and failure of the back plate On the other hand,the velocity of the projectile,ceramic cones and the central part 0≤r≤a of the back plate are: (1)Bulging and dishing deformation failure When the slip velocity equals to 0,Z1=v=U,Shear slip stops,the back is not penetrated and bulging and dishing deformation failure occurs in the back panel. Eqs.(34)and(35)turn to: Iterative solution to calculate Z1and Z2need continuing by Eqs.(38)and(39)until Z1equals to 0 and the response of the back plate ends. (2)Dishing-shearing-petal failure When the shear slip distance is greater than the thickness of plate,the back plate is penetrated,and shear failure will occur.At this time,U is the residual velocity of the projectile, and Eqs.(34)and(35)turn into: Iterative solution to calculate Z1and Z2is continued by Eqs.(40)and(41)until Z1equals to 0 and the response of the back panel ends. In order to verify the accuracy of ballistic analysis model,results of the analysis are compared with Ref.[3],and calculation parameters are shown in Tab.1. Tab.1 Parameters for calculation Tab.2 shows the comparison of experimental and analytical results on residual length and velocity.The table illustrates that most of remaining length of the projectile is larger than that the experimental results,because the erosion and the mushrooming deformation were ignored. But due to the fact that target plate is penetrated or the initial impacting velocity of the projectile is close to the ballistic limiting velocity of the target,the deviation of the most of the results is less than 20%.According to the experimental results,the energy absorbed due to the damage of the projectile is about 5%~12%of its initial impact kinetic energy.Therefore,because of this approximation,during the penetrating process,the total deviation of calculation results of the energy absorption is within 2.4%.The deviation between experimental and analytical results of residual velocity is less than 10%. Tab.2 Relationship between experimental and analytical results on residual characteristic An approximate analytical model focused on thin back plate and dishing-shearing-petal failure of ceramic/metal composite armor subjected to ballistic impact was proposed,according to the results of the experimental investigation.The erosion failure of the projectile and the movement in the direction of lateral and the anti-impacting of ceramic fragments were taken into account in the analytical model.The dynamic response and failure mode of metallic back plate of the ceramic/metal composite armor were obtained.The formulas of ballistic limit velocity of the ceramic/metal composite armor and calculation methods of residual velocity of projectile were proposed.Model analysis results are in good agreement with those obtained with the test results. [1]Hou Hailiang,Zhu Xi,Kan Yulong.Advance of dynamic behavior of ceramic material under the impact of projectile[J]. Acta Armamentarii,2008,29(1):94-99.(in Chinese) [2]Hou Hailiang,Zhu Xi,Kan Yulong.Advance of ballistic performance of light ceramic composite armour under the impact of projectile[J].Acta Armamentarii,2008,29(2):208-216.(in Chinese) [3]Hou Hailiang,Zhu Xi,Li Wei.Investigation on bullet proof mechanism of light ceramic/steel armor[J].Acta Armamentarii, 2013,34(1):105-114.(in Chinese) [4]Florence A L.Interaction of projectiles and composite armor plate[R].Stanford Research Institute,Menlo Park,CA,USA., AMIVIRG-CR-69-15,August,1969. [5]Hetherington J G,Rajagopalan B P.An investigation into the energy absorbed during ballistic perforation of composite armors[J].Int.J Impact Engng.,1991,11:33-40. [6]Den Reijer P C.Impact on ceramic faced armour[D].Ph.D.Thesis,Delft Technical University,The Netherlands,1991. [7]Zaera R,Sánchez-Gálvez V.Analytical modelling of normal and oblique ballistic impact on ceramic/metal lightweight armours[J].Int.J Impact Engng.,1998,21(3):133-148. [8]Woodward R L,Gooch W A,Jr R G O’Donnell,et al.A study of fragmentation in the ballistic impact of ceramics[J].Int. J Impact Engng.,1994,15(5):605-618. [9]Wilkins M L.Mechanics of penetration and perforation[J].Int J Eng Sci,1978,16:793-807. [10]Tate A.A theory for the deceleration of long rods after impact[J].J Mech.Phys.Solids,1967,15:387-399. [11]Tate A.Further results in the theory of long rod penetration[J].J Mech.Phys.Solids,1969,17:141-150. [12]LI Ping.Dynamic response of ceramic and mechanism against long rod penetrators[D].Beijing:Beijing Institute of Technology,2002.(in Chinese) [13]Anderson C E,Jr Morris B L.The ballistic performance of confined Al2O3 ceramic tiles[J].Int.J Impact Engng,1992,12 (2):167-187. 轻型陶瓷/金属复合装甲抗弹分析模型研究 侯海量,仲强,朱锡 为探讨轻型陶瓷复合装甲结构设计,在弹道冲击响应特性试验研究与分析的基础上,针对薄金属背板支撑的陶瓷复合装甲,以金属背板发生碟型变形—剪切—花瓣型失效为分析对象,建立了陶瓷/金属复合装甲侵彻过程的近似解析模型。模型考虑了弹体的侵蚀失效及陶瓷碎片脱离弹头表面,向侧向和反冲击方向的运动,得到了陶瓷/金属复合装甲中金属背板的动态冲击响应及失效,陶瓷/金属复合装甲的弹道极限速度计算公式和弹体的剩余速度计算方法,模型分析结果与试验结果吻合良好。 爆炸力学;抗弹机理;高速破片;陶瓷复合装甲;变形吸能 O344.7 :A 侯海量(1977-),男,海军工程大学高级工程师,硕士生导师; 1007-7294(2015)12-1535-14 O344.7 :A 10.3969/j.issn.1007-7294.2015.12.010 仲强(1990-),男,海军工程大学硕士研究生; 朱锡(1961-),男,海军工程大学教授,博士生导师。 Received date:2015-07-04 Foundation item:Supported by the National Natural Scinence Foundation of China(Grant Nos.51179200 and 51209211) Biography:HOU Hai-liang(1977-),male,senior engineer of Naval Univ.of Engineering,E-mail:hou9611104@163.com; ZHONG Qiang(1990-),male,master;ZHU Xi(1961-),male,professor/tutor.
3 The impact response of the metal back plate


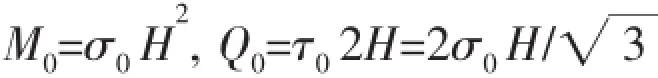






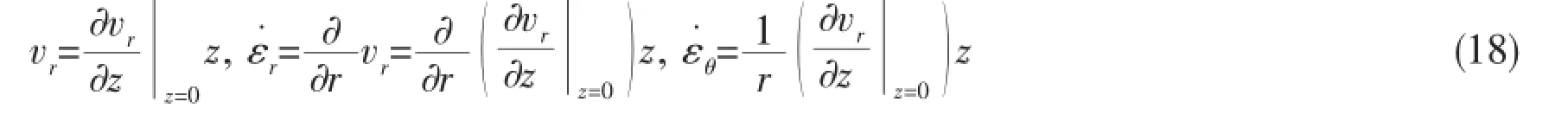



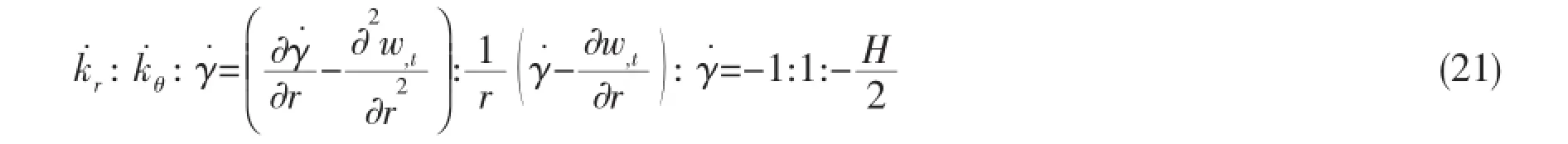
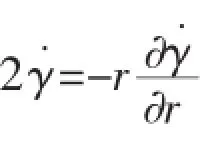





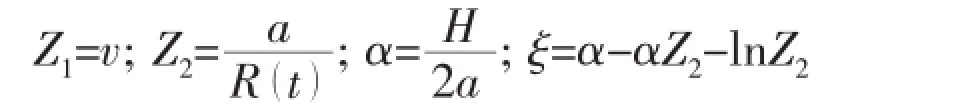

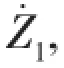




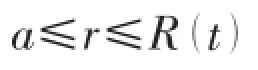

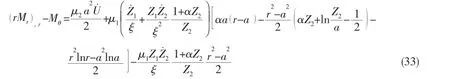

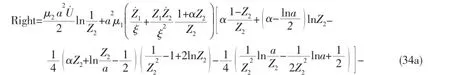
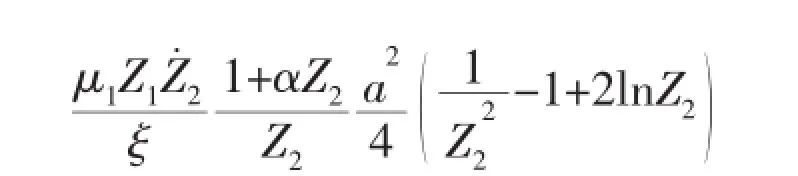
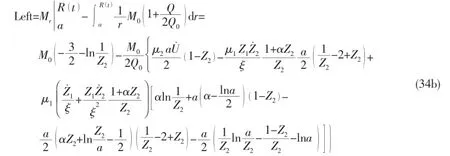
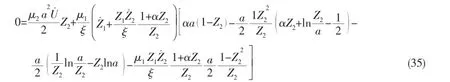




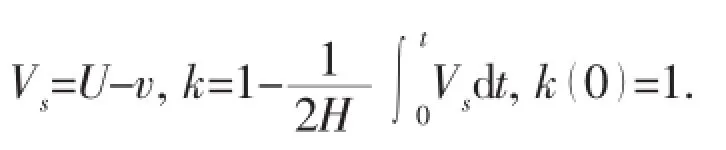

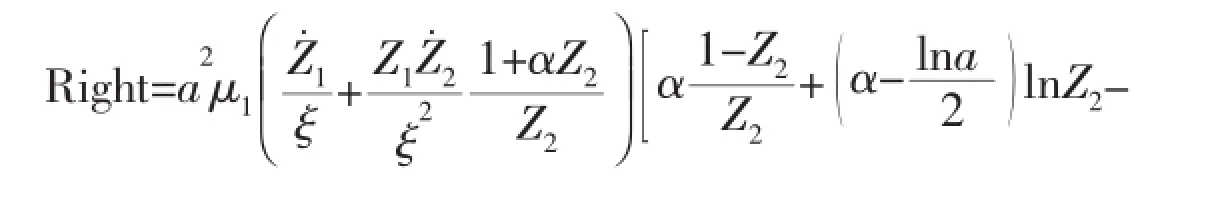
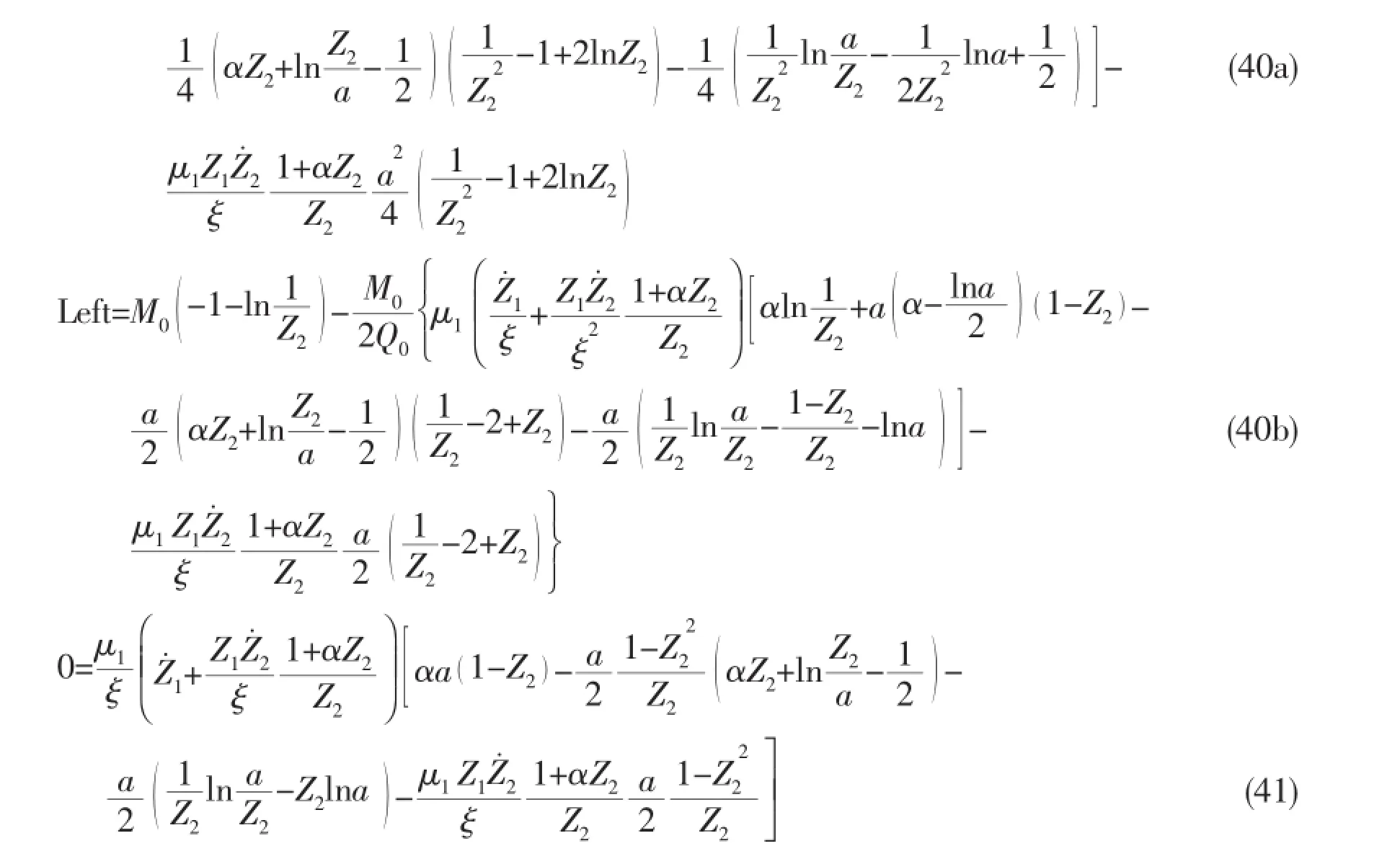
4 Experimental verification

5 Conclusions
(海军工程大学舰船工程系,武汉430033)
- 船舶力学的其它文章
- Active Control of Low-Frequency Sinusoidal Vibration Transmission of Ship Machinery
- Analysis on Factors Influencing Strains of Unbonded Flexible Risers Under Pressures
- Tensile Fatigue Test Method for Typical Stiffened Panel
- Theoretical and Numerical Research on CTOD for Ship Plate under Cyclic Loading Considering Accumulative Plastic Strain
- A New Concept of ETLP and Its Hydrodynamic Performance
- Study on the Dynamic Response and Tension Characteristics of a TLP with One Tendon Broken

