基于对偶理论的本体稀疏向量学习算法*

高 炜

(云南师范大学 信息学院,云南 昆明 650500)



基于对偶理论的本体稀疏向量学习算法*

高 炜

(云南师范大学 信息学院,云南 昆明 650500)

作为一种语义计算和结构化信息存储模型，本体已被广泛应用于生物、物理、地理信息系统等多个领域.在本体学习算法中，本体图顶点所对应的概念信息用一个多维向量来表示.但在大部分应用背景下，顶点之间的相似度取决于少部分分量.基于对偶理论得到本体稀疏向量的计算方法，将该算法应用于数学本体和大学本体，通过P@N准备率来说明算法的效率.

本体; 相似度计算; 本体映射; 稀疏向量

1 引 言

传统的启发式本体计算方法已经无法胜任大数据量的本体相似度计算，因而利用各种学习算法来得到本体相似度计算函数和本体映射已成为近几年研究的重点.本体数据模型可用图G=(V,E)来表示，一类本体学习算法其基本思想是得到一个实值本体函数f：V→.该本体函数的作用是将所有本体顶点映射到实数轴，从而顶点对应的概念之间的相似度可以用它们对应的实数在数轴上的距离来衡量.

文献[1]提出了正则化框架下的半监督本体算法，在计算模型中充分利用未标记数据的相关信息，同时将数据嵌入到特征空间，利用特征表示得到相关算法；文献[2]从线性欧氏空间及再生核希尔伯特空间出发，得到有噪条件下的新正则化求解模型，同时将注意力集中到假设空间的设置上；文献[3]给出基于优先图本体相似度计算方法；文献[4]得到基于迭代拉普拉斯的半监督本体学习算法；更多本体学习算法可参考文献[5-7].有关本体算法的理论结果，可参考文献[8-9].

本文利用对偶技术得到递归计算方法来计算本体稀疏向量，通过本体稀疏向量再得到本体函数，最后由本体函数来计算概念顶点对应实数在数轴上的距离，从而确定概念之间的相似度.

2 算法描述

当使用机器学习方法进行本体相似度计算时，需要将每个顶点的信息用一个p维向量来表示.记v={v1,…,vp}是顶点v对应的向量.为了表示方便，用v来同时表示顶点以及对应的向量.本体学习算法最终目标是获得本体实值函数f:V→,通过顶点对应的实数在数轴上的距离来衡量顶点对应的概念之间的相似度.本体函数的本质是一种降维算子f:p→.

本体概念对应顶点的向量即包含了这个概念的所有语义信息，又涵盖了概念在整个本体图中的邻域关联信息.在实际应用中，向量的维度p会非常的大.例如在基因学本体中，所有基因信息可能都包含在一个向量中.此外，本体图复杂的图结构也增加了计算的复杂度，例如GIS本体.但在实际应用过程中，真正对概念之间相似度起决定作用的恰恰是p维向量中的少部分分量.例如在遗传本体应用中，导致某种遗传病发生的往往是少数基因，大部分基因与该遗传病无任何关系；在交通本体的实际应用中，假设某个地点产生交通事故并造成驾驶员或者路人受伤，那么需要寻找的是和事故发生地点最近的医院，其周边的办公楼和住宅与此无关，即我们的需求是寻找本体图中满足特定邻域结构特征的顶点(概念).由此，稀疏学习算法恰好适合这种本体应用.

具体地说，通过本体稀疏向量的学习，本体函数可作如下表示：

(1)

这里β=(β1,…,βp)是稀疏向量，其特点是大部分分量的值等于0；δ是与噪声有关的误差项.在忽略δ的前提下，由(1)可知，只要得到稀疏向量就可以确定本体函数f.因此，本体函数学习就归结为本体稀疏向量的学习.

设V∈n×p为本体信息矩阵，它的每一列对应一个顶点的向量，n为样本容量.本体稀疏向量β的学习模型可以写成如下矩阵形式：

(2)

l(Vβ)+λΩ(β)+l*(-κ)

本文将文献[12]中用于图像处理的FISTA方法加以改进，并用于本体模型(2)的求解：

输入：初始本体稀疏向量β(0)∈p，Ω表达式，平衡系数λ>0，对偶间隙的精确度ε>0.

参数设置：w>1，L0>0.

输出：本体稀疏向量β

初始值设置：y(1)=β(0)，t1=1，k=1.

Whileβ(k-1)对偶间隙>εdo

l(prox[λΩ](y(k))≤l(y(k))+(Δ(k))T

End while

返回β←β(k-1).

3 实 验

3.1 本体相似度计算实验

第一个实验是采用数学本体O1(其结构可参考图1)来验证本体稀疏向量学习算法对本体相似度计算的效率.采用P@N准确率[13]来评判实验结果的好坏.即对于本体图中任意顶点v∈V(G).设N∈表示实验中取与顶点v最相似的N个顶点.记

…

从而得到返回集

return(v)={v1,v2,…,vN}

再将return(v)与专家给出的与顶点v最相似的N个顶点进行匹配，计算准确率.最后计算所有顶点的平均准确率.

图1 数学本体O1

实验结果显示，P@1的平均准确率为30.77%，P@3的平均准确率为51.28%，P@5的平均准确率为69.23%.从而可知本算法对数学本体的相似度计算是有效的.

3.2 本体映射实验

第二个实验是验证本文稀疏向量学习算法对构建本体映射的效率.实验的目的是在两个“大学”本体O2和O3之间建立本体映射.实验结果同样采用P@N准确率来衡量.需要注意的是，本体映射中相似顶点的选取是在不同本体之间进行.

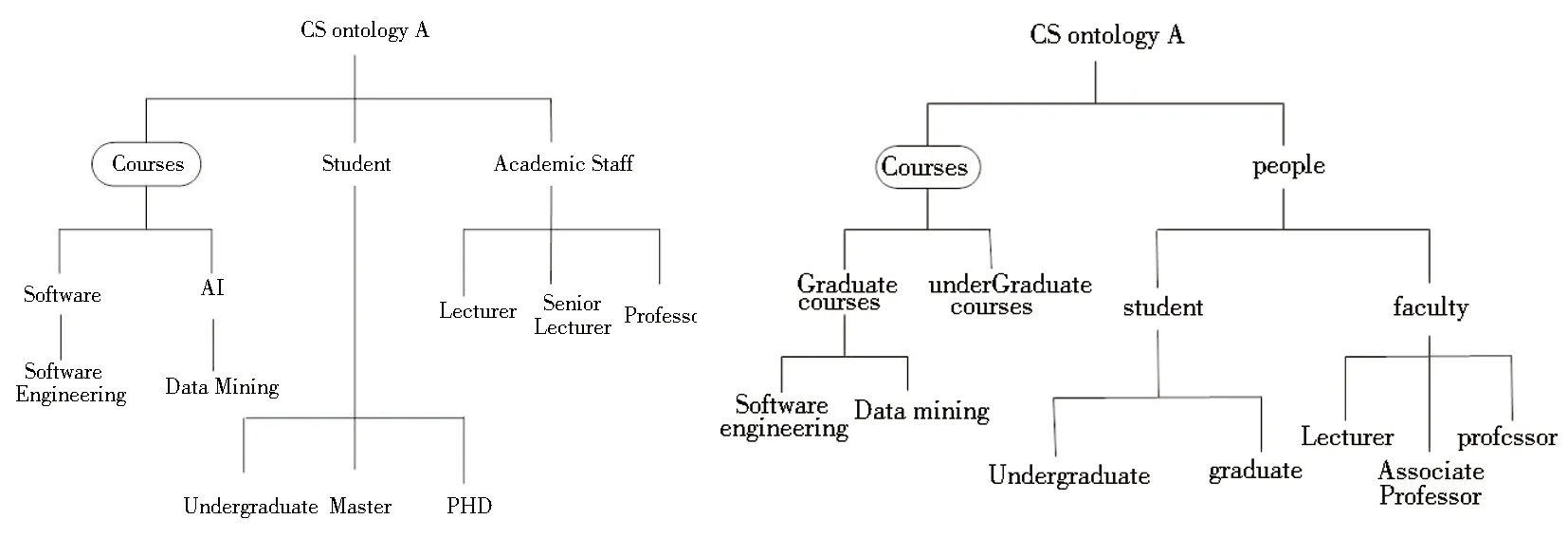
图2 “大学”本体O2 图3 “大学”本体O3

实验结果显示，P@1的平均准确率为46.43%，P@3的平均准确率为63.10%，P@5的平均准确率为85.71%.因此可知本文算法对两大学本体之间构建本体映射是有效的.

4 结束语

利用对偶理论，对文献[12]中用于图像处理的FISTA方法加以改进，从而得到本体计算模型(2)的循环计算策略.同时，通过实验数据验证了本体稀疏向量学习算法对数学本体相似度计算和大学本体之间构建本体映射是有效的.

[1] 朱林立，戴国洪，高炜.正则化框架下半监督本体算法[J].微电子学与计算机,2014,31(3):126-129.

[2] 朱林立，吴访升，叶飞跃，等.有噪条件下基于正则化模型的本体学习算法[J].西北师范大学学报:自然科学版,2014,50(6):41-45.

[3] 兰美辉，徐坚，高炜.基于优先图的本体相似度计算[J].科学技术与工程，2014,14(28):252-255.

[4] 彭波，徐天伟，李臻，等.迭代拉普拉斯半监督学习本体算法[J].计算机工程与科学，2014,36(11):2164-2168.

[5] 高炜,梁立,徐天伟,等.半监督k-部排序算法及在本体中的应用[J].中北大学学报：自然科学版，2013,34(2):140-146.

[6] 高炜，梁立，徐天伟.基于正则化瑞利系数的半监督k-部排序学习算法及应用[J].西南师范大学学报：自然科学版，2014,39(4):124-128.

[7] 高炜，高云，梁立.基于ε-邻域方法的本体映射算法[J].云南师范大学学报：自然科学版，2011,31(3):37-40.

[8] 高炜,张云港,梁立.Cs相似度函数下正则谱聚类的收敛阶[J].兰州大学学报：自然科学版，2011,47(2):109-111.

[9] 高炜,周定轩.与一般相似度函数相关的谱聚类的收敛性[J].中国科学:数学，2012,42(10):985-994.

[10]BORWEINJM,LEWISAS.Convexanalysisandnonlinearoptimization:theoryandexamples[M].Publisher:Springer,2006,50-60.

[11]JENATTONR,MAIRALJ,OBOZINSKIG,etal.Proximalmethodsforsparsehierarchicaldictionarylearning[C].InProceedingsoftheInternationalConferenceonMachineLearning,Haifa,Israel,487-494.

[12]BECKA,TEBOULLEM.Afastiterativeshrinkage-thresholdingalgorithmforlinearinverseproblems[J].SIAMJournalonImagingSciences,2009,2(1):183-202.

[13]CRASWELLN,HAWKINGD.OverviewoftheTREC2003webtrack[C].ProceedingsoftheTwelfthTextRetrievalConference，Gaithersburg,Maryland,NISTSpecialPublication,2003:78-92.

Duality Theory Based Ontology Sparse Vector Learning Algorithm

GAO Wei

(School of Information,Yunnan Normal University,Kunming 650500,China)

As a semantic computing and structured information storage model,ontology has been widely used in many fields of biological,physical,geographical information systems.In ontology learning algorithm,ontology graph vertices correspond to the information concept expressed as a multi-dimensional vector.However,in most application backgrounds,the similarity between vertices depends on small part of the component.In this paper,ontology sparse vector learning algorithm is obtained in terms of duality arguments.The algorithm is applied to the mathematics ontology and the university ontology, the efficiency of the algorithm is illustrated byP@Nratio.

Ontology; Similarity measure; Ontology mapping; Sparse vector

2015-01-25

国家自然科学青年基金资助项目(11401519).

高 炜(1981-)，男，浙江绍兴人，博士，讲师，主要从事机器学习和图论方面研究.

高 炜.

TP

A

1007-9793(2015)04-0046-05