钻井液流变参数计算新方法及流变模式优选

李 琪，王 涛，滕 藤，李二洋，白 磊

(1.西安石油大学 石油工程学院，陕西 西安 710065； 2.长庆油田 采油一厂，陕西 延安 716029)

钻井液流变参数计算新方法及流变模式优选

李 琪1，王 涛1，滕 藤1，李二洋1，白 磊2

(1.西安石油大学 石油工程学院，陕西 西安 710065； 2.长庆油田 采油一厂，陕西 延安 716029)

钻井液流变参数的准确计算和流变模式的优选是钻井液优化设计及钻井水力学计算的前提。针对常用的4种流变模式，分析了流变参数的常规算法及回归分析算法；利用0.618法非线性回归分析计算出了幂律模式和赫巴模式的流变参数，分析比较了钻井液流变模式的4种优选方法，得出拟合残差平方和方法为最有效的优选方法；开发了钻井液流变模式优选软件，可输出各流变模式的流变参数及最优流变模式，并结合实测数据进行了实例分析。

钻井液；流变模式；流变参数；回归分析；软件开发

钻井液是钻井工程的血液，在钻井过程中，钻井液的流变性可影响钻速、泵压、排量、钻井液的当量密度、岩屑的携带与悬浮以及固井质量等，直接关系到钻井安全和成本[1]。因此，控制钻井液的流变性非常重要。国内外学者先后提出了多种流变模式来描述钻井液的流变性，如幂律模式、宾汉模式、卡森模式及赫巴模式等。不同流变模式的提出也带来了一个问题：对于某一给定的钻井液体系和配方，如何选择一种最适合的流变模式来描述其实际流变性。虽然在常规井眼，钻井液的近似模拟对水力计算不会造成太大误差，但对一些特殊井眼，如小井眼，随着环空间隙的减小，环空压降对流变模式的选择变得相当敏感[2]。另外，随着工程技术理论实践和计算机技术的发展，高效、科学、安全的钻探必须依托精确的流变参数。因此，钻井液流变模式的优选及流变参数的计算就显得极为重要，其对评价钻井液性能、优选钻井水力参数及安全钻井等均具有重要意义。

1 常用钻井液流变模式及其参数常规算法

在钻井工程领域，常用钻井液流变模式的方程及流变参数的常规算法如表1所示[3]。常规计算方法简单易用，方便现场操作，因而得到了广泛的应用。但也有如下不足之处：(1)计算过程中只用了黏度计的1个或几个读数，未能充分利用实验数据；(2)常规算法得到的宾汉与幂律模式的流变参数只能反映流体中、高剪切速率下的流动规律，不能反映低剪切速率流动的环空流体的流动规律，会导致水力计算误差的增大；(3)文献和现场大量实验数据表明，φ3和φ6的数据因旋转黏度计内外筒环的液体呈塞流流动，读数不准确，这一点对于高密度钻井液尤为突出[4]，这也加剧了常规算法的不准确性。

随着计算机的广泛应用，结合数理统计的处理方法，完全可以充分利用旋转黏度计的6个读数，提高流变参数的计算精度，从而减小误差。

2 回归分析计算流变参数

在数理统计学上，把研究1个(或几个)自变量与1个随机变量之间的相关关系式所建立的数学模型及所作的统计分析称为回归分析[5]。目前计算流变参数的回归分析方法可分为线性和非线性回归分析2种，并且都是基于最小二乘原理。

2.1 线性回归分析

采用在流变方程等式两端取对数转换的方法，可将非线性流变模式转换为线性模式，统一用一元线性回归分析方法计算流变参数。各流变模式的线

性回归模型[6-7]如表1所示。

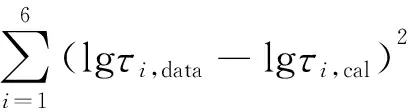
表1 各流变模式流变参数常规算法及线性回归模型

注：φ3、φ6、φ100、φ200、φ300、φ600分别为旋转黏度计3、6、100、200、300、600 r/min的读数；τ为剪切应力，Pa；γ为剪切速率，s-1；τ0为屈服值，Pa；μP为塑性黏度，Pa·s；k为稠度系数，Pa·sn；n为流性指数；τc为卡森屈服值，Pa；μ∞为极限高剪切黏度，mPa·s；τHB为赫巴屈服值，Pa；τi，data为实测剪切力；τi，cal为理论剪切力。

2.2 非线性回归分析新算法

求解非线性最小二乘问题，常使用的是LMF算法[9]，但是在实际应用中发现，如果初始值设置不好，算法常收敛到无意义解。为克服这一弊端，结合赫巴及幂律模式流变方程的特点，提出用0.618法即一维搜索的黄金分割法来计算赫巴模式、幂律模式的流变参数。

设实测数据为(τ1，γ1)，(τ2，γ2)，(τ3，γ3)，…,(τN，γN)，定义最小二乘目标函数F。

赫巴流体：

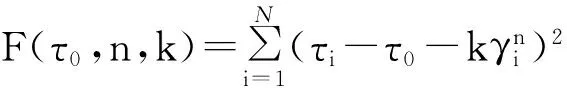
(1)

幂律流体：

(2)

因此，流变参数估计问题可归结为求最小值问题：min[F()]，通过求目标函数的最小值，就可得到2种流变模式流变参数的最优估计值。以幂律模式为例介绍计算流变参数的0.618法。

对式(2)求函数偏导数，得到：

(3)

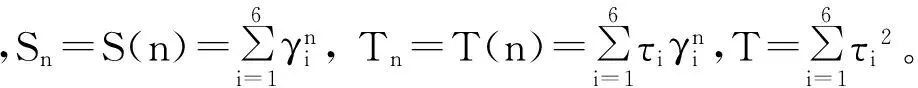
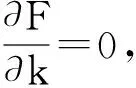
(4)

此时，目标函数可改写为

F(n)=T+k2S2n-2kTn。

(5)

F(n)是关于n的一元函数，当其取得最小值时对应的n值即为最优流性指数值，再由式(4)即可求出最优稠度系数k值。由于现场用钻井液n值多在0到1之间，且 F(n)在区间[0,1]上是下单峰函数[10]，故可用一维搜索方法中的0.618法求其最小值。

0.618法的详细计算步骤如下[11]：

Step1 由初始区间[a1,b1]及精度要求ε>0，计算试算点。

计算F(n1(1))、F(n2(1)),令k=1。

Step2 若bk-ak<ε，停止计算,[ak,bk]中任意点均可以作为所求极小点的近似，否则，当F(n1(k))≤F(n2(k))时转入Step3，当F(n1(k))>F(n2(k))时，转入Step4。

Step3 令ak+1= ak，bk+1=n2(k)，n2(k+1)= n1(k)，n1(k+1)= ak+1+0.382(bk+1- ak+1)，

计算F(n1(k+1))。

Step4 令ak+1= n1(k)，bk+1= bk，n1(k+1)= n2(k)，n2(k+1)= ak+1+0.618(bk+1- ak+1)。

计算F(n2(k+1))。

Step5 令k=k+1，转入Step2。

由此，可得到幂律模式的最优流性指数n值，进而由式(4)求出稠度系数k值。同理对于赫巴模式可先用0.618法求出其n值，然后即可得到其他流变参数值。

该算法具有运行稳定、不用设初始值、循环次数少、计算速度快、易于编程的优点。

3 流变模式的优选

目前，钻井液流变模式的优选方法有以下几种：

(1)图示对比方法

图示对比法是通过绘制钻井液理论流变曲线和实测流变曲线，进行直观曲线拟合比较而确定最优流变模式。

图示法是一种直观定性的优选方法，缺点是具有主观性，计算作图比较繁琐、精度不高，并且当几条曲线彼此接近时，肉眼判断比较困难。

(2)剪切应力误差对比法[12]

该方法是通过对理论剪切应力值与实测剪切应力值进行相对误差和平均相对误差计算，取平均相对误差最小者确定为最优流变模式。

该方法计算十分简单，但缺点是易受异常点干扰而影响判断的准确性。

(3)相关系数法

2个随机变量x与y的线性相关程度可由相关系数R[13]来衡量。其中，0<|R|<1,|R|越接近1则线性关系越强，反之则越弱。

有学者提出用相关系数作为线性流变模式及可化为线性模式的非线性流变模式的优选标准[1,3]。但是上文已指出对非线性流变模式不能采用线性回归分析进行求解。所以用R作为优选标准也就失去了意义。

(4)拟合残差的平方和对比法

首先，定义如下统计量：

拟合残差

ξi=τi，data-τi,cal，

(6)

拟合残差的平方和

(7)

回归分析法计算流变参数都是基于最小二乘方法，即拟合残差的平方和最小。拟合残差的平方和越小，则相关程度越大，表示所用流变方程与实际的实验曲线越接近。所以无论采用线性还是非线性回归，都可采用拟合残差平方和作为优选标准。该方法克服了相关系数法不能评价非线性回归模型的弊端，适用于所有基于最小二乘原理的回归分析方法的评价，简单准确，因此本文将该方法用于流变模式的优选。

4 计算软件开发及实例分析

传统的流变参数计算过程较为简单，手工计算即可满足实际要求。采用回归分析方法若再使用手工计算，不仅计算工作量大，而且易造成人为误差。通过计算机软件的开发能克服手工计算的弊端，而且还确保了计算的精度。

软件编程采用C#语言，在 VS2010平台上开发了钻井液流变模式优选程序。在输入界面上依次输入旋转黏度计的6组数据，程序运行后将会得到各流变模式的流变参数计算结果。软件还可以直接得到与钻井液实际流变性能最为拟合的流变模式。另外也可以根据需要选择指定的流变模式，并得到该流变模式下最优的流变参数。

本文收集了不同配方钻井液的实测数据[2,9,14]来进行算例分析，如表2所示。

图1是用开发的软件计算后得到的不同流变模式残差平方和柱状对比图。从图1可以看出上述5种钻井液采用赫巴模式时，残差平方和是最小的，因此5种钻井液的最佳流变模式均为赫巴模式。

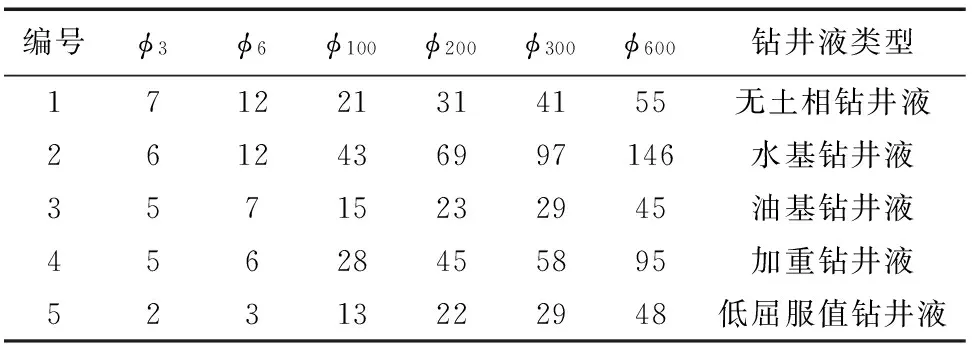
表2 不同配方钻井液实测数据

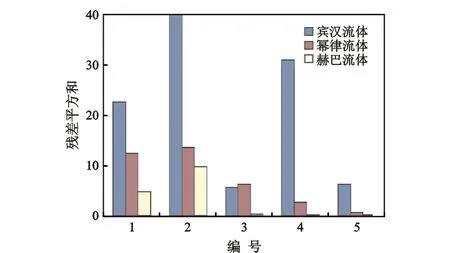
图1 不同流变模式残差平方和柱状对比图

为了对线性回归分析及0.618法非线性回归分析进行对比，本文也采用线性计算方法编制了相应的计算程序。表3是幂律模式线性回归分析及非线性回归分析计算结果对比表。

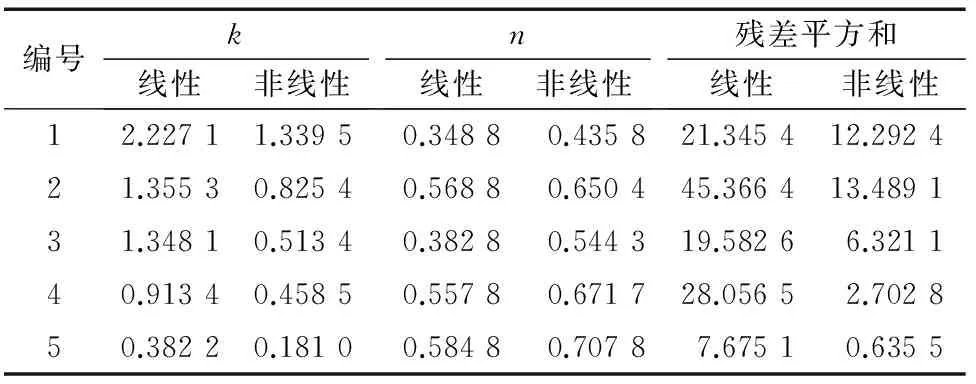
表3 幂律模式线性与非线性回归分析计算结果对比

由表3可以看出0.618法拟合残差的平方和明显低于线性方法，这说明对于非线性流变模式，用线性回归方法所求得的流变参数估计值不是最优的估计值。从对比结果也可以看出本文所用的0.618法的准确性及有效性。

5 结 论

(1)计算钻井液流变参数的常规算法虽然简单易用，但是计算结果误差较大，不利于后续的钻井水力学计算。

(2)拟合残差平方和法克服了相关系数法不能评价非线性回归模型的弊端，适用于所有基于最小二乘原理的回归分析方法，简单有效。

(3)回归分析法计算流变参数可以提高计算精度。非线性流变模式采用线性回归分析方法计算不能得到最优的参数估计，0.618法非线性回归分析可以精确计算常用的幂律流体和赫巴流体的流变参数。通过不同类型钻井液的实例计算表明，0.618法可得到最小二乘意义下流变参数的最优解。

[1] 张辉，樊洪海，逄淑君.钻井液流变参数计算方法及现场应用软件开发[J].西部探矿工程，2008,20(2)：72-73,77. ZHANG Hui,FAN Hong-hai,PANG Shu-jun.Drilling fluid rheological parameter calculation method and field application software development[J].West-China Exploration Engineering,2008,20(2):72-73,77.

[2] 汪海阁，刘希圣.钻井液流变模式比较与优选[J].钻采工艺，1996,19(1)：63-67. WANG Hai-ge,LIU Xi-sheng.The comparison and optimization of drilling fluid rheological mode[J].Drilling & Production Technology,1996,19(1):63-67.

[3] 胡茂焱，尹文斌，郑秀华，等.钻井液流变参数计算软件的开发及流变模式的优化[J].钻井液与完井液，2005,22(1)：28-30. HU Mao-yan,YIN Wen-bin,ZHENG Xiu-hua,et al.A drilling fluid rheological parameter calculation software and the rheological model's optimization[J].Drilling Fluid & Completion Fluid,2005,22(1):28-30.

[4] 周华安.高密度钻井液流变模式及其参数计算方法选择[J].钻采工艺，1995,18(1)：82-85. ZHOU Hua-an.The selection of high density drilling fluid rheological model and its parameter calculation method[J].Drilling & Production Technology,1995,18(1):82-85.

[5] 刘胜，张红梅.最优估计理论[M].北京：科学出版社，2011：40-60.

[6] 胡茂焱，尹文斌，郑秀华，等.钻井液流变参数计算方法的分析及流变模式的优选[J].探矿工程:岩土钻掘工程，2004,31(7)：41-45. HU Mao-yan,YIN Wen-bin,ZHENG Xiu-hua,et al.Analyses on calculation methods of rheological parameters of drilling fluid and optimization of rheological model[J].Exploration Engineering:Rock & Soil Drilling and Tunneling,2004,31(7):41-45.

[7] 董书礼，鄢捷年.利用最小二乘法优选钻井液流变模式[J].石油钻探技术，2000,28(5)：27-29. DONG Shu-li,YAN Jie-nian.Optimization of drilling fluid rheology model using least square fitting method[J].Petroleum Drilling Techniques,2000,28(5):27-29.

[8] 鲁港，李晓光，陈铁铮，等.钻井液卡森模式流变参数非线性最小二乘估计新算法[J].石油学报，2008,29(3)：470-474. LU Gang,LI Xiao-guang,CHEN Tie-zheng,et al.A new method for non-linear least square estimation on rheological parameter in Casson model of drilling fluid[J].Acta Petrolei Sinica,2008,29(3):470-474.

[9] 邓乃扬.无约束最优化计算方法[M].北京：科学出版社，1982：259-295.

[10] 闫吉曾.基于分数法求赫巴模式流变参数最优值[J].重庆科技学院学报:自然科学版，2012,14(6)：183-185. YAN Ji-ceng.Seeking rheological parameters optimal solutions of the Herschel-Buckley model based on fibonacci method[J].Journal of Chongqing University of Science and Technology:Natural Sciences Edition,2012,14(6):183-185.

[11] 邓乃扬.最优化方法[M].沈阳：辽宁教育出版社，1987：35-38.

[12] 周号博，樊洪海，翟应虎，等.四参数模式流变参数准确计算方法及其应用[J].石油学报，2012,33(1)：128-132. ZHOU Hao-bo,FAN Hong-hai,ZHAI Ying-hu,et al.Rheological parameter calculation with a four-parameter model and its application evaluation[J].Acta Petrolei Sinica,2012,33(1):128-132.

[13] 樊洪海，冯广庆，王果，等.一种新的流变模式及其应用性评价[J].中国石油大学学报:自然科学版，2010,34(5)：89-93,99. FAN Hong-hai,FENG Guang-qing,WANG Guo,et al.A new rheological model and its application evaluation[J].Journal of China University of Petroleum:Edition of Natural Science,2010,34(5):89-93,99.

[14] 刘东.幂律钻井液流变参数估计的改进算法[J].江汉石油职工大学学报，2008,21(2)：31-33,40. LIU Dong.An improved algorithm of rheology parameters of power-law drilling fluid[J].Journal of Jianghan Petroleum University of Staff and Workers,2008,21(2):31-33,40.

责任编辑：董 瑾

2014-10-20

国家自然科学基金项目(编号：51074125)

李琪(1963-)，男，教授，博士生导师，主要从事石油钻井信息技术、导向钻井等方面的研究。E-mail：liqi@xsyu.edu.cn

1673-064X(2015)02-0084-04

TE28

A