潮流紊动特性试验研究

赵懿珺，曾 利，贺益英，吴一红

（中国水利水电科学研究院，流域水循环模拟与调控国家重点实验室，北京 100038）

潮流紊动特性试验研究

赵懿珺，曾 利，贺益英，吴一红

（中国水利水电科学研究院，流域水循环模拟与调控国家重点实验室，北京 100038）

开展潮流的紊动特性研究，对于了解潮汐水域泥沙及污染物输运机理、保护生态环境具有重要意义。本文通过水槽试验系统全面地研究了潮位正弦变化的往复流紊动特性随潮变化规律，以100 Hz的高采样频率连续采集主流区测点三维瞬时流速，根据移动平均法及最小二乘原理计算时均流速过程曲线，据此分析了紊动强度及雷诺切应力随潮变化规律、特征潮时概率密度分布与正态分布的差异，以及脉动流速的紊动能谱。研究结果表明，水流纵向流速随潮近似于正弦规律变化；纵向、横向与垂向的相对紊动强度在转潮阶段出现峰值；涨急与落急时段，与纵向脉动流速相关的雷诺切应力相对较大，纵向与垂向脉动流速概率密度分布偏离正态分布；特征潮时的脉动能谱密度均随频率增大而减小，水流能量主要集中在10 Hz以内。

潮流；紊动强度；雷诺应力；概率密度分布；紊动能谱

1 研究背景

随着我国海洋资源开发利用程度不断提高，生态环境影响问题越来越突出。潮流是河口与海湾地区最为普遍的水流运动形式，也是物质输运的载体。潮流具有非恒定紊流的特点，在引潮力作用下，水流在垂直与水平方向产生周期性运动。研究潮流的紊动特性对于了解潮汐水域污染物、泥沙等物质的输运机理，保护海洋生态环境具有重要意义。

水流的紊动特性一直是流体力学研究领域的重点与难点，由于紊动机理复杂，难以获得各紊动参量的理论解析解，通常借助测量仪器采用试验方法进行研究。严格意义上，紊流本身就具有非恒定性。所谓恒定紊流，通常指统计特性不随时间变化、具有平稳随机过程特点的紊流流态。从上世纪七十年代开始，针对矩形明渠恒定均匀紊流开展了大量试验研究［1-10］，后来又有学者陆续进行了弯道［11-12］、渐扩段［13］、复合渠道［14］等边界条件比较复杂的恒定非均匀流紊动特性研究。目前，恒定紊流研究成果已在环境、水利等工程实践中得到广泛应用。自然界中更多的流动呈现非恒定特征，如水流在洪水、波浪、潮汐等作用下的运动，其紊动特征随时间变化较大，属于非平稳随机过程。近二十多年，非恒定紊流引起许多学者的关注，并取得丰富的成果。Nezu（1995，1997）、Song（1996）分别采用二维LDV、ADVP测量了明渠洪水过程中水流的紊动特性，发现涨水段紊动强度和雷诺应力大于落水段；流速及紊动参量随水位涨落表现出绳套变化［15-17］。Carlo和Hubert（2011）对水槽中正向涌浪的试验研究成果表明，随着水位上涨纵向流速迅速下降，雷诺应力在波峰与波谷处出现大值［18］。Hu和Yang等（2012）研究了来流量正弦变化时水槽内的非恒定流动过程，但仅关注波速、波浪变形率等参数，未开展紊动特性研究［19］。已有的非恒定流研究成果，研究对象多为洪水或波浪，而且仅水位及流速值随时间变化，流向不改变。潮流具有周期长、水深及流速随潮变化，并且水流流动方向在涨落潮过程中发生转变的特点。目前，关于潮流紊动特性的系统研究很少，仅有一些零星的原体观测。卢金友（2005）、Liu（2009）、Hubert（2011）、Ni Zhi-hui（2012）对天然感潮河段及海湾水流紊动特性进行测量，发现潮流的紊动强度、雷诺应力等紊动参数的时空分布均与恒定流有所差异［20-23］。天然海湾中水流运动除了受潮汐作用外，还受到岸线、地形、风浪等复杂因素的影响，而且潮周不具有重复性，为此，可通过水槽试验开展潮流紊动特性的基本研究，为系统理论分析提供依据。

对于河口及近岸海域，往复流是常见的潮流运动形式。本文在潮汐水槽上，通过自动生控潮系统产生水位及流速周期性变化的往复潮流，采用ADV超声波流速仪以100 Hz采样频率连续采集水槽中心平均潮位以下二分之一水深处测点的三维瞬时流速，按照移动平均法及最小二乘原理计算时均流速过程，以此为基础分析水流脉动速度、紊动强度、雷诺应力的随潮变化规律，对比涨急、涨憩、落急、落憩四个特征潮时水流脉动实测概率分布与正态分布的差异，并通过离散傅立叶变换分析不同时刻潮流的脉动能谱。

2 试验系统简介

试验系统布置如图1所示。玻璃水槽全长20 m、宽0.6 m、深0.6 m、底坡为0。采用开边界流量控制，监测水位的控潮方式。水槽两侧各布设一台进水泵与一台出水泵，水泵流量可由变频器控制达到无级调节。利用中国水利水电科学研究院自主研发的新型潮汐自动模拟系统，由计算机根据给定的开边界流量过程线自动控制进出流量，实现潮流模拟。

图1 试验系统及测点布置

图2 潮位变化曲线

3 紊动特性分析

3.1 瞬时流速及脉动速度坐标系满足右手定律，x轴平行水槽中轴线，自西向东为正，y轴在水平面上垂直于x轴，z轴垂直向上。采用ADV以100 Hz的采样频率连续采集测点一个潮周的流速，获得纵向x、横向y、垂向z的瞬时流速u、v、w变化过程（图3）。潮流条件下，水流流动属非平稳随机过程，水位及流速为时间变量，瞬时流速具有明显的脉动特性，其变化范围形成带状，带宽反映了脉动幅度。对于非定常流动，应采用系综平均法获得平均流速［25］，但由于实际工作中难以做到足够多次的严格重复试验，因此实施很困难。移动平均法是非恒定紊流中统计平均流速常用的处理方式，该方法用某点及与之相邻的若干点的算术平均值作为该点的平均值［24］。本文考虑到潮周变化过程中在一个微小时段内流动可近似认为局部平稳的随机过程，采用移动平均法沿着数据系列每隔6 s统计一次，每次选择该时刻附近的600个数据点进行计算，以此获得121个时刻的平均流速，再根据最小二乘原理进行拟合，得到图3所示的平均流速、、的随潮变化曲线。纵向流速受潮流影响显著，随潮近于正弦规律变化，但涨、落潮流速不尽相同，最大涨潮流速0.125 m/s、出现在150 s，最大落潮流速-0.115 m/s、出现在534 s，且流速变化与潮位变化存在20～30 s的相位差，涨落潮流速峰值略早于潮位高平、低平出现时刻；横向与垂向流速相对较小，脉动幅度也小。湍流脉动流速。三个方向的脉动流速随潮过程见图4，纵向脉动流速在涨落潮过程中变化显著，幅值总体与流速大小相关，憩流时刻相对较小，涨急与落急时段相对较大，但在水流流向反转时尽管流速接近于零但也出现大值；横向与垂向脉动流速较小，基本在±0.04 m/s范围内变化。

3.2 相对紊动强度及雷诺应力定义 三个方向相对紊动强度，式中特征流速。如图5所示，纵向紊动强度明显大于横向与垂向，除两个峰值附近时段外，涨落潮过程中大部分时刻Iu在0.4～0.5范围内变化、Iv与Iw不到0.16，各方向紊动强度大小的相对关系与恒定流研究成果一致［6］；但潮流条件下，相对紊动强度在转潮过程中受到逆流影响出现峰值。雷诺应力的物理意义是紊动所产生的动量传递［25］，正应力变化规律与紊动强度一致，本文重点分析切应力，其表达式为。图6表明，与纵向相关的雷诺切应力与非恒定特征比较明显，涨急与落急时段相对较大、憩流时段相对较小。

3.3 脉动速度概率分布脉动流速的概率分布在恒定均匀紊流中接近正态分布，在非恒定流中与正态分布有所偏离，这一现象已在许多文献中有所论述［6，20，24］。针对四个特征潮时涨急150 s、涨憩354 s、落急534 s、落憩690 s，以600点样本容量进行统计，求取各流速区间内流速出现的概率，点绘频率曲线。同时，按照式（1）计算变量m（m分别为u′、v′、w′）的正态分布概率密度函数，并绘制理论概率分布曲线。从图7两种曲线的对比结果可以看出，纵向脉动流速u′在潮流较强时，概率分布不符合正态分布，涨急时段频率峰值所在的流速区间出现正偏、落急时段出现负偏；横向脉动流速v′的概率分布基本符合正态分布；垂向脉动流速w′的概率分布受潮位涨落也表现出与正态分布的偏离。

图5 紊动强度变化过程

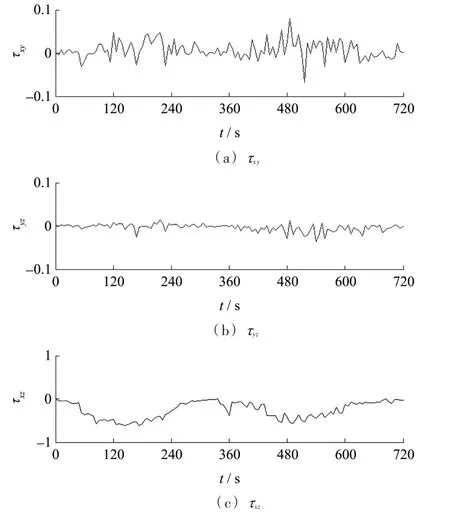
图6 雷诺应力变化过程

图7 特征潮时脉动流速实测频率分布与理论概率分布对比

3.4 能谱密度紊流由许多大小不同的涡旋组成，能谱反映了不同尺度涡旋脉动能量的分布。采用经典谱估计中性能较好的Welch方法［12］进行离散傅立叶变换，将特征潮时的脉动流速从时域转换到频域。图8显示，涨急、涨憩、落急、落憩四个特征潮时的能谱密度Sf均随频率f增大而衰减，绝大部分能量集中在10 Hz以内；从三个方向的能谱曲线差异看，纵向脉动流速在低频区域的能量更为集中，而横向和垂向脉动流速由于紊动周期更短，高频区域的能量相对较多。

4 结论

图8 紊动能谱

本文全面系统研究了潮流条件下水流的紊动特性，为了解河口、海洋等潮汐水域泥沙及污染物输运机理奠定了基础。研究结果表明，涨落潮过程受水位、流速、流向变化影响，水流各项紊动参数表现出区别于恒定流的特点。纵向平均流速随潮近似于正弦变化规律，但涨落潮流速峰值出现时刻略早于高平、低平时刻；脉动流速在流动转向及潮流较强的时段幅值较大；相对紊动强度在潮流逆转时出现峰值；与纵向脉动流速相关的雷诺切应力涨急与落急时段相对较大、憩流时段相对较小；脉动流速的概率分布，除横向接近正态分布外，纵向与垂向均表现出与正态分布的偏离；特征潮时的脉动能谱密度均随频率增大而衰减，绝大部分能量集中在10 Hz以内。

［ 1］ Grass A J.Structural features of turbulent flow over smooth and rough boundaries［J］.Journal of Fluid Mechanics，1971，50：233-255.

［ 2］ Nezu I，Rodi W.Open-channel flow measurements with a Laser Doppler Anemometer［J］.Journal of Hydraulic Engineering-ASCE，1986，112（5）：335-355.

［ 3］ Kirkgoz M S.Turbulent velocity profiles for smooth and rough open channel flow［J］.Journal of Hydraulic Engi⁃neering-ASCE，1989，115（11）：1543-1561.

［ 4］ Lhermitte R，Lemmin U.Open-channel flow and turbulence measurement by high-resolution Doppler Sonar［J］. Journal of Atmospheric and Oceanic Technology，1994，11（5）：1295-1308.

［ 5］ 林鹏，陈立.低含沙水流紊动结构的实验研究［J］.水动力研究与进展：A辑，2003，18（2）：209-216.

［ 6］ 刘艾明，徐海涛，卢金友.矩形水槽水流紊动特性分析［J］.长江科学院院报，2006，23（1）：12-15.

［ 7］ Chanson H，Carosi G.Turbulent time and length scale measurement in high-velocity open channel flows［J］.Ex⁃periments in Fluids，2007，42（3）：385-401.

［ 8］ 刘丽，杨成渝，何光春，等 .清水紊流流速脉动的谱分析［J］.重庆交通大学学报：自然科学版，2008，27（3）：460-462.

［ 9］ Omer KOSE.Distribution of turbulence statistics in open-channel flow［J］.International Journal of the Physical Sciences，2011，6（14）：3426-3436.

［10］ Pechlivanidis G I，Keramaris E，Pechlivanidis I G，et al.Measuring the turbulent characteristics in an open chan⁃nel using the PIV method［J］.Global NEST Journal，2012，14（3）：378-385.

［11］ Blanckaert K，VriendH J.Turbulence characteristics in sharp open-channel bends［J］.Physics of Fluids，2005，17（5）：005102.

［12］ 王虹，王连接，邵学军，等.连续弯道水流紊动特性试验研究［J］.力学学报，2013，45（4）：525-533.

［13］ 童思陈，王亮，郭荣.渐扩段水流紊动特性试验研究［J］.水力发电学报，2013，32（5）：109-114.

［14］ Koziol A P.Turbulent kinetic energy of water in a compound channel［R］.Annals of Warsaw University of Life Sciences-SGGW，2011，43（2）：193-205.

［15］ Nezu I，Nakagawa H.Turbulence measurements in unsteady free-surface flows［J］.Flow Measurement and In⁃strumentation，1995，6（1）：49-59.

［16］ Nezu I，Kadota A，Nakagawa H.Turbulent structure in unsteady depth-varying open-channel flows［J］.Journalof Hydraulic Engineering.-ASCE，1997，123（9）：752-763.

［17］ Song T，Graf W H.Velocity and turbulence distribution in unsteady open-channel flows［J］.Journal of Hydraulic Engineering，1996，122（3）：141-154.

［18］ Carlo Gualtieri，Hubert Chanson.Experimental study of a positive surge.Part 2：comparison with literature theo⁃ries and unsteady flow field analysis［J］.Environmental Fluid Mechanics，2011，11（6）：641-651.

［19］ Jiang Hu，Sheng Fa Yang，Xu Hui Fu.Experimental investigation on propagating characteristics of sinusoidal un⁃steady flow in open-channel with smooth bed［J］.Science China Technological Sciences，2012，55（7）：2028-2038.

［20］ 卢金友，徐海涛，姚仕明.天然感潮河道水流紊动特性分析［J］.海洋工程，2005，23（3）：70-77.

［21］ Liu Huan，Wu Chaoyu，Xu Weiming，et al.Contrast between estuarine and river systems in near-bed turbulent flows in the Zhujiang（Pearl River）Estuary China［J］.Estuarine，Coastal and Shelf Science，2009，83（4）：591-601.

［22］ Hubert Chanson，Richard Brown，Mark Trevethan.Turbulence measurements in a small subtropical estuary un⁃der king tide conditions［J］.Environmental Fluid Mechanics，2011，12（3）：265-289.

［23］ Ni Zhi-hui，Song Zhi-yao，Zhang Xu-jin，et al.A modification to vertical distribution of tidal flow Reynolds Stress in shallow sea［J］.China Ocean Engineering，2012，26（3）：431-442.

［24］ 刘春晶.明渠非恒定流运动规律及推移质输沙特性的试验研究［D］.北京：清华大学，2004.

［25］ 余常昭.环境流体力学导论［M］.北京：清华大学出版社，1998：54-55.

Experimental study on turbulent characteristics of tidal flow

ZHAO Yijun，ZENG Li，HE Yiying，WU Yihong
（State Key Laboratory of Simulation and Regulation of Water Cycle in River Basin，China Institute of Water Resources and Hydropower Research，Beijing 100038，China）

Study on turbulent characteristics of tidal flow is essential to understand the mechanism of con⁃taminant and sediment transport，as well as ecological and environmental protection in tide water.A system⁃atic overall analysis was performed for the variation of turbulence in a tidal flow with sinusoidal water lev⁃el.Three-dimensional instantaneous velocity of a point in the mainstream region was sampled continuously with high sampling frequency of 100 Hz.The evolution of turbulent intensity and Reynolds shear stress，the difference between measured probability density distribution and normal distribution at typical moments，as well as turbulent energyspectrum of fluctuating velocity wereanalyzed，based on the mean velocity calculated by a moving average method and principle of least squares.Results show that the longitudinal velocity changes approximately in according to sinusoidal curve，the peak values of relative turbulent intensity in the longitudinal，lateral，and vertical directions occur at the transitional stage of tides.Results also show that for flood tide and ebb tide，Reynolds shear stress associated with longitudinal turbulent velocity enhances and the probability distribution of longitudinal and vertical fluctuating velocity deviates from the normal dis⁃tribution.It is also found that the density of turbulent energy spectra decreases with the increase of frequen⁃cy，and the main frequency is below 10 Hz for energy of water flow.

tidal flow；turbulent intensity；Reynolds stress；probability density distribution；energy spectra

TV131.66

：Adoi：10.13244/j.cnki.jiwhr.2015.01.001

1672-3031（2015）01-0003-06

（责任编辑：李福田）

2014-11-25

国家自然科学基金资助项目（51309257）；中国水利水电科学研究院科研专项（水集1447）

赵懿珺（1975-），女，山西人，博士生，高级工程师，主要从事环境水力学研究。E-mail：yijunzhao2012@163.com