系杆拱桥吊杆初张力的确定方法及试验研究

徐 伟

(湖南省交通规划勘察设计院，湖南 长沙 410008)

0 引言

随着经济的发展，人们对生活环境的舒适度和美观性要求日益提升。在公路建设项目中，下承式系杆拱桥自身具有外形优美，可以取消横撑等优势在道桥建设中应用十分广泛，施工时通常采用搭架现浇的方式。下承式系杆拱桥具有下述两方面特点:第一，外部静定，内部超静定;第二，主梁属于拉弯受力构件。吊杆为受拉构件，普遍采用高强钢丝或钢铰线。吊杆拉力的大小对结构内力的影响非常大，因此存在一个如何确定吊杆初张力的问题，不同的初始拉力大小将导致不同的结构内力分布，其重要性不言而喻。

对于下承式系杆拱桥吊杆索力的确定，可以归纳为两种方法:一种是最优索力法，从主梁和拱圈受力角度出发，通过调整吊杆索力的大小，尽量减小两者的内力，目标是结构弯矩应变能最小，类似于斜拉桥结构的索力优化［1－3］，优点是结构内力分布得到了极大的改善;但由于在施工过程中结构体系一直在变化，使得调索施工过程过于复杂，不便于实用，本文提出一个便于工程应用的新方法。另一种则是基本上不进行张拉、或张拉力非常小，旨在将吊杆挂在拱圈和主梁上并将其拉直即可，优点是大大简化了吊杆索力调整的施工过程、更简化了设计计算过程;缺点是主梁在恒载作用下的弯矩内力非常大，需要布置非常多的预应力筋，以满足结构受力的需要，造成了一定的材料浪费，同时预应力的张拉过程需要进行详细的设计［4－7］。

本文以一整体式现浇下承式拱桥为分析对象，分别阐述了两种不同方法的分析过程以及可能存在的问题，并推导了有关计算公式。

1 工程案例

某高速公路分离式采用下承式拱桥:长度78 m，矢跨比为1/5;整个建设项目中共包括11 对吊杆，每个吊杆的高强钢丝参数为61Ф7;施工方式为搭架现浇;整体结构施工顺序为:主梁→拱圈→张拉吊杆。详细结构示意图如图1 所示。

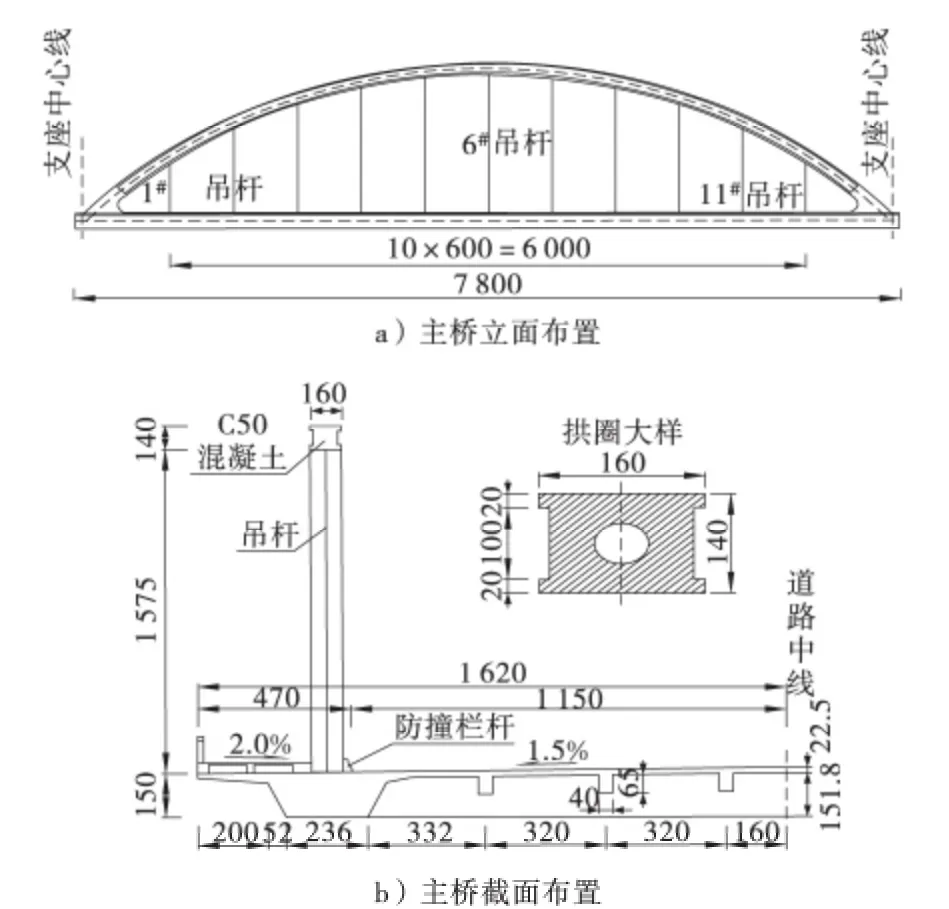
图1 主桥结构示意图(单位:cm)

2 方法一:最优索力法

2.1 分析目的

吊杆索力采用一次张拉到位(之后不再进行调整)、并使结构内力分布最优。要同时达到这两个目的，认为是主梁和拱圈在浇注完成后(结构上作用一期恒载)，张拉吊杆至一个合适的索力大小、使主梁刚刚脱离支架为限。

2.2 分析理论

如图2 所示，假设拱桥结构中共有n 对吊杆，主梁、拱圈浇注完混凝土后，主梁支撑在支架上、拱的支架拆除。此时张拉其中一根吊杆j 时(单位张拉力)，对任意一根己张拉吊杆i 位置处主梁的支撑反力产生一个影响系数aij。具体含义可参见图2。

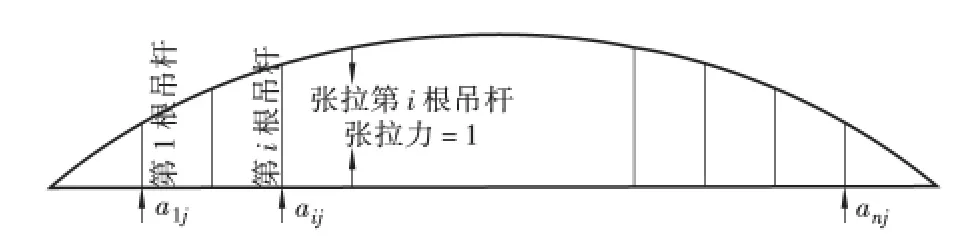
图2 影响系数aij的示意

按照施工顺序依次张拉其它吊杆，这样张拉完全部吊杆后可以产生一个影响矩阵［A］，定义如下:

其中:影响矩阵:

吊杆初张力增量列阵:

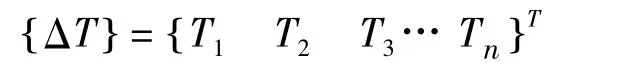
吊杆支撑处反力列阵:

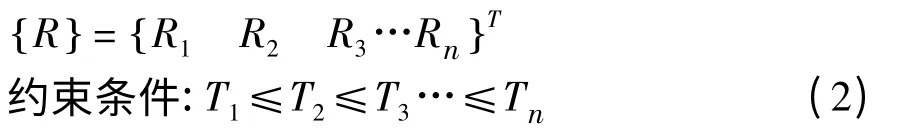
其中:约束条件的目的是保证各拉索受力大小基本相同;列阵{ R} 为全部吊杆张拉完成后主梁支撑在之间上各吊杆位置处的反力大小，和矩阵［A］一样均可以通过桥梁分析软件摸拟拱桥的施工过程得到。

2.3 方程求解

根据本例的结构布置，吊杆共11 对，通过模拟大桥的施工过程计算得到列阵{ R} 和矩阵{ A}。吊杆采用从边杆到中杆、纵向采用对称张拉时，通过调整公式(1)中的方程，未知数可以减少为6。假设初张力为1 000 kN，通过模拟施工过程，计算得到:

此时可求解方程组(1)。方程组的求解方法有两个:

1)考虑约束条件，利用线性规划法进行求解得到初张力增量 {Δ T }，与初张力叠加后得到最终的吊杆初张力值:

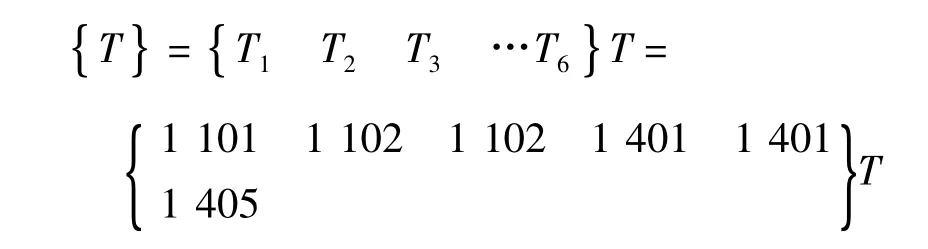
此索力即为张拉时的最优索力。最终的结构内力须根据此索力按照施工过程进行分析得到。最终的结构弯矩图见图3。

2)不考虑约束条件(2)，直接求解线性方程组［A］{ ΔT }={ R}，可以得到初力增量，与初张力叠加得到最终的吊杆初张力值:

由此也可以进行结构的内力计算，内力结果与考虑约束条件的情形基本一致。

2.4 讨论

综上所述，采用最优索力法具有下述几方面优势:第一，施工简单;第二，理论计算过程中考虑到其他各种因素对结构的影响，例如:拱、梁的弯曲、吊杆的弹性变形等;第三，由于系杆在结构处不受任何支撑反力，因而也不会发生形变，所以符合结构弯曲内力值最小的原则。

3 方法二:吊杆不张拉

宗旨是:吊杆张拉过程中只是将吊杆张拉一个很小的力，目的是将吊杆拉直，之后也不再对吊杆进行补张拉。显然按这种方法施工不存在调索过程、施工和计算简便。但在这种情况下，当主梁产生较大的变形后吊杆开始受力，因而主梁将承受很大的弯矩。很明显，这种方法的施工和计算简便是以增大结构受力为代价的，主梁内须布置较多的预应力以满足结构受力的需要。

4 两个方法导致的内力结果比较

4.1 拱和梁的弯矩比较

分别按照方法一和方法二对本例进行计算，结构恒载弯矩结果列于图3 中。

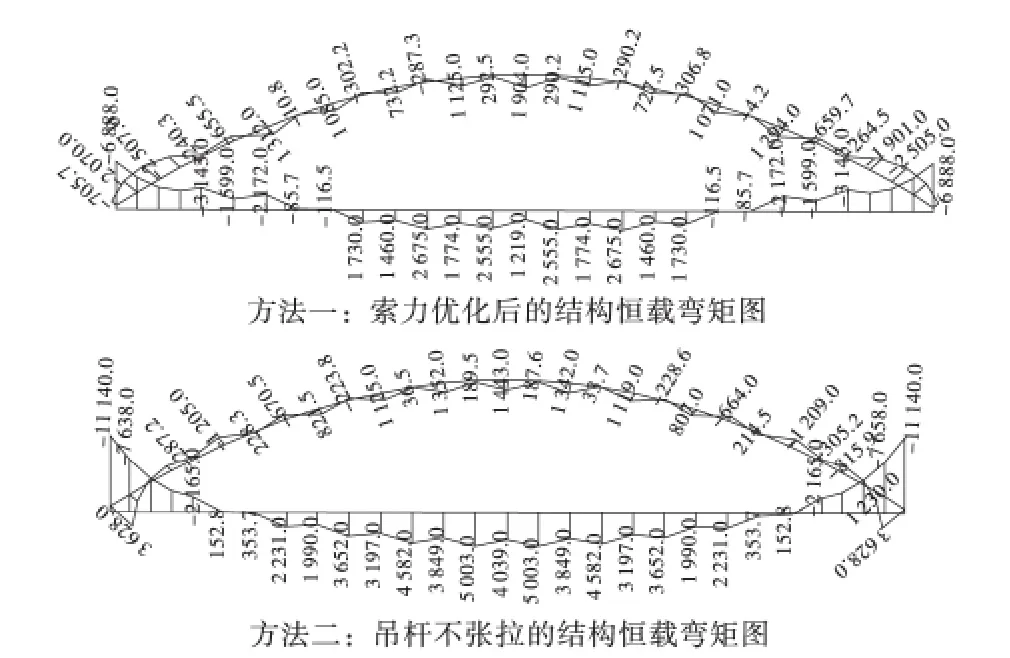
图3 两种方法导致的结构内力结果(单位:kN·m)

4.2 吊杆的轴力比较(表1)

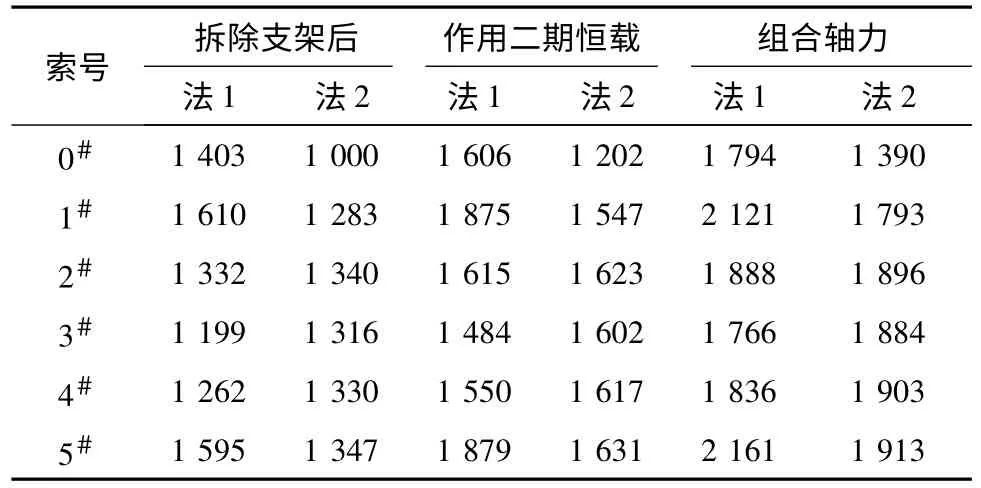
表1 两种方法的索力结果比较 kN

4.3 结果分析

1)两种方法对主梁的恒载弯矩影响比较大。方法一(最优索力法)得到的主梁支点负弯矩为6 888 kN·m，跨中最大正弯矩为2 675 kN·m。而方法二(不张拉)得到的主梁支点负弯矩为11 140 kN·m，跨中最大正弯矩为5 003 kN·m。恒载作用下方法一的最大负(正)弯矩值分别是方法二的61.83%和53.47%。由此可见，通过索力优化后，主梁的恒载弯矩大大减少、组合弯矩也大大减小，这对结构受力和配筋是十分有利的。

2)活载产生的主梁支点负弯矩和跨中正弯矩分别为1 364 kN·m 和2 667 kN·m。显然恒载弯矩远比活载弯矩大。

3)两种方法对拱的受力影响不大。

4)两种方法对靠近拱脚位置的吊杆受力影响较大，但对跨中位置的吊杆影响很小。

5 实验研究

对于本桥，选用方法二(吊杆不张拉，张拉力仅为120 kN)，结构内力结果列于图3。为抵消结构恒载和活载的作用，主梁中布置了大量的纵向预应力(每侧主梁398 根直径15.24 钢绞线)、且全部集中在两侧梁端锚固，如图4 所示。为保证结构安全，在施工过程中对索力进行了监控。

图4 主梁预应力布置

5.1 测点布置

在大桥下游测的1#、6#和11#吊杆锚头下布置了大吨位压力传感器，以测试其索力在施工过程中的变化情况。

5.2 索力实测结果与理论值的比较

表2 为3 根吊杆的索力实测值与理论值的比较。

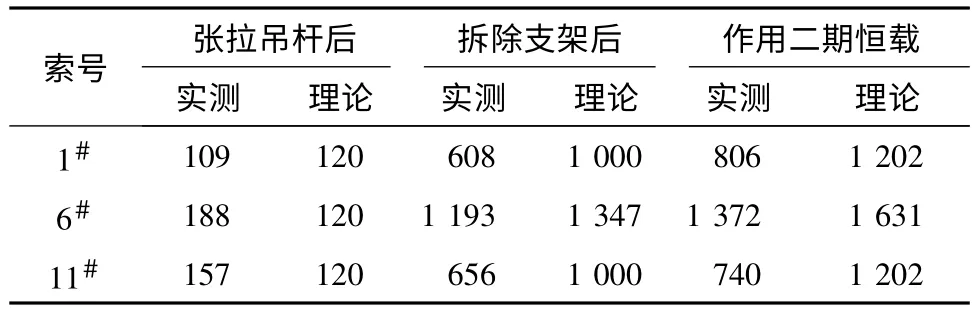
表2 3 根吊杆的索力结果 kN

支架全部拆除完成之后，跨中位置的吊杆索力测试值与理论值基本相近，但在根部截面的吊杆索力测试值普遍要小于理论值(分析原因是拱梁接合部位结构钢度较大，杆系模型无法准确模拟，导致出现误差)。

5.3 主梁受力分析

在该桥的施工过程中，由于没有考虑到梁内布置的预应力是分别抵消不同阶段施加的荷载作用，在向未拆除支架时张拉了全部的预应力筋。由于预应力全部锚固在梁端、应力过于集中，导致全桥4 个靠近拱梁接合部位的桥面板(见图5)均出现了大量典型的、规律的斜裂缝，裂缝贯穿桥面板。显然这是由于预应力过大、且过于集中导致主拉应力过大而引起结构开裂。若在施工过程中，通过分析结构体系荷载的施加情况而逐渐施加预应力，这种裂缝是可以避免的。

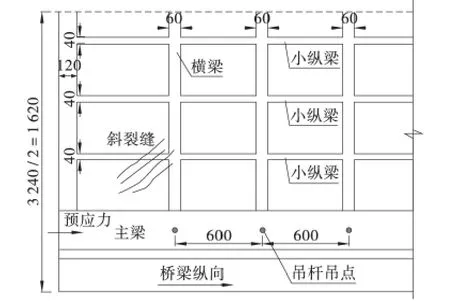
图5 梁端预应力过大、过分集中导致的斜裂缝(单位:cm)

6 结论

对于下承式系杆拱桥吊杆初张力的计算，提出了两种方法:最优索力法和吊杆不张拉法，通过理论和工程实例分析比较研究，得出下述结论:

1)最优索力法。具体计算理论如下:在下承式系杆拱桥的主梁和拱圈施工结束后，根据系杆支撑反力为零及一次张拉的原则，得出具体的计算公式，根据此公式能计算出吊杆的最优索力值。最优索力法的分析和计算过程相对简单，可通过平面杆系模型进行直观、简单的分析，然后再通过线性方程组进行计算，就能很简便的得到索力值;根据计算结果，能使下承式系杆拱桥的结构内力很好的实现均匀分布。同时由于最优索力法计算和分析过程简单，很容易掌握，因此在实际工程项目中可推广使用。

2)吊杆不张拉方法。采用此种计算方法，下承式系杆拱桥中的吊杆几乎不进行张拉，这样对整个桥梁结构来说，主要受力的构件为主梁和拱圈，因此在设计时，主梁构件必须布置许多预应力筋，同时在具体计算过程中，要按照结构重量的具体状况逐步张拉预应力筋，尽量防止一次张拉完所有预应力筋从而造成局部应力过于集中的状况，因为一旦出现局部应力过于集中，就很可能使桥梁主体结构出现开裂。

3)在设计分析中，方法一比较适用于强梁强拱的结构体系(可以对梁和拱的内力同时进行调整);而方法二比较适合于强梁弱拱的结构体系(不能过多的调整拱的内力)。

4)就下承式系杆拱桥而言，结构中系杆布置预应力的主要作用是抵消施工过程中一、二期恒载和活载的作用。在具体施工过程中，结构体系与荷载是逐步形成的，所以系杆的预应力也要逐步增大。具体施工过程，可按照下述步骤进行(如图6)。

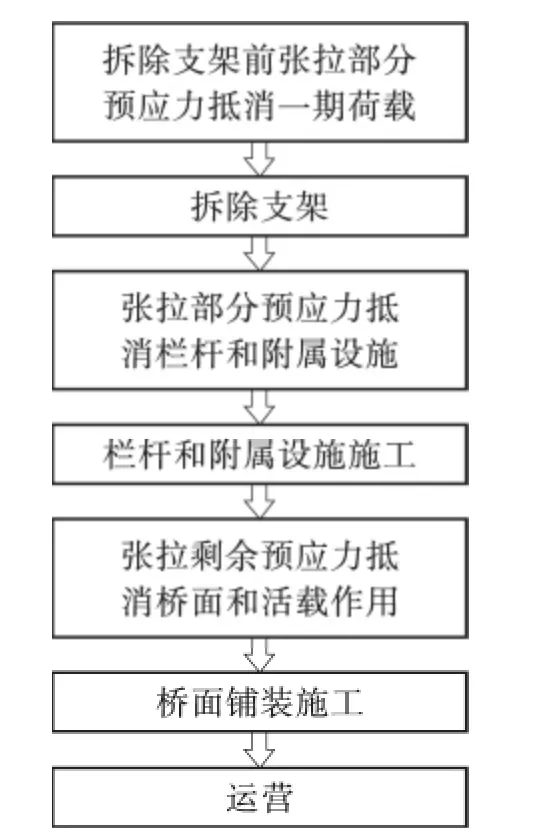
图6 科学施工步骤

［1］肖汝诚，项海帆.斜拉桥索力优化及其工程应用［J］.计算力学学报，1998，15(1):118－126.

［2］虞建成，邵荣光，等.系杆拱桥吊杆初始张拉力及施工控制［J］.东南大学学报，1998，28(3):112－116.

［3］陶 海，沈祥福.斜拉桥索力优化的强次可行序列二次规划法［J］.力学学报，2006，358(3):381－384.

［4］童 林.最小弯曲能量原理在确定拱梁组合体系吊杆成桥张拉力中的研究［J］.公路工程，2011，36(4):68－71.

［5］施静娴，冉志红，谢名娥，等.混凝土收缩徐变效应对矮塔斜拉桥索力的影响［J］.公路工程，2014，39(1):14－18.

［6］蒋建武，朱冠华.系杆拱桥中横梁预制吊装施工新技术［J］.公路工程，2011，36(6):112－115.

［7］王 刚，彭 献.预应力混凝土系杆拱桥动载试验评定分析［J］.公路工程，2013，38(5):38－43.