常规大跨斜拉桥常遇与极端静风荷载响应分析

梁晓晔

(山西省公路局 长治分局，山西 长治 046000)

0 引言

大跨桥梁主梁结构纤细，刚度相对较小，风荷载效应较为突出，研究强风荷载作用下的大跨桥梁响应具有重要的理论与现实意义。根据我国现行桥梁抗风规范规定，主跨跨径大于400 m 的斜拉桥应该计算其静力稳定性［1］。

大跨桥梁抗风研究内容丰富，在静风荷载研究方面主要集中于静风稳定性方向。程进较早系统研究了大跨桥梁的静风稳定性，考虑静风荷载与结构双重非线性影响，基于增量与内外两重迭代完成了大跨径斜拉桥静风稳定性的全过程分析［2］。此外，很多学者对大跨桥梁静风稳定性分析方面进行了广泛研究。李俊对宜宾长江大桥进行了静风稳定性分析［3］;熊正元讨论了静风荷载非线性、初始攻角等影响参数对大跨斜拉桥静风失稳临界风速的影响［4］;杨上清利用ANSYS 分析软件，研究了风速逐级增加的过程中，非线性对静风稳定的影响［5］;邹小江针对大跨度桥梁存在静风失稳的可能性，建立了大跨度斜拉桥非线性静风稳定分析的增量双重迭代搜索法［6］;康小方基于伯努利方程推导了整个断面的三方向静风荷载原理，并采用内外增量双重迭代分析了某跨江大跨度斜拉桥的横桥向风荷载和竖桥向风荷载的影响，并进行成桥状态静风荷载下的特性分析［7］;朱志虎以东海大桥主航道桥为研究对象，对其风振响应进行了深入研究［8］;张德铭对3 座独联体斜拉桥斜拉索抗风减振设施进行了分析，研究了风荷载对斜拉桥的影响［9］;陈海兵通过空间应力分析，探索了不同部位的应力变化过程和分布情况，并指明了应力集中部位，这对于静风荷载响应分析提供了具体截面指导［10］;葛耀君通过各种现代风洞试验方法，检验了某主通航孔斜拉桥结构的抗风稳定性能［11］;黄融结合上海东海地区风环境特点对东海大桥主航道桥进行了静风稳定性数值分析［12］;梁柱针对深圳湾跨海大桥处得出了风场参数与静风稳定性的关系［13］;杨琪建立了完善的大跨度斜拉桥空间线性、几何非线性有限元仿真分析模型，成功实现了桥梁结构分析图形的真三维显示，很好地解决了桥梁结构分析批量数量可视化，为使用数值分析软件进行静风荷载响应分析提供了理论支持［14］;胡晓伦也对大跨斜拉桥的静风稳定性及其影响因素进行了系统研究［15］。

大跨桥梁抗风研究内容详致，类别丰富，本文仅就某特定常规大跨斜拉桥的静风荷载响应进行分析，考虑常遇风速与极端风速两种工况对比分析两者的异同，并给出具体建议。

1 斜拉桥概况

本文选取的大跨斜拉桥具有一定代表性，大桥立面结构如图1 所示，结构型式为5 跨连续半漂浮体系，主跨为448 m，钻石型双塔混凝土桥塔，主塔高度为181.3 m，斜拉索为扇形体系，全桥有56 对索，最大索为248 m 左右，大桥采用空间双索面，拉索顺桥向间距除塔处22.5 m 外，其余均为15 m。加劲梁为带风嘴的栓焊流线型扁平闭口钢箱梁，加劲梁标准横断面如图2 所示，梁高3.5 m，梁宽37.1 m，梁底倾角为20°。

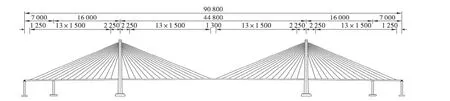
图1 斜拉桥立面图(单位:cm)

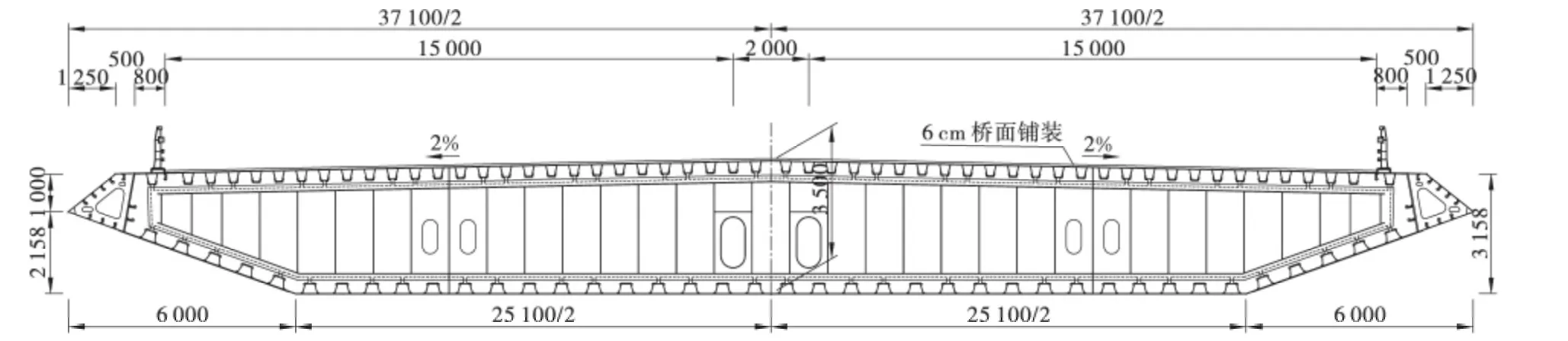
图2 钢箱梁标准断面图(单位:mm)

2 有限元模型与计算参数

2.1 有限元模型

采用离散结构的有限元方法对大桥进行结构建模，根据桥梁总体布置与整体结构特点，保证质量和刚度与实际结构一致的前提下进行适当简化，建立空间杆系有限元模型。有限元模型如图3 所示。

图3 全桥有限元模型

主梁采用单脊梁式，双索面拉索与主梁通过刚臂连接形成“鱼骨式”力学计算模型。采用空间梁单元来模拟主梁、横梁、索塔、过渡墩、承台、刚臂等;采用空间杆单元来模拟斜拉索;采用质量点单元来模拟防撞护栏、桥面铺装、栏杆等二期恒载。整个结构的约束条件与设计要求一致，塔墩在承台顶面作固结处理。

2.2 静力风荷载与分析参数

按照空间3 个主要方向，静力风荷载可以分为静风阻力、静风升力以及静风升力矩。静风三分力荷载可以表示为风速、静力三分力系数及有效风攻角等参数的函数关系，其具体公式如式(1)［16］。

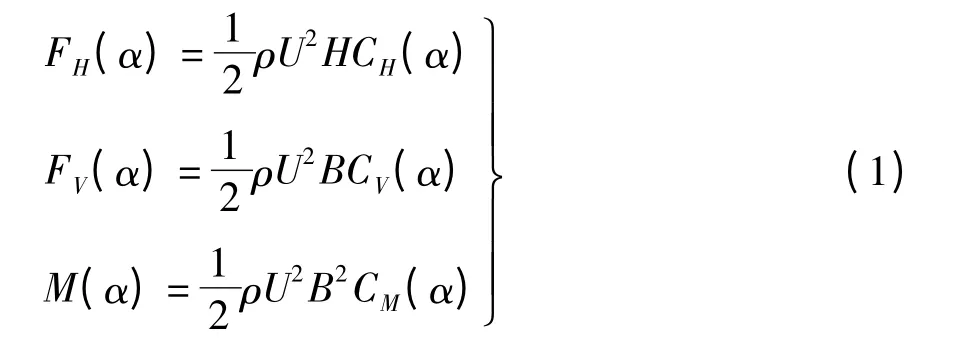
考虑到静风荷载随高度变化而变化，关于不同高度处的静风荷载计算方法主要有两种，指数计算公式与对数计算公式，本文基于指数计算公式确定结构不同高度处的静风荷载，计算公式为式(2)［17，18］。

式中:α 为风剖面指数;zr为参考高度;Ur为在参考高度zr处的风速。

大桥地处我国东南沿海大风区，考虑桥位处常遇风速与极端风速两种工况，根据常年风观测资料，确定常遇风速标准为主梁高度处风速25 m/s，确定极端风速标准为主梁高度处风速49 m/s。

本文取计算风攻角为0°，具体分析参数如表1所示。

3 静风荷载响应

本文除了考虑主梁的静风三分力荷载外，还综合考虑了桥塔与斜拉索结构的静风阻力荷载，将每根斜拉索的静风阻力平分给桥塔与主梁的相应节点处。根据桥梁各构件高度与风剖面指数公式确定主梁、桥塔等各结构的静风荷载，其中桥塔和斜拉索阻力系数根据我国现行抗风规范规定取值，采用集中力加载型式，加载示意图如图4 所示。

图4 静风荷载加载示意图

3.1 位移响应分析

应用有限元分析方法对该桥成桥状态进行了上述常遇与极端两种风速下的静风荷载响应分析，图5 给出了主梁的横桥向位移、竖桥向位移与扭转角位移在两者风速下的对比情况。

由图5a 可知，风速越大，横桥向位移越大。主梁最大横桥向位移发生在中跨跨中处，梁端处横桥向位移较小，风速为25 m/s 时，中跨跨中最大横桥向位移为0.015 m;风速为49 m/s 时，其最大横桥向位移为0.058 m，两者比值约为0.26。由于中跨跨中无斜拉索约束等原因导致跨中刚度相对较小，因此横桥向位移最大，而边跨受到桥塔处和辅助墩的支座约束，横桥向位移较小。

由图5b 可知，主梁最大竖桥向位移也发生在中跨跨中处，边跨处竖向位移基本为0。风速为25 m/s 时，中跨跨中最大竖向位移为0.002 8 m;风速为49 m/s 时，其最大竖桥向位移为0.011 m，两者比值约为0.25。

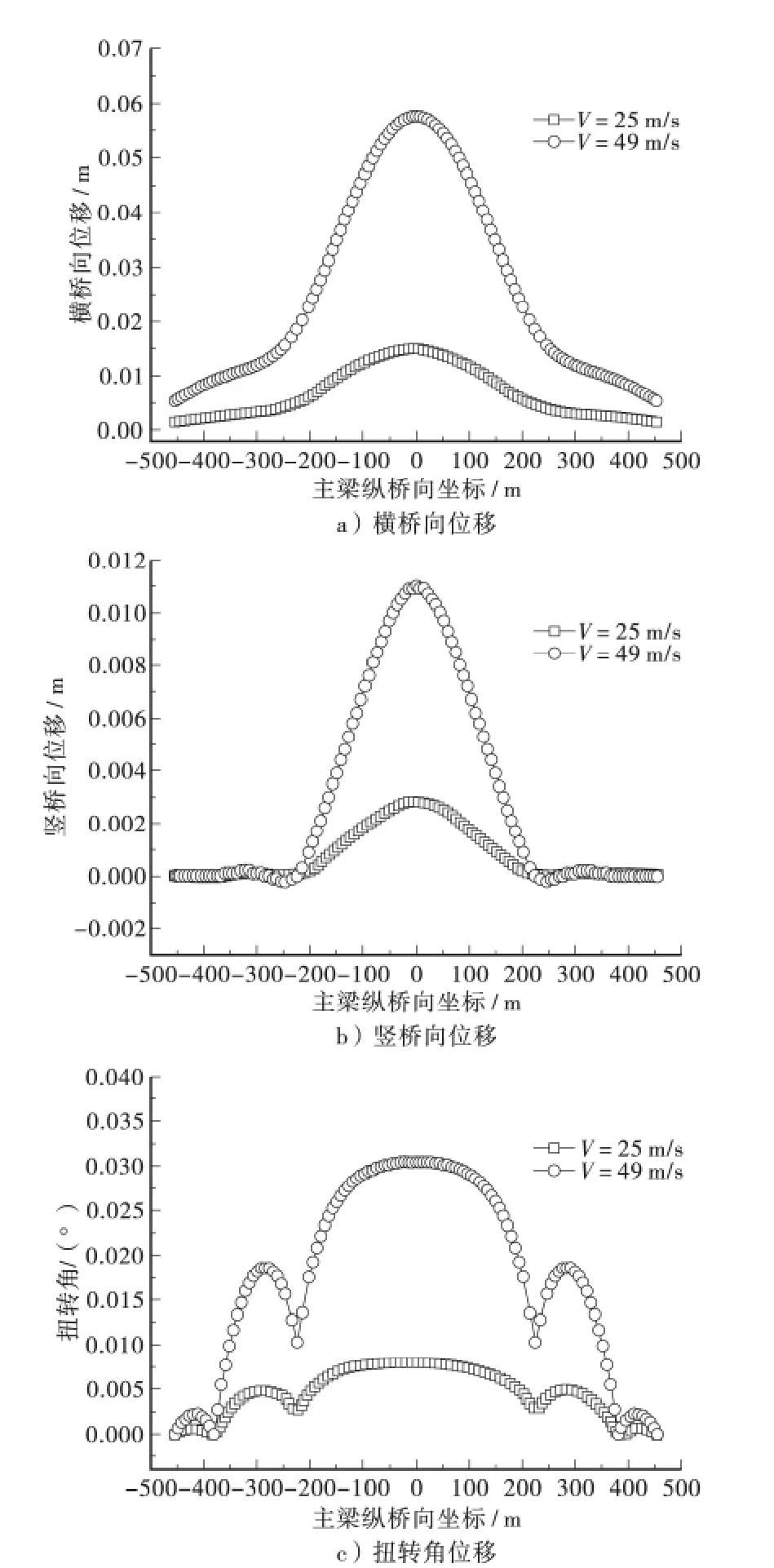
图5 主梁三向位移对比

由图5c 可知，主梁最大扭转角位移同样发生在中跨跨中处，风速为25 m/s 时，中跨跨中最大扭转角位移为0.008°;风速为49 m/s 时，中跨跨中最大扭转角位移为0.030 5°，两者比值约为0.26。值得注意的是，与横桥向和竖桥向位移沿桥跨的变化规律不同，扭转角位移除了在中跨跨中出现峰值外，在两边跨跨中也出现了峰值。

3.2 内力响应分析

通过计算分析，图6 给出了主梁的横向剪力、竖向剪力与扭矩在常遇与极端风速下的对比情况。

由图6a 可知，主梁横向剪力在每一跨内的剪力成线性分布，最大值出现在塔梁交接处，也就是边跨与中跨的分界截面处。中跨跨中与边跨辅助墩截面处横向剪力接近为0。对比两种计算风速下的横桥向剪力发现其比值约为0.26。

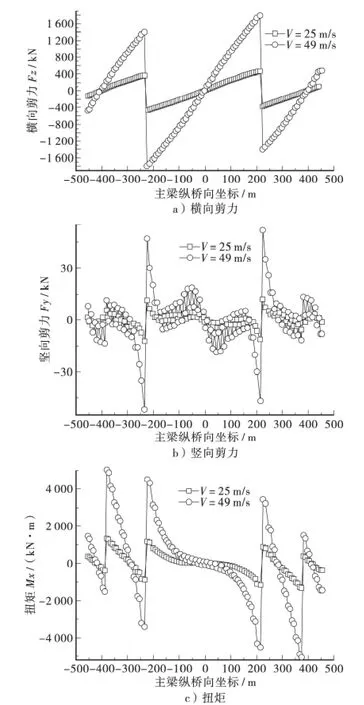
图6 主梁三向内力对比

由图6b 可知，主梁竖向剪力最大值同样出现在塔梁交接处，而且除此截面之外，其他截面的竖向剪力均较小，在中跨跨中与边跨辅助墩截面处竖向剪力接近为0。竖向剪力由于受斜拉索影响较大，在斜拉索布置区域的竖向剪力呈锯齿形分布。对比关键截面处两种风速下的竖向剪力比值发现集中在0.23 ～0.24 之间。

由图6c 可知，主梁最大扭矩出现在边跨辅助墩截面处，塔梁交界处也出现较大峰值，其他截面处扭矩较小，中跨跨中截面处的扭矩接近为0。表2 给出了数个关键节点处计算扭矩值在两种风速下的比值，由表2 可知，两种计算风速下的扭矩比值约为0.26。

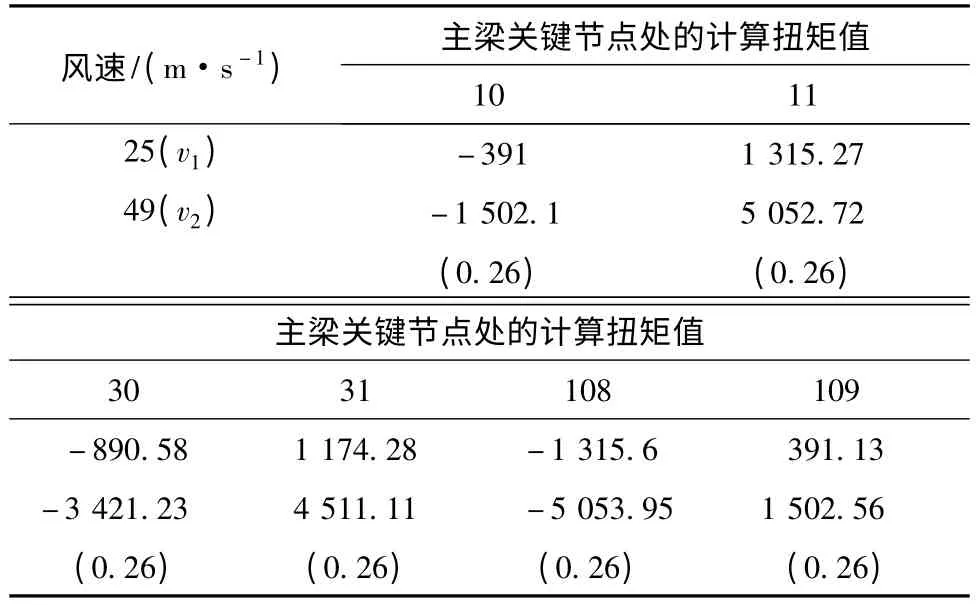
表2 主梁几个关键节点处计算扭矩值对比 (kN·m)

另外，考察对比3 个方向的弯矩值发现，最大弯矩为侧向弯矩My，这是因为静风三分力中静风阻力值最大，所以由静风阻力产生的侧向弯矩最大。图7 给出了两种风速下的主梁侧向弯矩对比，由图7可知，侧向弯矩在中跨跨中和塔梁处同时达到最大值，而且方向相反，在中跨1/4 跨附近与边跨中部的侧向弯矩达到最小值。两种计算风速下的侧向弯矩比值同样约为0.26。

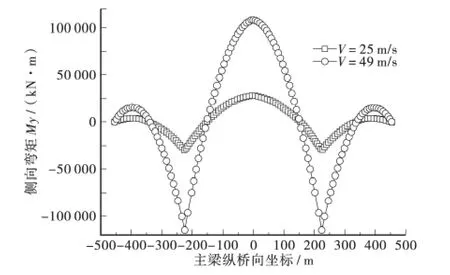
图7 主梁侧向弯矩对比

4 结论

本文通过对一座常规大跨斜拉桥进行了常遇风速与极端风速两种风速下的静风荷载响应分析，具体给出了常遇风速与极端风速下主梁横桥向位移、竖桥向位移、扭转角位移与横向剪力、竖向剪力、扭矩以及侧向弯矩沿桥跨的变化规律，得出了如下结论。

1)主梁三向静风位移沿桥跨变化规律并不一致，但横桥向位移、竖桥向位移和扭转角位移均是在中跨跨中达到最大值。这说明中跨跨中是此类斜拉桥的静风位移敏感截面，在施工以及运营阶段要尤为注意，尤其是极端风速(比如台风等大风期)时要做好位移控制措施。

2)主梁各个方向的静风内力响应沿桥跨变化规律迥异，其中只有横桥向剪力沿桥跨的变化规律为分跨线性关系，其余方向的静风内力均为非线性关系。横向剪力、竖向剪力、扭矩值均是在中跨跨中处达到最小值，塔梁处达到最大值，而侧向弯矩在中跨跨中与塔梁处同时达到最大值，但是两者方向相反。

3)对比分析常遇风速v=25 m/s 与极端风速v=49 m/s 两种风速条件下的静风响应发现，无论是静风位移还是静风内力，两种风速下的静风响应值比值在0.24 ～0.26 之间，这与两者风速的平方比值一致，这说明静风响应值与风速平方值具有一定的线性对应关系。

［1］JTG/T D60－01—2004，公路桥梁抗风设计规范［S］.

［2］程 进，肖汝诚，项海帆.大跨径斜拉桥非线性静风稳定性全过程分析［J］.中国公路学报，2000(3).

［3］李 俊，李小珍，程海根，等.宜宾长江大桥斜拉桥的抗风性能分析［J］.世界桥梁，2006(1).

［4］熊正元，颜全胜，李立军.大跨度斜拉桥的静风非线性稳定分析［J］.铁道标准设计，2004(9).

［5］杨上清，蒋玉川，曾 忠.大跨度斜拉桥非线性静风稳定性分析［J］.重庆交通大学学报(自然科学版)，2012(3).

［6］邹小江.斜拉桥风振响应时域分析及静风稳定性研究［D］.广州:华南理工大学，2003.

［7］康小方，方诗圣，张 利，等.静风荷载下的大跨度斜拉桥稳定性分析［J］.合肥工业大学学报(自然科学版)，2012(5).

［8］朱志虎.东海大桥主航道桥风致响应分析研究［D］.上海:同济大学，2007.

［9］张德铭，李德寅.斜拉索在风载、活载下的稳定性［J］.世界桥梁，2007(4).

［10］陈海兵，曾国良，陈明芳.混合梁斜拉桥钢混结合段的局部应力分析［J］.公路工程，2009(6).

［11］葛耀君，杨詠昕，赵 林，等.上海长江大桥主通航孔桥抗风稳定性能研究［J］.世界桥梁，2009(S1).

［12］黄 融，葛耀君.东海大桥主航道桥抗风性能及颤振控制研究［J］.世界桥梁，2004(B09).

［13］梁 柱，李 娜，张新越.深圳湾大桥实测风场参数与风致拉索振动响应分析［J］.公路，2009(7).

［14］杨 琪，李 乔.大跨度斜拉桥静力、动力和稳定智能仿真分析［J］.中南公路工程，2001(3).

［15］胡晓伦.大跨度斜拉桥颤抖振响应及静风稳定性分析［D］.上海:同济大学，2006.

［16］陈政清.桥梁风工程［M］.北京:人民交通出版社，2005.

［17］Simiu E，Scanlan R H.Wind Effects on Structures:Fundamentals and Applications to Design(3rd Edition)［M］.New York:John Wiley＆Sons Incorporation，1996.

［18］项海帆.现代桥梁抗风理论与实践［M］.北京:人民交通出版社，2005.