时间序列模型在山西省能源需求预测中的应用

张文丽，翟明娟，白 刚

（长治学院 数学系，山西 长治 046011）

经济增长与能源需求关系密切，两者相互影响，相互促进。由于山西省国民经济的增长以及居民消费结构升级等原因，对能源需求日益增加。科学合理准确地对山西能源需求量进行预测，对于正处在转型期的山西省可持续发展有着重要意义。

常用的预测方法主要有：回归分析法、弹性系数法、灰色预测法、时间序列方法[3]以及神经网络法等。文章以山西省历年能源消费量数据为基础（见表1），首先通过其趋势图形判断该时间序列的平稳性，若不平稳则需对其进行平稳化后才能建立模型；通过对平稳化后的时间序列数据的自相关系数和偏相关系数图形选择模型的类型；根据AIC准则和SC准则确定模型的阶数；利用最小二乘估计方法对模型的参数进行估计；通过对残差序列的白噪声检验[1]对模型进行检验；若模型通不过检验，则需建立新的模型，直至模型通过检验；利用检验后的模型对山西的能源需求量进行预测同时计算预测误差。

1 能源消费数据和时间序列的稳定性判断

从表2中可看到能源消费[2]随时间的变化呈明显的递增趋势，且呈指数变化。由表3知ADF=4.758026分别大于不同检验水平的三个临界值，是典型的非平稳时间序列。经过将能源消费数据取对数再取一阶差分后记为DLXt，且得到表4，由其折线图看出处理后的序列较平稳，对其进行ADF检验。从表5知处理后的序列ADF=-3.864908分别小于三个不同检验水平的临界值，所以处理后的序列平稳。

表1 山西省1991-2013年能源消费数据表（单位：万吨）

2 根据平稳化后的时间序列数据的自相关系数和偏相关系数图形选择模型

由表6知序列的自相关图和偏自相关图[4]都是拖尾的，通过观察表6知偏相关系数显著不为0的个数为1个，对应的滞后期为4，自相关系数显著不为0的个数为1个，对应的滞后期为4，故初步选择ARIMA（4,4）模型。

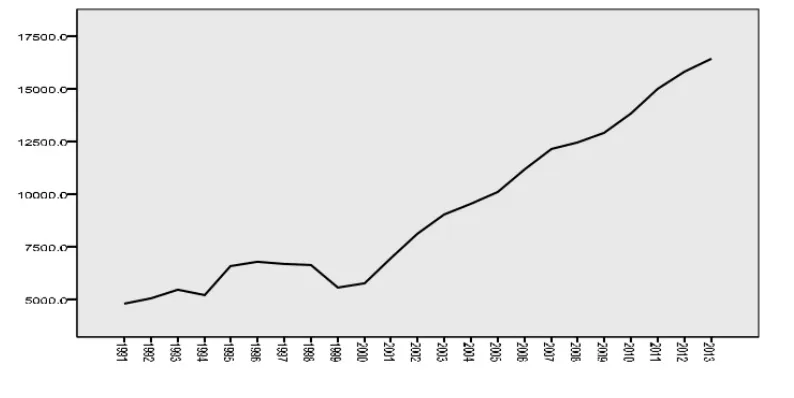
表2 山西省能源消费时间序列表

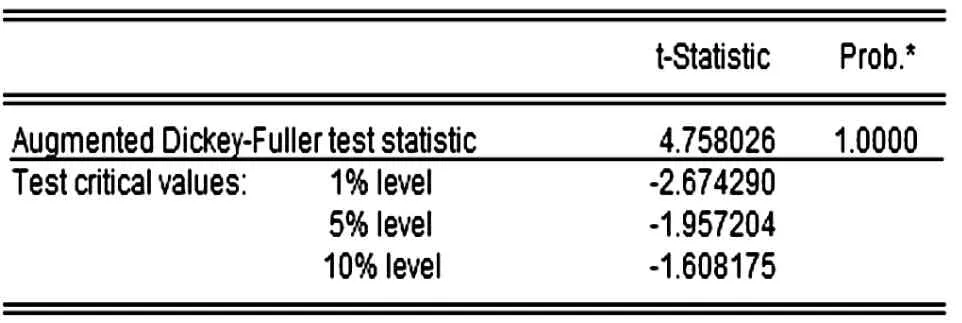
表3 山西省能源消费ADF检测表

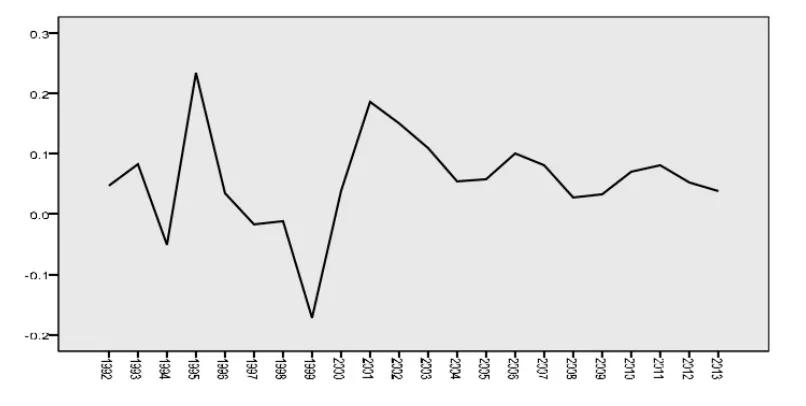
表4 山西省能源消费对数一阶差分时间序列表

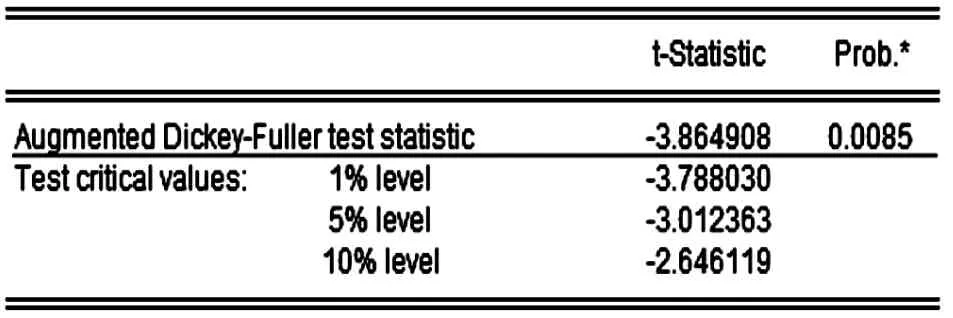
表5 山西省能源消费对数一阶差分ADF检查表

3 模型定阶、参数估计和模型检验，预测及误差的计算

通过计算比较不同的p,q值的AIC信息值[5]，根据解释变量的系数估计值是否显著，我们最终建立模型ARIMA(1，1)，由表7得其拟合方程为

利用ARIMA（1,1）模型对山西省2011-2018年能源消费进行预测，得到下列结果（见表8）。

表6 山西省能源消费对数一阶差分序列的自相关系数和偏相关系数表

表7 ARIMA（1,1）回归结果

表8 山西省2011-2018年能源消费预测值与实际值

从表中看到2011-2013年的预测值与实际值有些差距，但不大，说明建立的ARIMA(1,1)模型比较合理。通过对山西省能源消费进行预测，一方面揭示山西省能源消费总量数据之间的内在规律，另一方面对相关部门的决策提供一定的理论依据和参考，有利于能源的开发和利用，降低和避免能源浪费，具有一定的经济效益和社会效益，且能促进能源的可持续发展。

［1］朱艳科.广东省能源消费的ARIMA模型预测分析［J］.数学的实践与认识,2012,42(2):14-18.

［2］翟明娟.基于ARIMA模型的山西省能源消费的预测分析［J］.数学的实践与认识,2013,43(7):32-36.

［3］薛冬梅.ARIMA模型及其在时间序列分析中的应用［J］.吉林化工学院学报,2010,6(27):80-83.

［4］李良.EVIEWS软件在ARIMA模型中的应用研究［J］.安徽电子信息职业技术学院学报,2011,2(53):50-52.

［5］卢建明主编.《山西能源经济60年(1949-2009)》［Z］.中国统计出版社,2010,3.