基于MEMS传感器的姿态检测系统
王窕丽,孙玉国
(上海理工大学 光电信息与计算机工程学院,上海200093)
在车辆船舶的倾斜测量、机器人平衡姿态检测、飞行器惯性测量系统等许多方面都需要测量物体的姿态信息。随着军事科技的不断发展,姿态测量系统在无人机领域也得到了广泛应用[1]。姿态检测根据信息输入源的不同可分为两类:一类是通过外部信息源输入,通常采用摄像机、测距仪、超声波模块等外部传感设备;另一类是将加速度计、陀螺仪及电子罗盘等集成于目标物体内部,提供测量信息,称其为内部信息源。内部信息源传感器多数采用MEMS技术研制,具有抗冲击能力强、可靠性高、寿命长、成本低等优点[2]。
加速度计具有良好的静态特性,但是动态响应慢,不适合动态角度运动的跟踪测量;陀螺仪动态性能表现良好,但存在漂移误差,且随着时间累积而增大。若将加速度计和陀螺仪结合使用,将两者采集的数据进行融合,不仅可提高动态性能,且消除偏移,使得测量的角度与实际角度更加吻合。本文基于此理论,搭建了姿态检测系统,实时准确的检测出物体当前姿态,具有独立、简单、易用的特点,且有较好的实用性。
1 姿态检测原理
物体在地球上受到重力作用会产生加速度,加速度传感器可用来测量其值。当固定在目标对象上的物体姿态发生改变时,加速度传感器X,Y,Z 3个方向的敏感轴会相对于重力场发生改变,从而分别产生重力分量信号,如图1所示。

图1 三个姿态角示意图
当目标对象姿态处于变化中时,加速度传感器输出参数是重力加速度和物体本身加速度的矢量和,由于加速度传感器动态响应性能较差,同时在姿态改变的过程中会产生系统震动。因此,通过加速度传感器难以单独实现姿态检测。陀螺仪良好的动态特性提供了解决问题的方法,将陀螺仪提供的目标物体的瞬间动态角度变化与加速度传感器的测量值进行融合与矫正,通过引入一个缩放因子利用低通滤波器对加速度计、陀螺仪的噪声进行过滤,根据置信度低的加速度和磁场强度数据获取误差估计值,数据融合后对陀螺仪数据进行补偿,最大程度上降低噪声干扰,实现频域上的特性互补,提高测量精度和系统的动态性能。
2 整体结构框图
本系统由上位机和下位机两部分组成,下位机为硬件架构,主要由MEMS传感器、STC89C52单片机及无线模块等构成,负责数据的采集、处理和传输[3]。根据设计要求及资料分析,选取MEMS陀螺仪L3G4200D和加速度计ADXL345组成姿态模块[4],其精度高、抗振动能力强、能够满足实时准确获取物体运动过程中角速度、加速度的参数要求。无线模块作为信号传输模块,能够有效避免传输线路对物体运动的限制,同时经过跳频编程能有效的避免噪声干扰。
无线模块将接收的数据通过USB传送给上位机,从而实现整个系统间的通信。由于姿态测量的主要原理是对角速度的积分,并结合上一时刻的姿态进行姿态更新,处理量较大,因此将姿态更新部分交由上位机处理,并显示上位机对目标物体当前姿态的参数,绘制时域曲线图[5-6],系统整体结构框图如图2所示。
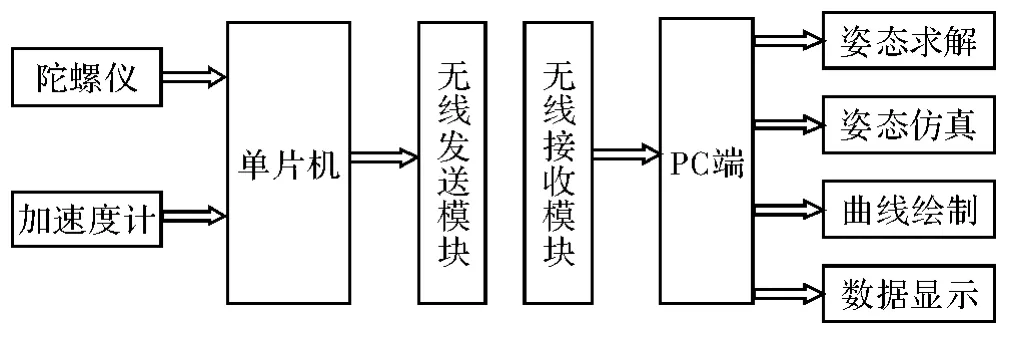
图2 系统结构示意图
3 物体姿态求解
3.1 姿态角求解算法
目标物体姿态求解是整个系统的关键构成部分。物体姿态角的描述需要建立基准坐标系,通常建立地理坐标系对目标物体进行定位,地球坐标系作为参考坐标系,由载体坐标系与地理坐标系的方位关系确定目标物体的姿态。目前,在姿态测量领域常用的姿态更新算法有欧拉角算法、方向余弦法、四元数法等。如果只讨论载体坐标和地理坐标的相对位置时,可通过等效旋转进行转换[7],转换的全部信息参数包含在四元数Q中,Q的定义如下
Q(q0,q1,q2,q3)=q0+q1i+q2j+q3k
其中,q0,q1,q2,q3为实数;i,j,k为虚部,且满足。
则其姿态变换的转换式如下

陀螺仪输出值是采样周期内角速度的增量,而不是实际的角速度值,直接通过角速度增量确定四元数,能有效避免系统误差在积分过程中增大而导致干扰信号增大。四元数法计算运动姿态是工程学中较实用的方法,求解线性微分方程只含有4个未知量,可满足实时性要求。但四元数旋转矢量算法本质上是一个类似列表的算法,在高频运动状态下姿态算法会产生较大的漂移误差。
3.2 滤波算法
由于传感器本身的固有特性,随着时间和温度的变化会产生不同程度的漂移。为获取物体的准确姿态数据,需要采用互补滤波算法进行数据融合[8]。通过将加速度的数据与陀螺仪的数据进行融合,能够有效地提高陀螺仪角速度的动态性能和加速度的静态精度,互补滤波过程如图3所示。
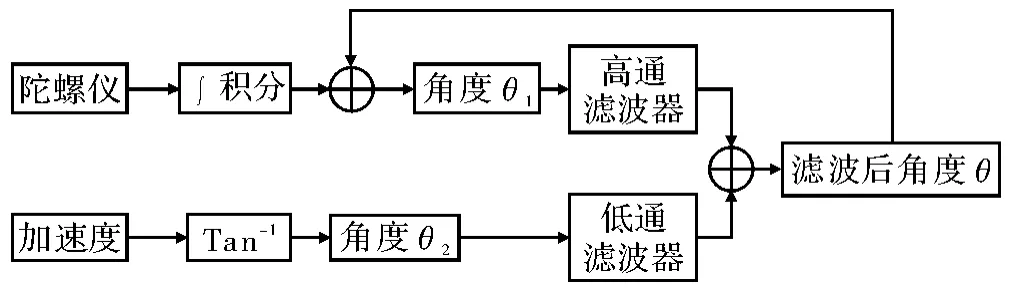
图3 互补滤波过程
离散化的一阶互补滤波方程为

式中,θn为n时刻滤波处理后获取的角度值;θ1n为陀螺仪采集处理后的角度值;θ2n为角速度计数据处理后获得的角度值;dt为采样周期;K为滤波系数;τ为时间常数,其与滤波截止频率有关。互补滤波效果主要取决于滤波系数K,K较小时,截止频率低,测量结果主要依赖于陀螺仪测得数据,不利于剔除随时间而累积的漂移的影响,K较大时,截止频率高,易受低频、幅值较大的运动加速度的影响。
针对互补滤波的不足,本文采用了基于四元数的互补滤波算法。在加速度计输出结果只受到重力加速度而无其他线性加速度干扰的情况下,将地理坐标系中的重力和磁场强度换算到载体坐标系中,分别对角速度向量和磁场向量进行计算,获取方向向量误差,将方向向量误差转换为四元数形式,通过方向向量误差对角速度向量不断修正,获取更新后的四元数信息,正交单位化后转换为姿态角信息,循环重复这一过程能够持续对运动姿态进行更新。基于四元数的互补滤波姿态融合算法能够有效的避免重力加速度的线性干扰,简化系统的计算过程,同时对四元素换算过程中的不可转换误差也起到了良好的抑制作用,降低系统滤波器实现成本,提高系统的实时性和精度指标要求。
4 系统软件设计流程
该系统下位机是基于单片机的传感器数据采集和发送,上位机接收并匹配使其重新组合成准确的信息,通过基于四元数的互补滤波算法进行数据耦合得到目标物体的姿态信息。下位机主程序流程图如图4所示。
在无线模块传输过程中,噪声和其他无线通信设备容易对其产生一定频率和脉冲干扰,为提高系统抗干扰能力,本文采用跳频处理方法对无线模块进行改进[9]。跳频实现的频段和信道可根据用户实际需求确定,本文中频段选取2.423 GHz和2.445 GHz,系统跳频实现发送和接收数据的流程图如图5所示。

图4 下位机主程序流程图
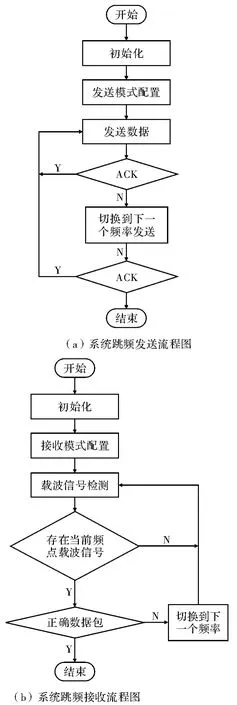
图5 系统跳频发送和接收流程图
5 系统调试及分析
为使传感器输出的结果更准确,在数据采集前,通过软件编程对器件的零漂进行了处理,最大程度上减小零漂和其他误差对姿态信息的干扰。系统调试主要是物体处于静止和运动时的反复测试,当静态角为0°时,对目标物体姿态进行检测,图6是测试结果。

图6 静态角度为0°时测量角度及互补滤波结果
将传感器模块放置于JZJ-1型准直仪支架上,调整支架底座上的水泡使其处于水平状态。以准直仪支架的角度读数为真值来分析传感器模块实测值的误差。如表1所示,大部分情况下测量平均值与真值之间的误差保持在0.2°以内。
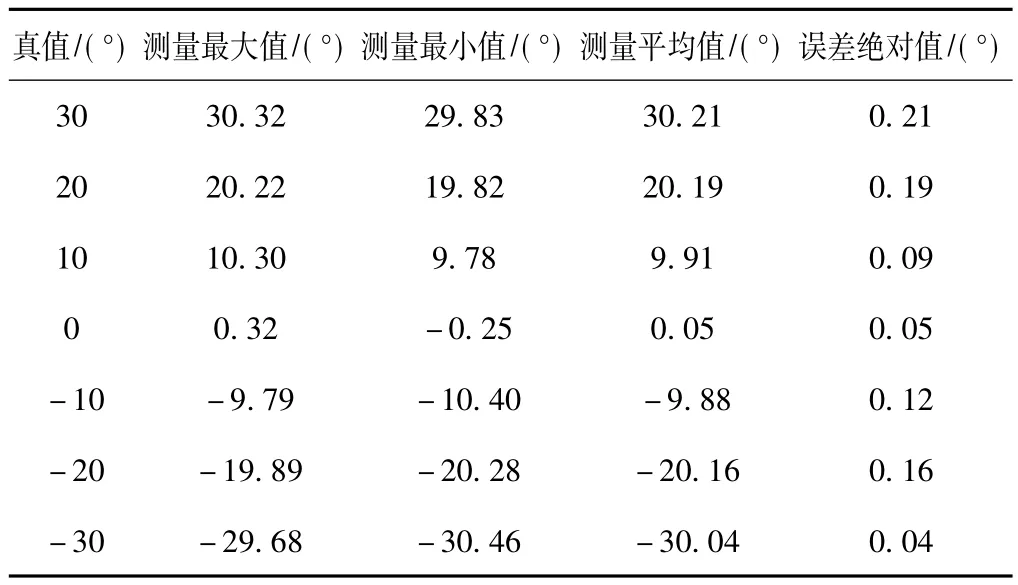
表1 静态滤波后角度值及其误差
当目标物体处于运动时,对其进行检测,加速度计、陀螺仪及经过滤波后的角度和加速度数据曲线如图7所示。
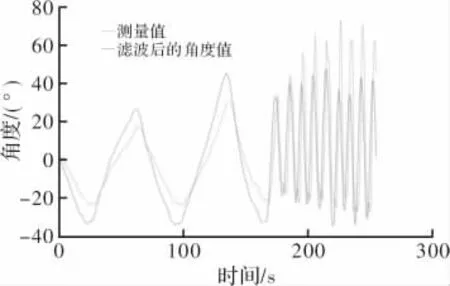
图7 动态角度测量及互补滤波结果
由于传感器置于准直仪支架上,本系统针对俯仰角的测量,在相应轴上的线性加速度对于测量结果误差并不明显,在实际应用中,会受到运动加速度影响而产生较大误差。仿真结果表明,滤波后数据曲线更为平滑,滤波效果良好。
6 结束语
本文在已有运动姿态检测系统资料的基础上,结合姿态解算的基本原理,设计并实现了一款精度较高、可靠性好的物体运动姿态测量系统,分为上、下位机两部分。通过无线模块实现实时高效的数据传输,互补滤波算法有效结合陀螺仪的动态性能和加速度计的静态性能,实现频域上的互补,提高系统的测量精度。通过四元数方法求解姿态矩阵,在准确地计算运动姿态的基础上,降低了系统运算量,减少了对于时间和资源的消耗,同时对系统实时性也起到了提升的作用。该系统简单易用,具有良好的应用价值。
[1] 赵鹏,沈庭芝,单宝堂.基于MEMS的微型无人机姿态仪的设计[J].火力与指挥控制,2009(6):164-167.
[2] 曹晓棠,石云波,周兆英,等.基于MEMS的微型飞行器姿态测量系统[J].传感器与微系统,2013(2):122-123.
[3] 苏菲,尚德重,汪建波等.基于陀螺仪和加速度计的帆船运动姿态测量[J].太赫兹科学与电子信息学报,2014,12(2):183-189.
[4]Ma Chao,Zheng Yongjun,Tan Yu,et al.Design of two-axis attitude control system based on MEMS sensors[J].Transactions of the Chinese Society of Agricultural Engineering,2015,31(Z1):28-37.
[5] 赵翔,杜普选,李虎,等.基于MEMS加速度计和陀螺仪的姿态检测系统[J].铁路计算机应用,2012,21(3):15-18.
[6] 刘娜娜.基于MEMS传感器的姿态检测系统设计[D].哈尔滨:哈尔滨工业大学,2011.
[7] 周亢,闫建国,屈耀红.全角度姿态角解算方法研究与仿真[J].系统仿真学报,2009,21(6):1697-1700.
[8] 边群星,陈锟,陈郑洲.基于互补滤波器的两轮平衡车姿态角度测量[J].电子设计工程,2014,22(18):55-58.
[9] 任强,周升良,孙玉国.基于MEMS的角位置无线随动系统设计[J].传感器与微系统,2013,32(9):122-124.

