一种基于改进SURF特征描述子的快速算法

时培弘，董淑福，单 勇

(空军工程大学 信息与导航学院，陕西 西安710077)

SIFT［1］算法和SURF算法作为局部特征提取算法被广泛应用，为模式识别乃至深度学习［2］奠定了基础。近年来各国学者提出许多局部特征描述子，如局部二值描述子ORB［3］、BRIEF［4］、FREAK［5］、Brisk［6］等，但都不同程度地对尺度变化和角度旋转敏感，鲁棒性不强。SIFT算法是目前为止最为稳定的特征点提取算法，从提出至今不断被优化，其中SURF算法是对SIFT算法的优化。SURF算法引入了积分图像及盒子滤波器等方法［7］，避免采用SIFT中的降采样［8］构造图像金子塔，而是令图像尺寸不变，滤波器尺寸相应改变［9］来滤波原图像(这一过程可以并行处理［8］)，上述一系列操作简化了Hessian矩阵行列式和哈尔小波响应的计算［9］，将算法的运算速度提至SIFT算法的3～5倍［10］，在保证运算速度的同时兼顾了稳定性［11］。与SIFT算法类似［12］，为保证旋转不变性，SURF特征描述子依赖于关键点的主方向，在计算出主方向后，还需以主方向为基准计算出邻域内哈尔小波响应。其中计算主方向和计算哈尔小波中包含大量扫描计算［13］与浮点运算。

本文利用各向同性的向量重新定义SURF特征描述子，在保证旋转不变性的基础上节省了确定主方向和旋转哈尔小波响应的运算时间，并且新定义的描述子在计算过程中利用了积分图像，加快了计算速度。

1 SURF算法

SURF算法主要分为3部分［14］:(1)特征点提取。(2)特征描述子的生成。(3)利用描述子匹配特征点。以下主要介绍描述子生成，也是本文所改进的部分。

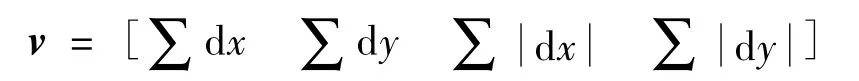
这样最终形成4×4×4=64维描述子。

上述操作中，为得到哈尔小波响应，需要将旋转前的点进行二维旋转［8］，令旋转前的坐标为(l，k)，旋转后的坐标为(x，y)，其满足

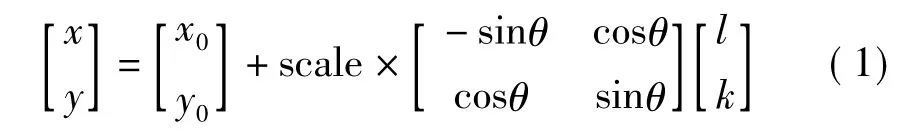
得到(x，y)后，求取水平与垂直方向的dx和dy，高斯加权后按式(2)得到dx'和dy'

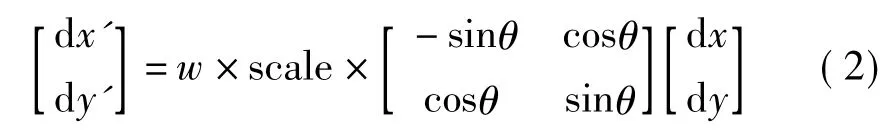
2 对SURF算法的改进

本文利用各向同性数学量重新构造特征描述子，使描述子具有旋转不变性，使算法免于计算特征点主方向所用到的扇形扫描和哈尔小波旋转所产生的浮点运算。同时新的描述子利用了积分图像，加快了计算速度。

与原算法类似，以特征点为中心，构造16s×16s方形区域，以同心圆划分方形区域，如图1所示，形成8个子区域，每个子区域计算区域内点的像素值与特征点像素值之差dr和，以特征点为中心，3.5σ高斯加权后，形成子区域的前两维

然后分别依据特征点尺度计算各个子区域内的每一个点一阶拉普拉斯算子之和与LoG算子响应之和，2.5σ高斯加权后形成子区4维向量

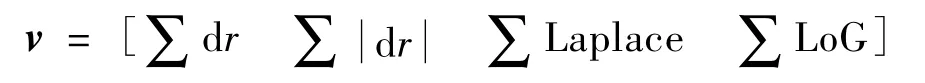
这样最后形成8×4=32维描述子。由于径向差分、Laplace算子和LoG算子都具有各向同性，最终构造的描述子满足旋转不变性。

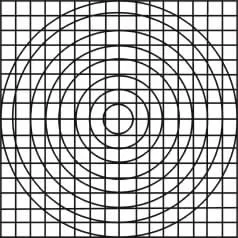
图1 本文算法区域划分

图2 3×3拉普拉斯模

图3 5×5 LoG算子模板

上述运算中，求取一阶拉普拉斯算子和LoG算子响应时利用了积分图像。为利用积分图像，算子可作分解处理。

其中，分解后的纯量阵可直接利用积分图像计算。最终形成的描述子满足旋转不变性。

3 实验结果分析

实验主要测试当图像发生尺度、旋转、模糊时修正后与修正前算法匹配的正确率和匹配速度。如图4～图6，每组第一张为原图，后4张为在原图基础上尺度、旋转、模糊变化。实验所用素材为300×400的彩色图像，测试软件为Matlab 2013b，硬件平台CPU为i5－4200U 1.60 GHz的个人电脑。

图4 尺度变化的图像

图5 旋转变化的图像

图6 模糊变化的图像

表1 本文算法与原SURF算法性能比较

对于尺度变化而言，随着尺度变大，原SURF算法和本文算法正确匹配率均降低，并且识别率总小于原SURF算法。原因是尺度变大时，本文算法中描述子所用到的一阶拉普拉斯算子和LoG算子尺寸随尺度增长剧烈，导致过多信息被计算到描述子中，令误差变大，改善方法是选取合适尺寸的各向同性数学。

对于旋转变化来说，本文算法保持了良好的正确率，如图7所示。由于本文算法匹配所用到的描述子具有各向同性，对图像的旋转不敏感，所以对于各种角度算法均能保持较高的匹配率。

图7 旋转时本文算法匹配效果示例

对于模糊变化，随着模糊程度增加，本文算法与SURF算法正确匹配率都随之下降。由于模糊程度增加，本文描述子由灰度信息构成，不能体现关键点的方向性，且维度是SURF算法的1/2，信息过于单薄，不能较好地反应模糊后图像与原图像的匹配关系，造成匹配率低于SURF算法，如图8所示。

从运行速度上来说，本文算法的表现优于SURF算法。原因如下:(1)各向同性描述子的引入省去了计算主方向所用到的扇形滑动窗口扫描和哈尔小波旋转所产生的浮点运算。(2)描述子中一阶拉普拉斯算子和LoG算子的计算利用了积分图像。(3)描述子的维度小于SURF描述子。

图8 模糊时本文算法匹配效果示例

4 结束语

本文算法与SURF算法最大区别在于关键点周围区域的划分方式和描述子所用到的信息。SURF算法将区域划分为4×4=16个子块，每一个子块在尺寸上大小一致，位置紧凑，将16个子块的每一子块中心点视作区域的“骨架”，以主方向为基准分别形成丰富的64维信息，由于以方向为区别，SURF描述子具有较高的辨识度。本文算法是以同心圆划分区域，每个圆环域作为整个区域的“骨架”，并且随着圆环距离特征点越来越远，圆环增大，点数增多，与其他子块不够紧凑，虽用高斯加权，但子块所形成的向量独特性减弱。但也正是因为划分方法不同，使本文算法在误差范围内得以加快计算速度。使新算法所消耗的时间大幅减少。重新构造的特征描述子利用了积分图像，因而可以进一步加快计算速度。本文算法需改进的地方较多，其中最重要的是在精细划分区域的基础上引入更多更优秀的各向同性数学量，使描述子信息更丰富，辨识度更高。

［1］Lowe David－G.Distinctive image feature transfrom scaleinvariant keypoints［J］.International Journal of Computer Vision，2004，60(2):91－110.

［2］ 杜骞.深度学习在图像语义分类中的应用［D］.武汉:华中师范大学，2014.

［3］ 章杰.基于ORB特征和粒子滤波的目标跟踪算法研究［D］.吉林:吉林大学，2014.

［4］Calonder M.BRIEF:binary robustindpendnt elementary features［C］.ToYonto:ECCV，2010:778－792.

［7］Bay H，Ess A，Tuytelaars T.SURF:speeded up robust features［J］.Computer Vision＆Image Understanding，2008，110(3):346－359.

［8］ 李云霞，曾毅，钟瑞艳，等.基于SIFT特征匹配的图像拼接算法［J］.计算机技术与发展，2009，19(1):43－45.

［9］ 王永明，王贵锦.图像局部不变特征与描述［M］.北京:国防工业出版社，2010.

［10］吴锐航.基于SIFT特征的图像检索技术［D］.厦门:厦门大学，2007.

［11］刘少鹏，郎跃东，丁祝顺.改进SURF算法及其在目标跟踪中的应用［J］.传感器与微系统，2012，31(12):148－152.

［12］崔振兴，曾威，杨明强，等.一种改进的SURF快速匹配算法［J］.江苏师范大学学报，2014，32(3):41－46.

［13］徐晓鹏.基于改进SIFT算法的目标识别研究［D］.南京:南京理工大学，2011.

［14］石雅笋.改进的SURF图像配准算法研究［D］.成都:电子科技大学，2008.

［15］林怡，应旻，杨业，等.改进的SURF算法在彩色车载影像匹配中的应用［J］.同济大学学报:自然科学版，2014，42(4):624－629.