动力定位系统舵桨组合推力分配研究

袁伟，俞孟蕻，朱艳

（江苏科技大学电子信息学院，江苏镇江212003）

动力定位系统舵桨组合推力分配研究

袁伟，俞孟蕻，朱艳

（江苏科技大学电子信息学院，江苏镇江212003）

针对船舶动力定位系统推力分配中舵桨组合的推力建模及优化分配问题，将舵桨组合的非凸推力区域转化成4个凸区域，采用切换控制理论把非线性最优化问题转换为线性最优化问题。将舵、桨组合起来进行推力建模，以最小推力、舵角变化和推力误差为优化目标，对推进器的推力变化率、舵角变化率、推力误差范围和推力大小作了约束，采用多边形的方法把推力范围约束转化为线性不等式约束，基于总功率与总推力误差在不同推力区域设计了切换逻辑，实现了在不同的推力分配器中的切换。实船试验结果表明舵桨组合推力模型及推力分配策略是切实可行的，满足了推力分配的要求，在配备舵的动力定位船上具有良好的应用前景。

动力定位；推力分配；舵桨组合；推力模型；非线性优化；切换控制

0 引言

21世纪是海洋经济时代，随着海洋产业的高速兴起，动力定位系统对于海洋钻井平台、起重铺管船、布缆船、平台供应船、大型耙吸挖泥船等海洋工程船舶/平台来说，已成为其海上作业特别是深海作业时必不可少的支持系统，是我国加快海洋资源开发不可缺少的海洋工程装备。

推力分配策略是动力定位控制系统重要组成部分，其性能的好坏不仅会影响系统的定位精度，还会影响到推进系统的能耗、排放和磨损。推进系统作为动力定位系统的执行机构，一般包括全回转推进器、可调螺距螺旋桨、舵、导管推进器、喷水推进器等。尽管全回转推进器是动力定位系统船舶最理想的推进器，但仍有很多动力定位船舶采用传统的推进方式，而襟翼舵、鱼尾舵等高升力舵在定位时它的最大升力可以达到主推系柱推力的40%-50%，因此在动力定位系统中如何更高效地使用舵可以减少全船的功率和能耗；另外，在一些耙吸挖泥船等非全电力推进工程船中，推进器为双可调桨+双舵和艏侧推，舵采用襟高升力舵，而不使用艉侧推，这样不仅可以提高该船的横向力，又可以优化船体的布置。然而，舵桨组合的推力与螺旋桨系柱推力、舵角、响应时间和航速相关，建立精确推力模型比较困难，其推力区域又是一个非凸区域，这样舵桨组合船动力定位推力分配成了一个非线性优化问题，增加了推力分配优化的困难。

目前大多数动力定位推力分配优化策略主要是研究多全回转推进器的优化策略，而针对舵桨组合的推力分配优化策略较少。文献[1-6]对推力分配优化问题进行了综述，把推力分配优化问题主要分为线性约束分配和非线性约束分配两类，采用的优化方法主要有两类：序列二次规划、最小二乘、拉格朗日，遗传算法、模拟退火、粒子群等智能优化方法。文献[7]提出了舵桨组合的推力分配优化方法，但是该方法中同一时刻只能使用一个舵不能同时使用二个舵。文献[8]中采用mp-QP离线优化的方法对舵桨组合推力分配进行优化，但是该方法没有考虑推进器的机械特性，也没有考虑推力变化约束，不能在线修改推进器的相关参数，限制了该方法在不同船舶动力定位系统中的在线应用。

本文以耙吸挖泥船动力定位系统推力分配为研究对象，首先对襟翼舵和主推组合起来建模，把舵桨组合推力建模成与主推系柱推力和舵角的扩展推力模型；然后提出了一种以能耗最优、最小舵变化频率和最小推力误差为优化目的，针对推进器的机械和操作约束，对主推和侧推的最大最小推力、推力变化率和舵角变化率限制，采用切换控制理论把该船的推力分配从非线性优化转化为线性二次规划求解出每个推进器的控制指令。

1 推力分配概述

动力定位系统由滤波器、控制器和推力分配组成；滤波器是为了剔除由一阶波浪力引起的高频运动，经滤波器估计的位置和艏向信息传动给控制器，减少推进器的磨损和能耗；控制器根据位置和艏向的设定值与当前滤波器估计值之差，计算出需要恢复到设定位置和艏向的力和力矩；推力分配根据控制器计算出的力和力矩，优化计算出船舶上各个推进器的扩展推力，然后根据推进器推力特性计算得到各个推进器的控制指令，船舶上的推进器控制系统根据推力分配的指令执行，使船舶恢复到设定的位置和艏向。

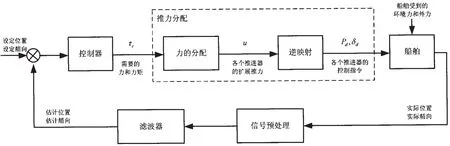
图1 动力定位系统控制框图Fig.1 Block diagram of dynamic position system

推力分配是一个动态的非线性优化问题，通常是多约束、多目标的，它是在约束条件下从期望控制量到各个推进器控制指令的非线性映射过程。对于一般海上水面作业船舶来说，动力定位系统考虑纵荡、横荡和艏摇3个自由度的水面运动，相对应推进器需产生克服外界环境和干扰力之和的力和力矩，即作为推力分配输入值。而一般情况下具有动力定位功能的船舶配有多数量和多种类的推进器，控制量u∈Rr，r＞3，因此该船是可控的且是过驱动的，推力分配就是要在这个冗余的推进器系统中寻优，得到各个推进器的控制指令。

2 推力模型

目前大多数文献中关于舵的升力和阻力模型都是描述在高航速下的推力模型，舵的升力和阻力模型与舵的升力系数、阻力系数和来流速度相关，然而动力定位系统工作时，船舶的航速一般在1 kn以下，这时舵的来流速度很难估算，不能按照典型计算舵的升力和阻力的公式（1）进行计算：

舵桨组合推力模型采用扩展推力的概念，它的纵向和横向推力为，建模成在不同舵角下与主推进器推力的百分比关系，通过模型试验或Fluent计算得到船舶在低航速下推力与舵的来流速度的关系，得到在不同舵角下和螺距下舵桨组合的推力[7-9]。如图2所示，舵桨组合的横向力是桨的最大系柱推力的50%左右，舵桨组合中只有推进器为正螺距时，舵才能产生升力和阻力，因此舵桨组合的推力区域是一个非凸区域。为正螺距时，推力区域是一个关于X轴对称的扇形；为负螺距时，推力区域是一条沿X轴负方向的直线。

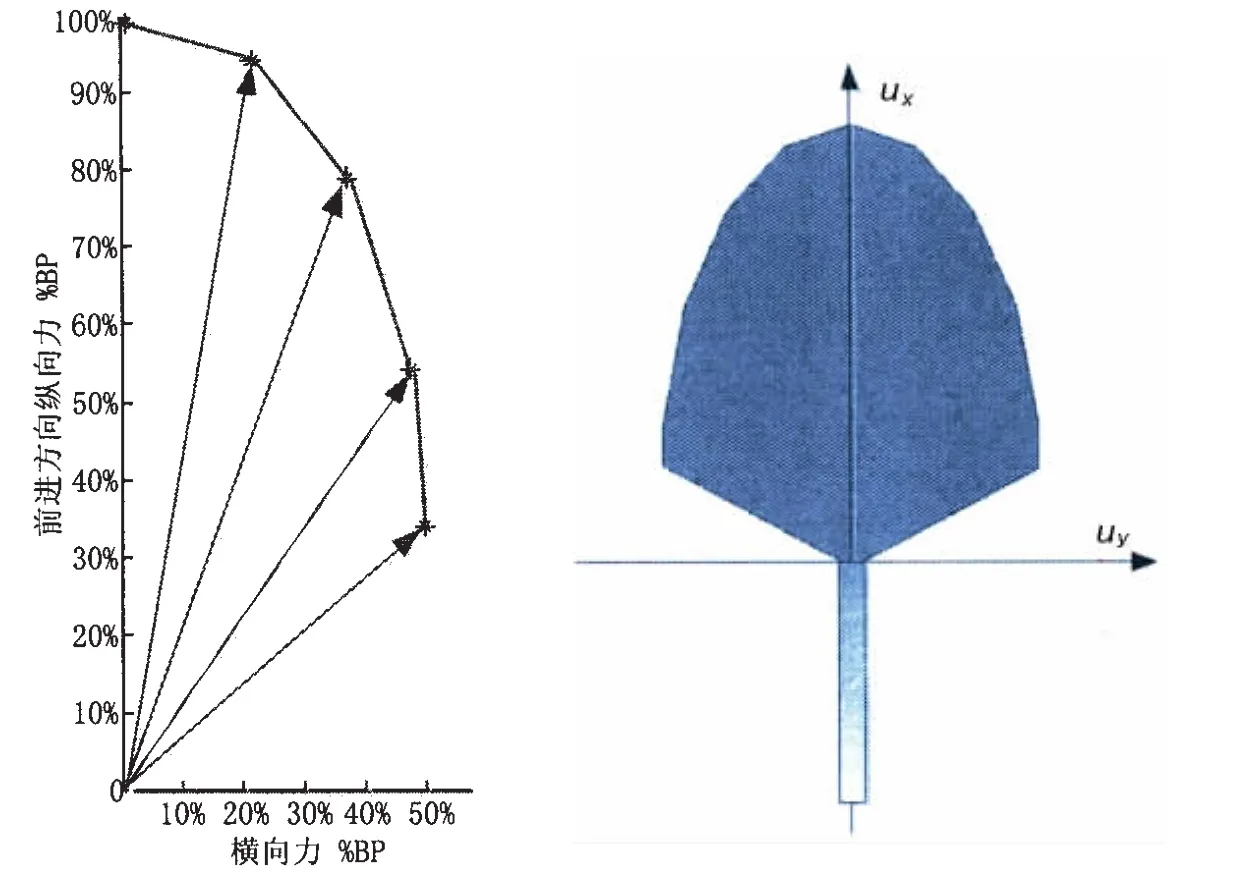
图2 舵桨组合推力区域图Fig.2 Attainable thrust region for propeller with rudder

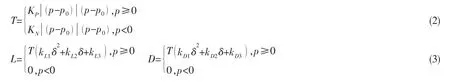
其中：T为调距桨的推力，KP为正螺距时的推力系数，KN为负螺距时的推力系数，L为舵产生的升力，D为舵产生的阻力，KLi为不同舵角下升力与调距桨推力的系数，KDi为不同舵角下阻力与调距桨推力的系数，KL和KD根据图2曲线得到，p为调距桨的螺距，p0为调距桨推力为零时的螺距，δ为舵角，舵桨组合的推力模型为：

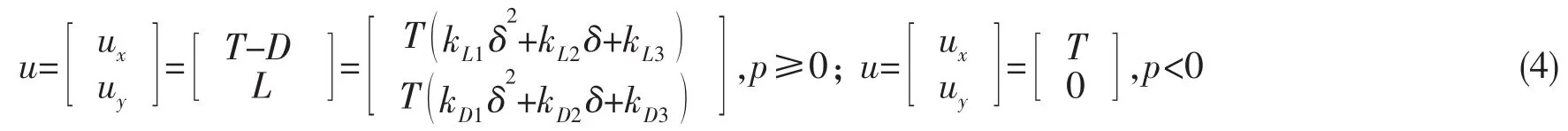
侧推的推力模型为：

如图3所示的推进器坐标系中，设船舶的重心坐标为（xCoG，yCoG），推进器的坐标为（x，y），T1、T2分别为左、右调距桨的推力，T3为艏侧推的推力，u1、u2、u3分别为左舵桨组合、右舵桨组合和艏侧推的扩展推力。推力分配模型为：

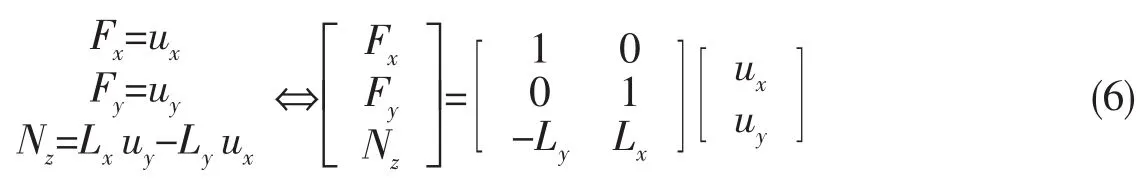
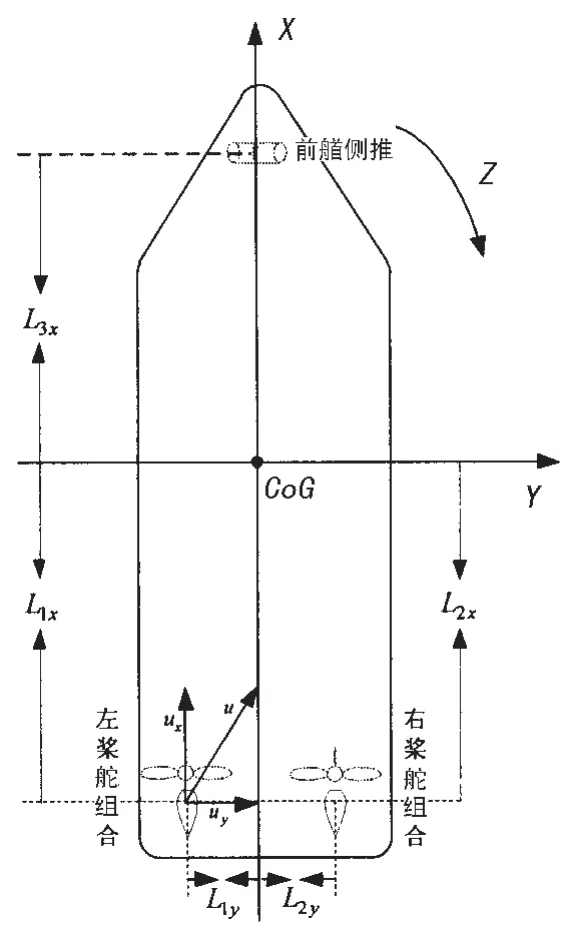
图3 耙吸挖泥船推进器布置图Fig.3 Actuator configuration of suction hopper dredger

根据图3，可得到该耙吸挖泥船动力定位系统推力分配模型为：

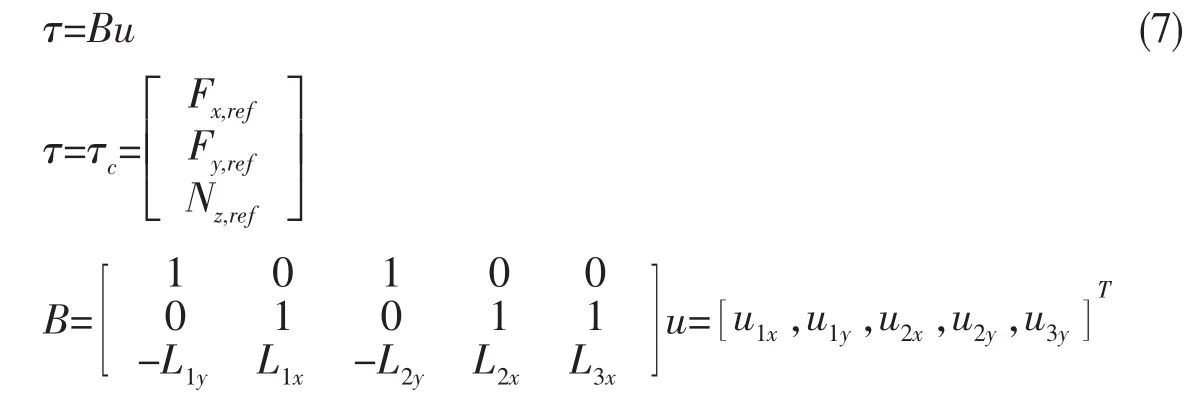
3 推力分配优化

以能耗最优、最小舵变化频率和最小推力误差为推力分配优化目标；考虑推进器的静态和动态约束，根据推进器的机械特性进行约束，包括对推力变化率和舵角变化率限制。推力分配的目标函数为：

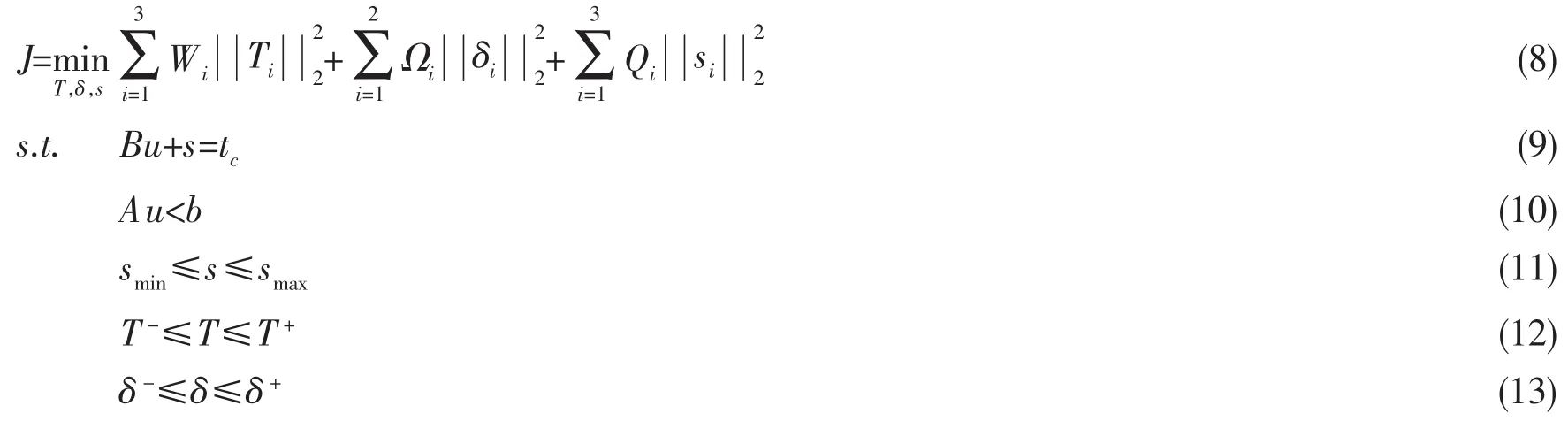
目标函数中第一项表示各个推进器的能耗，权值矩阵W＞0，其取值表示各推进器推力和总能耗的关系；第二项表示舵的使用情况，权值矩阵Ω＞0，其取值表示舵的变化频率；第三项为推力分配的推力误差，权值矩阵Q＞0，矩阵中值分别表示动力定位中纵向、横向和艏摇哪个方向最优。

约束条件中（9）式为等式约束，包括纵向、横向和艏摇三个方向的推力等式，引入松弛变量s，使得优化问题在允许误差范围内可解。（10）式为描述图2中纵向推力为正的推力区域的线性不等式约束，采用多边形的方法把该推力范围约束转化为线性不等式约束[9]。（11）式为推力误差的范围，也就是松弛变量s的范围。

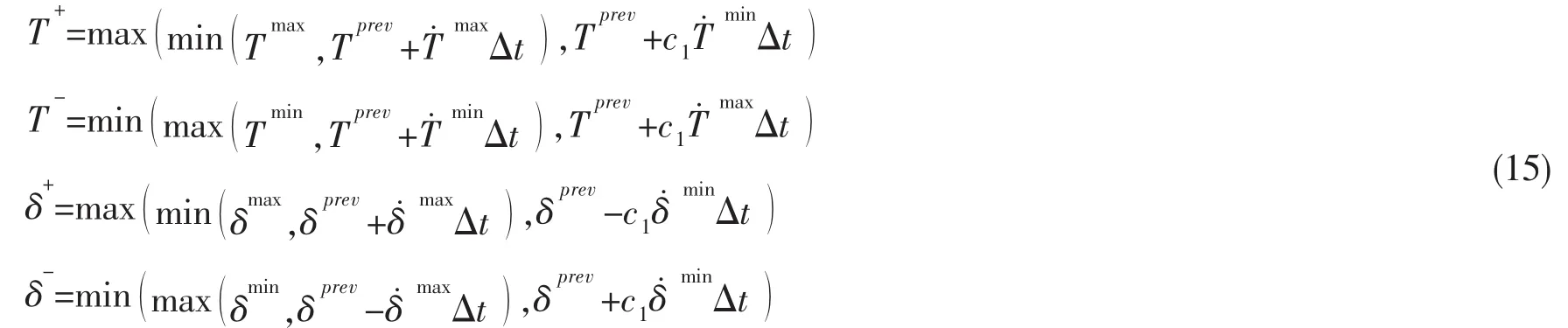
由于主推进器和舵机的机械特性限制，主推进器的螺距调节时间较长，舵机转速不能过快，必须对主推进器的推力变化和舵角变化加以限制。本文采用文献[10]中的方法对推力变化和舵角变化采用了动态约束，（12）式和（13）式分别为调距桨推力的动态约束与舵角的动态约束，（15）式为每个采样时刻具体的推力大小和舵角范围。

如图2所示的推力区域为非凸区域，根据文献[1]非凸区域的推力分配很难计算。在文献[5]中，把舵桨组合推力的非凸区域转化为两个凸区域后，采用的离线优化方法进行凸优化。本文采用类似文献[5]中的方法把两个舵桨组合推力区域分成四种组合，即（1）u1x≥0，u2x≥0、（2）u1x≥0，u2x＜0、（3）u1x＜0，u2x≥0、（4）u1x＜0，u2x＜0，但本文采用在线优化的方法，这样可以实时地设置推进器的功率、是否使用舵、选择推力分配模式等；采用切换控制理论解决舵桨组合推力分配中在4个子推力区域中切换以及不同推力模式的切换，实现能耗最优。推力分配中根据计算得到的推力T、松弛变量s和操作员设定的推力分配模式在不同的子推力区域中进行切换。

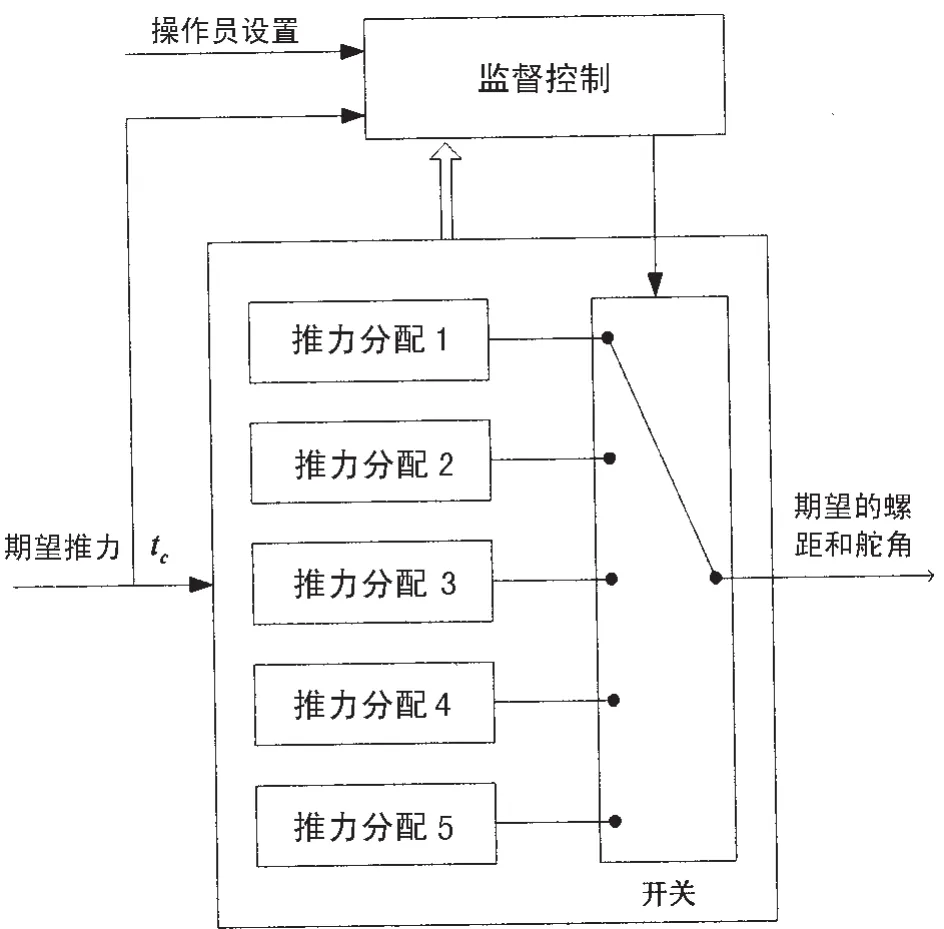
图4 切换控制结构图Fig.4 Block diagram of internal structure of switched thrust allocation system

为了实现推进器在不同推力区域中平稳的切换，推力分配之间的切换逻辑的选择尤为重要。为了避免频繁切换带来的抖动的影响，引入了滞后切换和停留时间的思想。文献[10]中给出了一种切换逻辑，它是基于各个推力区域的最小代价函数建立的。本文为了防止切换到比当前推力区域能耗还高的推力区域引入了功率滞后，为了防止切换到能耗较优但是推力误差较大的推力区域引入了总推力误差滞后。

根据推力与功率的关系计算每一个区域的总功率与总推力误差，基于最小能耗和推力误差原则找出最优的推力区域Is。

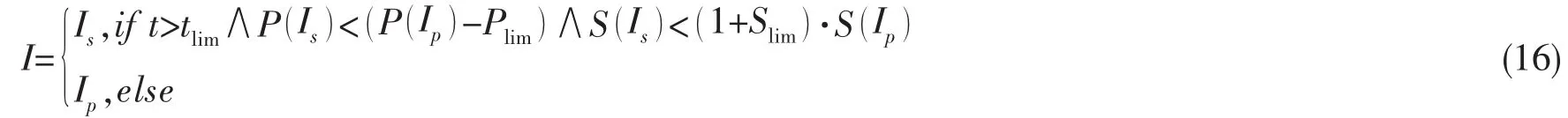
其中：t是从前一次切换开始的时间，tlim是滞后时间最小值，P（·）、S（·）分别是特定区域的总功率与总推力误差，Plim、Slim分别是总功率与总推力误差的极限值，Plim的单位是N，Slim的单位是%，Slim=10%在本推力分配中系统也能较好地工作，Ip是前一个推力区域，Is为最优的推力区域。考虑到调距桨的螺距调节特性，经过多次仿真和试验，滞后时间为tlim=20 s，误差极限为Slim=10%。

通过上述方法舵桨组合的优化转化为二次规划问题，采用开源的OOQP求解器对上述推力分配问题进行求解。在动力定位系统使用过程中，使用该在线优化求解器，可以动态设置推进器功率使用范围与处理推进器故障，可通过动态的设置约束值或者权值矩阵实现，例如：当不使用某推进器时可设置，舵角使用范围可通过设置

4 试验结果

为了验证上述推力分配策略的有效性，在某耙吸挖泥船上对该推力分配策略进行了实船验证，该船及推进器的参数如表1所示，实验过程中控制器采用PID控制器，滤波器采用扩展Kalman滤波器。控制计算机采用研华610工控机，配置为：CPU E7400，内存2G，控制系统采样时间为2 s。由于耙吸挖泥船没有艉侧推，横荡方向移船时必须要使用舵，因此特定设计了保持当前艏向向右平移的试验，试验内容为保持当前艏向，向右平移15 m，试验海况大约为：风速8 m/s，风向相对于船艏向270°。图5-7给出了挖泥船定位时的位置和艏向误差曲线，图8-10给出了推力分配的输入与输出的误差，图11-13给出了各个推进器经推力分配优化后的控制指令。

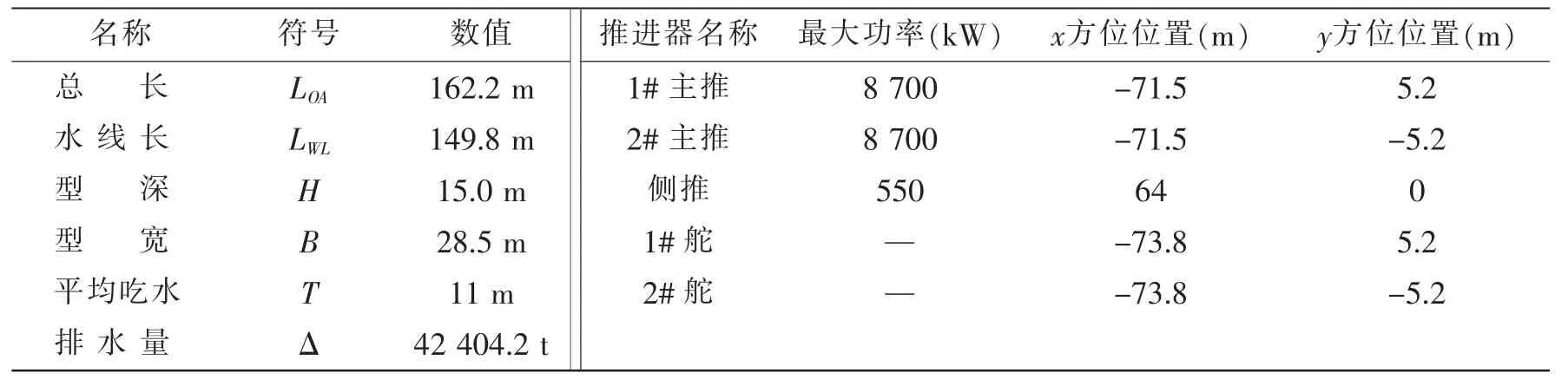
表1 耙吸挖泥船主尺度和推进器参数Tab.1 Main parameters and thruster parameters of suction hopper dredger

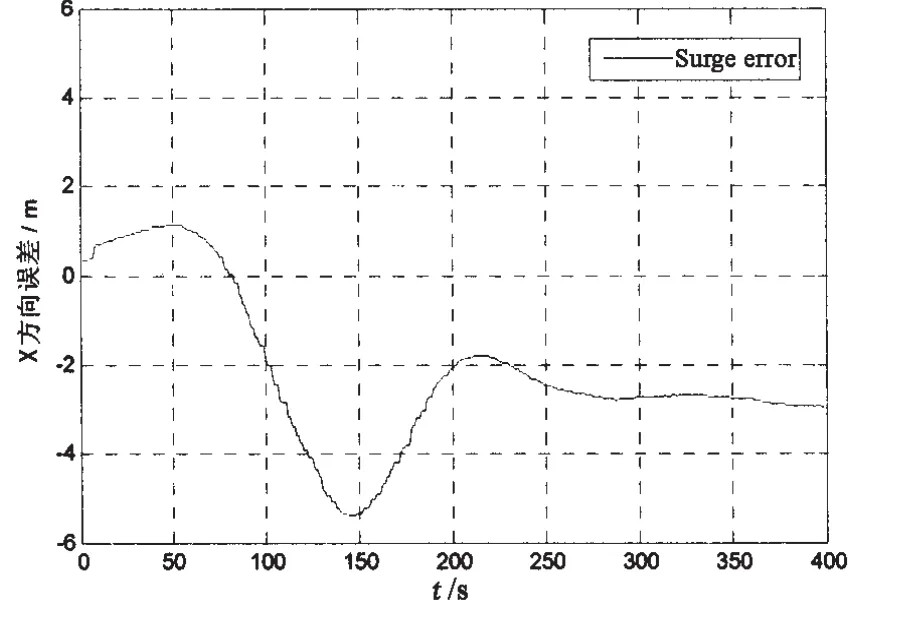
图5 纵荡方向位置误差Fig.5 Position errors in surge

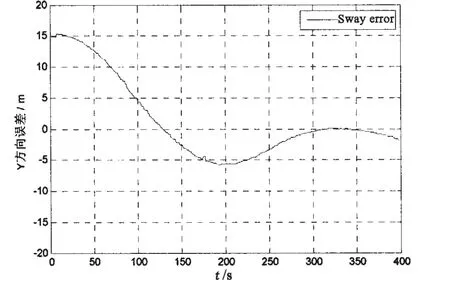
图6 横荡方向位置误差Fig.6 Position errors in sway

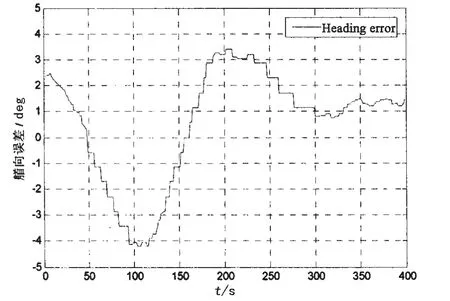
图7 艏摇方向误差Fig.7 Position errors in yaw

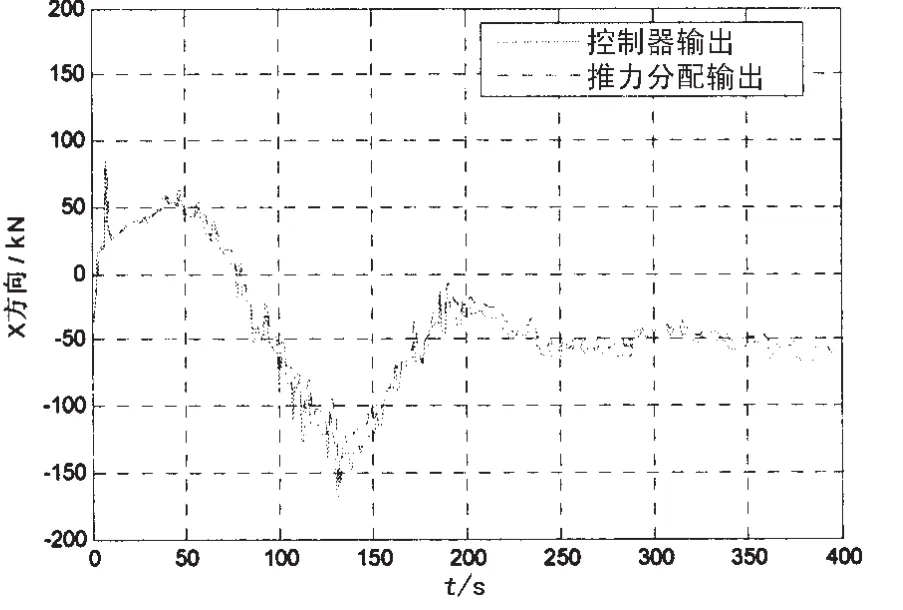
图8 纵荡方向推力误差Fig.8 Thrust errors in surge

如图5-7所示，由于试验过程中所使用的控制器较为简单没有对三个方向的速度进行控制，三个方向在定位过程中均有震荡，但都能满足动力定位系统的控制要求，位置误差在±3 m范围内，艏向误差在±2°范围内，产生上述现象的原因可能是在所建的舵桨组合模型还不够精确，该模型还需进一步优化。

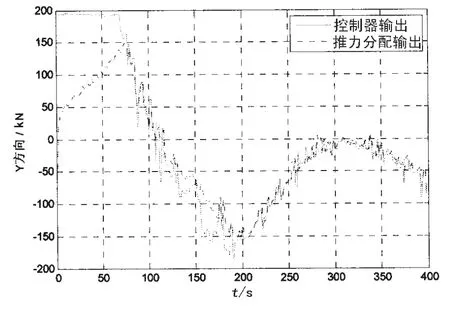
图9 横荡方向推力误差Fig.9 Thrust errors in surge

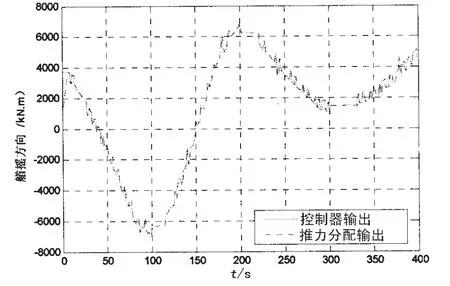
图10 艏摇方向推力矩误差Fig.10 Thrust torque errors in yaw

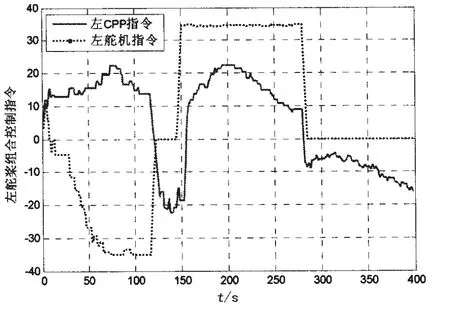
图11 左舵桨组合控制指令Fig.11 Control signals of port propeller-rudder pairs

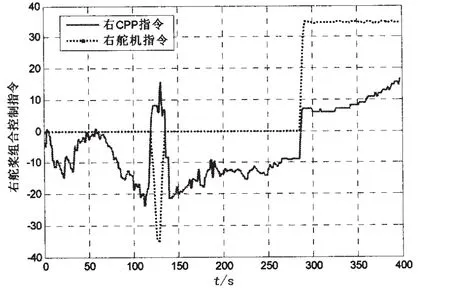
图12 右舵桨组合控制指令Fig.12 Control signals of starboard propeller-rudder pairs

根据实船推进器的物理和机械特性，对推进器的推力变化率、舵角变化率做了限制：左、右主推进器的推力变化率为，左、右舵角变化率为±3°，侧推的推力变化率为从图8-10所示，推力分配的输出基本上能跟随推力分配的输入，推力误差在设计范围内，但在开始几个采样周期内，由于推进器推力变化的限制，推力分配的输入较大造成推力误差较大。

如图11和图12所示：在采样点0-120之间（T1＞0，T2＜0）在推力区域（2），在采样点121-140之间（T1＜ 0，T2＞0）在推力区域（3），在采样点141-160之间（T1＜0，T2＜0）在推力区域（4），在采样点161-280之间（T1＞0，T2＜0）在推力区域（2），在采样点281-400之间（T1＜0，T2＞0）在推力区域（3），由于推力分配的输入有震荡，推力分配策略按所设计的切换逻辑在不同的推力区域切换。由图11-13可看出：左、右主推进器的控制指令较平滑没有出现突变；左、右舵角控制指令较平滑没有出现突变，左、右舵角抖动很小；侧推的控制指令震荡较多，这与推力分配横荡方向输入震荡有关，需要进一步优化滤波器的参数使推力分配的输入较平滑。

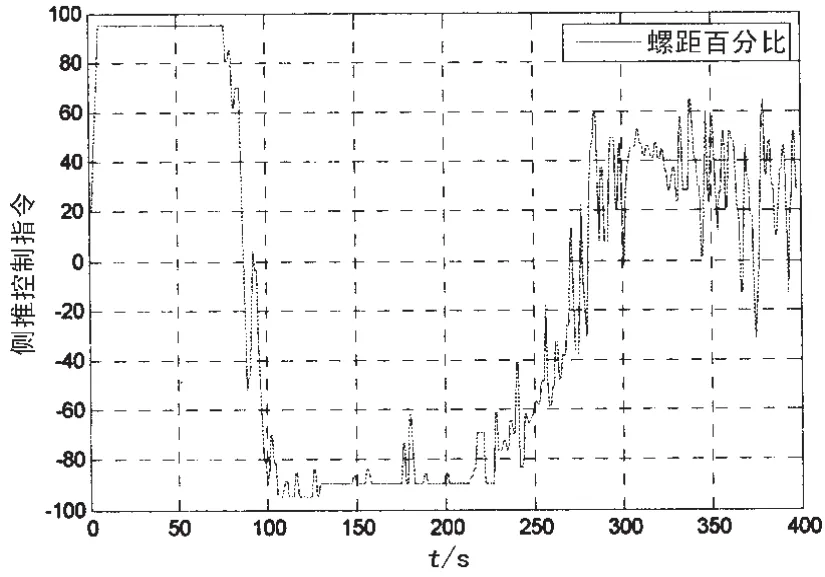
图13 侧推控制指令Fig.13 Control signals of bow thruster

5 结论

把动力定位模式下舵桨组合的推力建模成在不同舵角下与主推进器系柱推力的关系，采用扩展推力的概念把舵桨组合推力描述为一个非凸推力区域。针对舵桨组合非凸推力区域的非线性约束优化推力分配问题，把非线性优化转化为线性优化，采用切换控制把舵桨组合推力分配非线性优化转化成线性二次规划问题，考虑到主调距桨和舵机的机械特性，在优化策略中引入了推力变化率和舵机变化率约束，采用在线优化的方法，方便操作员选择推力分配模式和设置推力分配相关参数。实船试验结果证明了该推力分配策略的有效性，可用于配置舵桨组合的其它类型动力定位船上。

[1]Fossen T I.Handbook in Marine Craft Hydrodynamics and Motion Control[M].John Wiley and Sons Ltd.,2011,398-415.

[2]Fossen T I,Johansen T A.A survey of control allocation methods for ships and underwater vehicles[C].Ancona:14th IEEE Mediterranean Conference on Control and Automation,2006:109-128.

[3]Calabro V,Caiti A.Parametric control allocation for a class of marine vessels[J].Ocean Engineering,2013,58:275-283.

[4]王芳,潘再生,万磊,徐玉如.深水钻井平台动力定位的推力分配研究[J].船舶力学,2013,17(2):19-28. Wang Fang,Pan Zaisheng,Wan Lei,Xu Yuru.Optimal thrust allocation for a dynamically positioned deepwater drilling rig[J].Journal of Ship Mechanics,2013,17(2):19-28.

[5]刘正锋,刘长德,匡晓峰,周德才.模拟退火算法在动力定位能力评估中的应用[J].船舶力学,2013,17(4):376-381. Liu Zhengfeng,Liu Changde,Kuang Xiaofeng,Zhou Decai.Application of simulated annealing algorithem in Dynamic Positioning capability analysis[J].Journal of Ship Mechanics,2013,17(4):376-381.

[6]施小成,魏玉石,宁继鹏,付明玉,等.基于能量最优的组合偏置推力分配算法研究[J].中国造船,2012,53(2):96-103. Shi Xiaocheng,Wei Yushi,Ning Jipeng,Fu Mingyu,Zhao Dawei.Research on group biasing thrust allocation algorithm based on power optimization[J].Shipbuilding of China,2012,53(2):96-103.

[7]Lindegaard Karl-Petter,Fossen T I.Fuel efficient control allocation for surface vessel with active rudder usage:Experiments with a model ship[J].IEEE Transactions on Control Systems Technology,2003,11:850-862.

[8]Johansen T A,Fuglseth T P,Tøndel P,Fossen T I.Optimal constrained control allocation in marine surface vessels with rudders[J].Control Engineering Practice,2008,16:457-464.

[9]Christiaan De Wit.Optimal thrust allocation methods for dynamic positioning of ships[D].Delft:Delft University of Technology,2009:23-47.

[10]Larsen Kjell Erik.Fuel-efficient control allocation for supply vessels[D].Trondheim:Norwegian University of Science and Technology,2012:41-51.

Research on thrust allocation of dynamic positioning vessels with propeller-rudder pairs

YUAN Wei,YU Meng-hong,ZHU Yan
(School of Electronic Information,Jiangsu University of Science and Technology,Zhenjiang 212003,China)

To solve the problem of thrust modeling and nonlinear optimization for propeller-rudder pairs in thrust allocation of dynamic positioning vessels,the non-convex thrust region can be converted into four convex polyhedral sets and Switch Control can be adopted to transform the nonlinear optimization problem into a linear one.Extended thrust can be used in modeling the propeller-rudder thrust with the minimum thrust,rudder angle change and thrust error as the optimization goal,which constrains rate of change of the propeller thrust and rudder angle,error range and magnitude of the propeller thrust.The application of a polygon can convert constrains of thrust range into linear inequality constraints,and switch logic can be designed based on the error in total power and total thrust in the process of switching in different thrust areas.Results of the ship trials demonstrate that the proposed thrust modeling and thrust allocation scheme can meet the requirements of thrust allocation,which is feasible and has a good application prospect.

dynamic positioning;thrust allocation;propeller-rudder pairs;thrust modeling; non-linear optimization;switch control

U664.8

A

10.3969/j.issn.1007-7294.2015.04.007

1007-7294（2015）04-0397-08

2014-09-25

江苏省产学研联合创新资金项目（BY2013066-08）；江苏高校优势学科建设工程资助项目

袁伟（1981-），男，博士研究生，讲师，E-mail:ywjust@163.com；俞孟蕻（1962-），男，教授。