基于撤资的跨市场金融风险传导的实证研究
宋 敏,王丹华,齐 娜
(1.河海大学商学院,南京 211100;2.中国农业银行江苏省分行,南京 211100)
0 引言
目前,国内外已经对跨市场金融风险的传导进行了较为丰富的研究。Calvo和Reinhart(1996)用资产价格相关性分析方法检验了1994年墨西哥比索危机的传染现象,得出亚洲和拉美的新型市场之间的股票和债券的联动性增加的结论。Edwards(1998)聚焦金融市场波动性溢出研究,通过一个扩展的GARCH模型分析了墨西哥波动的传染性,结果表明墨西哥波动明显传染到了阿根廷,但没有传染到智利。蒋序怀、吴富佳、金桩(2006)通过理论模型构建和实证研究,分析了当前我国股票市场、债券市场等狭义资本市场与银行系统的传染效应,得出其风险相互传递的效应关系结论。王宝、肖庆宪(2008)使用DCC-MV-GARCH模型从动态的角度对我国金融市场间的风险传染问题进行了研究,考察了股票市场、债券市场和银行市场间的风险传递特征。本文将基于现有文献的研究基础上,以资本市场撤资为背景,通过使用MGARCH(1,1)-BEKK模型从波动溢出的角度考察我国资本市场与货币市场之间的跨市场金融风险的传导。
1 数据分析与模型建立
1.1 数据的选取与统计性描述
本文选取上证综指与国债指数作为测度我国资本市场波动的基本指标,同时选取信贷市场中的“国内信贷”与“银行间同业拆借市场月加权利率”两个指标作为测度我国货币市场波动的基本指标。本文以2008年为时间节点,选取了我国资本市场撤资发生前的时间(2006年1月至2008年12月)以及撤资发生后的时间(2009年1月至2011年12月)这六年的月度数据进行分析。数据来源于Wind数据库和中国人民银行网站。除回购市场利率(下文记作inrate)以外,本文对上证综指、国债指数以及国内信贷分别取一阶对数差分形式以平稳时间序列,避免伪回归问题的出现,下文中分别用stock、bond、loan表示。
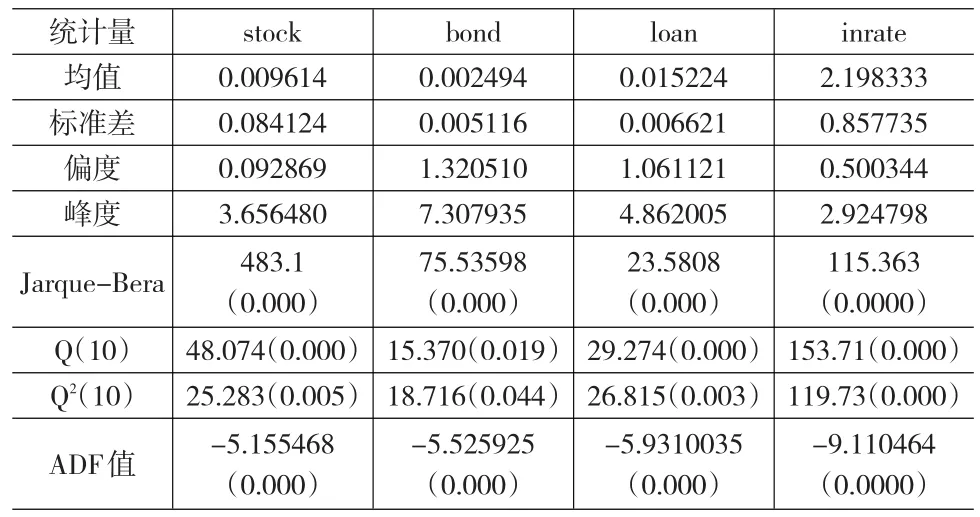
表1 各市场时间序列基本统计特征
表1给出了各变量时间序列的统计性描述。从偏度,峰度来看,各个变量的偏度异于0,峰度均大于3,说明各变量的时间序列呈尖峰厚尾分布。从JB统计量也可以看出变量均为非正态分布。从各序列一阶自回归后得到的残差序列的前10阶自相关的Ljung-Box Q统计量看,变量的时间序列都存在不同程度的序列自相关关系,同时,序列平方的Ljung-Box Q统计量表明各序列的平方也存在显著的自相关,这说明各变量的波动均具有聚集性和时变性,表明本文对各序列建立MGARCH模型是合理的。ADF单位根检验得出所有变量均为平稳,因此在下文的实证分析中可以避免伪回归问题的出现。
1.2 模型的建立
本文采用Engle等提出的BEKK形式的MGARCH模型。假设有A、B两个市场,其二元MGARCH(1,1)-BEKK模型的均值方程和方差方程如下:
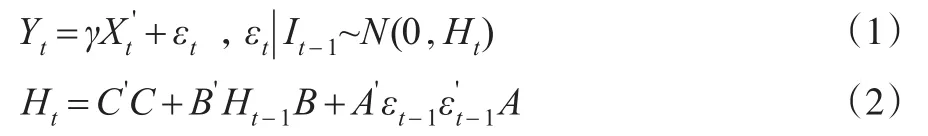
其中,均值方程中的Yt为2×1维因变量向量,Xt是1×(k+1)维自变量向量,γ是2×(k+1)维系数矩阵,It-1表示t-1期的信息集。在方差方程中,Ht为残差项εt的2×2阶条件方差及协方差矩阵。C、A和B都是2×2阶参数矩阵,C为下三角常数矩阵,代表条件方差方程的常数部分,A代表ARCH项的系数矩阵,B代表GARCH项的系数矩阵。对于二元MGARCH(1,1)-BEKK模型,矩阵的具体形式如为:

其中,h11和h22分别表示矩阵A、B的条件方差,而h12和h21则表示A与B之间的条件协方差。对角元素a11,b11,a22,b22表示市场自身波动的持续性,即市场自身前一期残差项平方和前一期条件方差对当期条件方差无影响。非对角元素a12,b12,a21,b21表示市场间的波动溢出,当a12=b12=0时,市场1的条件方差仅受自身前期波动和前期残差的影响,不存在市场2向市场1的波动溢出效应;当a21=b21=0时,市场2的条件方差仅受自身前期波动和前期残差的影响,不存在市场1向市场2的波动溢出效应;而当a12=b12=a21=b21=0时,两市场的条件方差都不受到对方前期波动和前期残差的影响,市场1与市场2间不存在波动溢出效应。
本文采用极大似然估计法(LR)进行参数估计,在条件残差向量εt服从二元条件正态分布的假设条件下,对于含有T个样本的对数似然函数为:

式中,T为样本总数,θ是待估参数向量,由于GARCH模型的对数似然函数形式是非线性的,估计过程我们使用BHHH算法,即利用目标函数的梯度信息进行迭代和优化,目前的研究文献较多采用该方法对多元GARCH模型的参数进行估计。本文首先对两市场分别建立GARCH(1,1)模型得到初步估计参数,并将其参数作为二元GARCH(1,1)模型中对角参数(矩阵C,A,B对角元素)的初始值,非对角元素设定为0。参数收敛水平为0.00001。模型的估计过程通过Eviews6.0和MATLAB7.1实现。
2 实证分析
本文基于二元MGARCH(1,1)-BEKK模型对撤资前与撤资后资本市场(股票市场、债券市场)与货币市场(信贷市场、银行间同业拆借市场)之间的波动溢出效应进行分析,以检验撤资发生后是否存在跨市场风险的传导。表2、表3以及表4、表5分别给出了撤资发生前后资本市场与货币市场之间波动溢出效应的估计结果。
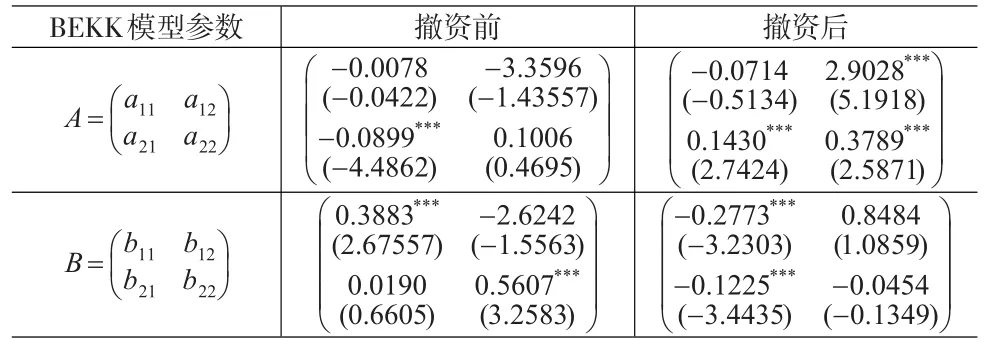
表2 撤资前后股票市场与信贷市场的波动溢出效应
如表2所示,从对角元素来看,股票市场与信贷市场在撤资前后均受到自身前期波动的影响,并且信贷市场受到影响的持续性较大。而从非对角元素来看,撤资前股票市场的前期波动对信贷市场产生了显著的影响,而撤资后,股票市场与信贷市场自身前期的波动都对彼此产生了显著的影响。因此,撤资前后股票市场对信贷市场都具有显著的波动溢出效应,同时从参数值来看,撤资后的溢出效应要大于撤资前的溢出效应。如表3所示,撤资前股票市场与拆借市场仅受到自身前期波动的影响,而撤资后股票市场与拆借市场都受到来自对方前期波动的显著影响,即存在股票市场与拆借市场的双向波动溢出。
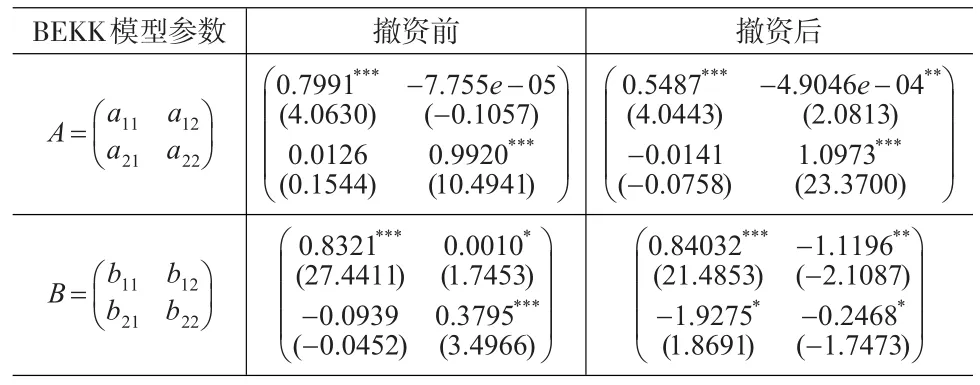
表5 撤资前后债券市场与拆借市场的波动溢出效应
如表4所示,在撤资前后,债券市场与信贷市场均只受到自身前期波动的影响,而并没有受到彼此波动的影响,即两市场在撤资前后都不存在显著的波动溢出效应。如表5所示,从对角元素来看,债券市场与拆借市场在撤资前后均受到自身前期波动的影响,并且都具有持续性。从非对角元素来看,撤资前拆借市场的前期波动对债券市场产生了显著的影响,而撤资后债券市场与拆借市场均受到了来自对方前期波动的影响,但是拆借市场前期波动对债券市场的影响较微弱,同时,债券市场前期波动对拆借市场的影响具有持续性。
3 结论
本文通过MGARCH(1,1)-BEKK模型考察了撤资前后我国资本市场与货币市场间的波动溢出效应,并得出撤资后确实存在资本市场向货币市场的风险传导。
(1)股票市场对信贷市场和回购市场在撤资发生后均产生了撤资发生前不显著的波动溢出,即撤资后存在股票市场向货币市场的跨市场风险传导。
(2)债券市场在撤资前后都没有对信贷市场产生显著的波动溢出,但在撤资后与拆借市场间产生了显著的双向波动溢出。撤资的跨市场金融风险传导实际上就是一个以金融市场为载体的跨市场风险形成、积累、转化和扩散的过程,是撤资风险转化成跨市场金融风险从量变到质变的过程。因此,我国政府要加强对外资流动的监管,构建对跨境资本流动的全面、实时监管体系,增加对撤资监管的及时性和有效性。同时,在金融市场上,面对外资的跨市场运作和撤资风险的跨市场传导,也应当建立一个综合监管的部门,直接形成对撤资情况的监控、报告、分析和干预,并通过良好的金融风险预警机制有效地防范撤资风险的跨市场传递和扩散,避免和降低风险带来的损失,及时减轻我国经济和金融体系的失衡程度,无论对我国金融发展还是整个经济社会的发展都具有重要意义。
[1]郑庆寰,林莉.跨市场金融风险的传递与监管[J].南方金融,2006,(8).
[2]丁浩,许长新.我国现阶段跨市场金融风险的传递载体刍议[J].上海金融,2008,(3).
[3]沈桂龙.跨国公司撤资机理与金融危机的冲击效应[J].社会科学,2009,(9).
[4]姚国庆.金融危机的传导机制:一个综合解释[J].南开经济研究,2003,(4).
[5]卞志村.货币政策的资本市场传导机制[J].南京师大学报(社会科学版),2004,(9).
[6]潘焕焕.次贷危机下境内外证券市场风险传导效应研究[J].山东社会科学,2009,(6).

