一种新的基于TOPSIS的区间数排序法

谭吉玉，朱传喜，张小芝，朱 丽

（南昌大学 理学院管理科学与工程系，南昌330031）

0 引言

区间数是Moore[1]在20世纪60年代提出来的，为描述不确定性问题提供了很大的方便。人们通常使用随机或者模糊分析方法描述不确定性问题，但无论是随机过程的分布函数，还是模糊数学的隶属度函数都是不容易确定的。事实上，用区间数描述复杂的不确定性问题，更符合人们模糊的思维习惯。在区间数基础上建立的区间运算[2]不仅能处理参与计算的量的不精确数据，而且能自动跟踪截断和舍入误差，同时具有计算简单，需要数据量少等优点。不确定性问题的区间分析方法目前成为工程技术领域、管理决策领域及理论研究的热点[3]。

1 基于TOPSIS的区间数排序法

1.1 区间数的概念及其运算法则

1.2 基于TOPSIS的区间数排序原理

TOPSIS是一种逼近于理想解的排序方法。其基本原理，是通过检测评价对象与最优解、最劣解的距离来进行排序，若评价对象最靠近最优解同时又最远离最劣解，则为最好；否则为最差。其中最优解（正理想解）的各指标值都达到各评价指标的最优值；最劣解（负理想解）的各指标值都达到各评价指标的最差值。本文将TOPSIS的原理引入到区间数的排序问题中，为此，需要建立有限个区间数的正理想区间数和负理想区间数的概念。又因为在多属性决策问题中，为了消除不同物理量纲对决策结果的影响，都需要将决策矩阵进行规范化处理，因此，本文所考虑的区间数均包含于[0，1]。

2 属性权重和属性值都为区间数的多属性决策方法

2.1 决策问题

2.2 决策方法及步骤

Step5:按各方案综合属性值的相对贴近度Si的大小对备选方案进行排序和择优

3 实例分析

用文献[9]中的部分数据来说明本文提出的方法，考虑一个大学的学院评估问题。某大学将采用教学(U1)，科研(U2)和服务(U3)为评估属性，对5个学院(Ai，i=1，2，3，4，5)进行评估。属性权重信息为：

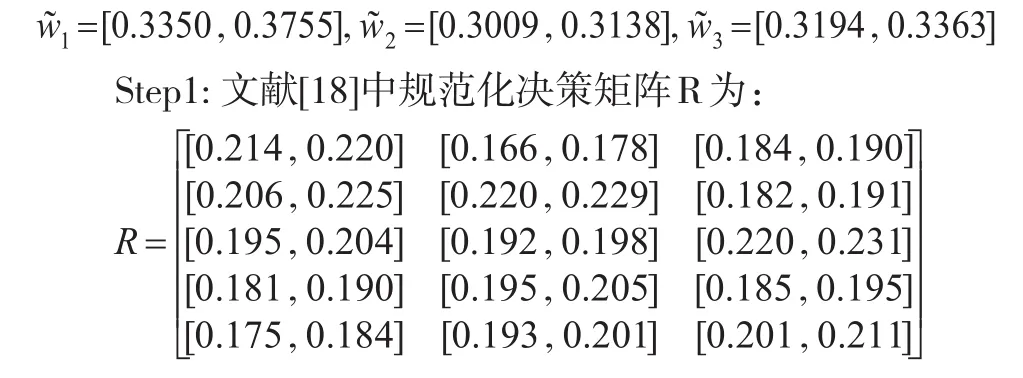
Step2:确定权重

由式(1)和式(2)得区间型权重的正理想区间数[0.3755，，1]，负理想区间数[0，0.3009]，由式(4)算得相对贴近度：C1=0.3541，C2=0.33037，C3=0.3254 ，由式(7)对属性区间型权重的相对贴近度进行归一化得实数型属性权重：w1=0.3602，w2=0.3089，w3=0.3309。

Step3:计算各方案的加权综合属性值

由式(8)计算各方案的加权综合属性值：

Step4:计算各方案加权综合属性值的相对贴近度

表1 五个学院的计算结果

Step5:按Si的大小对五个学院进行排序

因此，这 5个学院的综合排序为：A2＞A3＞A5＞A1＞A4，A2学院的综合排名最高，此排序结果与原文献中的排序结果完全一致，本文中的方法简洁很多。

4 结论

本文基于传统的TOPSIS思想，引入了一个正理想区间数和一个负理想区间数，通过计算每一个区间数的相对贴近度，根据区间数相对贴近度的大小对区间数进行排序。该方法弥补了以前区间数排序法中的许多缺陷。主要有以下四点：①不需要对区间数进行两两比较，从而无需考虑判断矩阵的一致性问题；②能够区分中心数相同的区间数，因而充分考虑了变量取值的分散性；③排序公式简洁、唯一、适用性强，无需根据区间数端点的具体位置分情况讨论；④每一个区间数通过相对贴近度转化成了一个实数，因此可以说建立起了区间数比较关系的一个完备划分。

[1]Moore R E.Interval Analysis[M].Englewood Cliffs,N J：Prentice Hall,1966.

[2]Moore R E.Methods and Applications of Interval Analysis[M].Philadelphia,PA：SIAM,1979.

[3]孙海龙,姚卫星.区间数排序方法评述[J].系统工程学报,2010,25(3).

[4]Nakahara Y,Sasaki M,Gen M.On the Linear Programming Problems with Interval Coefficients[J].International Journal of Computer Industrial Engineering.1992,23(1/4).

[5]徐泽水,达庆利.区间数排序的可能度法及其应用[J].系统工程学报,2003,18(1).

[6]刘健,刘思峰.属性值为区间数的多属性决策对象排序研究[J].中国管理科学,2010,18(3).

[7]徐改丽,吕跃进.不确定性多属性决策中区间数排序的一种新方法[J].统计与决策,2008,19(3).

[8]Cheng C H,Goh C H,Tung Y C A.A Revised Weighted Sum Decision Model for Robot Selection[J].Computers&Industrial Engineering,1996,30(2).

[9]Bryson N,Mobolurin A.An Action Learning Evaluation Procedure for Multiple Criteria Decision Making Problems[J].European Journal of Operational Research,1996,96(3).