粒子侵蚀模型及粒子侵蚀下绝热材料烧蚀数值计算①
徐义华,张燕海,杨玉新,曾卓雄,胡春波
(1.南昌航空大学 飞行工程学院,南昌 330063;2.西安航天动力技术研究所,西安 710025;3.西北工业大学 燃烧、流动及热结构重点实验室,西安 710072)
粒子侵蚀模型及粒子侵蚀下绝热材料烧蚀数值计算①
徐义华1,张燕海1,杨玉新2,曾卓雄1,胡春波3
(1.南昌航空大学 飞行工程学院,南昌 330063;2.西安航天动力技术研究所,西安 710025;3.西北工业大学 燃烧、流动及热结构重点实验室,西安 710072)
从粒子动力学参数出发,分析了粒子与炭化层相互作用机制,导出计算粒子对炭化层作用力,再根据强度理论,推导出粒子对炭化层的侵蚀模型。应用该模型,对实验发动机中粒子侵蚀下的绝热材料烧蚀进行了数值计算,计算中采用了燃气流动与烧蚀耦合计算方法,计算结果与实验结果基本一致,表明所建立的粒子侵蚀可用于固体火箭发动机中粒子侵蚀下绝热材料烧蚀的预估。
航天推进系统;粒子侵蚀模型;绝热材料;烧蚀;数值计算
0 引言
随着高能复合推进剂的推广使用,固体火箭发动机燃气中含有大量的凝相粒子,粒子侵蚀作用不容忽视,尤其是导弹在飞行过程中,高速旋转及急转弯飞行时或在固体火箭发射时出现的高过载,以及某些复杂装药形式造成的高温稠密粒子流,将进一步加剧粒子侵蚀的作用[1]。因此,在固体火箭发动机热结构设计中,必然要考虑粒子侵蚀效应来预估绝热层厚度。目前,在较多的粒子侵蚀模型中,多半是由实验得来的经验关系式[2-6]或是直接引用管道颗粒侵蚀模型[7],在应用上存在一定局限性。更重要的是绝热材料烧蚀过程与其所处的环境和燃气流动状态相关,烧蚀过程与流动是相互耦合的,要真实预示绝热材料烧蚀过程,需要流动与烧蚀耦合计算。在过去研究工作中,已经有一些学者将绝热材料烧蚀与流动进行了耦合计算[8-10],但这些计算中没有考虑粒子侵蚀效应。
本文基于液态粒子与壁面撞击相互作用机制,根据炭化层强度理论,建立粒子侵蚀绝热材料模型,并用该模型对实验发动机绝热材料进行烧蚀计算,计算结果与实验结果进行比较,从而验证粒子侵蚀模型的适用性。
1 粒子侵蚀模型
1.1 粒子与炭化层表面相互作用机制分析
粒子与炭化层表面相互作用的形式是建立炭化层剥蚀计算模型的首要考虑因素。由于固体火箭发动机内工作温度为3 000 K以上,Al2O3的熔点为2 327 K,沸点为4 000 K以上,因此在固体火箭发动机内Al2O3粒子为凝相状态。由文献[11]可知,炭化层表面为固态,粒子对炭化层的侵蚀作用形式,可按液滴撞击固体壁面作用机制来分析。
单个液滴撞击壁面的动力学机制依赖于侵蚀液滴的动力学特性[12],包括液滴直径dp、液滴撞击速度V、撞击角度θ及液滴的物理特性参数,即液滴的动力粘性系数μ、密度ρ、表面张力σ。


图1 液滴与壁面相互作用机制Fig.1 Mechanism of droplet impacting wall
文献[14-15]采用密闭容器法,对固体火箭发动机燃烧室中的凝相粒子进行了收集,分析结果表明,燃烧室中凝相燃烧产物中平均粒度为0.3~7 μm,且呈规则球形。但发生在发动机燃烧室内绝热层的粒子侵蚀,多数为导弹在飞行过程中高速旋转及急转弯时出现的高过载,或者某些复杂装药形式造成的高温稠密的粒子流侵蚀,而凝相粒子聚集会导致粒子直径增大。因此,根据模拟过载状态烧蚀试验发动机尺寸在聚集状态的粒径测量实验[16],粒子直径分布范围0.27 ~300 μm,主要集中在3.0~39.56 μm,即90%的粒子直径小于39.56 μm,质量平均直径d43=20.608 μm。
液态Al2O3密度[17]为2.67 g/cm3。对液态Al2O3表面张力[18]σ1=0.69 N/m。流体动力粘性系数与流体的温度密切相关,而受压强影响较小,文献[19]对多种温度下对Al2O3动力粘性系数进行了实验测量,并对各温度下的粘性系数测量值进行了拟合,得出粘性系数关于温度变化的关系式为
lnμ=11 448/T-8.273 4 Pa·s
(1)
式中T为粒子所处的环境温度(K),这里指炭化层表面温度。
根据液态Al2O3物理特性参数,分别计算出We和Re,计算中取炭化层壁面温度3 000 K。通过计算可知,从粒子直径分布范围来看,反弹、沉积和飞溅这几种机制在粒子与炭化层表面相互作用中都会出现,但由于小粒径占有份额高,粒子法向冲刷速度一般小32 m/s。因此,在建立粒子机械侵蚀模型时,粒子与炭化层表面相互作用机制统一按反弹形式处理。
1.2 单个粒子侵蚀模型
1.2.1 粒子侵蚀力
基于Maw等[20]提出的粒子撞击模型,可得出单个粒子侵蚀壁面的过程,如图2所示,粒子以速度Vi、入射角θi撞击壁面后,受到壁面的法向力Fn和切向力Ft的作用,以反弹角θr、线速度Vr和旋转角速度ωr反弹。在本文计算中忽略粒子的旋转效应。
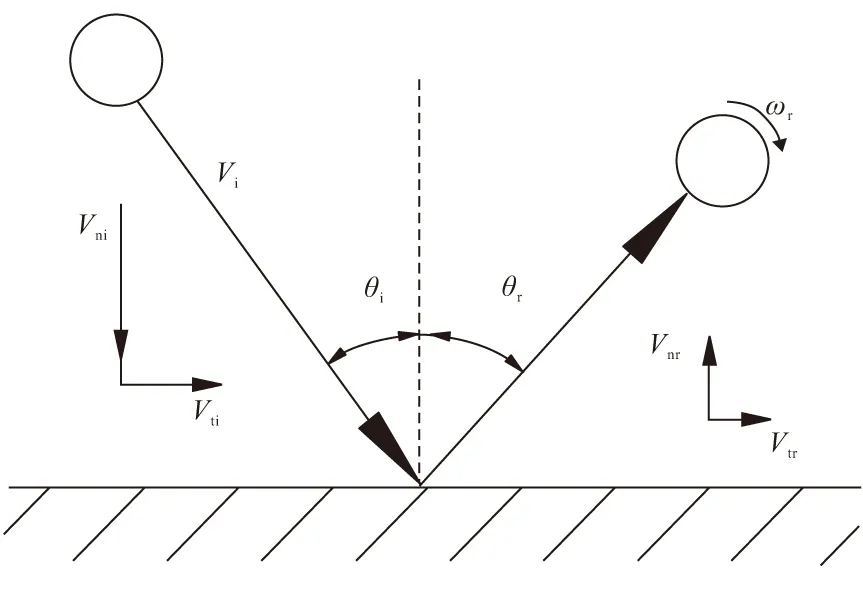
图2 粒子侵蚀示意图Fig.2 Sketch of particle impacting
根据撞击模型,分别定义法向和切向反弹系数为
(2)
(3)
粒子撞击壁面时,受到壁面的法向与切向的冲量作用,定义切向与法向的冲量之比f为
(4)
式中Pn、Pt分别为法向和切向冲量;Fn、Ft分别为粒子接触壁面时的法向和切向分力;Δt为粒子对壁面的作用时间。
根据牛顿定律(动量定理),可得
(5)
(6)
其中,m为粒子质量。由式(5)和式(6)可分别得到粒子对炭化层切向和法向侵蚀力为
(7)

(8)
当粒子撞击炭化层引起的法向力或切向力分别超出炭化层的屈服压应力及剪切屈服应力时,则发生炭化层的机械剥蚀。因此,粒子侵蚀有2种不同形式:一是由法向力引起的变形屈服损失;另一种是由切向力引起的剪切损失。
1.2.2 剪切损失
根据能量守恒原理,对于剪切损失模式,主要由炭化层所受切向应力超出炭化层剪切强度时引起体积损失,每次撞击体积损失可由式(9)计算:
(9)

式(9)的物理意义为粒子对炭化层剪切力功等于炭化层剪切体积损失能,即当粒子侵蚀剪切应力大于炭化层抗剪切强度时,剪切应力与炭化层剪切强度之差乘以粒子作用面积,得到炭化层表面切向作用合力ΔFt;切向速度与作用时间的乘积,得到炭化层表面切向位移ΔS;切向合力与切向位移的乘积,即为粒子在炭化层切向方向所作的功(J);所作功除以炭化层单位体积剪切损失侵蚀能(J/m3),即为粒子在切向所引起的剪切损失体积量。
1.2.3 变形屈服损失
同样,根据能量守恒原理,对于变形屈服损失模式,主要由炭化层所受法向应力超出炭化层抗压强度引起的体积损失,每次撞击体积损失可由式(10)计算:
(10)

式(10)的物理意义为粒子对炭化层表面法向力功等于炭化层变形体积损失能,即当粒子侵蚀法向应力大于炭化层抗压强度时,法向应力与炭化层抗压强度之差乘以粒子作用面积,得到炭化层表面法向作用合力ΔFn;法向速度与作用时间的乘积,得到炭化层表面法向位移ΔS;法向合力与法向位移的乘积,即为粒子在炭化层法向方向所作的功(J);所作功除以炭化层单位体积变形损失侵蚀能(J/m3),即为粒子在法向所引起的变形体积损失量。
单个粒子总侵蚀体积损失Qs为变形磨损和剪切磨损的线性叠加,即
Qs=Qt+Qn
(11)
1.3 粒子流侵蚀模型
当粒子流作用在炭化层表面时,在炭化层表面形成一定的粒子浓度。当侵蚀粒子质量通量为φp时,可由式(12)求得在单位时间撞击在单位炭化层面积上的粒子数量N:
(12)
式中N为单位时间撞击单位面积内的粒子数量,m-2/s;φp为炭化层表面粒子质量通量,kg/(m2·s);ρp为粒子密度,kg/m3;Kp为单个粒子体积,m3。
假设粒子之间互不干扰,则在粒子流侵蚀下,单位时间内在单位面积的炭化层上体积总损失Qtotal为
(13)
式中Qtotal为炭化层线侵蚀率,m/s,即单位时间在单位面积上体积损失量。
将式(9)和式(10)代入式(13),得到粒子对炭化层总的线侵蚀率Qtotal为
(14)
由式(14)可知,粒子对炭化层侵蚀接触面积和持续作用时间是侵蚀计算的2个重要参数。
又由Hertzian方程可得粒子对侵蚀目标面的法向压力Fn为
Fn=zα3/2
(15)

在侵蚀的法向方向,对粒子由动量守恒可得
Fn·dt=-m·dVn
(16)
在粒子侵蚀炭化层过程中,粒子法向速度与法向变形量之间的关系为
(17)

(18)
对式(18)两边同乘dα:
(19)
对式(19)两边积分:
得到
(20)
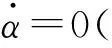
(21)
在压缩变形的终了时刻,接触面积是撞击期间的最大接触面积。假定接触区域为圆形,则由Hertzian定律可得,最大接触面积时的半径rc为
(22)
则最大接触面积为
(23)
定义Δt为粒子侵蚀过程对炭化层压缩持续时间,则由方程(20)可得
(24)
则
(25)
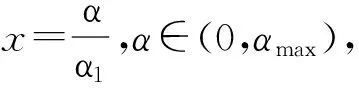
(26)
对方程(26)两边积分:
得到
(27)
由于固体火箭发动机燃气中的粒子对绝热材料EPDM炭化层的撞击是非完全弹性碰撞,需要考虑反弹速度的减小,因而需要引入一个法向反弹系数en(也称恢复系数),炭化层最大法向变形量αmax的计算修正为
(28)
将式(28)代入式(23)和式(27),得最大接触面积Am和持续作用时间Δt的修正计算方程为
(29)
(30)
将式(29)和式(30)代入式(14),可得出粒子对炭化层的机械侵蚀计算模型为
(31)
由式(31)可知,粒子侵蚀下炭化层线侵蚀率与粒子对炭化层的切向和法向侵蚀力Ft、Fn,粒子半径rp,粒子的质量通量φp,粒子侵蚀角θ,粒子侵蚀速度Vp,炭化层对粒子的法向反弹系数en,以及炭化层剪切屈服应力σt和抗压极限应力σn等因素相关。参考文献[21]可知,炭化层对粒子的法向反弹系数en与粒子侵蚀角θ关系式为
en=0.438 6-0.000 5θ+0.001θ2-1.576 6θ3
(32)
由文献[22]可知,炭化层剪切屈服应力σt和抗压极限应力σn分别为
σt=0.01×(1-φ)2σys
(33)
σn=0.102×(1-φ)3/2σys
(34)
式中φ为炭化层孔隙率;σys为炭化层基体物质断裂强度,可参考石墨强度,取值5 MPa。
炭化层粒子侵蚀模型中,体现了当粒子速度和质量通量达到某一临界值时,使粒子对炭化层作用应力超出炭化层极限应力,才发生粒子对炭化层的机械侵蚀作用;也体现了热化学烧蚀消耗炭化层中的碳,使炭化层孔隙增大,削弱炭化层强度,从而加剧粒子侵蚀作用。
1.4 粒子侵蚀热增量
当高温粒子流对炭化层的侵蚀力未超出其极限应力时,粒子对炭化层的侵蚀主要表现为粒子对炭化层的热增量作用。粒子侵蚀热增量的机理主要来源于两个方面:一方面,是粒子撞击动能转换成热能对炭化层的加热;另一方面,是高温的粒子流撞击到温度相对较低的炭化层时,粒子对炭化层的热传递作用,使炭化层加热。文献[23]借鉴液体火箭发动机再生冷却的思想,在理论分析的基础上,设计了一种用于粒子热增量的测试装置。热流测试装置是带有冷却通道的圆形试验模块,并将其安装在固体火箭发动机中进行试验,试验中应用含铝量17%和5%的复合推进剂进行了一系列的实验,经过对实验结果回归分析,得出粒子侵蚀热流关于侵蚀浓度、速度和冲刷角度的计算经验公式:
(35)

2 粒子侵蚀下绝热材料烧蚀计算
2.1 计算模型
由粒子侵蚀下绝热材料烧蚀物理过程分析可知,在燃气流的辐射、对流传热作用下,绝热层温度升高而热解炭化,形成多孔状的炭化层,炭化层在热化学烧蚀消耗下孔隙率增大,其表面在燃气流剥蚀和粒子侵蚀下而剥离,使炭化层表面向下退移。在这种绝热层烧蚀过程中,包含了多物理耦合变化的复杂过程,绝热层烧蚀计算应包括:(1)多组份气相输运、颗粒相运动及辐射换热的发动机内流场计算;(2)在燃气与炭化层交界面上的粒子侵蚀、气流剥蚀和动网格计算;(3)在炭化层内部多孔介质流动、气固异相热化学烧蚀反应、炭化层孔隙率及比表面积更新计算;(4)在炭化层与基体层交界面(即热解面)上的热分解和动网格计算;(5)在基体层内的传热计算。计算框图如图3所示。

图3 绝热材料烧蚀计算框图Fig.3 Frame of calculation on insulation material ablation
2.2 数值计算方法型
控制方程空间离散采用有限体积法,对流项采用二阶迎风格式离散,扩散项采用中心差分格式离散;时间离散采用全隐式方案。方程的求解以通用商业CFD软件Fluent作为计算平台,并通过其提供的用户自定义函数(UDF)编程进行二次开发,对炭化层孔隙率、比表面积更新、炭化层强度、粒子侵蚀力、气流剪切力、热解层的热解速率及炭化层机械剥蚀量进行计算,从而得出炭化层及热解面的网格移动速率,实现燃气与炭化层交界面和炭化层与基体层交界面(热解面)的动态移动过程的模拟。计算中,采用基于压力的分离式算法,为了提高非稳态计算每个时间步中的收敛速度,压力修正采用高效的SIMPLEC算法。计算流程如图4所示,紫色背景部分是UDF实现的功能。计算前,对计算区域进行网格划分,设置边界条件,对计算区域赋初值。在每一时间步的迭代计算中,各模型之间的计算是相互耦合的,燃气与炭化层交界面处的流动参数互为边界条件,由于假设粒子撞击到炭化层表面后反弹,无粒子渗透到炭化层多孔介质中,在炭化层中只考虑气相流动与换热;根据燃气流中的气流参数及撞击到炭化层表面的粒子参数计算气流的剪切应力及粒子侵蚀应力和粒子的热增量;计算出的炭化层多孔介质中各组分的浓度、压力及温度为热化学烧蚀计算提供参数,热化学烧蚀计算出炭化层中碳的消耗量为炭化层中孔隙率及比表面更新计算提供参数,反过来更新后的炭化层孔隙比表面积为下一个时间步内的热化学烧蚀计算提供新的比表面积;通过炭化层孔隙率可计算出炭化层的强度,由炭化层的强度、粒子侵蚀应力和气流剪切应力可计算出炭化层的剥蚀量;根据炭化层的剥蚀率可确定炭化层表面网格退移速率;炭化层多孔介质流动、传热计算为基体层的导热计算提供热流边界,当基体层达到热解温度时进行热解,热分解释放热解气体并吸收热量,以质量、动量和能量源相的形式加入到炭化层多孔介质中;热分解炭化速率可确定热解面网格的退移速率。每个时间步内每次迭代完成后,判断计算精度是否达到要求,如果达到精度要求后累计计算时间,否则继续迭代。累计计算时间后,判断计算时间是否完成,如果完成,则停止计算进行后处理分析计算结果,否则进入下一时间步迭代计算。

图4 绝热材料烧蚀计算流程图Fig.4 Ablation calculation process of insulation material
2.3 计算结果分析
2.3.1 计算区域及其边界条件
为了计算结果能够与实验结果进行对比分析, 本文针对动态烧蚀实验发动机[24]中绝热材料烧蚀进行数值计算。为方便说明计算区域边界条件,作出实验发动机中心对称的二维截面图,如图5所示。流动入口边界条件为燃气质量流率,出口为压力边界条件,发动机壳体设为绝热壁面;绝热材料区域分为炭化层和绝热材料基体层,炭化层上表面为内流界面,为了简化计算,将炭化层到基体层过渡的热解区简化成热解面,炭化层及基体层的侧面设为绝热壁面,即不考虑绝热材料的侧向烧蚀。计算中,坐标原点设置在绝热层初始表面的左端,设绝热材料初始厚度为10 mm,由于炭化层为多孔介质,在Fluent计算中要求预先设定多孔介质区域,预置炭化层厚度为0.2 mm,绝热材料未层化时炭化层孔隙率为0,当其温度达到炭化温度时,初始孔隙率设为0.4。
2.3.2 计算结果分析
对整个计算区域进行初始化温度和压力分别为300 K和101 325 Pa,计算时间为6.0 s。
图6为炭化层结构及其孔隙率分布云图。从图6可看出,炭化层最大孔隙率为0.821,粒子侵蚀部位炭化层孔隙率小于0.6。

图5 计算区域及边界条件Fig.5 Computing domain and boundary condition
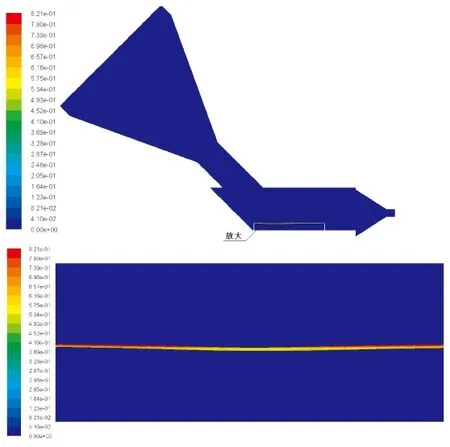
(a)1.0 s

(b)6.0 s
图7为炭化层温度场分布云图。由图7可知,绝热材料烧蚀过程中炭化层温度分布在1 000~3 300 K之间,热解面温度在各烧蚀时刻都在1 000 K左右,炭化层表面温度在3 000 K左右。

(a)1.0 s

(b)6.0 s
图8为每隔1 s各时刻炭化层表面位置计算值与实验值对比。图9为不同位置的瞬态线烧蚀率计算值与实验值对比。

图8 每隔1.0 s各时刻炭化层表面位置 计算值与实验值对比Fig.8 Comparison of computed positions on the surface of charring layer and experimental values at different timesevery other 1.0 s
由图8可知,计算得出的炭化层最低位置点与实验结果一致,都为x=31.5 mm处,烧蚀数值计算得出的最大烧蚀量为5.78 mm,而实验值为5.33 mm,计算误差为8.44%,计算得出最大平均烧蚀率为0.963 mm/s,实验值为0.89 mm/s,计算结果偏大。这主要由于计算中未考虑绝热材料中无机物的相变吸热,而使烧蚀率计算值偏大。
由图9可知,在粒子冲刷部位线烧蚀率在前1 s内迅速增大,然后有所减小,在4.5 s后趋于稳定,这与实验结果所得的规律较为一致,计算结果最大线烧蚀率为1.07 mm/s,而实验结果为1.11 mm/s,误差为3.74%。但从最大线烧蚀率对应的时间来看,计算值为1.4 s,而实验值为2.5 s,即各时刻的瞬态烧蚀率计算误差较大。分析其原因,主要在于各时刻的瞬态烧蚀率的实验数据为0.5 s间隔内的线烧蚀率,而其数值计算已精确到0.1 s间隔内的线烧蚀率。

(a)x=7~31.5 mm (b)x=31.5~56 mm
3 结论
(1)根据液滴与壁面相互作用动力学机制,分析了固体火箭发动机中粒子与壁面相互作用机制主要为反弹形式。
(2)基于Maw等人提出的粒子撞击壁面模型,建立了粒子对炭化层表面的侵蚀力计算模型,并根据能量守恒原理建立了粒子对炭化层机械侵蚀模型,该模型体现了粒子侵蚀力超出炭化层极限应力时,才能发生机械侵蚀作用。
(3)综合考虑流动与烧蚀之间的耦合关系,应用流动与烧蚀耦合计算模型针对动态烧蚀实验发动机构形进行了绝热材料烧蚀数值计算,计算结果分析了各时刻的炭化层结构、孔隙率分布及炭化层温度分布,并得出绝热材料最大平均线烧蚀率和不同烧蚀位置处的瞬时烧蚀率。与实验结果对比分析表明,数值计算结果具有较高的精度。
[1] Melia P F.Flow and ablation patterns in Titan IV SRM aft closures[R].AIAA 95-2878.
[2] Cheung F B,Yang B C,Burch,R L,et al.Effect of melt-layer formulation and thermo-mechanical erosion of high-temperature ablative materials[C]//Proc.Pacific International Conference on Aerospace Science and Technology,Vol.1,National Cheng Kung University,Taiwan,1993:41-48.
[3] Lewis D,Anderson L. Effects of melt-layer formation on ablative materials exposed to highly aluminized rocket motor plumes[R].AIAA 98-0872.
[4] York B J,Sinha N,Dash S M,et al.Steady/transient plume-launcher interactions and progress towards particulate/surface layer modeling[R].AIAA 95-0255.
[5] 何洪庆,严红.EPDM的烧蚀模型[J].推进技术,1999,20(4):36-39.
[6] 李江,刘佩进,陈剑,等. 冲蚀条件下炭布橡胶绝热层烧蚀实验与计算[J]. 固体火箭技术,2006,29(2):110-112,116.
[7] Wirzberger H,yaniv S.Prediction of erosion in a solid rocket motor by alumina particles[R].AIAA 2005-4496.
[8] Chen Y K,Henline W D,Tauber M E. Mars pathfinder trajectory based heating and ablation calculations[J].Journal of Spacecraft and Rockets,1995,32(2):225-230.
[9] Murray A L,Russell G W.Coupled aero heating/ablation analysis for missile configurations[J].Journal of Spacecraft and Rockets,2002,39(4).
[10] Wienholts E,Nguyen P.3D flow thermal analysis of a defect in the RSRM field Joint[R].AIAA 89-2778.
[11] 薛瑞,刘佩进,王书贤. 高温热环境下EPDM绝热材料炭层表面相态试验[J].固体火箭技术,2011,34(4):510-513.
[12] Cossali G E,Coghe A,Marengo M.The impact of a single drop on a wetted solid surface[J].Experiments in Fluids,1997,22:463-472.
[13] Dupays J,Fabignon Y,Villedieu P,et al. Some aspects of two-phase flows in solid-propelland rocket motors[M].Progress in Astronautics and Aeronautics,2006,185:777-788.
[14] Gan X S,Liu P J,Zhao Z B,et al.Collection and analysis of the condensed-phase products of solid propellant by the innovative equipment[R].AIAA 2009-5429.
[15] 赵志博.含铝推进剂凝相燃烧产物的特性研究[D].西北工业大学,2009.
[16] 张胜敏,胡春波,徐义华,等.固体火箭发动机燃烧室凝相颗粒燃烧特性分析[J].固体火箭技术,2010,33(3): 256-259.
[17] Millot F,Glorieux B,Rifflet J C.Measurements of the physico-chemical properties of liquid alumina using contactless techniques[M].Progress in Astronautics and Aeronautics,2006,185:859-883.
[18] Kingery W D.Surface tension of some liquid oixdes and their temperature coefficients[J].Journal of the American Ceramic Society,1959,42(1):6-10.
[19] Bates J L,Rasmussen J J.Effects of additives on volume change on melting,surface tension,and viscosity of liquid aluminum oxide[R].NASA CR-120910,June 1,1972.
[20] Maw N,Barber J R,Fawcett J N.The oblique impact of elastic spheres[J].Wear,1976,38(1):101-114.
[21] 徐义华,胡春波,李 江.炭化层对粒子反弹系数测量实验研究[J].弹箭与制导学报,2011,31(1):119-122.
[22] 徐义华,胡春波,曾卓雄. 三元乙丙绝热材料炭化层结构及力学特性表征研究[J]. 弹箭与制导学报,2012,32(3):237-242.
[23] 张翔宇.粒子侵蚀热增量[D].西北工业大学,2010.
[24] Xu Yi-hua,Hu Chun-bo,Zhang Sheng-min,et al.Experimental research on dynamic erosion of EPDM insulation subjected to particle-laden flow[J].Journal of China Ordnance,2010,6(4):225-233.
(编辑:崔贤彬)
Particle erosion model and numerical simulation of ablation of insulation material eroded by particles
XU Yi-hua1,ZHANG Yan-hai1,YANG Yu-xin2,ZENG Zhuo-xiong1,HU Chun-bo3
(1.School of Aircraft Engineering,Nanchang Hangkong University,Nanchang 330063,China;2.Xi'an Institute of Aerospace Power Technology,Xi'an 710025,China;3.Science and Technology on Combustion,Internal Flow and Thermal-Structure Laboratory,Northwestern Polytechnical University,Xi'an 710072,China)
The mechanism of particle impacting on charing layer was analysed according to the parameters of particle dynamics.The formula that was used to calculate the force acting on charing layer by particle was deduced.The model used to calculate charing layer eroded by particles was set up by the strength theory,which was employed for the numerical calculation of ablation of insulation material in the test motor.The gas flow and erosion coupling calculation method was used.The results of calculation were basically consistent with that of the experiment,which indicates that the particle erosion model can be used for predication of ablation of insulation material eroded by particles in the solid rocket motor.
propulsion system of aerospace;particle erosion model;insulation material;ablation;numerical simulation
2014-01-13;
:2014-02-21。
国家自然科学基金(51266013);航空科学基金(2013ZB56002)。
徐义华(1971—),男,博士,研究方向为航空宇航推进理论与工程。E-mail:xuyihua2003@163.com
V435
A
1006-2793(2015)01-0037-08
10.7673/j.issn.1006-2793.2015.01.007

