Optimized design of biconical liner by orthogonal method
QU Zhong-wei(曲忠伟), YAN Shi-long(颜事龙), SHEN Zhao-wu(沈兆武), MA Hong-hao(马宏昊)
(1.College of Science, Anhui University of Science and Technology, Huainan 232001, China;2.Department of Modern Mechanics, University of Science and Technology of China, Hefei 230027, China)
Optimized design of biconical liner by orthogonal method
QU Zhong-wei(曲忠伟), YAN Shi-long(颜事龙)1, SHEN Zhao-wu(沈兆武)2, MA Hong-hao(马宏昊)2
(1.College of Science, Anhui University of Science and Technology, Huainan 232001, China;2.Department of Modern Mechanics, University of Science and Technology of China, Hefei 230027, China)
A biconical liner was optimized to improve its penetration ability. Its formation and penetration mechanism was studied through numerical simulation and experiments. And the influence of different liner geometry sizes on the jet performance was analyzed using the orthogonal method. The liner formed the high-speed jet with an explosively formed projectile. The small angle 2αremarkably influenced the jet speed which was inversely proportional to 2α. And the liner thicknesst′ and large angle 2βhad highly significant effect on the projectile speed. The liner was optimized att′=0.14 cm, 2α=50°, 2β=135°,N=0.4 or 0.5, when its jet speed respectively is at 6 613 m/s and 6 839 m/s and projectile speed is at 2 247 m/s and 2 095 m/s, steel target penetration is at 8.24 cm and 8.31 cm, and aperture is in 2.12 cm and 2.08 cm. The results show that target is penetrated by the high-speed jet and high-speed projectile resulting into double damages. The penetration ability is improved greatly.
biconical liner; orthogonal design; numerical simulation; jet; explosively formed projectile
The shaped charge structure has strong directional and good damaging properties by taking advantages of energy-gathering effect of explosive. Thus it has been applied to military weapons including the missile and the earth penetrating weapon (EPW) to enhance damaging effect,The liner is, as the carrier of detonation energy transmission, a very important component for the shaped charge structure. With the action of detonation wave, the small angle liner is collapsed to form high-speed shaped charge jet and relatively lower-speed slug. As the liner angle is increased, the jet will slow down, and slug speed up relatively. Herd found that the jet and slug run at the similar speed when the half conical angle is close to 75°, and the liner will form the explosively formed projectile (EFP)[1].
Theoretical studies on the small angle liner have been well developed, for example the general jet theory is suitable for any liner shape and detonation way[2]. The studies show that merely less than 1/3 mass of the liner can form the shaped jet for the small angle liner, but most of the other mass forms the low-speed slugs, and few mass flies away under the role of rarefaction wave. It’s known that the slug has basically no penetration capacity since its speed is normally at several hundred meters per second. In that sense, if the rest 2/3 mass of liner is designed to form penetrable projectile and the jet keeps the high-speed, the shaped charge will be greatly improved in terms of its penetration ability.
This paper designs a biconical liner with large and small angles based on shaped charge jet and EFP characteristics, and analyzes its formation and penetration mechanism by numerical simulation and experimentals. In order to get the best penetration effect, an orthogonal method was used to study the influence of different liner geometry sizes on the jet formation, then to optimize the liner structure. In the end, the penetration ability of the liner was tested through the numerical simulation, and the validity and accuracy of the numerical simulation method was verified by experiments.
1 Orthogonal optimization design for biconical liner
1.1 Design of factors and levels
The liner and its charge structure are shown in Fig.1. The charge diameterDis 5 cm, and liner is made of copper. The five factors are investigated for their influence on the jet formation, which are liner thickness (t′), small angle (2α), large angle (2β), small to large angle ratio (N=d/D) and charge height (H). The design values of various factors at different levels are listed in Tab.1.

Fig.1 Sketch of the shaped charge with a biconical liner
Tab.1 Orthogonal design table

LevelFactort′/cm2α/(°)2β/(°)NH/cm10 024D45900 30 9D20 028D501050 41 0D30 032D551200 51 1D40 036D601350 61 2D
According to a regular test method, it has to conduct 45=1 024 times of tests for the 5 factors at 4 levels in the above Tab.1. However, such enormous tests do cost a large amount of time, man power, materials and financial resources; more importantly, the influence of factors on the jet formation is still hardly identified. Therefore, the orthogonal design method is introduced, and LS-DYNA software is used for designing 16 numerical calculation schemes. By this wayitsaves a lot of calculation resources. The orthogonal design schemes are shown in Tab.2[3].
1.2 Theoretical calculation of biconical liner
Based on the effective charge adiabatic compression method[4], the following assumptions are made specifically:
①Instantaneous full detonation of charge, and rarefaction wave transmitted into the inner detonation product along the inner normal line on surface of charge;
②Detonation product being directionally expanded on the rigid boundary which is based on the initial interface of rarefaction wave, and for establishment of effective charge;
③Closure action of liner being the result of work applied by effective charge toward inner adiabatic expansion.
Based on the assumptions, it defines the effective charge by those angle bisecting lines enclosed in charge sections. Then the liner infinitesimaliis calculated as below[4-5]:
(1)
whereυ0iis the maximal velocity of liner infinitesimal;D0is the detonation rate;biis the thickness of infinitesimal liner;ρ0is the initial density of liner;ρeiis the charge density;beiis the thickness of effective charge of infinitesimal;hiis the travel distance when liner infinitesimal is closed to axis.
It can get the result from geometrical relationship:
(2)
hi=r/cosα
(3)
whereRis the bottom diameter of biconical liner with large angle (R=D/2);ris the bottom diameter corresponding to liner infinitesimali(bottom diameter of biconical liner with small angler=d/2).

Tab.2 Orthogonal design schemes and calculation results
vkisthejettailvelocity, vjisthejettipvelocity, vtistheprojectilevelocity, Listheprojectiledrawratio.
Only whenυ0iis larger than a certainυ0, the bottom of small-angle liner can have an effective recombination with the large-angle liner, instead of flying away under the role of rarefaction wave[4-5]. Take the Group 5 data in Tab.2 as an example, i.e.,α=22.5°,r=12.5 mm,R=25 mm,ρ0=8.93 g/cm3,D0=7.82 km/s,ρei=1.59 g/cm3,υ0=1.3 km/s; and calculate by simultaneous equations (1)-(3) to getυ0i=2.377 km/s>1.3 km/s. Then substitute the other 15-group data of Tab.2 into Eqs.(1)-(3), and get the result ofυ0i>1.3 km/s. That means the designed parameters for the biconical liner in Tab.2 are reasonable, and that the bottom of small-angle liner can be effectively recombined with the large-angle liner.
1.3 Result and analysis of numerical simulation
The finite element method (FEM), which has been embedded in LS-DYNA program, is a highly efficient computation method for explosive mechanics. For the shaped charge structure in this paper, the calculation model contains two parts: explosive and liner. The explosive is a kind of high energy explosive RDX/TNT, so the model of MAT_HIGH_EXPLOSIVE_ BURN and the state equation of EOS_JWL are applied, which have been proved to be suiTab.for detonation calculation[6]. The liner, which is made of copper, will have large plastic deformation under the role of detonation wave, so the model of MAT_STEINBERG and the state equation of EOS_Grüneisen[6]are chosen.
But, FEM can be frustrated by the problems of mesh distortion and sliding plane, so the explosive model will be deleted after completely detonation. Therefore the adaptive grid technique is used for the jet formation of the liner. The grids will be meshed again per microsecond, at size 0.01 cm. The sixteen computational schemes are shown in Tab.2. The state equations are given as[6]:
(4)
(5)


Fig.2 Results of numerical simulation for formation of biconical liner
The numerical simulation indicates that the 16-group biconical liners as designed in Tab.2 form the jet, projectile and slug under the function of detonation. The typical formation process is shown in Fig.2.
Taking the center on the top of main charge as the initiation point (shown in Fig.1), the charge will generate a spherical detonation wave. In Fig.2a, the spherical detonation wave firstly arrives at the liner top. Under the pressure of strong detonation, the small-angle liner gradually approximates towards axis. Redistribution of internal and external energy happens, furthermore, it leads to the formation of high-speed jet by internal infinitesimal while the formation of low-speed slug by external infinitesimal. When the detonation wave reaches the large angle cone, the liner begins flipping as shown in Fig.2a. At this moment, no redistribution takes place, and jet and slug are not separate. They are pressed as a high-speed projectile[5], as shown in Figs.2b, 2c and 2d. And the jet can be fully formed at the time of 23 μs. But, since the jet tip velocity is as fast as several thousands of meters per second, and has great velocity gradient with the tailing velocity, the jet will have to be extended until necking-down (Fig.2b). Besides, because the jet velocity is much faster than slug velocity, the jet will be continuously stretched, fractured and dispersed during its travel, and gradually separated from slug (Fig.2b, Fig.2c and Fig.2d). The large angle liner furthers its flipping and pressing towards axis under the role of detonation wave and inertia, in the meantime, it follows the jet to move forward; actually at that time, the projectile has not yet been separated from jet (Fig.2c). The separation will not be seen until the projectile is completely formed at the time of 133 μs and the moment when the velocity of explosively formed projectile is lower than that of jet (Fig.2d). Afterwards, the projectile will not be deformed any more, and it will stably fly at a certain velocity[5].
1.4 Influence of different liner geometry sizes on jet
The following Tab.3 and Fig.3 show the valuesK1,K2,K3, andK4of jet velocity, projectile velocity and draw ratio at levels as well as the rangeE. The value ofKiat the numberjin the correspondence liner means the sum of the factorjat leveli, recorded asKij[3]. The value ofEis 1/4 of the difference between the maximal and minimal values in the same column.

Tab.3 Jet tip velocity vj m/s

Fig.3 Jet tip velocity
To make a direct analysis on jet tip velocityvj: It’s seen in Tab.3 thatvjreaches the maximal value when factor 1 and 2 at level 1, and when factor 3, 4 and 5 at level 4, namely, the liner thicknesst′=0.12 cm, small angle 2α= 45°, large angle 2β= 135°, proportionNof small angle to large angle = 0.6, and charge heightH=6 cm.
In addition, shown from the rangeEin Tab.3 and also Fig.3, the range of factor 2αis the maximal value; with the increase oft′ and 2α, thevjbecomes approximate linear decrease; and with the increase of 2β,NandH, thevjbecomes gradual growth. So the influence degree of various factors onvjcan be described this way, 2α>t′>H>N>2β. In other words, 2αwill exert the heaviest impact onvjas the main factor, whereas 2βwill exert the lightest impact onvjas the minor factor.
Anyway, the above analysis is only an intuitive analysis. The advantage of this method is simple, intuitive and has less calculation cost. But the error magnitude during experiment and measuring experimental results is not able to evaluate. And the differences of every factor at different levels on the experimental results cannot be determined; it may be caused by change of levels or experimental error. Therefore variance analysis should be applied to meet the requirements, it can determine that the influence of every factor at different levels on experimental results is or isn’t significant[11]. The significance of differences is judged by reliability of analysis, degree of freedom for factors and degrees of freedom for error. Under this reliability of analysis, if the ratio of mean square error for factors to mean square error for error exceeds certain value looked up from the TableFin orthogonal theory, the factor will have significant impact on experimental results[11]. For further researches on the effect of errors and on how different between the factors at levels, it will do the variance analysis onvj. Based on Tabs.2-3, it will calculate the sum of all the data (T), constant terms (Tc), and sum of squares of mean deviations (S1,S2,S3,S4, andS5):
Since the value ofS3is much smaller than others, it can be regarded as an error to test the significance of various factors. Take the degree of freedom (f1,f2,f3,f4andf5) for each factor as 3, in which,f3is degrees of freedom of error.
According to the orthogonal theory, whenα′=0.05 (95% reliability of analysis) andf3=3, the factor’s mean square should be more than 9.28 times of error’s mean square. However herein,F2=9.84 which exceeds over the so-called 9.28. Therefore, factor 2(2α) is verified as the main factor exerting significant influence onvj. So, 2αshould be 45°. Again, whenα′=0.25 (75% reliability of analysis), the factor’s mean square should be more than 2.36 times of error’s mean square. Herein,F1=3.19,F4=2.79, andF5=2.63, which are all larger than 2.36. Hence, judged by 75% reliability of analysis, factor 1, 4 and 5 do have difference, accordingly, the value oft′ will be 0.12 cm,N0.6, andH6 cm, respectively. For the error 2β, the level can be arbitrary value.
To make another direct analysis on projectile velocityvt: it’s shown in Tab.4 thatvtreaches the maximal value when factor 1 and 4 at level 1, and when factor 2, 3 and 5 at level 4, namely, the liner thicknesst′=0.12 cm, small angle 2α=60°, large angle 2β=135°, proportionNof small angle to large angle=0.3, and charge heightH=6 cm.
In addition, shown from the rangeEin Tab.4 and also Fig.4, the range of factor 2βis the maximal value; with the increase of 2β, thevtbecomes approximate linear increase; and for the next large range oft′, with the increase oft′, thevtgradually decreases; for the small range of 2α,NandH, with the increase of 2α, thevtincreases by a little degree, especially thevthas few change when 2αat level 2, 3 and 4. With the increase ofN, thevtdecreases in an exponential way, but by a little degree. The charge heightHhas the minimal effect onvt; despite increasing withH, thevtdifference between maximal and minimal values at the 4 levels is merely about 100 m/s. So the influence degree of various factors onvtcan be described in this way, 2β>t′>2α>N>H. In other words, 2βwill have greatest impact onvtas the main factor, whereasHwill have least impact onvt.

Tab.4 Projectile velocity vt and draw ratio L
For further study on the effect of errors and on how different between the factors at levels, it will do the variance analysis onvt. Based on Tab.2 and Tab.4, it makes the following calculations:
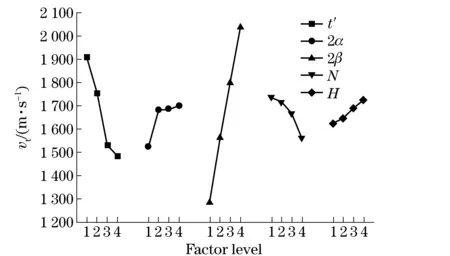
Fig.4 Projectile Velocity
Tab.4 shows that the range value of factor 5 is minimal, and thatS2andS5are several times smaller thanS1,S4andS3. In this sense, it can regardS2andS5as errors to test the significance of various factors. So the additional error will beS6=S2+S5=43 087. Take the degree of freedom (f1,f2,f3,f4andf5) for each factor as 3, and the freedom of errorf6=f2+f5=6.
According to orthogonal theory, whenα′=0.01 (99% reliability of analysis), the factor’s mean square should be more than 9.78 times of error’s mean square. However herein,F1=22.04 andF3=57.8, both of which exceed over the so-called 9.78. Therefore, factort′ and 2βare verified as the main factors exerting significant influence onvt. To that end,t′ should be 0.12 cm, and 2β135°. Again, whenα′=0.1 (90% reliability of analysis), the factor’s mean square should be more than 3.29 times of error’s mean square. Herein,F4=3.4 is larger than 3.29. Hence, judged by 90% reliability of analysis, factor 4 has the differences influence, accordingly, the value ofNwill be preferred as 0.3.
Tab.4 also shows that the projectile draw ratioLis maximal as factor 1 at level 1, as factor 2 at level 3, as factor 3 at level 2, as factor 4 at level 1, and as factor 5 at level 4. Namely, the value oft′ will be 0.12 cm, 2α=55°, 2β=105°,N=0.3 andH=6 cm. Based on the values of rangeE, it concludes with the influence degree of various factors onL:N>H>t′>2α>2β.
Fig.5 below indicates that only factorNhas an obvious regularity impact onL;Ldecreases along with increase ofN. Whent′ increases,Lwill gradually decrease before level 3; however, whent′ further increases,Lwill increase. For the other three factors at various levels,Lhas some changes but no evident regularity. To further prove the conclusion, variance analysis will be done onL, and calculation will be made based on Tab.2 and Tab.4 data:
In view of the minimal range and sum of squares of mean deviation for factor 3, and no evident regularity impact onLby factor 3, theS3is taken as the error to test the factors’ significance. The degrees of freedom for factors (f1,f2,f3,f4andf5) are all 3, and that for errorf3is 3.
According to orthogonal theory, the factor’s mean square should be more than 2.36 times of error’s mean square, whenα′=0.25 (75% reliability of analysis). However herein,F4=2.68 andF5=2.98, both of which exceed over the so-called 2.36. Hence, judged by 75% reliability of analysis, factor 4 (N) and factor 5 (H) have the differences influence at those levels, yet, factor 1 (t′), factor 2 (2α) and factor 3 (2β) have no differences influence at those levels. Accordingly, the value ofNandHwill be 0.3 and 6 cm, respectively. The other three factors can be arbitrarily chosen.
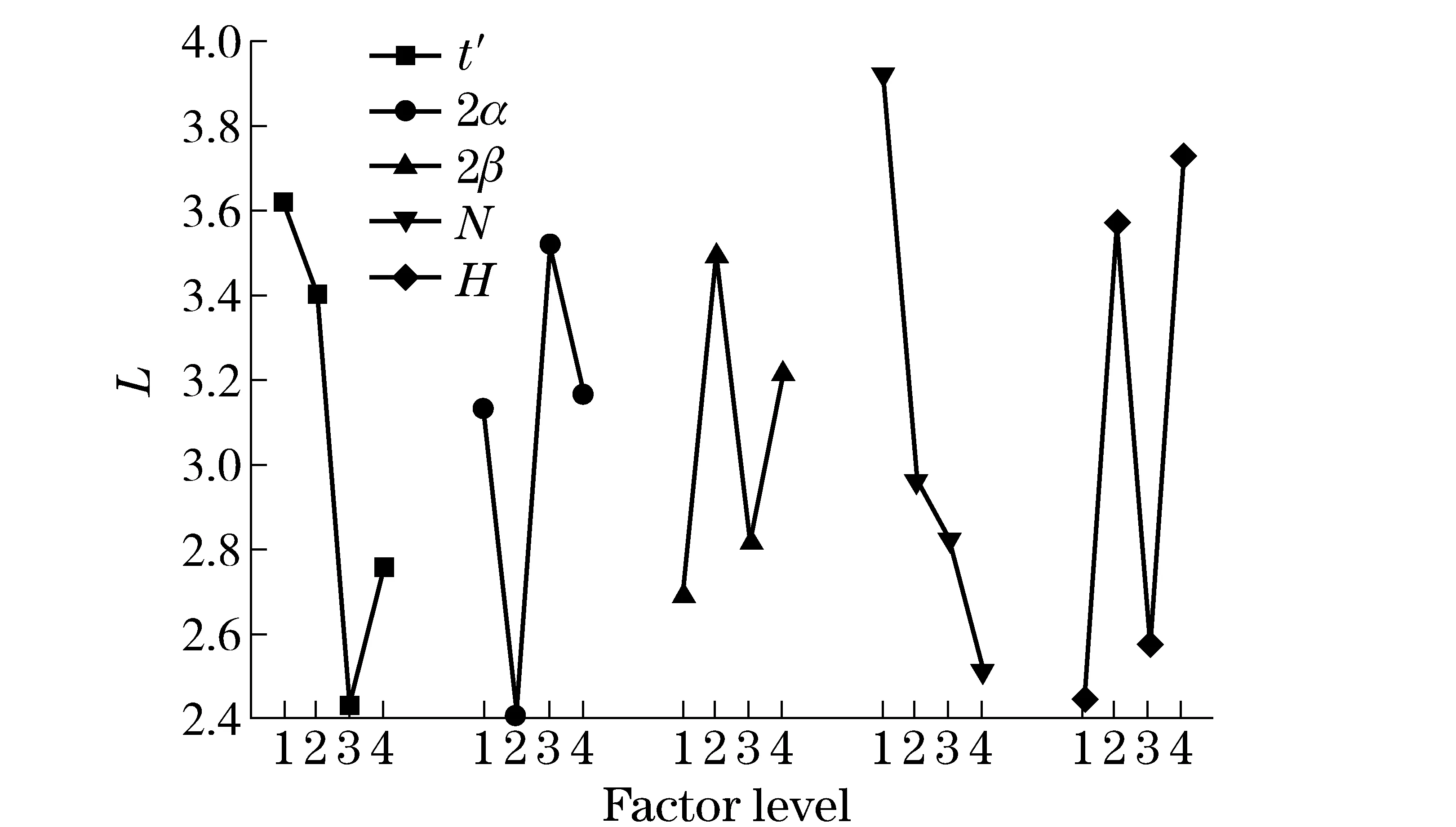
Fig.5 Projectile draw ratio
With the above analyses, it comes to the conclusion that when liner thicknesst′ is 0.12 cm, the jet tip velocityVjand projectile velocityVtcan reach the peak values, and projectile draw ratioLis also the maximal value. However, the smaller thet′ is, the lesser the jet mass becomes. Fig.6 further shows that whent′ is 0.14 cm and 0.16 cm, the jet tip-tail velocity has the biggest difference Δv(Δv=vj-vk), which is conducive to the full tension of jet and deeper penetration of jet. From that, the optimized liner parameters are given in two cases as follows:t′=0.14 cm, 2α=50°, 2β=135°,N=0.4 or 0.5, and charge heightHcan be defined by practical situation. Proceed
with the numerical simulation according to the above parameters (H=5 cm) to get the calculation result of Case 1: jet tip velocityvj=6 613 m/s, projectile velocityvt=2 247 m/s, projectile draw ratio 1.955, and that of Case 2: jet tip velocityvj=6 839 m/s, projectile velocityvt=2 095 m/s, projectile draw ratio 1.295.

Fig.6 Jet velocity difference between tip and tail
2 Experimental verification
The experiment of steel target penetration will be necessary for the shaped charge in Fig.1. The target and the shaped charge are fixed as a whole by tape, and put in an explosion vessel. The shaped charge is detonated by detonator with shock-conducting tube. After the experiment is finished, the target penetration results are measured by liner cutting technology. Nonetheless, due to the limitation of machining, process and accuracy, the real liner is processed according to Tab.5. The experimental and numerical simulation results are shown in Tab.6, Figs.7-8.
It’s seen that the biconical liner is used to achieve almost the same pore in steel target penetration. In contrast, the single conical liner holds the jet penetrating target with large-aperture opening but small-aperture tail. The reasons for same-pore penetration can be described this way:

Tab.5 Experimental parameters of the shaped charge structure
when the target is penetrated, the jet tip firstly strikes the target and forms three-high area (high-temperature, -pressure and -strain), and the subsequent jet continues penetrating through the 3-high area on target; during this process, the jet’s energy distribution changed slowly, and penetration data changed little. The target is in the state of high temperature at this moment. With the weakening of strength, the target is expanded by the action of subsequent large-diameter high-speed projectile. The projectile recovered from the present experiment was just taken from the bottom of the penetrated pore.

Tab.6 Experimental and numerical simulation results

Fig.7 Projectile

Fig.8 Penetration results
The calculation represents the biconical liner with the jet tip velocity of 6 250 m/s and projectile velocity of 1 620.9 m/s. The section 2.4.2 has presented the optimized liner data in two cases and the corresponding calculation results. Under circumstances of the same charge, the calculated depths of target penetration are 8.24 cm and 8.31 cm, and opening apertures 2.12 cm and 2.08 cm. Therefore, the optimized liner structure is verified as the reasonable design parameters.
3 Conclusions
①The biconical liner forms high-speed jet and explosively formed projectile. The significance is not only to guarantee the velocity of jet but greatly enhance the velocity of projectile. The target is penetrated by jet and projectile. By virtue of such double damaging, the penetration ability is improved greatly.
②Among the influencing factors, 2αdemonstrates remarkably in charge of jet tip velocity by an inverse proportional way. Based on 75% reliability of analysis, the jet tip velocity is inversely proportional tot′ and directly proportional toNandH.
③Thet′ and 2βhave highly significant impacts on the velocity of projectile. Specifically, the projectile speed increases with the decrease oft′ and increase of 2β. Based on 90% reliability of analysis, the better the smallerNis. All the parameters are found to have no obvious influence on projectile draw ratio.
④The numerical simulation method is feasible, the error is less than 10% compare with the experimental data. The result of penetrating target is ideal on condition of low-density charge and small standoff distance. So the optimized liner structure is reasonable, and the orthogonal theory method is feasible.
[1] Herd M. Truncated shaped charges[C]∥Proc 15th Int Symp on Ballistics, Jerusalem, Israel, 1995:21-30.
[2] Chou P C, Flis W J. Recentdevelopment in shaped charge technology[J]. Propellants, Explosives, Pyrotechnics, 1986,11: 99-114.
[3] Qiu M, Yan J F, Zhao B H, et al. A finite-element analysis of the connecting bolts of slewing bearings based on the orthogonal method[J]. Journal of Mechanical Science and Technology, 2012,26: 883-887. (in Chinese)
[4] Feng A E, Yang J, Chen P W. Explosion and shock waves[J]. 2004,24: 546-552. (in Chinese)
[5] Li L, Shen Z W, Ma H H. Study on big entry hole bidirectional shaped charge[J]. Chinese Journal of High Pressure Physics, 2011,25: 539-548.
[6] Livermore. LS-DYNA keyword user’ manual[M]. California:Livermore Software Technology Corporation, 2007.
[7] Chen Lang, Long Xinping, Feng Changgen.Detonation of aluminized explosives[M]. Beijing: National Defense Industry Press, 2004. (in Chinese)
[8] Cooper S R, Benson D J, Nesterenko V F. Numerical exploration of the role of void geometry on void collapse and hot spot formation in ductile materials[J]. International Journal of Plasticity, 2000,16: 525-540.
[9] Azami A R, Khoei A R. 3D computational modeling of powder compaction processes using a three-invariant hardening cap plasticity model[J]. Finite Elements in Analysis and Design, 2006,42: 792-807.
[10] Li L, Shen Z W, Li Xue L, et al. Application of SPH method to numerical simulation of shaped charge jet[J]. Explosion and Shock Waves,2012, 32: 316-322. (in Chinese)
[11] Cai Qiang. Orthogonal test on improve the manufacturing parameter of sprcialshaped spring[D]. Shanghai: Shanghai Jiaotong University, 2012. (in Chinese)
(Edited by Wang Yuxia)
10.15918/j.jbit1004-0579.201524.0103
O 383.3 Document code: A Article ID: 1004- 0579(2015)01- 0008-10
Received 2013- 12- 30
Supported by the National Natural Science Foundation of China(51174183); the Anhui Natural Science Foundation of China(1508085ME85)
E-mail: wzqu@mail.ustc.edu.cn
 Journal of Beijing Institute of Technology2015年1期
Journal of Beijing Institute of Technology2015年1期
- Journal of Beijing Institute of Technology的其它文章
- Numerical simulation of the delay arming process of initiating explosive brakes
- Wideband acoustic source localization using multiple spherical arrays: anangular-spectrum smoothing approach
- Influence of eddy current on transient characteristics of common rail injector solenoid valve
- Designing the cooling system of a hybrid electric vehicle with multi-heat source
- Novel miniature pneumatic pressure regulator for hopping robots
- Genetic-algorithm-based balanced distribution of functional characteristics for machines
