Numerical simulation of the delay arming process of initiating explosive brakes
WANG Ru(王茹), WANG Ya-bin(王亚斌)
(National Key Laboratory on Electromechanical Dynamic Control, School of Mechatronic Engineering, Beijing Institute of Technology, Beijing 100081, China)
Numerical simulation of the delay arming process of initiating explosive brakes
WANG Ru(王茹), WANG Ya-bin(王亚斌)
(National Key Laboratory on Electromechanical Dynamic Control, School of Mechatronic Engineering, Beijing Institute of Technology, Beijing 100081, China)
The delay arming process of initiating explosive (IE) brakes for fuse is complex and hard to be verified. A numerical simulation model of IE brakes was established based on the arbitrary Lagrange-Euler method. The model included the structure, the air filed, etc. The simulation boundary conditions were defined, including the contacts, blasting parameters of the explosive and the fluid-solid coupling interface. The simulation results show that the shear pin of the chosen IE can be cut off. When the piston needs to move 0.8 cm, the time set to the delay arming of the IE brakes model is about 40 μs. The maximum displacement of the piston is 1.17 cm. The model provides basis for parameters design and further improvement of IE brakes.
initiating explosive brakes; numerical simulation; ALE; delay arming
An initiating explosive (IE) brake is an insurance device for a fuze system. It is mainly used in the fuze for missiles, rockets and grenades. The delay arming process can be achieved through the time consumed in the combustion of the insurance grains[1]. Fig.1 shows the structure model of an IE brake. The piston of the brake is fixed through the shear pin and the shell is under safety state. When the explosive grains of the IE brake detonate, the shear pin will be cut off. Then the piston will move to the arming location, thus realizing the setting off[2].

Fig.1 Structure model of initiating explosive brakes
At present, thereare no mature theories and formulae for designing and calculating of this mechanism. The experimental method is cumbersome, and the designing process is repetitive. Numerical simulation methods, on the other hand are widely used in the study of explosion. Pawel Baranowski performed numerical simulations on the TNT explosion under a wheel[3]. Todd P. Slavik explicitly modeled the explosive and the air, as well as the blast wave propagating through the arbitrary Lagrange-Euler (ALE) air domain impinges on the Lagrangian structure through FSI[4]. In this tudy, a numerical simulation method is used to represent the delay arming process of IE brakes. The method can effectively analyze the motion process, thus the delay arming time and whether the IE brakes set off can be determined, so as to guide the design and improvement of the devices.
1 Numerical simulation of delay arming process of IE brakes based on the ALE algorithm
The commonly used methods to simulate explosions include sharing the nodes algorithm, the contact-couple algorithm and the ALE algorithm[5-6]. In the numerical simulation process of IE brakes, the meshes’ deformation of explosives and air components is serious. What’s more, after the shear pin is cut off, the piston has a large displacement. So we choose the ALE algorithm to simulate the delay arming process of IE brakes.
Fig.2 shows the finite element model of an IE brake. On the basis of the original 3D model, we can make reasonable geometry cleanups. Air field built in the shell is used to simulate the spreading of explosive gas after the electric squib exploded. * INITIAL_DETONATION card was used in the model to detonate the bomb point which is in the midpoint of the top of the explosives[7], as shown in Fig.3.

Fig.2 3D model of Initiating Explosive brakes
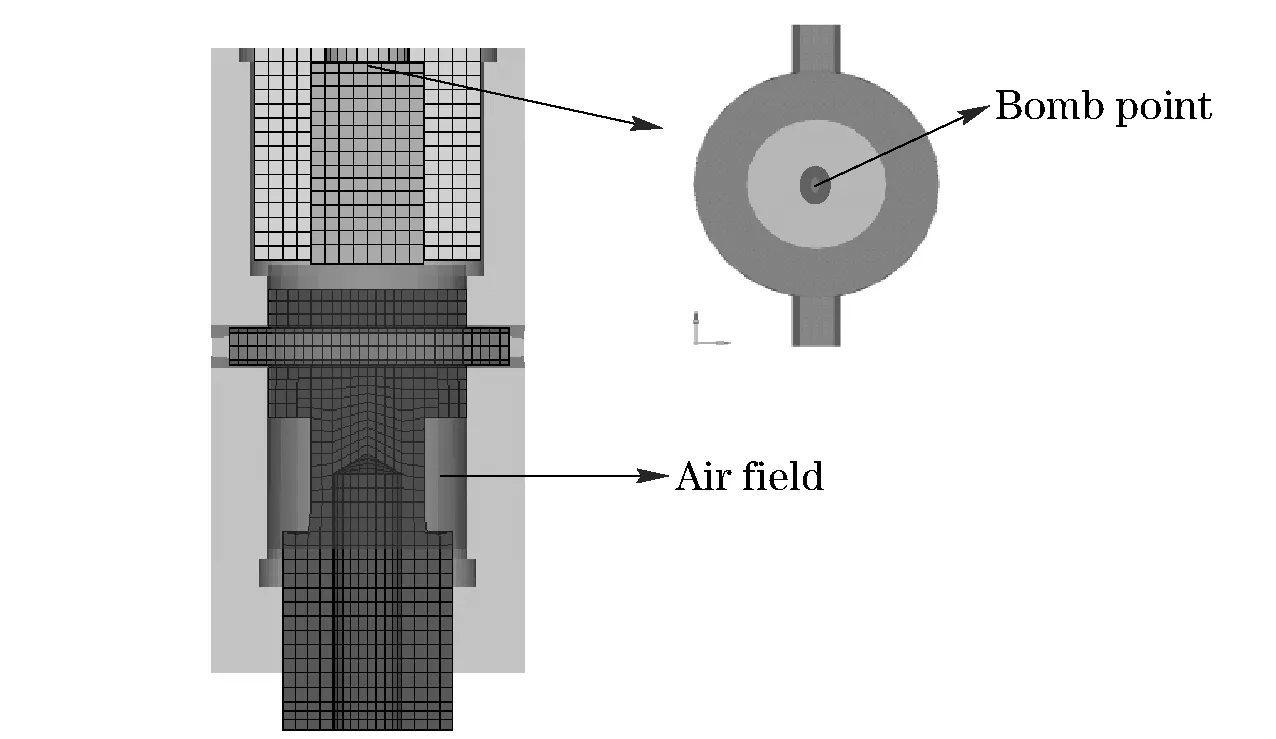
Fig.3 Location of air field and bomb point
Shell, piston and shear pin are all made of isotropically elastic-plastic material constitutive. The material of shell and piston is steel, and the material of shear pin is copper. The explosive used in the IE brake is TNT, whose Material model is defined by the keyword of * MAT_HIGH_EXPLOSIVE_BURN. The equation of state * EOS_JWL should be set in order to describe the energy characteristics of TNT and the physical and chemical processes of combustion[8]. Bomb pressure and detonation velocity of TNT is calculated with the Kamlet empirical equations:
(1)
where PiistheC-Jpressureofexplosion(GPa); Distheexplosivespeed(km/s);φis the characteristic value of explosive;ρ0is the loaded density of explosive;Nis the Moore number of gas products formed by per gram explosive(g-1);Mis the average Moore explosive of gas products(g/mol);Qis the explosion heat.
In the simulation model,we approximately use the output voltage of explosive ignition instead ofPi. The relevant parameters of TNT are shown in Tab.1. The relevant parameters of the TNT material constitutive model are obtained using the Kamlet empirical formula, as shown in Tab.2. The card * MAT_NULL is used to define the fluid model[9]. The state equation formula of TNT explosive(*EOS_JWL)[10]is:
(2)

Tab.1 Relevant parameters of TNT

Tab.2 Equation of the state parameter of TNT
In the calculation process of the IE brake, the air field and explosive are processed as fluid, and Euler elements are adapted to segment them[11]. Piston, Shear pin and shell are processed as solid, and Lagrange elements are adapted to segment them. The card *CONSTRAINED_LAGRANGE_IN_SOLID is used to couple the elements of fluid and solid in order to calculate the interactions between them[12]. The boundary of air field can be processed as Non-reflecting boundary[13].
2 Simulation results
The max stress of the shear pin and its stress nephogram at different times is shown in Fig.4. It counts from the timet=0 μs(pointA) that the bomb point of explosive initiates; at the time oft=2.136 μs(pointB), the shear pin is beginning to be squeezed by the piston; at the time oft=17.889 μs(pointC), the shear pin is curved because of squeezing; at the time oft=31.998 μs(pointD), the shear pin is cut off. The dynamic process of the IE brake’ removing insurance by means of the numerical simulation conforms with the theoretical analysis. At the same time, the shear pin’s being cut off shows that the chosen IE brake can remove insurance smoothly when meeting the design conditions.

Fig.4 Max stress of the shear pin and its stress nephogram at different times

Fig.5 Displacement of the piston
Fig.5 shows the displacement curve of the piston. We can know the time of delay arming based on the curve. For example, according to the installation requirements, the piston finished arming when it moved 0.8 cm. From the displacement curve, the time set to the delay arming of the IE brakes model is about 40 μs. What’s more, if there are no other limit conditions, the maximum displacement of the sliding body is 1.17 cm.
3 Conclusions
In this paper, a numerical simulation method is proposed based on the ALE method to design the IE brake a fuze security device. The method can reacts with what had happened during the process of arming and thus the arming solutions can be judged. The simulation results show that: ① Detonation can drive the piston to cut off the shear pin, and the lock of the piston is lift. ② The time set to the delay arming of the IE brakes model is about 40 μs, when the piston moved 0.8 cm to finish arming. ③ The maximum displacement of the sliding body is 1.17 cm. This numerical simulation method can be used in judging whether the designed device can arm normally, and estimating the time of the delay arming, thus providing a basis for parameters design and further improvement.
[1] Zhang He. The fuze mechanism [M]. Beijing: Beijing Institute of Technology Press, 2007: 126-127. (in Chinese)
[2] An Xiaohong, Zhang Ya, Gu Qing. Fuze design and application [M].Beijing:National Defence Industry Press, 2006:161. (in Chinese)
[3] Pawel Baranowski, Jerzy Malachowski. Numerical investigations of terrain vehicle tire subjected to blast wave [J]. Journal of KONES Powertrain and Transport, 2011, 18(1):23-30.
[4] Slavik Todd P. A coupling of empirical explosive blast loads to ALE air domains in LS-DYNA [J]. IOP Conf Series: Materials Science and Engineering, 2010, 10 (1):1-10.
[5] Wang Wei. Study on damage effects and assessments method of reinforced concrete [D]. Beijing: National University of Defense Technology, 2012. (in Chinese)
[6] Souli M, Shahrour I. Arbitrary Lagrangian Eulerian formulation for soil structure interaction problems [J]. Soil Dynamics and Earthquake Engineering, 2012, 35: 72-79.
[7] Bai Jinze. LS-DYNA3D analysis of theory and practice [M]. Beijing: Science Press, 2005. (in Chinese)
[8] Wu Guiying, Liang Liping, Li Xin. Anomalous response of a circular plate under blast loading with the ALE method [J]. Transactions of Beijing Institute of Technology, 2009, 29 (6):488-491. (in Chinese)
[9] Alia A, Souli M. High explosive simulation using multi-material formulations [J]. Applied Thermal Engineering, 2005, 26:1032-1042.
[10] Chafi Mehdi Sotudeh, Karami Ghodrat, Ziejewski Mariusz. Numerical analysis of blast-induced wave propagation using FSI and ALE multi-material formulations [J]. International Journal of Impact Engineering, 2009, 36 (10/11): 1269 -1275.
[11] Jiang Fei, Han Feng, Wang Jianzhong. Numerical simulation of non-contact explosion by door breaching explosive [J]. Journal of Beijing Institute of Technology, 2013, 22(1):1-4.
[12] Li Lisha, Xie Qingliang, Zheng Quanping, et al. Numerical simulation of contact explosion based on Lagrange ALE and SPH [J]. Blasting, 2011, 28: 18-22. (in Chinese)
[13] Zhao Yanjie. Numerical simulation of structural damage resulting from shock wave of close-in underwater explosion or contact underwater explosion [D]. Dalian: Dalian University of Technology, 2013. (in Chinese)
(Edited by Wang Yuxia)
10.15918/j.jbit1004-0579.201524.0102
O 383 Document code: A Article ID: 1004- 0579(2015)01- 0004- 04
Received 2014- 06-13
Supported by the National Natural Science Foundation of China(11372047)
E-mail: wangyabin@bit.edu.cn
 Journal of Beijing Institute of Technology2015年1期
Journal of Beijing Institute of Technology2015年1期
- Journal of Beijing Institute of Technology的其它文章
- Optimized design of biconical liner by orthogonal method
- Wideband acoustic source localization using multiple spherical arrays: anangular-spectrum smoothing approach
- Influence of eddy current on transient characteristics of common rail injector solenoid valve
- Designing the cooling system of a hybrid electric vehicle with multi-heat source
- Novel miniature pneumatic pressure regulator for hopping robots
- Genetic-algorithm-based balanced distribution of functional characteristics for machines
