面向动平衡对象的柔性转子谐响应分析

丛培田 关 欣

(沈阳理工大学机械工程学院，辽宁 沈阳 110159)

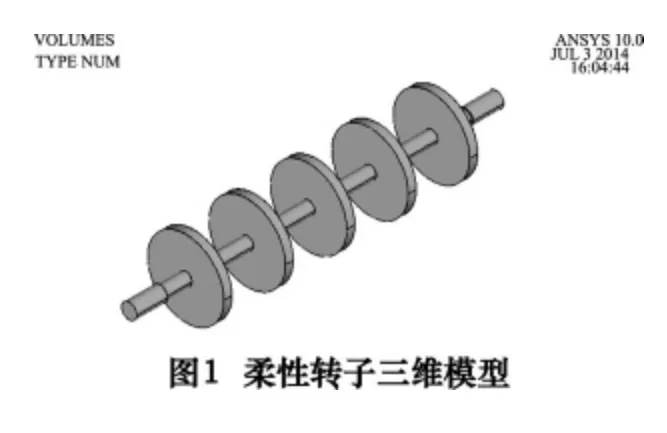
近年来，随着旋转机械转速的不断提高，对于柔性转子的结构动力学特性分析已经必不可少［1］。因此利用ANSYS10.0 软件对一柔性转子模型(如图1 所示)进行静力分析，模态分析及谐响应分析，为柔性转子的现场动平衡研究提供理论依据。

通过3 种分析研究了转子在静力作用下，约束处的受力与某节点处位移的关系，模态分析得出了柔性转子模型的前四阶固有频率值。静力分析与模态分析得出的结论为谐响应分析做准备。由于在转子单盘加谐振力主要产生一阶振型，在转子双盘对称加谐振力偶主要产生二阶振型［2］，而此处通过谐响应分析得出转子在不同的简谐激振力下，某节点处位移随频率变化关系的曲线，得出转子在产生一阶振型的同时也产生了三阶振型;产生二阶振型的同时也产生了四阶振型。由于在一般情况下，转速达不到转子的三阶及三阶以上共振频率所对应的转速，因此如果转子在刚性状态已经达到平衡，那么转子呈柔性状态时，平衡转子一阶振动的同时也平衡了转子的三阶振动;平衡转子二阶振动的同时也平衡了转子的四阶振动［3］。

此外，在转子左侧加简谐激振力，在某些高频下，简谐激振力对右侧节点位移产生的影响大于对左侧节点位移产生的影响。此现象也在谐响应分析中得以验证。

1 柔性转子的静力分析

首先对转子模型进行静力分析。在转子的中间盘上分别加不同大小的静力，观察转子左侧约束处(如图2 所示)一周所受的支反力。

在转子上距离约束处很近的点(0，20，1090)处找到一个相近节点，再读出这一节点的位移(转子左侧约束处一圈的受力与节点位移的关系如表1 所示)。发现在中间盘上加不同静力时，节点处的位移与约束处的支反力成线性关系，因此在实际测量时可用读节点处的位移代替读约束处的支反力(为谐响应分析读取节点位移随频率变化的关系曲线做准备)。

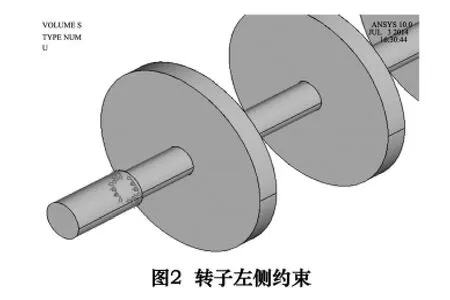
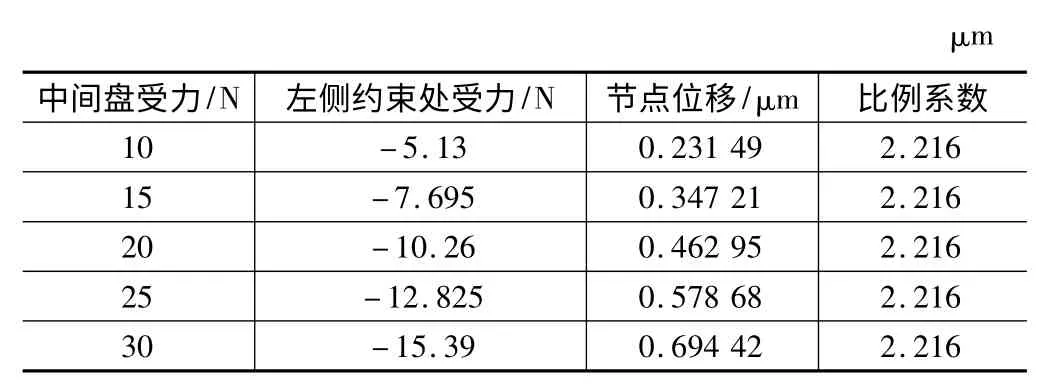
表1 左侧约束处受力与节点位移关系

2 柔性转子的模态分析

对柔性转子的模型进行模态分析，通过分析得到了转子前四阶的固有频率值分别为:33.2 Hz，126.3 Hz，261.4 Hz和413.0 Hz。通过计算仿真数据为下步谐响应分析以及现场试验提供了参考和理论依据，验证了转子的动力学特性，为转子动平衡理论打下基础。

3 柔性转子的谐响应分析

谐响应分析是确定一个结构在已知频率的正弦(简谐)载荷作用下结构响应的技术。分析的目的是计算出结构在不同频率下的响应并得到响应值(通常是位移)对频率的曲线［4］。

此次分析运用谐响应分析中的模态叠加法，选取转子轴上的8 个点(如图3 所示)，得出各点处与其最近的节点的位移随频率变化的曲线图。

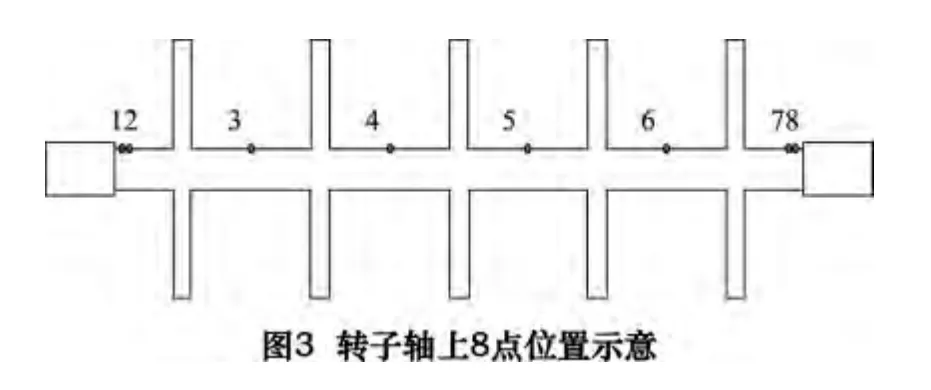
其中各点的坐标为:1 点(0，20，1090);2 点(0，20，1080);3 点(0，20，901.5);4 点(0，20，700.5);5 点(0，20，499.5);6 点(0，20，298.5);7 点(0，20，120);8点(0，20，110)。

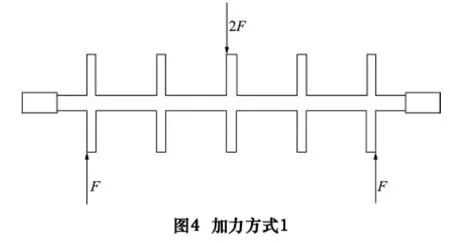
(1)转子在一盘加-10 N 简谐力，三盘加-20 N简谐力，五盘加-10 N 简谐力时，转子主要振型为一阶和三阶(其中负号表示所加力指向圆心)。

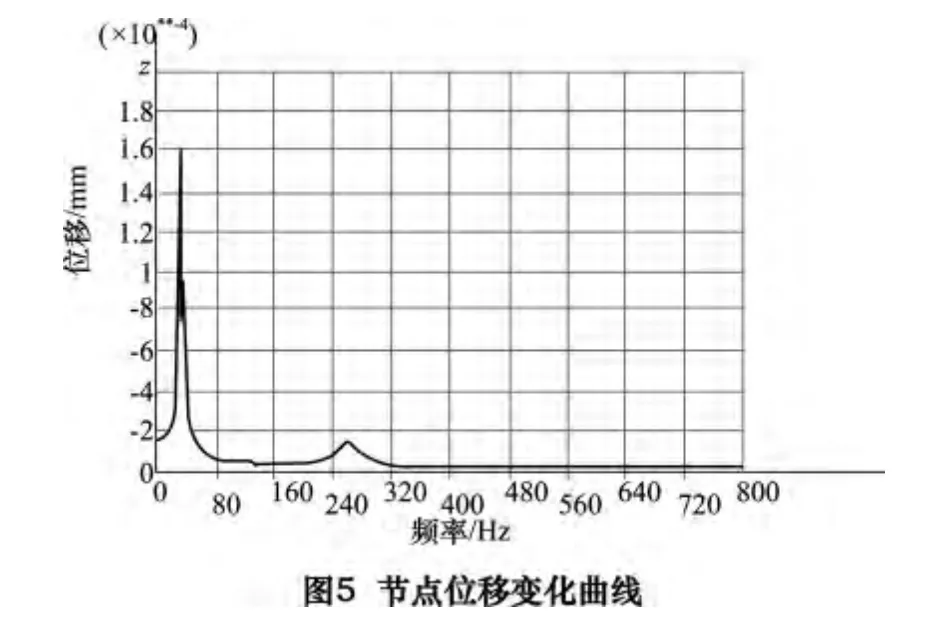
假设转子在刚性状态已经达到平衡，随着转速的增加，转子呈柔性状态，如果此时还存在一阶和三阶不平衡振动，那么存在的不平衡量位置只能为图4 所示的形式。这样通过谐响应分析，分别在转子一盘加-10 N 简谐力，三盘加-20 N 简谐力，五盘加-10 N 简谐力(如图4 所示)来模拟存在的不平衡量，观察转子不同部位的节点位移。图5 所示为转子受上述简谐激振力时，转子7 点(0，20，120)的最近节点位移随频率变化的曲线(由于轴上点都可成功显示出一阶和三阶节点位移随频率变化的曲线，此处为方便，从其中挑选一点做说明)。图中F=10 N。

得出结论:如转子在低速(刚性)时已达到平衡，在高速呈柔性时加上述谐振力(不破坏低速平衡)，转子主要产生了一阶和三阶的振型，所对应的频率也为一阶和三阶的固有频率。说明按这种方式配重能够平衡转子一阶振动的同时也平衡了转子的三阶振动。

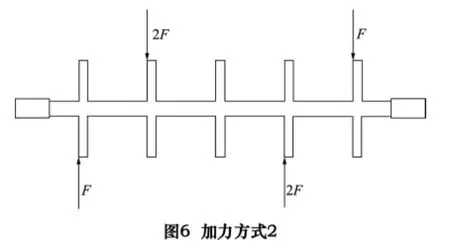
(2)转子在一盘加-10 N 简谐力，二盘加-20 N简谐力，四盘加-20 N 简谐力，五盘加-10 N 简谐力时，转子主要振型为二阶和四阶(其中负号表示所加力指向圆心)。

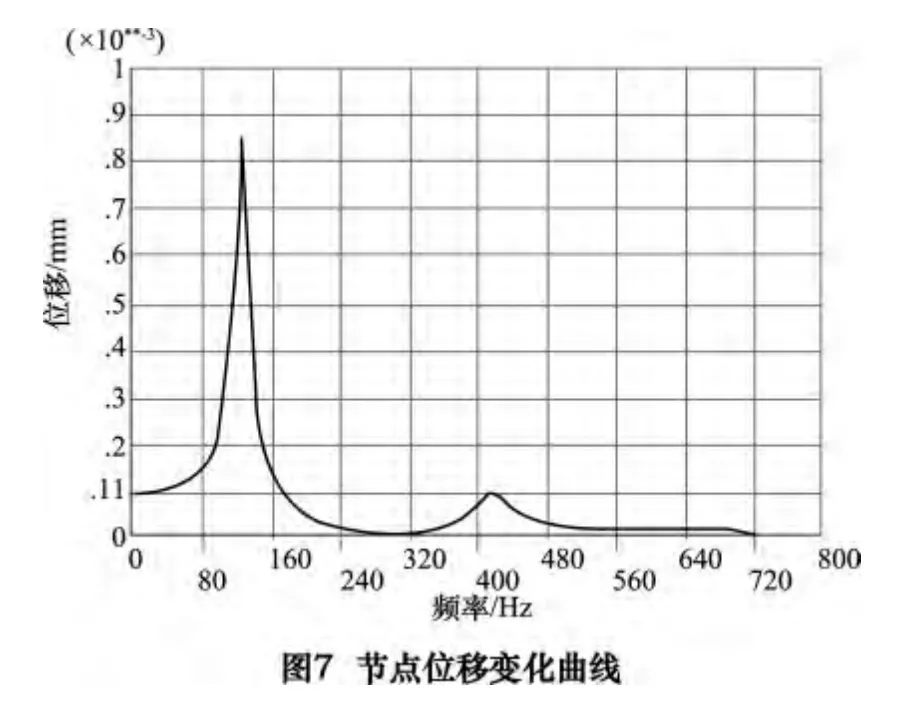
假设转子在刚性状态已经达到平衡，随着转速的增加，转子呈柔性状态，如果此时还存在二阶和四阶不平衡振动，那么存在的不平衡量位置只能为图6 所示的形式。这样通过谐响应分析，分别在转子一盘加-10 N 简谐力，二盘加-20 N 简谐力，四盘加-20 N 简谐力，五盘加-10 N 简谐力(如图6 所示)来模拟存在的不平衡量，观察转子不同部位的节点位移。图7 所示为转子受上述简谐激振力时，转子5 点(0，20，499.5)的最近节点位移随频率变化的曲线(由于轴上点都可成功显示出二阶和四阶节点位移随频率变化的曲线，此处为方便，从其中挑选一点做说明)。图中F=10 N。

得出结论:如转子在低速(刚性)时已达到平衡，在高速呈柔性时加上述谐振力(不破坏低速平衡)，转子主要产生了二阶和四阶的振型，所对应的频率也为二阶和四阶的固有频率。说明按这种方式配重能够平衡转子二阶振动的同时也平衡了转子的四阶振动。

(3)转子在左侧二盘加简谐力时，在某些频率下，谐振力对右侧节点位移的影响大于对左侧节点位移的影响。

通过谐响应分析，在转子左侧二盘上加10 N 的简谐激振力，看转子左右两侧对称的点1(0，20，1090)和点8(0，20，110)距离最近节点的位移随频率的变化。通过比较发现，在转子左侧加谐振力时，在某种较高频率下会出现谐振力对右侧位移的影响大于对左侧位移的影响。图8 所示为在转子左侧二盘加10 N 简谐力时，两侧节点的位移随频率变化曲线的比较。

得出结论:在一般情况下，转子的受力与节点位移的变化成正比关系，即在某侧施加谐振力后，对本侧节点位移的影响大于对另一侧的影响。但在柔性转子一侧加上简谐激振力后，在某些高频率下，会出现简谐力对另一侧节点位移的影响大于对本侧节点位移的影响。通过此结论，可以解释一些实际中出现的特殊情况，也可为避免此现象发生提供理论依据。

4 结语

本文利用有限元ANSYS10.0 软件，以柔性转子为研究对象，对柔性转子进行静力分析，模态分析和谐响应分析。得出了转子约束处的受力与某节点处位移成线性变化的关系和转子的各阶固有频率以及转子在不同的简谐激振力下产生的位移随频率变化的关系曲线。说明了按某些配重方式，能够平衡转子在低阶(刚性)的振动，同时转子在高阶(柔性)的振动也得以消除。在转子一侧加简谐激振力，在某些频率下，谐振力对另一侧节点位移的影响大于对本侧节点位移的影响。利用ANSYS 软件对动平衡对象进行谐响应分析，具有较高的理论说明作用，为现场动平衡研究提供理论依据。

［1］杨国安.转子动平衡使实用技术［M］.北京:中国石化出版社，2012.

［2］丛培田，关欣，韩辉，等.多级柔性水泵转子的动力学有限元分析［J］.工具技术，2013，47(12):48 -50.

［3］丛培田，杨克振，韩辉，等，多级柔性水泵转子的两速三面动平衡方法研究［J］.机床与液压，2013，41(15):93 -94，150.

［4］刘伟，高维成，丁广滨.ANSYS12.0 宝典［M］.北京:电子工业出版社，2010.