基于本征模函数和广义回归网络的刀具声发射信号诊断*

王 宇 喻俊馨 钟 雯 刘小莹 宋春华

(西华大学机械工程与自动化学院，四川 成都 610039)

机床刀具在切削过程中不可避免的存在磨钝和破损等现象，刀具磨损会严重影响生产效率和加工质量。因此，刀具故障诊断对于提高切削加工的自动化程度和产品质量具有重要意义［1］。

目前，刀具磨损和故障监测主要有两种基本方法:直接法和间接法。直接法，如观测和光学法，可以发现由磨损引起的刀具实际几何变化。然而，由于刀具和工件的连续接触以及冷却液的存在，直接法通常很难实施。间接法则通过测量与刀具磨损状态密切相关的特征信号实现。最常见的间接法包括分析加速度信号、动态力信号和声发射信号。傅里叶变换(fast fourier transform，FFT)和小波广泛应用于间接法。其中，频域的二次谐波是刀具磨损的有效特征，然而近年来研究频率成分作为刀具故障特征已逐渐被忽视，另一个途径是利用频域的能量。直接利用FFT 的困难还在于:(1)由刀具磨损或故障引起的几何形状变化能否在频谱上反映出来;(2)FFT 难于处理非线性和非平稳数据，而加工过程通常被描述为一个非线性和非平稳过程。近来涌现出的时频分析方法——经验模态分解［2］(empirical mode decomposition，EMD)非常适于处理切削加工过程的非线性和非平稳信号。

本文以经验模态分解、广义回归神经网络和果蝇优化算法为工具，研究刀具磨损与其声发射(acoustic emission，AE)信号的能量关系。

1 理论与算法

1.1 经验模态分解

EMD 方法本质上是对一个信号进行平稳化处理，该方法具有自适应性、完备性、正交性等特点。EMD从信号的时间特征尺度出发，通过一种“筛(sifting)”过程将信号中不同尺度的波动或趋势分解出来，产生一系列具有不同特征尺度的本征模函数(intrinsic mode function，IMF)与一个残余项之和，从而反映信号的内部特征。通常，EMD 方法分解出来的前几个IMF 分量往往集中了原信号中最主要的信息，这是由IMF 的本性所决定的，因为它总是把最重要的一些信息先提取出来。从这个角度上讲，EMD 方法可以看作一种新的主成分分析方法。

EMD 的自适应性表现分解过程中基函数自动产生、自适应多分辨率和自适应滤波，即EMD 等价于一个自适应的带通滤波器组，原信号x(t)分解成一组分量信号:

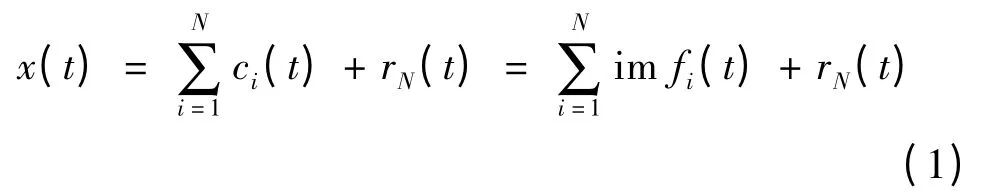
每阶im fi(t)是原信号在特定频率段上的分量，而残余分量rN(t)的能量很小，在计算信号总能量时可忽略不计。原信号的总能量可以表示为:

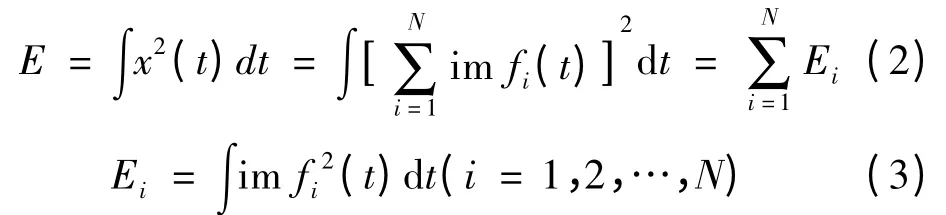
全部IMF 都是相互近似正交:

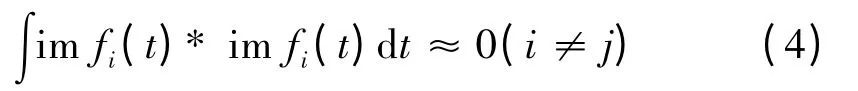
每一阶IMF 的能量都来自原信号，所以所有分量信号的能量总和等于原信号的能量。计算原信号在每一个自适应频段上的能量分布，并对各阶IMF 分量进行归一化处理，提取特征向量:

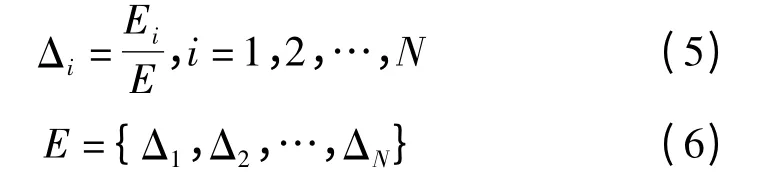
各阶IMF 的能量分布状态能够自适应地反映原信号的频率-能量状态。

1.2 广义回归神经网络

广义回归神经网络(general regression neural Network，GRNN)是一种基于非线性回归理论的监督式径向基神经网络模型［3］。GRNN 以概率密度函数取代方程，直接计算出因变量对自变量的回归值。该模型由4 层网络构成，依次为输入层、模式层、求和层和输出层。输入层只传递输入向量到径向基层，隐含层中神经元个数由所描述的问题而定，通常传递函数采用高斯函数:

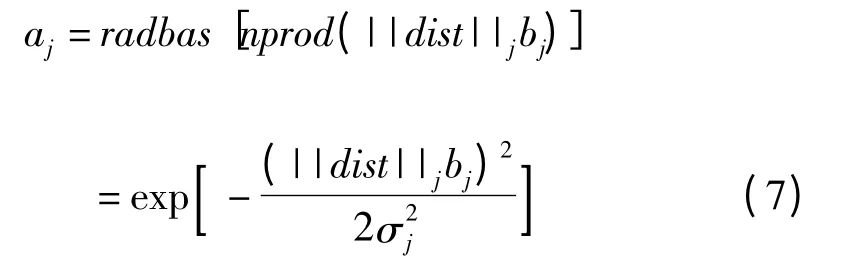
式中:aj为经过高斯函数传递后的网络输出;nprod 表示规范化点积权函数，是线性输出层的权值函数;||dist||为欧氏距离函数，即该层权值函数;bj为第j个隐含层与光滑因子有关的阈值;σj为光滑因子，即分布系数，它决定第j 个隐含层位置处基函数的形状，σj越大基函数越平滑。

GRNN 网络的学习过程实际上就是确定光滑因子的过程，且学习全部依赖于数据样本，能够收敛于样本量聚类较多的优化回归面，在训练样本较少时效果也较好。GRNN 网络的逼近能力、分类能力和学习速度比BP 网络有较强的优势，对于线性或非线性的回归问题都有很好的处理能力。GRNN 网络人为调节的参数少，只有一个阈值及光滑因子可以对GRNN 性能产生重要影响。光滑因子值越小，网络对样本的逼近性也就越强;光滑因子值越大，网络对样本数据的逼近过程也就越平滑，但误差也相应增大。因此，选择恰当的光滑因子是分类的关键。

1.3 果蝇优化算法

文献［4］提出了一种基于果蝇觅食行为推演出的寻求全局最优化的果蝇优化算法(fruit fly optimization algorithm，FOA)。该算法模拟嗅觉发达的果蝇从空气中的气味中获得食物源的方向，飞近食物位置后又使用敏锐的视觉发现食物与同伴聚集的位置，并且往该方向飞去最后寻找到食物。FOA 算法的基本流程如表1 所示。

表1 基本果蝇算法流程图

研究表明，果蝇算法具有速度快收敛稳定等优点。从数学上讲，GRNN 光滑因子的确定本质是一个优化问题，即寻找一个最优的光滑因子，使得训练样本的GRNN 输出值与实际值的均方差最小。因此，为了减少模型参数选择的人为因素影响，降低网络结构设计的随意性。本文将采用果蝇优化算法对GRNN 模型的光滑因子进行优化，求解最佳模型参数。

2 基于IMF 和FOA -GRNN 的刀具诊断方法

刀具AE 信号具有很强的非平稳性，利用IMF 能量分布能够有效地揭示原信号内在的特征，提取信号的特征向量。通过FOA 算法对GRNN 模型光滑因子参数进行优化，可以解决GRNN 拓扑结构难以确定的问题，并且保留GRNN 非线性映射能力强、容错性和鲁棒性高的特点，具有较高的预测精度和稳定性，并且FOA 编码简单、易于实现，建模所需参数也易于测取，有利于工程应用推广。

基于IMF 和FOA -GRNN 的刀具故障诊断方法流程图如图1 所示。

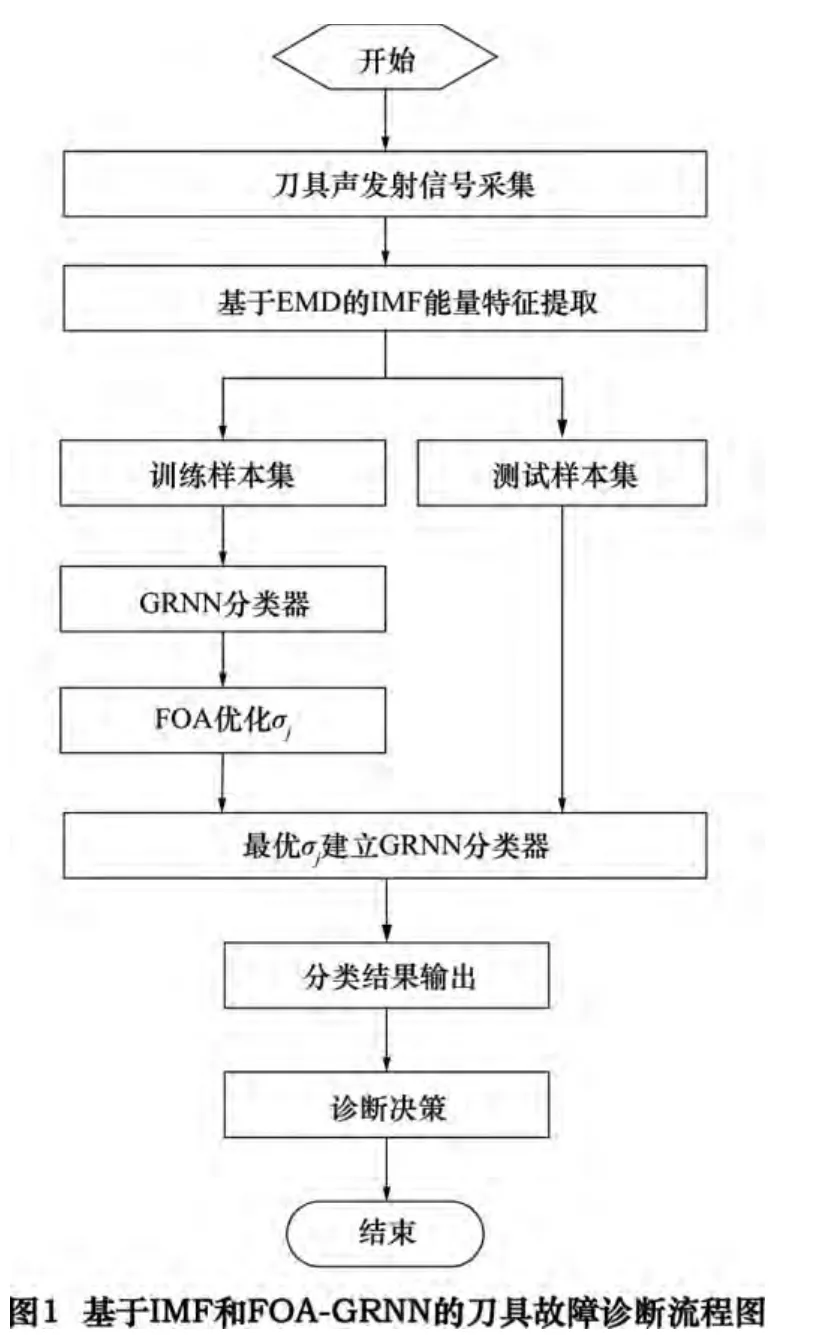
具体诊断步骤实施如下:

(1)分别在刀具正常和故障2 种状态下，以采样率fs各采集m 组数据，得到2m 组声发射信号。

(2)在2 类数据中，分别随机选出k 组数据作为训练数据，将剩下的m -k 组数据作为测试数据。分别对k 组训练数据中的每个信号进行EMD 分解，选取相同数目的IMF 分量，计算其能量，形成故障特征向量A，组成训练样本集;对测试数据进行同样处理，得到故障特征向量B，组成测试样本集。

(3)将由故障特征向量A 组成的训练样本集作为GRNN 的输入，利用FOA 优化GRNN 的σj。

(4)使用优化后的σj建立GRNN 故障分类器。

(5)利用建立好的故障分类器，输入由故障特征向量B 组成的测试样本集，对其进行故障分类和诊断，判断刀具的状态。

3 实验分析

3.1 实验系统

刀具状态分为刀具正常切削、刀具磨损和刀具破损等3 种主要状态，本实验只考虑刀具正常切削和磨损两种情况，采集刀具切削状态AE 信号(刀具正常和刀具磨损)各30 组。实验参数如表2 所示。

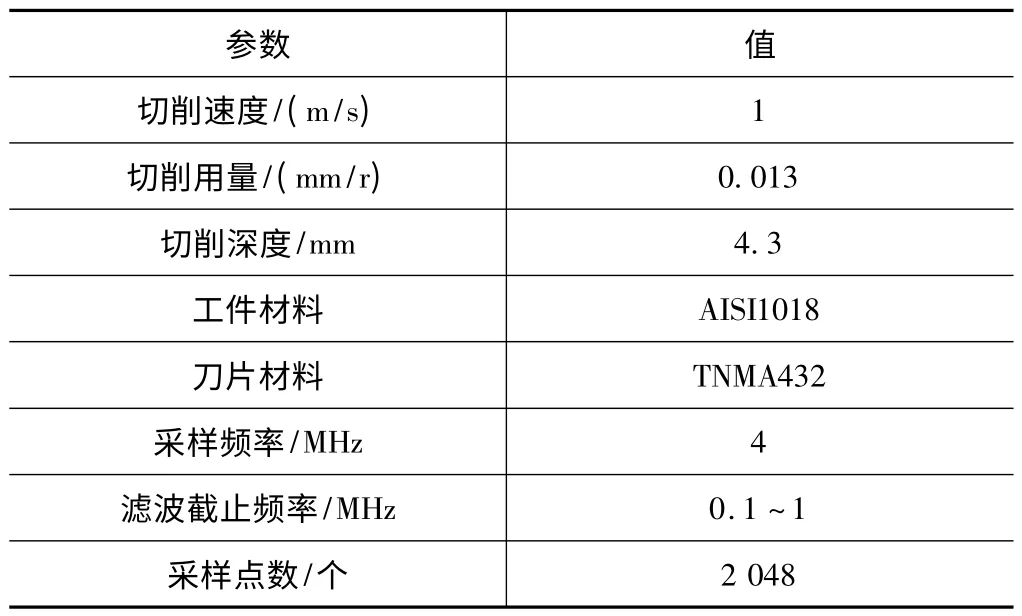
表2 实验参数

当刀具切削时，刀具磨损对AE 信号各频率成分的增强和抑制作用发生变化，通常它会明显对一些频率成分起增强作用，而对另外一些频率成分起抑制作用。因此信号的各频带能量中包含了丰富的刀具故障信息，通过信号频带能量的变化就可以分辨出刀具故障特征。

刀具在正常和磨损两种切削状态下AE 信号各IMF 分量能量分布分别如图2 所示。从图2 可以看出，两种切削状态下AE 信号各IMF 分量能量有较大差别——正常刀具AE 信号能量集中在第1～3 阶IMF分量，而磨损刀具AE 信号能量集中第2、3 阶IMF 分量，并且第1 阶分量能量明显衰减，第3 阶分量能量明显增大。

3.2 实验结果

在刀具正常和磨损两类数据中分别随机抽取10组数据作为训练样本数据，剩下的作为测试样本数据。利用1.1 节中的特征提取方法分别提取训练和测试样本的故障特征，形成训练样本集T1和测试样本集T2。刀具状态信号能量主要集中在前几个主要的IMF 中。因此，本实验只利用前8 阶IMF 分量的归一化能量组成特征向量。

将测试样本集T2输入到该分类器中进行故障的分类。测试样本的分类结果如表3 所示。从表3 可以看出，利用FOA-GRNN 方法，刀具正常状态的分类率为100%，磨损状态分类率为90%，测试样本的总分类率达到95%。

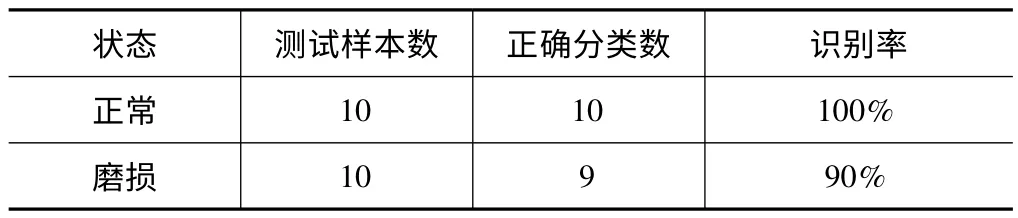
表3 FOA-GRNN 测试样本分类结果

为了进一步验证本文方法的分类性能，下面采用目前最常用的分类精度测试方法——k 折交叉确认［5］验证，对FOA -GRNN 和原GRNN 的性能进行测试。该方法的优势在于重复运用随机产生的子样本进行训练和验证，每次的结果验证1 次，10 折交叉验证是最常用的，其基本原理是将样本集随机分成10 份，轮流将其中9 份作为训练样本，1 份作为测试样本，进行分类器测试。每次测试都会得出相应的正确分类率，将10 次结果的正确分类率的平均值作为对分类器分类精度的估计。分析结果如表4 所示。

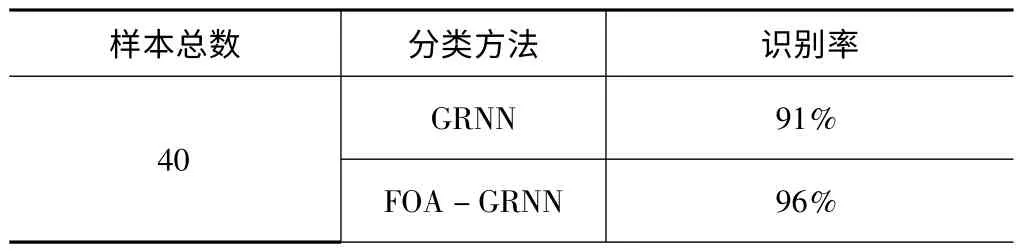
表4 10 折交叉确认验证分类结果

从表4 中可以看出，GRNN 方法的分类率为91%，利用FOA-GRNN 方法的分类率为96%，正确分类率明显提高，说明FOA -GRNN 方法的刀具状态诊断方法是有效的。

4 结语

本文实现了对刀具声发射信号IMF 分量的能量特征量提取，并利用FOA 算法优化了GRNN 的光滑因子参数，有效地区分了刀具的切削状态，提高了识别的准确率。实验证明了基于本征模函数和广义回归网络的刀具声发射信号诊断方法的有效性，通过监测AE信号IMF 能量分布，可以有效地识别刀具状态，为进一步机床刀具在线和智能检测与诊断打下基础。

［1］Tomas Kalvoda，Yean-Ren Hwang.A cutter tool monitoring in machining process using Hilbert-Huang transform［J］.International Journal of Machine Tools ＆ Manufacture，2010，50:495 -501.

［2］杨宇，于德介，程军圣，等.经验模态分解(EMD)在滚动轴承故障诊断中的应用［J］.湖南大学学报:自然科学版，2003.10(5):25-28.

［3］贾义鹏，吕庆，尚岳全.基于粒子群算法和广义回归神经网络的岩爆预测［J］.岩石力学与工程学报，2013，32(2):343 -348.

［4］Wen-Tsao Pan.A new fruit fly optimization algorithm:taking the financial distress model as an example［J］.Knowledge -Based Systems，2012，26:69 -74.

［5］周川.基于Hilbert -Huang 变换的滚动轴承故障诊断方法研究［D］.昆明:昆明理工大学，2010.