求解随机线性互补问题的光滑牛顿投影算法
单锡泉
(山东科技大学数学与系统科学学院,山东 青岛266590)
0 引言
线性互补问题(LCP)[1]定义为:寻求x∈Rn,满足
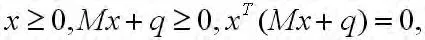
其中M∈Rn×n是一个n×n实矩阵,q∈Rn是一个n维矢量。
当我们研究实际问题时,总会受到许多不确定因素的影响,使得线性互补问题包含了不确定的数据,这就是随机线性互补问题(SLCP)[2-9]。本文研究一类特殊的随机线性互补问题,即样本空间Ω只包含有限个不确定因素ω。假设Ω={ω1,ω2,…,ωm},该问题描述为:寻求x∈Rn,满足
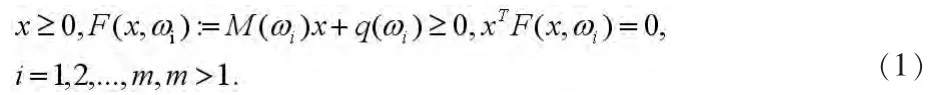
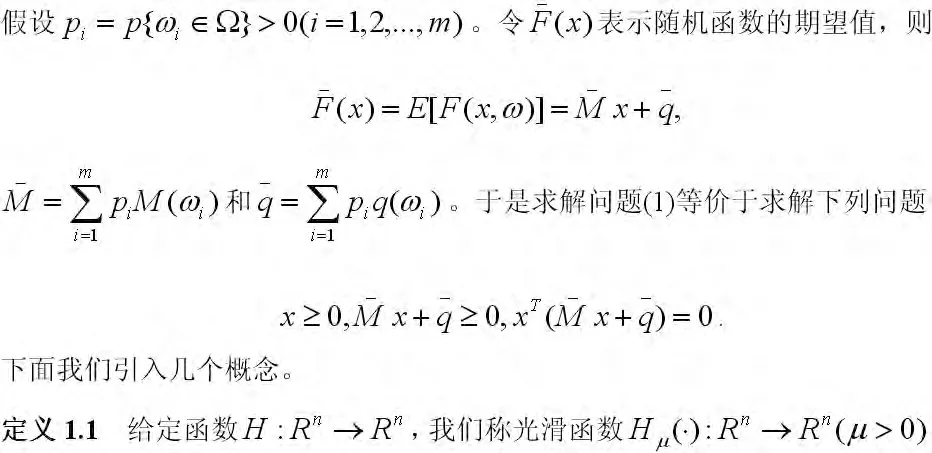
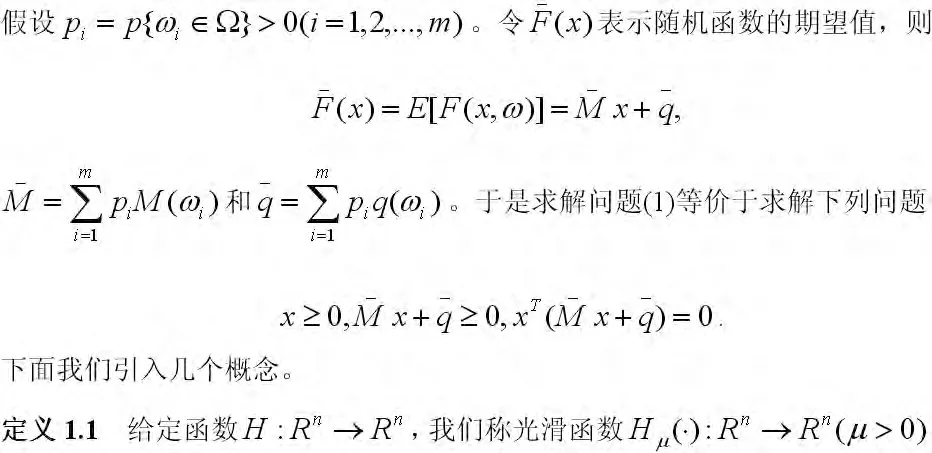
其中。于是求解问题(1)等价于求解下列问题
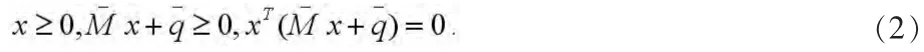
下面我们引入几个概念。

如果κ不依赖于x,则称Hμ(·)为H的一致光滑逼近函数。
定义1.2 设M∈Rn×n,若M的所有主子式皆为非负,则称M为P0矩阵。
定义1.3 函数φ∶R2→R称为NCP函数,如果它满足
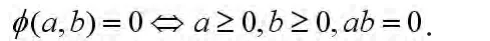
惩罚FB函数[10]

其中对任意的标量c,c+=max{0,c}是一类常见的NCP函数。下面我们构造惩罚FB函数的光滑逼近函数
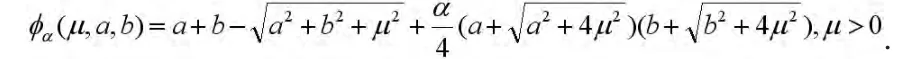
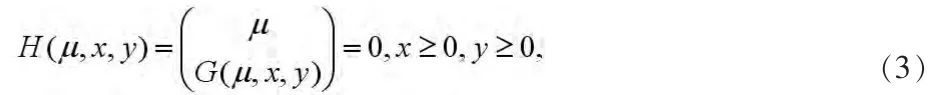
其中

因此,若问题(1)有解,问题(1)等价于问题(3)。
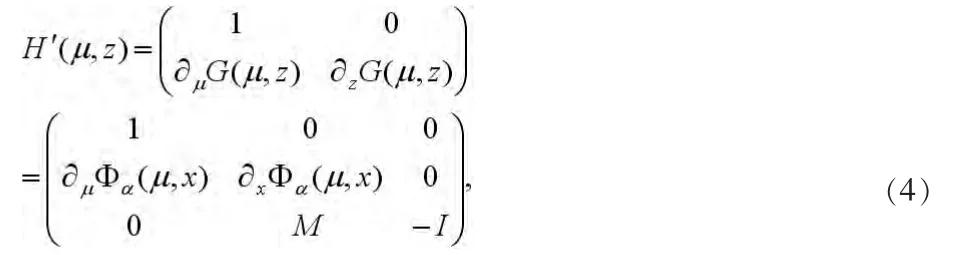
令w=(μ,z),系统(4)的价值函数可以定义为
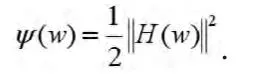
若问题(1)有解,求解系统(3)等价于寻求下列优化问题的全局解

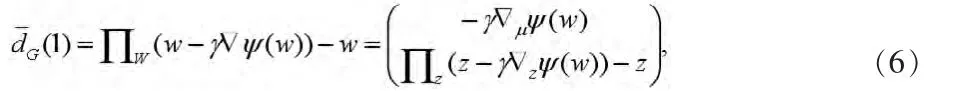
其中γ>0是一个与w有关的常数,则问题(5)的一个稳定点可以用来衡量[11]。现在基于问题(5),给出其相应的算法。
1 光滑投影牛顿算法
该算法通过运用一些扰动技术和选择恰当的搜索方向策略,保证了在相应最优化问题的任何非稳定点处光滑化变量严格为正这一关键点。对于μ>0,算法通过使用一个扰动策略,可以保证在迭代中μ>0。令α∈(0,1)为一常数,。对k=1,2,…,定义序列{βk}为
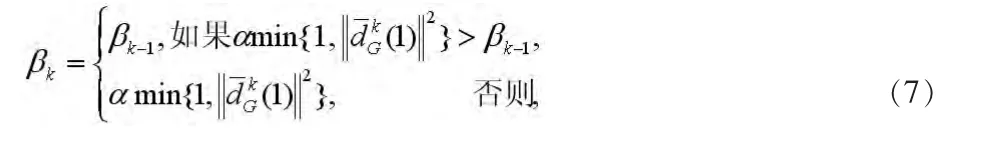
算法2.1
步1:令

步2:(计算扰动方向)

如果线性系统

有解并且有
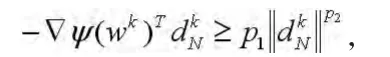
步3:(线搜索)
记满足下式的最小非负整数m为mk:
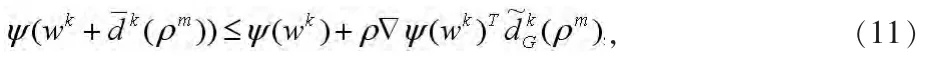
其中对任意的λ∈(0,1],
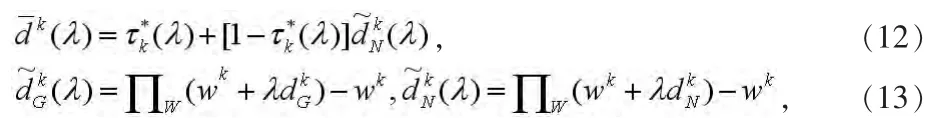
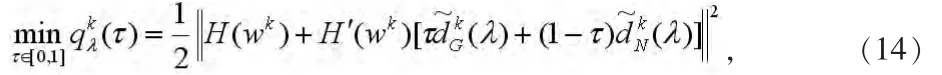
参考文[11],可得

其中

值得注意的是,因为W=R×Z,这暗示了算法中式(13)的投影计算只作用于任何点w=(μ,z)的分量z。
2 算法分析
引理3.1[12]对任意的凸集,投影算子满足
(i)对任意的w∈W,
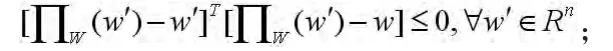
(ii)
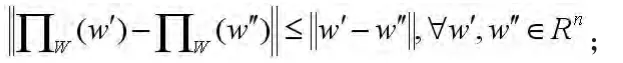

是不增的。
下面的性质显然成立。
性质3.2[13]由式(7)定义的序列{βk}有如下性质:
(i)序列{βk}是不增的;
(ii)对所有的k,βk满足
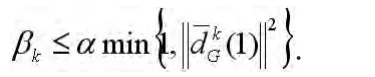
以下结果表明算法在迭代过程中能保持μ>0。

证明:该性质可以通过归纳法来证。
对k=0,由算法2.1和β0的选择可知
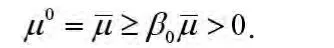
假设式(16)对k成立,接下来证明在k+l处结论依然成立。
注意到,算法中的扰动搜索方向可以看成是由两部分组成的:
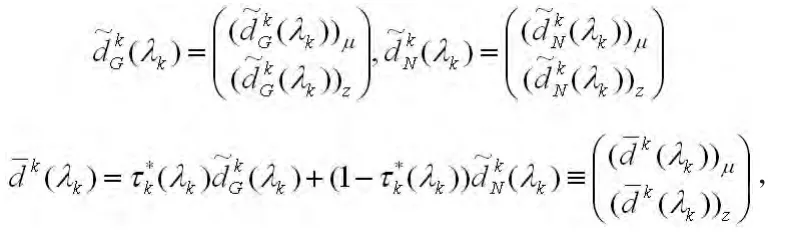
其中λk是在第k次迭代中可接受的步长。现在考虑方向针对变量μ的部分。从式(4)和(13)中,有
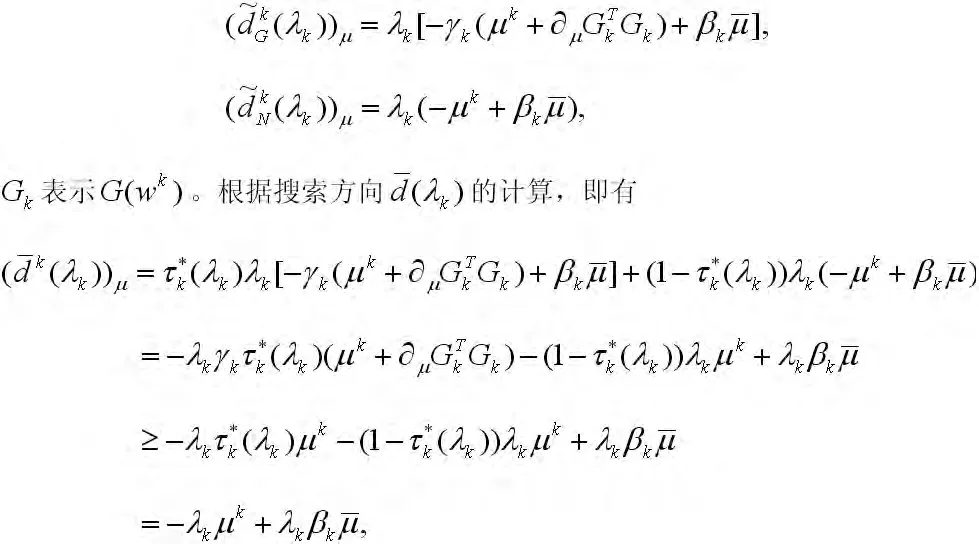
其中Gk表示G(wk)。根据搜索方向d(λk)的计算,即有
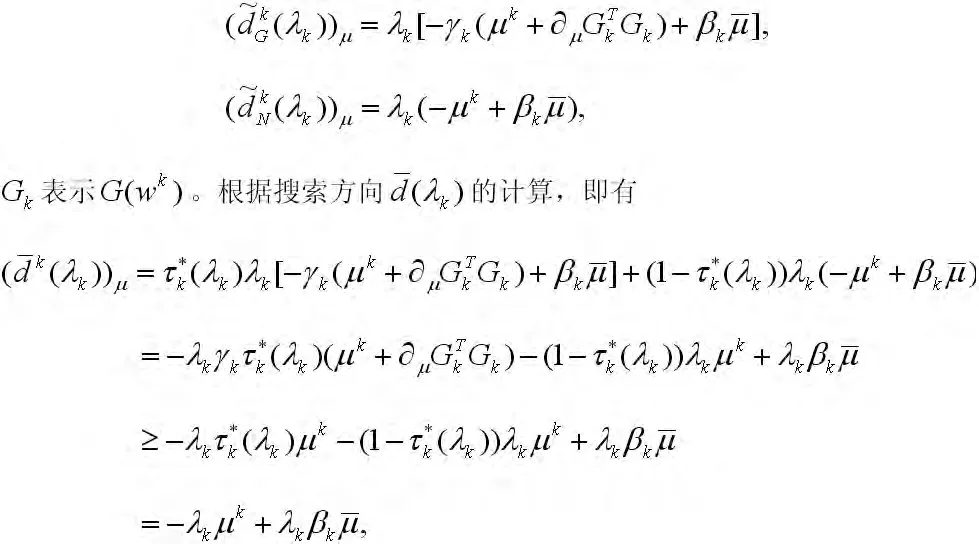
其中不等式是由γk的定义(8)得到的。从而有
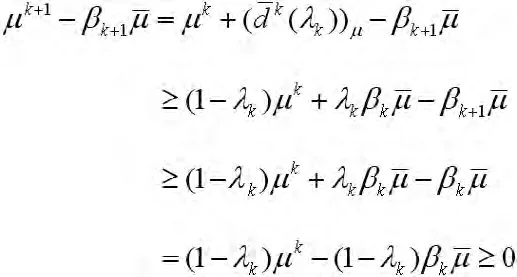
其中第二个不等式是由性质3.2中βk的单调性决定的,最后一个不等式则来自于前一点wk处的假设。因而,可以得到
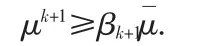
另外,如果wk和wk+1不是问题的稳定点,则由性质知βk≥βk+1>0.因此,式(16)在点wk+1处也成立,即证。
令{wk}是由算法2.1产生的迭代序列。该性质表明如果算法不在有限步内停止于一个稳定点,则对任意的k,有μk>0。这个结果暗示了由算法产生的迭代值H(w)和ψ(w)在任何点处是连续可微的。
3 算法的收敛性
定理4.1 对于算法2.1,下面的结果成立:
(i)令{wk}⊂W是由算法2.1产生的迭代序列,则{wk}的任意聚点是问题(5)的稳定点;
(ii)设w*是{wk}的一个聚点,若期望矩阵是P0矩阵,则由算法2.1得到的序列{wk}超线性收敛到w*。
证明:(i)反证法。设w˙∈W是序列{wk}的聚点,但不是问题(5)的稳定点。不妨仍以{wk}表示收敛的子列,即有,对于J acobian矩阵H′(wk),存在一常数κ2>0,使得对所有的k≥0,都有κ2。而由式子(7)和性质3.2可知,对所有的k≥0,||βk||≤α。
因此,从算法2.1的步2可得
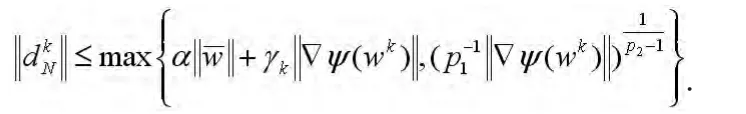
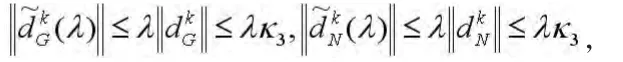
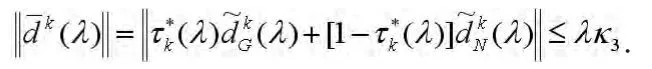
利用式(14),有
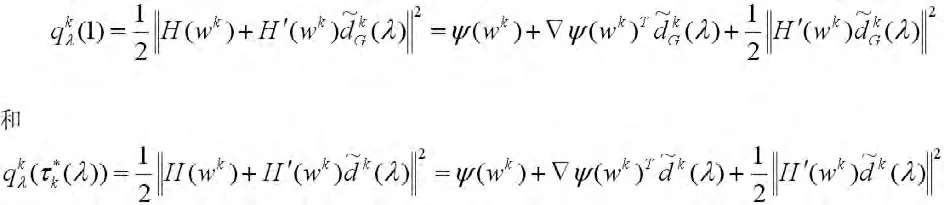
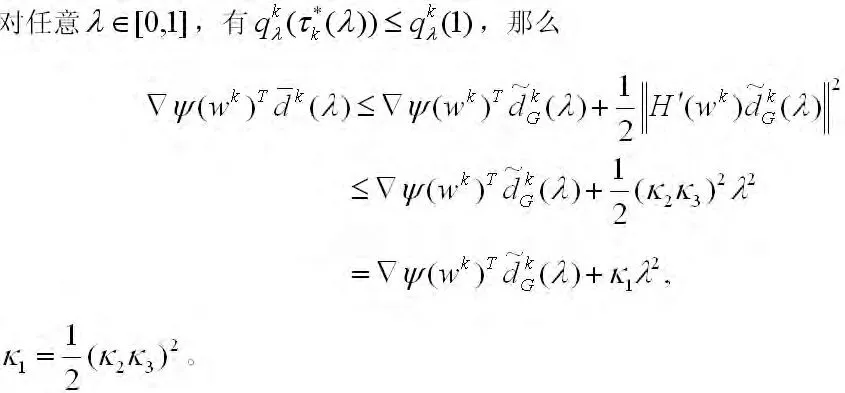
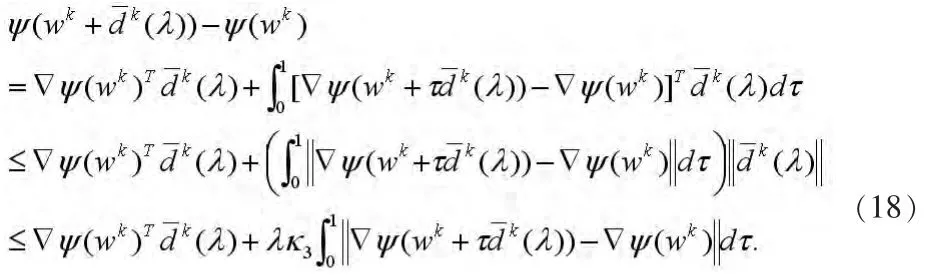
因为{wk}和对τ,λ是有界的,且在任何紧集上是一致连续的,则对任意给定的ε>0,存在一个常数,使得对所有的k≥0和λ∈[0,λ],有下列式子成立:
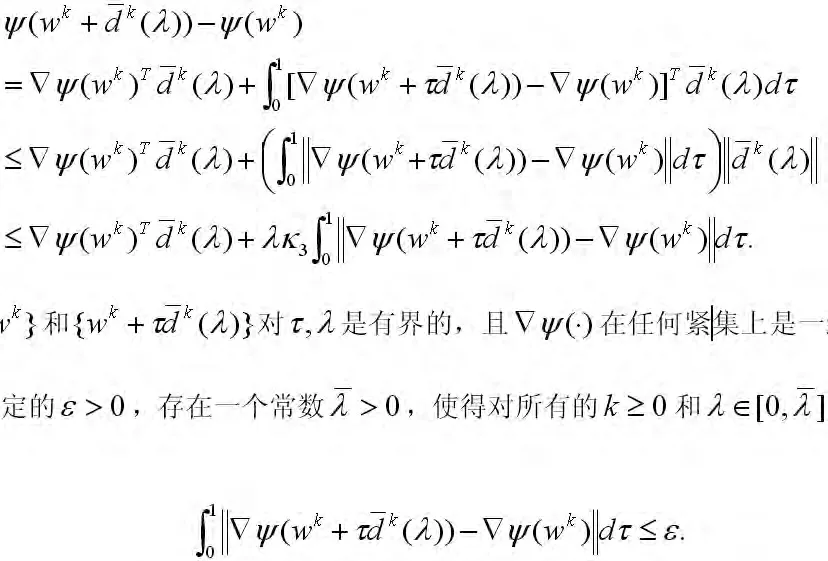
因此,从式(18)可以进一步得到,对所有的k≥0和λ∈[0,λ],
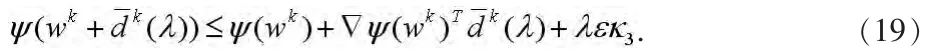
对任意的wk和λ∈(0,1],有
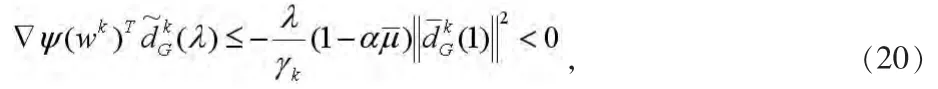
因为w˙不是问题(5)的稳定点,则存在一个常数κ4>0,使得
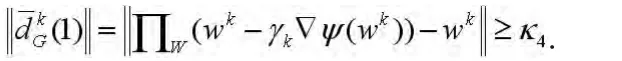
令
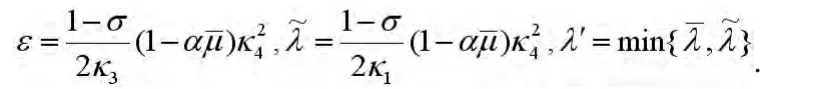
由式(17),(19)和(20)的关系以及事实γk≤1可知,对所有的k≥0和λ∈[0,λ′],有
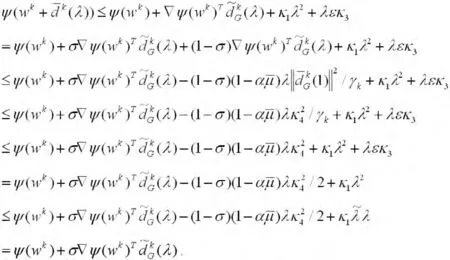
因此,由上式及算法2.1中步3所选取的线搜索可知,对所有的k≥0,有。而由不等式(11)和(20)可得,当k→∞时,有
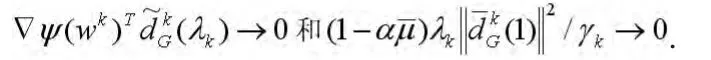
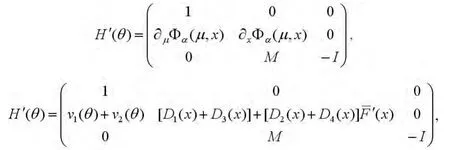
这里
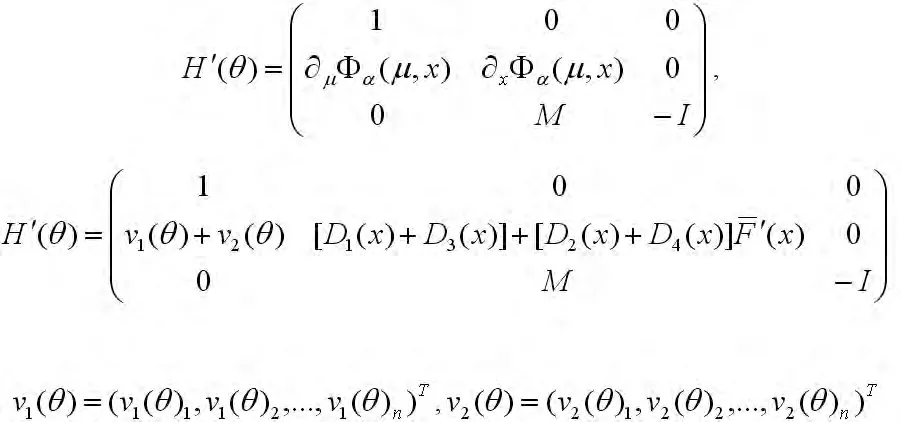
其中
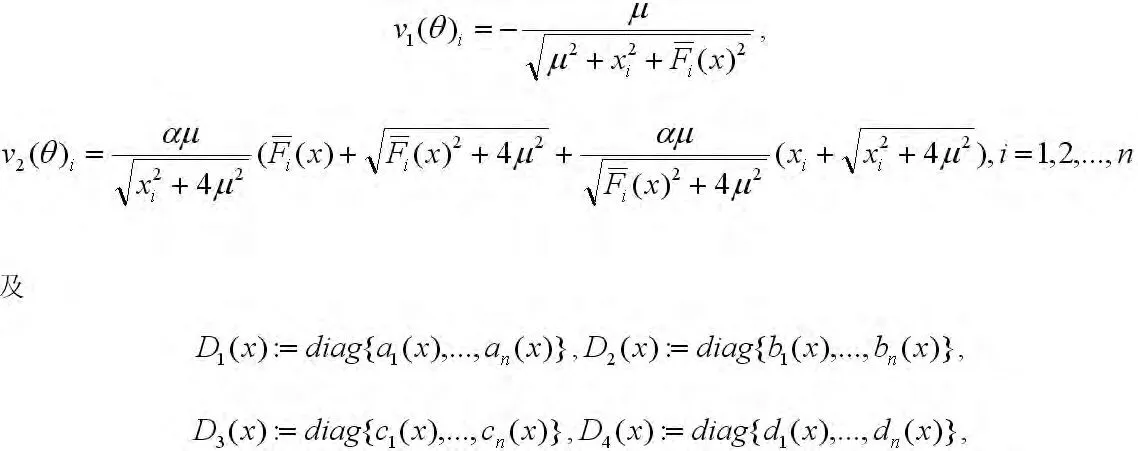
及
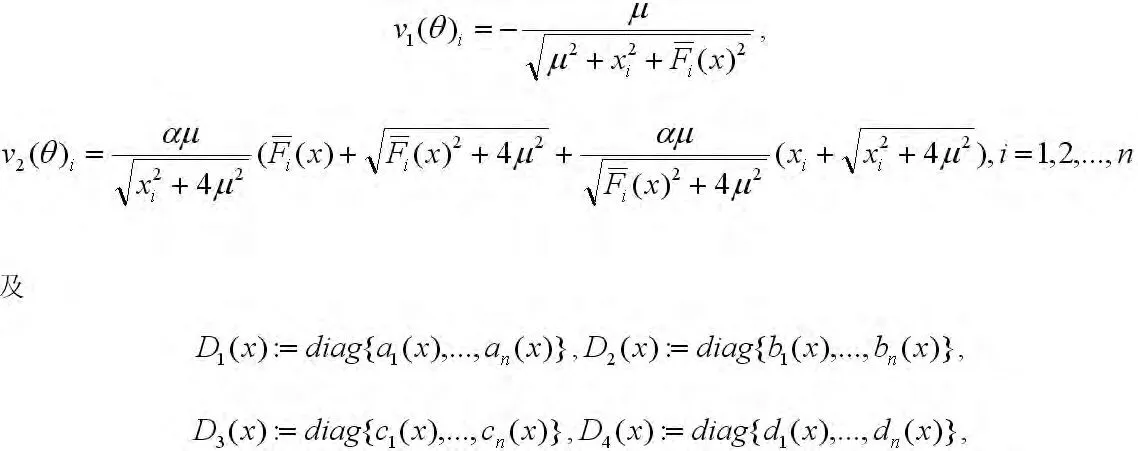
其中

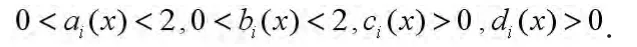
因此,对角矩阵Di(x)是正定的。另一方面,是p0矩阵,即有的所有主子式均为非负数,所以所有主子式非负,从而是正定的,因而是非奇异的。而非奇异的矩阵是BD-正则的,进而可通过文献[14]中的定理4.2相同的方法证之。
4 结束语
本文考虑了一类特殊的随机线性互补问题,通过使用光滑化的惩罚FB函数和松弛变量,将问题转化为带有非负约束的方程组,然后提出了求解这类问题的光滑投影牛顿算法,并证明了算法的全局收敛性。下一步我们将通过数值算例验证算法的有效性,并且要与已有的算法进行比较。
[1]韩继业,修乃华,戚厚铎.非线性互补理论与算法[M].上海:上海科技出版社,2006.
[2]H.F.Chen.Stochastic approximation and its applications[M].Dordrecht:Kluwer Academic Publishers,2003.
[3]X.Chen and M.Fukushima.Expected residual minimization method for stochastic linear complementarity problems[J].Mathematics of Operations Research.2005,30:1022-1038.
[4]H.Fang,X.Chen and M.Fukushima.Stochastic R0matrix linear complementarity problems[J].SIAM Journal on Optimization.2007,18:482-506.
[5]X.Chen,C.Zhang and M.Fukushima.Robust solution of monotone stochastic linear complementarity problems[J].Mathematical Programming,2009,117:51-803.
[6]G.L.Zhou and L.Caccetta.Feasible semismooth Newton method for a class of stochastic linear complementarity problems[J].Journal of Optimization Theory and Applications.2008,139:379-392.
[7]C.Zhang and X.Chen.Smoothing projected gradient method and its application to stochastic linear complementarity problems[J].SIAM Journal on Optimization.2009,20:627-649.
[8]G.H.Lin,X.Chen and M.Fukushima.New restricted NCP function and their applications to stochastic NCP and stochastic MPEC[J].Optimization.2007,56:641-753.
[9]C.Zhang and X.Chen.Stochastic nonlinear complementarity problem and applications to traffic equilibrium under uncertainty[J].Journal of Optimization Theory and Applications.2008,137:277-295.
[10]B.T.Chen,X.Chen and C.Kanzow.A penalized Fischer-Burmeister NCPfunction[J].Mathematical Programming.2000,88:211-216.
[11]D.Sun,R.S.Womersley and H.Qi.A feasible semismooth asymptotically Newton method for mixed complementary problems[J].Mathematical Programming.2002,94:167-187.
[12]P.H.Calamai and J.J.More.Projected gradient methods for linear constrained problems[J].Mathematical Programming.1987,39:93-116.
[13]杨少君.一类随机互补问题的算法研究[D].西安:西安电子科技大学,2011.
[14]X.Tong and S.Zhou.A smoothing projected Newton-type method for semismooth equations with bound constraints [J].Journal of Industrial and Management Optimization.2005,1:235-250.

