On a novel non-smooth output feedback controller for the attitude control of a small float satellite antenna
CAO Hai-qing(曹海青), WANG Yu(王渝), YAO Zhi-ying(姚志英)
(1.School of Information, Capital University of Economics and Business, Beijing 100070, China;2.School of Automation, Beijing Institute of Technology, Beijing 100081, China;2.School of Logistics, Beijing Wuzi University, Beijing 101149, China)
On a novel non-smooth output feedback controller for the attitude control of a small float satellite antenna
CAO Hai-qing(曹海青), WANG Yu(王渝)2, YAO Zhi-ying(姚志英)3
(1.School of Information, Capital University of Economics and Business, Beijing 100070, China;2.School of Automation, Beijing Institute of Technology, Beijing 100081, China;2.School of Logistics, Beijing Wuzi University, Beijing 101149, China)
A novel non-smooth controller of the second order double integrator system with a bounded disturbance is proposed, which stability is proved and which disturbance rejection capability is analyzed by MATLAB simulation experiments. The novel non-smooth output feedback controller and tracking differentiator are applied to control the azimuth servo system of the small floating satellite antenna. The MATLAB simulation and hardware in the loop simulation experiments are conducted. The experiment results validate that the non-smooth output feedback controller with stronger surge and sudden disturbance rejection capability can realize the stable azimuth servo control of the small floating antenna to ensure the communication between the target satellite and the antenna with high quality.
small floating antenna; non-smooth controller; the azimuth servo control; non-smooth output feedback controller
Non-stationary satellite antennas include vehicle satellite antenna, airborne antenna, ship-borne antenna and antenna on board[1-4]. The common characteristics of these non-stationary antennas are that the weight of the communication component set up on the carrier is lighter than the carrier’s weight. The non-stationary satellite antennas must realize the communication between the target satellite and the antenna with high quality, and ensure the antenna to point to the optimal communication zone, and stably track the target satellite. It is a key technique to completely isolate the communication influence from the motion of the carrier and quickly locate the optimal communication zone between the target satellite and the antenna. At present the PID (proportional integral derivative) control strategies have been widely applied in the process of non-stationary antenna tracking the target satellite[1-4]. But PID strategies can’t avoid the contradiction between the rapidity and overshoot of the control system since they eliminate error by error feedback in essence and the response of actuator is hysteretic. Meanwhile PID strategies are very sensitive to control gains and can’t well fit to the time-varying environment in runtime. In addition although PID strategies can well restrain the constant disturbance, they can’t well restrain nonlinear time-varying disturbances. In the paper a small floating satellite communication antenna with small volume and light weight will float within Chinese coastal waters for obscure military surveillance. A nonlinear surge disturbance will always affect the floating state of the small antenna[5]. Even the middle and small surge will seriously affect the antenna floating state and the communication quality between the antenna and target satellite since the volume of the antenna is smaller and its weight is lighter. Obviously if PID strategies are applied in the process of the attitude control of the small floating antenna, the high communication quality can’t be guaranteed since PID strategies can’t well restrain nonlinear surge disturbances in time. In the paper a new non-smooth output feedback controller will be developed to control the small floating satellite antenna attitude in the process of the antenna automatic tracking the target satellite.
1 Non-smooth feedback control
1.1 Feedback control
The feedback control is a type of control method in which the algebraic operation of the input and the output will be as a practical control quantity of the whole control system. If the output is applied to counteract the input, the feedback control is the negative feedback control which can stabilize the target system. To speed up the stable speed of the control system, the output with a certain gain will be fed back to the input of the control system. Now the linear smooth negative feedback systems have been widely applied in all kinds of the control applications. In fact the linear negative feedback control system, which convergence speed variation near the equilibrium point is an exponential function, is an asymptotically stable system. The linear negative feedback system easily leads to some discontinuous phenomenon for example nonlinear flutter and doesn’t well restrain all kinds of disturbance[6]. For the attitude control of a small floating antenna system the linear feedback control is not the best control method since the linear feedback control can’t well and completely restrain the varying sudden disturbance and varying surge disturbance.
The non-smooth control method is a nonlinear control method between the smooth control method and the discontinuous control method[6-8]. The non-smooth feedback control will feed back the output of the non-smooth controller to the input of the target system and calculate their algebraic operation results as the practical control quality to control the target system. The non-smooth control can make the target system quickly converge to the equilibrium point in a finite time and well restrain the disturbance in time. For a non-smooth feedback control system it is difficult to design a reasonable non-smooth controller.
1.2 A new non-smooth controller
The double integrator system can easily be extended to the general second order system[7], so the standard controllable double integrator system is considered as the research object of a new non-smooth controller. Consider the system
(1)
whered(t) is a bounded disturbance, 0≤d(t)≤l,uis the input,yis the output. Now the global finite-time non-smooth controller of the double integrator system without a disturbance
u=-k1|x1|α1sgn(x1)-k2|x2|α2sgn(x2)
(2)

(3)
isstudiedinRef.[10]onthebaseoftheLyapunovtheory.Thecontroller(3)willmakethedoubleintegratorsystemconvergetothezoneQin a finite time.
Q=

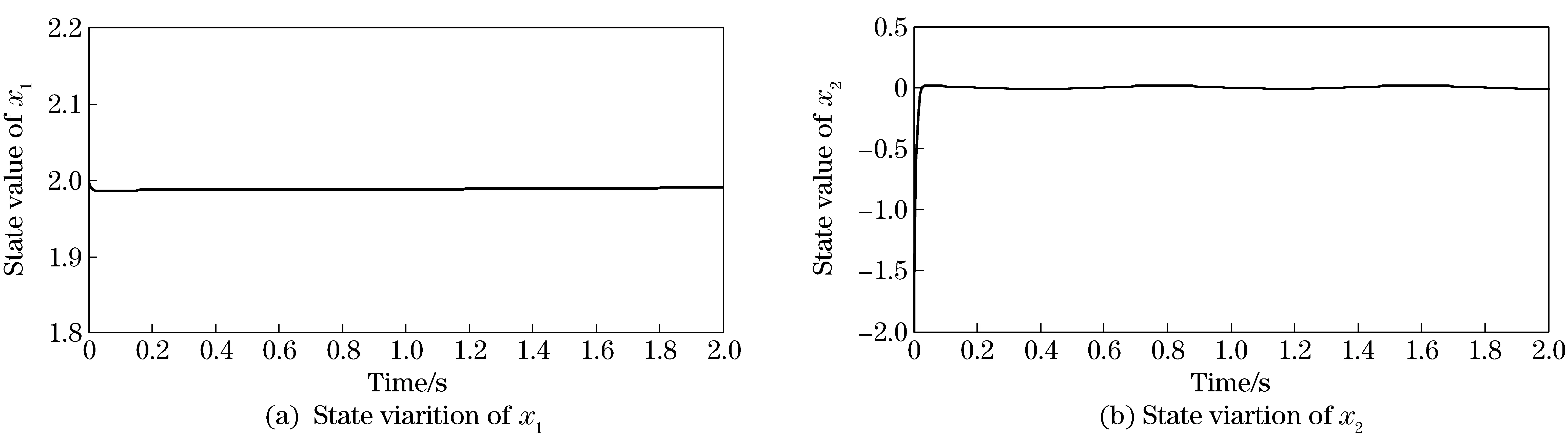
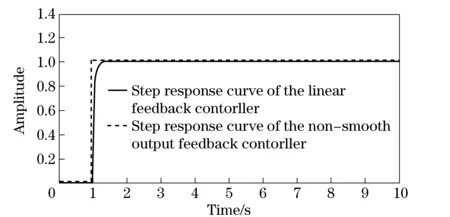
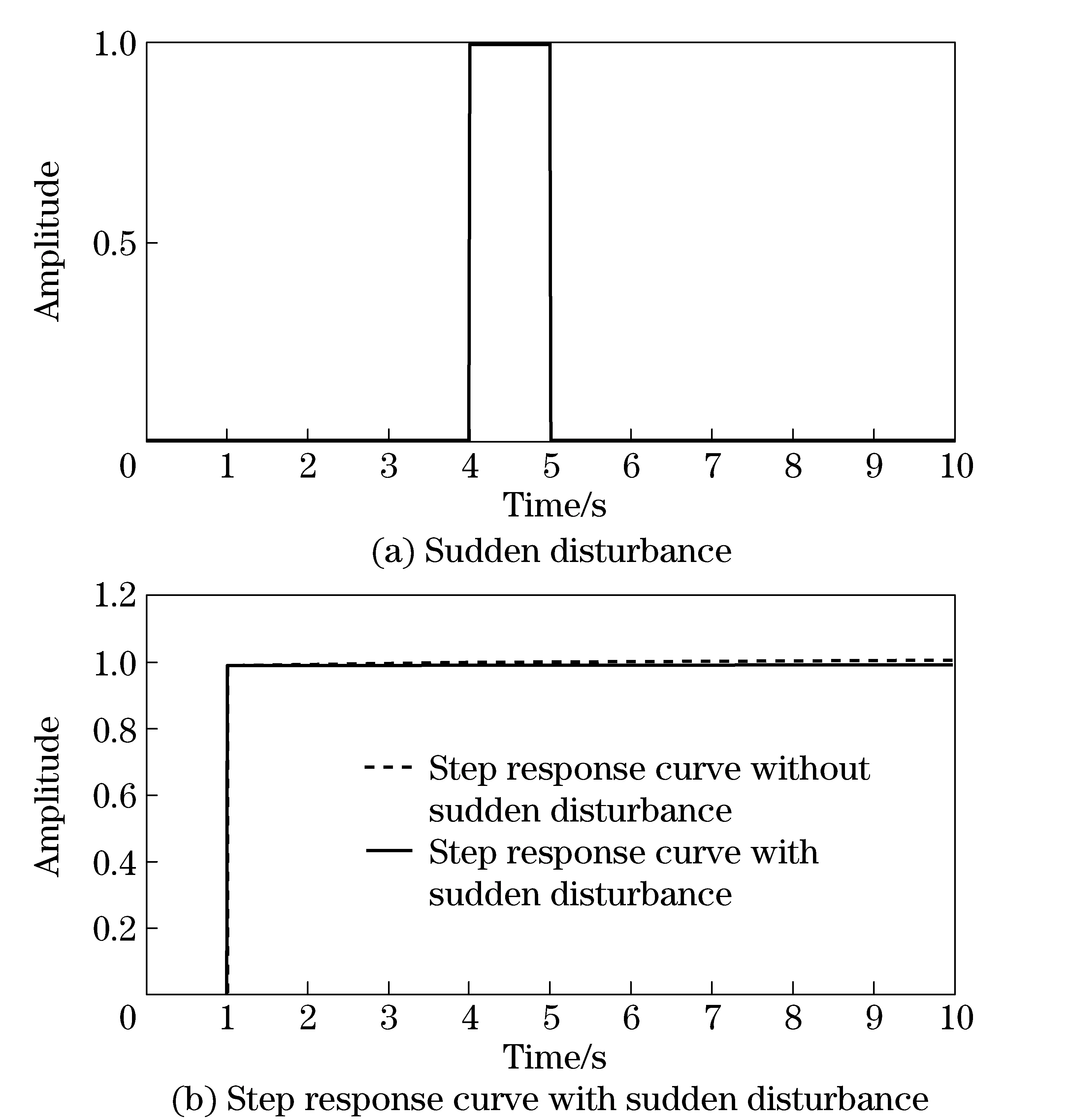
wherek1>0, 1 0 Obviously the above mentioned non-smooth controller of the double integrator with a bounded disturbance is quite complex. The non-smooth controller of the double integrator has non-uniqueness[11], so in the paper a new simple non-smooth controller of the double integrator with a bounded disturbance (4) whichisastablefinitetimenon-smoothcontroller,isproposed,wherek1>0,k2>0,0<2α1+1<1,and2α1+1=n/m, misaodd, mandnarecomprisenumbers, 0<α2<1. Proof Consider a Lyapunov function candidate for system (1): x1∈R,x2∈R (5) wherecis a constant andc>0. ObviouslyV(x1,x2) is a continuously differentiable function defined onR, positive definite and radially unbounded sincec>0 and 2α1+1>0.ThederivativeofV(x1,x2)is (6) AaccordingtoEqs. (1) (4),Eq.(1)canbechangedto (7) AccordingtoEqs. (6) (7),Eq.(6)canbechangedto k2x2|x2|α2sgn(x2)+x2d(t) (8) Letc=k1,then x2d(t)≤-k2|x2|α2+1+|x2|d(t) (9) So if and only if -k2|x2|α2+1+|x2|d(t)≤0,thecontroller(4)isstableinafinitetime z=u+d(t), 0 (10) Obviously the system (10) is a standard one order integrator system with a bounded disturbanced(t). Let us design a non-smooth controller u=-k|z|αsgn(z) (11) for the standard one order integrator system. In order to prove the non-smooth controller (11) is stable, consider another Lyapunov function (12) ObviouslyV1(z) is a continuously differentiable function defined onR, positive definite and radially unbounded. V1(z)≥0 (13) The derivative ofV1(z) is -k|z|α+1+l1|z|=(-k|z|α+l1)|z| (14) Now let us refer to the theorem from Refs.[7,12]. (-k|z|α+l1)|z|≤-c≤0 (15) Soitisnodoubtthatthenon-smoothcontroller(4)ofthedoubleintegratorisafinitetimestablenon-smoothcontrolleraccordingtotheLyapunovtheory. 1.3 Capability of the disturbance rejection on the novel non-smooth controller The attitude control of a small floating satellite antenna under the medium and small surge is studied in the paper. A surge will be looked on as a surge disturbance when its angular frequency exceeds the frequency bands of the medium and small surge. The surge disturbance will seriously affect the attitude control. In additional a sudden disturbance caused by some floating bodies near the float antenna will also affect the attitude control of the antenna. To validate the disturbance rejection capability of non-smooth controller, the disturbance rejection capability for the surge disturbance and sudden disturbance are respectively inspected by MATLAB numerical simulation. Fig.1 Disturbance rejection of the surge (17) ①Surge disturbance rejection The parameters of the medium and small surge are listed as follows[5]: the significant wave heighth1/3is not larger than 2 m, the wind speed is less than 9.7 m/s, the wave length is less than 60 m, the cycle is less than 6.1 s, the angular speed ranges between 0.3 rad/s and 3 rad/s. The surge can be expressed by the plate wave y=h1/3cos (ωt+φ) (16) whereh1/3is the significant wave height, ωistheangularfrequency, φistheinitialphase.Supposeadisturbancecanbeexpressedby d(t)=0.2cos (4t)≤0.2 (17) The initial state of the double integrator system (1) is ((x1,x2))=(2,-2), the parameters of the non-smooth controller (4) arek1=150,k2=0.5, 2α1+1=10/11, α2=0.1,thestateofthedoubleintegratorsystemwillquicklystabilizeto((x1,x2))=(2,0)inlessthan0.05sunderthesurgedisturbance(17)whichisshowninFig.1.Obviouslythenon-smoothcontrollerhasastrongersurgedisturbancerejectioncapability.Inordertovalidatethesurgedisturbancerejectionrobustness,anothersurgedisturbancecanbeexpressedby d(t)=3cos (8t)≤3 (18) The parameters of the non-smooth controller (4) are invariable. The state of the double integrator system will quickly stabilize to ((x1,x2))=(2,0) in less than 0.05 s under the surge disturbance (18) which is shown in Fig.2.So the non-smooth controller (4) has strong robustness for the surge disturbance and can well restrain the surge disturbance in time. ② Sudden disturbance rejection The small floating satellite antenna will float within some sea area; it will often suppress some sudden disturbances from ships and marine organism near it. These disturbances can be expressed by a pulse signal with a short cycle and constant amplitude. The double integrator system (1) starts with its initial status ((x1,x2))=(2,-2), and a sudden disturbance expressed by (19) isinputtothesystem.Thelaststateofthesystemwillconvergeto((x1,x2))=(2,0). The process of the variation of the system state is shown in Fig.3. Fig.2 Disturbance rejection of the surge(18) Fig.3 System state under the sudden disturbance Obviously the non-smooth controller (4) can well restrain the sudden disturbance and the control system will quickly converge to the stable state in a finite time. Meanwhile the non-smooth controller (4) has strong robustness to reject the sudden disturbance. 2.1 Structure of the non-smooth output feedback controller of the small floating satellite antenna attitude control The attitude control of the small floating antenna is realized by three-axis servo actuator motion to compensate for the deviation between the antenna direction and the idea communication zone caused by the surge. The azimuth servo system controls the azimuth actuator to compensate the deviation of the azimuth; the elevation servo system controls the elevation actuator to compensate the deviation of the elevation; the polarization servo system controls the polarization actuator to compensate the deviation of the polarization. The deviation of the roll angle caused by the surges will be compensated by the azimuth servo system, the elevation servo system and the polarization servo system by decoupling method. The azimuth servo system, the elevation servo system and the polarization servo system belong to the second order system. In the paper the non-smooth controller in section 1.2 will be applied to realize the azimuth attitude control of the small floating antenna. The azimuth non-smooth output feedback controller structure of the small floating antenna is shown in Fig.4. 2.2 Non-smooth output feedback controller The non-smooth output feedback controller expressed by (20) (21) Fig.4 Structure of the non-smooth output feedback controller of the small floating antenna Fig.5 Sine signal and its differentiator Fig.6 Step signal and its differentiator 2.3 Motor and motor driver of the azimuth servo system The permanent magnet DC motor will be applied in the azimuth servo control system of the small float antenna. The transfer function of the motor can be simplified as[13] (22) wherekmis the moment coefficient of the motor,Rais the resistance of the armature circuit,Lais the inductance of the armature circuit,Jis the moment of inertia including the motor and the load,kεisthebackEMF(electromotiveforce)coefficient.WhenLsisverysmall,thetransferfunctionofthemotorcanbeapproximatelysimplifiedas: (23) whereTmis the electromechanical constant of the motor which can be expressed by Tm=RaJ/(kekm),K=1/kε (24) By reference to the motor manual and considering the actual environment, the transfer function of the motor can finally be expressed by (25) Themodelofthemotordrivercanbesimplifiedasaone-orderinertiallink Gc=kc/(Tcs+1) (26) by reference of the motor manual. The parameterkcis equal to 0.6 andTcis equal to 0.3 by fitting the step response curve of the motor driver. Thus the transfer function of the motor driver can be expressed by Gc=0.6/(0.3s+1) (27) So the control model of the motor can be expressed by G(s)=Gc(s)Gm(s)= (28) Obviouslythemotorcontrolsystemisasecondordersystem. The control effect of the non-smooth output feedback controller of the small floating antenna is investigated by MATLAB simulation and hardware in the loop simulation. 3.1 MATLAB simulation of the non-smooth output feedback controller Firstly the comparison of the step response of the non-smooth output feedback controller withk1=150,k2=0.5, 2α1+1=10/11,α2=0.1andlinearfeedbackcontrollerisshowninFig.7byinputtingastepsignaltothenon-smootheroutputfeedbacksystemandthelinearfeedbacksystemrespectively.Obviouslytheresponseofthenon-smoothoutputfeedbackcontrollerwithzeroovershotisquickerthanthatofthelinearfeedbackcontroller.Thenasurgedisturbancesignalexpressedby (29) isaddedtothestepsignaltoinputthesystemandtheresultisshowninFig.8. Obviouslythenon-smoothoutputcontrollercanwellandquicklyrestrainthesurgedisturbance.AtlastaunitpulsesignalasasuddendisturbanceshowninFig.9isaddedtotheinput,theresponsecurveofthenon-smoothoutputfeedbackcontrollerisshowninFig.9.FromFig.9itisclearthatthenon-smoothoutputfeedbackcontrollercanwellrestrainthesuddendisturbanceandhasstrongrobustnesssincethemaximumabsoluteerrorbetweenthestepresponsecurvewithasuddendisturbanceandthestepresponsecurvewithoutasuddendisturbanceis0.004anditcanbeignored. Fig.7 Comparison of the step response of the non-smooth output feedback controller and the linear feedback controller Fig.8 Step response curves with surge disturbance 3.2 Hardware in the loop simulation of the non-smooth output feedback controller The small float satellite antenna is put on the six degree of freedom swaying platform, and the platform is put on the flat car. The hydrostatic flow is simulated by the translation of the flat car and the surge disturbance is simulated by the swing of the swaying platform. The above hardware in the loop simulation is conducted in the condition of the small antenna floating on sea to validate the control effect of the non-smooth output feedback controller with the parametersk1=150,k2=0.5, 2α1+1=10/11, α2=0.1.FirstlythesmallfloatantennalocatedtheChinasat10satellite,thentheflatcarstartedtranslationatthespeedof2m/sandthesixdegreefreedomplatformswayedatthetrailξ≈2cos(t),intheprocessofexperimenttheelectromagneticacquisitioncomponentacquiredtheAGC(autogaincontrol)foranhour.ThecurveoftheAGCacquiredisshowninFig.10.IthasbeenvalidatedthatthesmallfloatantennacancommunicatewiththetargetsatellitewithhighqualitysincetheamplitudeoftheAGCisoninterval[248, 265].Itisprovedthatthenon-smoothoutputfeedbackcontrollerofthesmallfloatantennacanwellrealizetheantennastabletrackingthetargetsatelliteandensurethecommunicationbetweentheantennaandthetargetsatellitewithhighquality. Fig.9 Step response curve with sudden disturbance Fig.10 AGC value in the process of testing Anovelnon-smoothcontrollerisproposedforthestandarddoubleintegratorsystemwithaboundeddisturbance.Thenstabilityofthenon-smoothcontrollerisprovedbyLyapunovtheory.Thecapabilityofthedisturbancerejectionofthenon-smoothcontrolleronthesurgedisturbanceandthesuddendisturbanceisvalidatedbyMATLABsimulations.Itisprovedthatthenon-smoothcontrollerhasastrongerabilityandstrongrobustnesstorestrainallkindsofdisturbances. Thenon-smoothoutputfeedbackcontrollerfortheazimuthservosystemofthesmallfloatantennaisdesignedfortheazimuthservoactuator.Theoutputoftheazimuthservosystemanditsderivativecalculatedbythetrackingdifferentiatorareinputtothenon-smoothoutputfeedbackcontroller,andtheoutputofthenon-smoothoutputfeedbackcontrollerisfedbacktotheinputoftheazimuthservocontrolsystemtocontroltheazimuthattitudeofthesmallfloatantenna.TheMATALBsimulationandthehardwareintheloopsimulationexperimentsareconducted.Resultsvalidatethatthenon-smoothoutputfeedbackcontrollerisbetterthanthelinearnegativefeedbackcontroller,andhasastrongabilityandrobustnesstorestrainthesurgedisturbanceandsuddendisturbance.Thenon-smoothoutputfeedbackcontrollerofthesmallfloatantennacanwellrealizethecommunicationbetweentheantennaandthetargetsatellitewithhighquality. [1] Omihiko Y, Kohei O, Masazumi U. Highly accurate and cost-effective auto-tracking antenna system for satellite broadband communication on vessels[J].NTT Technical Review,2005,9(3):60-71. [2] Hee V S D. Airborne satellite antenna mount and tracking system[C]∥7th African Conference in Africu, Gaborone, 2004: 289-295. DOI: 10.1109/AFRICON.2004.1406676. [3] Tao K Y, Jin Y W, Yan Y M. Control algorithm for servo tracking system of carrier-based satellite antenna[J]. Ordnance Industry Automation.2006,25(8):55-58. (in Chinese) [4] Cao Haiqing, Wang Yu, Yao Zhiying. Optimization of satellite searching strategy of the non-stationary antenna[J]. Journal of Beijing Institute of Technology, 2015, 24(3):398-404. [5] Zhun J. Ship statics[M]. Changsha: National Defense Science and Technology University Press, 2002. (in Chinese) [6] Hong Y, Huang J,Xu Y S. On an output feedback finite-time stabilization problem[J]. IEEE Transactions on Automatic Control,2001,46(2):305-308. [7] Bhat S P, Bernstein D S. Finite-time stability of homogeneous systems[C]∥Proceedings of the American Control Conference,1997:1073-1078. [8] Bhat S P, Bernstein D S. Continuous finite-time stabilization of the translational and rotational double integrators[J]. IEEE Transactions on Automatic Control,1998,43(5): 678-682. [9] Ding S H,Li S H,Li Q. Stability analysis for a second order continuous finite-time control system subject to a disturbance [J]. J Control Theory Application, 2009,7(3):271-276. [10] Hong Y, Huang J,Xu Y S. On an output feedback finite-time stabilization problem[J]. IEEE Transactions on Automatic Control,2001,46(2):305-308. [11] Emmanuel B, Wilfrid P, Denis E, et al.Finite-time output stabilization of the double integrator[C]∥51st IEEE Conference on Decision and Control,2012:5906-5911. [12] Li S H, Ding S H, Dou H B,et al.Non-smooth control theory and application[M]. Beijing:Science Press, 2013. (in Chinese) [13] Liu Y, Zhang K, Li Y J. Modeling and simulation research of control system of random position[J]. Journal of Projectiles Rockets,Missiles and Guidance,2005,25(2):2-4. (in Chinese) (Edited by Wang Yuxia) 10.15918/j.jbit1004-0579.201524.0320 TP 272 Document code: A Article ID: 1004- 0579(2015)03- 0413- 09 Received 2014- 01- 21 Supported by Academic Innovation Project of Beijing(201106149) E-mail: cxy8888@bit.edu.cn


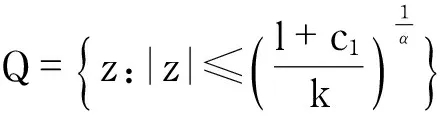

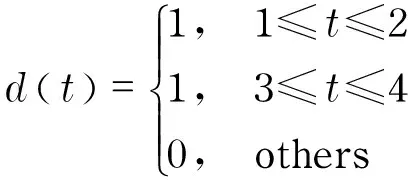


2 Non-smooth controller of the small floating satellite antenna attitude control

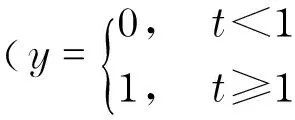
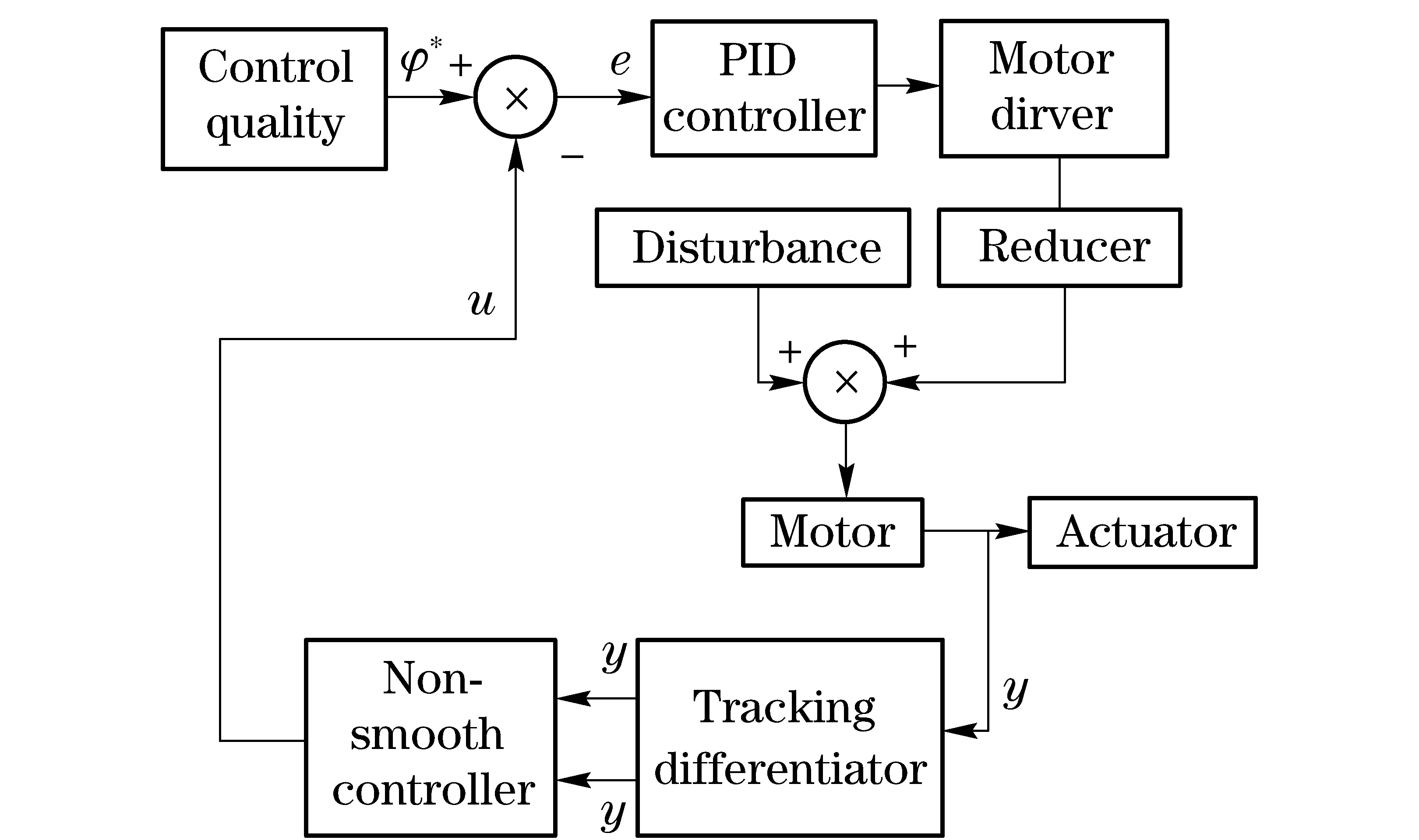


3 Numerical simulation of the non-smooth output feedback controller of the small floating antenna
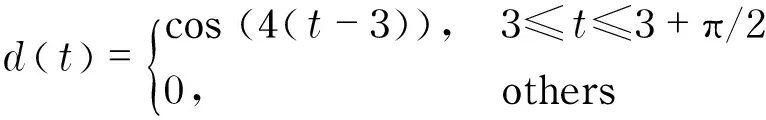


4 Conclusion
 Journal of Beijing Institute of Technology2015年3期
Journal of Beijing Institute of Technology2015年3期
