Joint receiving mechanism based on blind equalization with variable step size for M-QAM modulation

LU Ji-hua(卢继华), Abdallah Elhirtsia AHMED, WANG Xiao-hua(王晓华),Kheddar BOUDJEMAA

(1.School of Information and Electronics, Beijing Institute of Technology, Beijing 100081, China.2.School of Mechatronic Engineering, Beijing Institute of Technology, Beijing 100081, China)



Joint receiving mechanism based on blind equalization with variable step size for M-QAM modulation

LU Ji-hua(卢继华)1, Abdallah Elhirtsia AHMED1, WANG Xiao-hua(王晓华)1,Kheddar BOUDJEMAA2

(1.School of Information and Electronics, Beijing Institute of Technology, Beijing 100081, China.2.School of Mechatronic Engineering, Beijing Institute of Technology, Beijing 100081, China)

The problem of inter symbol interference (ISI) in wireless communication systems caused by multipath propagation when using high order modulation like M-QAM is solved. Since the wireless receiver doesn’t require a training sequence, a blind equalization channel is implemented in the receiver to increase the throughput of the system. To improve the performances of both the blind equalizer and the system, a joint receiving mechanism including variable step size (VSS) modified constant modulus algorithms (MCMA) and modified decision directed modulus algorithms (MDDMA) is proposed to ameliorate the convergence speed and mean square error (MSE) performance and combat the phase error when using high order QAM modulation. The VSS scheme is based on the selection of step size according to the distance between the output of the equalizer and the desired output in the constellation plane. Analysis and simulations show that the performance of the proposed VSS-MCMA-MDDMA mechanism is better than that of algorithms with a fixed step size. In addition, the MCMA-MDDMA with VSS can perform the phase recovery by itself.

inter symbol interference (ISI); modified constant modulus algorithm (MCMA); modified decision directed modulus algorithm (MDDMA); variable step size; blind equalization; phase rotation

Inter symbol interference (ISI) caused by limited bandwidth, multipath and a change with time of the wireless channels for home networking has been known as a major problem for high speed data transmission. Hence, it is necessary to use an adaptive equalizer which is a linear time varying filter that gives an estimation inverse of the channel[1]to track the channel variation and reduce the ISI effects. The adaptive equalizer used in wireless receiver needs some algorithms such as the least mean square (LMS) and recursive least square (RLS) algorithms[2-3]. Whereas, these algorithms based on the attachment of training sequence with the transmitted information for learning the channel decreases the bandwidth efficiency of the system[4].

On the other hand, the blind equalization technique uses statistical properties of the transmitted signal instead of the training sequence thus increases the throughput of the system. The blind equalization technique includes algorithms such as the constant modulus algorithm (CMA)[4].

The CMA works well for modulations with a circular constellation, such as the M-ary phase shift keying (PSK) modulation. However, for M-ary QAM modulation when the constellation is composed of a square lattice of signal points, the CMA doesn’t performance well and may obtain a convergence with phase error. In order to improve the performance of the CMA with M-QAM signals, enhanced algorithms are proposed in Refs.[5-9]. Particularly, the modified constant modulus algorithm (MCMA) proposed in Ref.[5] is designed to solve the problem of phase rotation in high order QAM signals. Inspired by the CMA blind equalization scheme for M-QAM modulated signals, the decision directed modulus algorithm (DDMA) was developed[10]. Furthermore, the MDDMA proposed in Ref.[11] incorporates the advantages of MCMA and DDMA. The dual cost function of the combined MCMA and MDDMA in Refs.[11-12] are formulated to improve the performances for M-QAM modulation, which are referred as the MCMA-MDDMA algorithms here.

The convergence rate and the mean square error (MSE) are used to measure the performances of blind equalization algorithms. For example in wireless home network, the convergence rate shows how long the service will be blocked on the network when the channel’s characteristics changes. The MSE has relation to the quality of service and the throughput of the system. The step size factor has an important influence when evaluating the convergence rate and MSE, and hence, it is directly related to the blind equalization algorithm’s performance[13-14].

1 Block of a wireless communication system with proposed algorithms

1.1 Wireless communication system with an adaptive blind equalizer

Fig.1 shows a simple wireless communication system model with an adaptive blind equalizer.

The received signalx(k) and the output of equalizery(k) in Fig.1 can be expressed as

(1)

y(k)=W(k)*X(k)

(2)

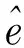
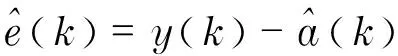
(3)

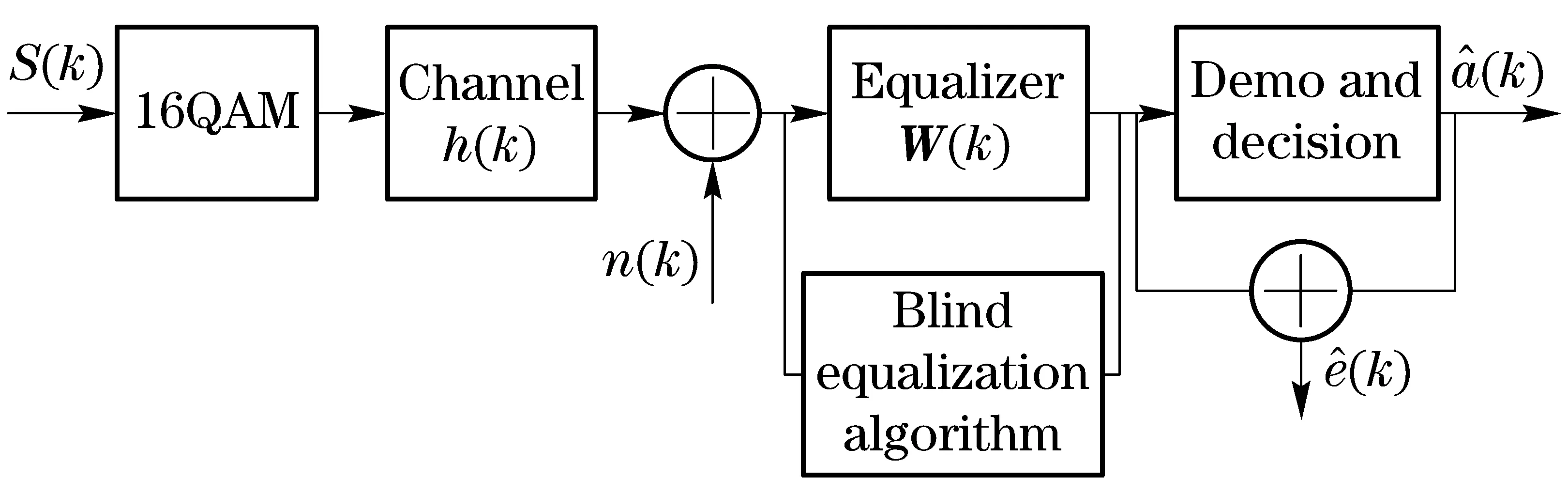
Fig.1 Block diagram of a wireless communication system with an adaptive blind egualizer

1.2 MCMA

The cost function of MCMA proposed in Ref.[5] is given by the decomposition of CMA cost function[4]with real and imaginary parts. This will use the information of both phase and amplitude at the equalizer output in order to solve the existing problem of phase rotation in M-QAM signals. However, this cannot be solved by the cost function defined in the CMA, the cost function of which is written as

JCMA(k)=E[(|y(k)|2-D)2]

(4)

whereE[·] denotes the statistical expectation andDis a constant determined by the statistics of transmitted informationa(k), expressed as

(5)

InsteadofCMA,theMCMAcostfunction[5]isgivenbythesumofrealandimaginarycostfunctionsJR(k) andJI(k), respectively. These two components are formulated as

JR(k)=E[(|yR(k)|2-DR)2]

(6)

JI(k)=E[(|yI(k)|2-DI)2]

(7)

wherey(k)=yR(k)+jyI(k) and the constantsDRandDIare defined as

(8)

wherea(k)=aR(k)+jaI(k).

Using the gradient descendent method, the updated tap weight vectorw(k+1) in the MCMA is expressed as

w(k+1)=w(k)-μeMC(k)X*(k)

(9)

whereμis the step size factor ;eMCis the estimated error of MCMA algorithm and

eMC(k)=eR(k)+jeI(k)

(10)

eR(k)=yR(k)(|yR(k)|2-DR)

(11)

eI(k)=yI(k)(|yI(k)|2-DI)

(12)

1.3 MDDMA

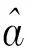
(13)

UsingthesameideawhenmodifyingtheCMAcostfunctiontocreatetheMCMA,theMDDMA[11]dividestheDDMAcostfunction[10]intorealandimaginaryparts,respectivelyas

(14)

(15)

TheupdatedcoefficientofMDDMAisgivenby

w(k+1)=w(k)-μeMD(k)X*(k)

(16)

whereeMD(k)=eMR(k)+jeMI(k) is the error function, and its and imaginary parts are

(17)

(18)

1.4CombinedMCMA-MDDMA

MCMA-MDDMAisproposedbyusingacombinedcostfunctionofbothMCMAandMDDMA[11].ThisalgorithmhasshownagoodperformancewhencomparedwithMCMA[12].Keepingthesamenotationscitedpreviously,thecostfunctionofMCMA-MDDMAis

JMM(k)=JMMR(k)+JMMI(k)

(19)

with

JMMR(k)=E[(|yR(k)|2-DR)2]+

(20)

JMMI(k)=E[(|yI(k)|2-DI)2]+

(21)

TheupdatedcoefficientofMCMA-MDDMAcanbedescribedas

w(k+1)=w(k)-μeMM(k)X*(k)

(22)

where

eMM(k)=eMMR(k)+jeMMI(k)

(23)

The real and the imaginary parts ofeMM(k) are respectively expressed as

eMMR=yR(k)(|yR(k)|2-DR)+

(24)

eMMI=yI(k)(|yI(k)|2-DI)+

(25)

2 Proposed VSS receiving scheme

2.1 Convergence of MCMA-MDDMA with fixed step size

Fig.2 MSE convergence curves for MCMA-MDDMA with a fixed step size

The inefficiency of using a fixed step size is simulated under the following conditions: Input of information is a 16-QAM modulated signal and the channel impulse vector ish1=10.129 4+0.483j. An AWGN is added to the input with signal-to-noise ratio (SNR) of 35 dB. Fig.2 illustrates the convergence curve of MCMA-MDDMA with different values of fixed step size. Results show that MCMA-MDDMA with a fixed step size suffers from a compromise between the convergence rate and the convergence steady state MSE.

2.2 Proposed MCMA-MDDMA with VSS

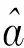
Fig.3 Two states of MCMA-MDDMA with fixed step size

In this section, a VSS is proposed. Then, it is applied to combined MCMA-MDDMA referred as VSS-MCMA-MDDMA. The step size is selected according to the distancedbetween the desired output and equalizer output in the constellation plane. During the equalization process, the regions ofy(k) can be located according theith point in the constellation diagram, as shown in Fig.4. Herei=1,2,…,M, andMis the order of the QAM signals.

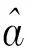
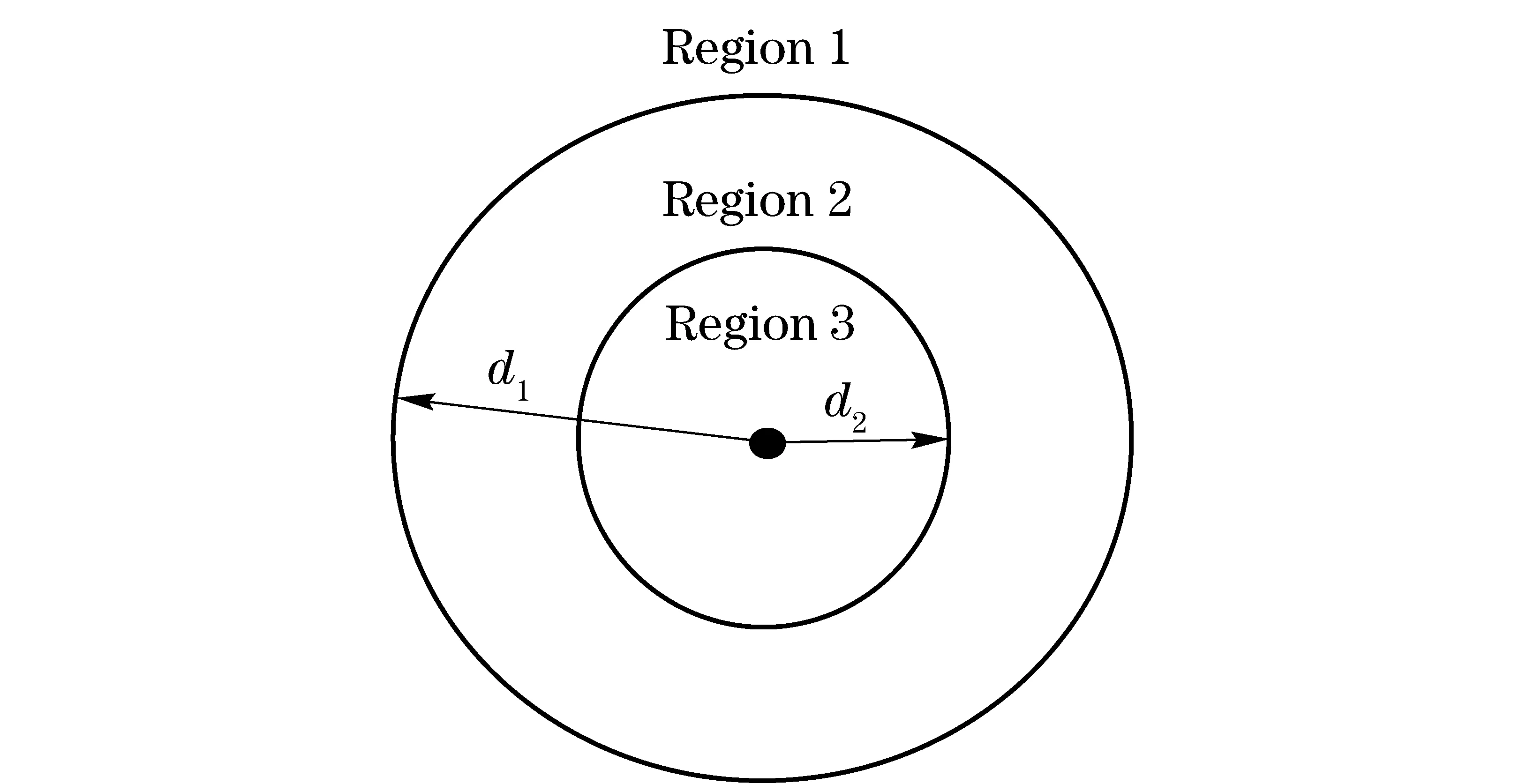
Fig.4 Regions defined around the ith point in the M-QAM constellation diagram

3 Simulation results

Simulationsarecarriedoutwiththefollowingscenario:transmitted16-QAMsymbolswithuniformdistributions,transversalequalizerwith21coefficientswheretheinitializationconsistsofsettingcentertapto1andothersto0,andtheSNRratioischosentobe35dB.Finally,atwo-tapfrequency-selectivechannelwithimpulseresponseisfixedash1=[10.129+0.046 3j] . The proposed combined MCMA-MDDMA with VSS is compared with CMA, MCMA, and MCMA-MDDMA with a fixed step size. The three step sizes for VSS-MCMA-MDDMA areμ1=0.000 05,μ2=0.000 03, andμ3=μ1/6. The regions 1, 2 and 3 are selected by choosingd1=0.6 andd2=0.2. The step size for CMA, MCMA and MCMA-MDDMA are allμ=0.000 02.

All the MSE curves are obtained by calculating the average over 200 Monte Carlo realizations with 20 000 symbols for each realization.

Results are shown in Fig.5. The obtained MSE of the VSS-MCMA-MDDMA at the steady state is approximately 2 dB, 5 dB and 10 dB better comparng with MCMA-MDDMA, MCMA, and CMA, respectively. Moreover the convergence speed of the VSS-MCMA-MDDMA is faster than other algorithms.

Fig.5 MSE curves using channel h1 for 16-QAM signals

We decrease the number of iterations from 20 000 to 10 000 iterations. The simulation results of Fig.6 show the MSE performance for the channelh1=10.129+0.046 3j.

Fig.6 MSE curves using channel h1 for 10 000 iterations

As shown from the MSE performance of Fig.6 when decreasing the number of iterations from 20 000 to 10 000, the proposed VSS-MCMA-MDDMA has the best performance in terms of convergence speed and the MSE at the steady sate. For example at the point of 3 000 iterations we observe that the MSE of the VSS-MCMA-MDDMA is -17 dB, and the MSE of MCMA, MCMA-MDDMA are -15 dB and -8 dB, respectively. In terms of convergence speed, the proposed VSS-MCMA-MDDMA is the fastest one that can converge after 3 800 iterations. The MCMA and MCMA-MDDMA converge after 6 000 and 4 000 iterations, respectively.

To examine the behavior of VSS-MCMA-MDDMA when the phase rotation problem is presented, the following simulations are done using frequency selective channelh2with two complex coefficientsc1=0.906 3+0.422 6j andc2=0.321 4+0.383 0j.

Fig.7 shows the signal constellation diagram using 16-QAM modulation of 2 000 to 20 000 symbols for CMA, MCMA, MCMA-MDDMA and VSS-MCMA-MDDMA. It can be seen that the VSS-MCMA-MDDMA can correct the phase error without a need for additional correction loop. In contrary, the CMA algorithm still presents a phase rotation at its output so it needs a phase looked loop (PLL) to correct the phase rotation. In another aspect, it has the clearest signal constellation when compared with MCMA and MCMA-MDDMA algorithms.

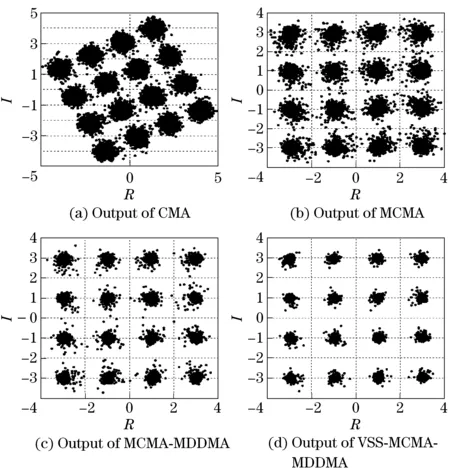
Fig.7 Constellations of 16QAM signals using channel h2 (2 000 to 20 000 symbols)

As shown in Fig.8, the CMA has the highest steady state MSE error due to the phase rotation caused by the channel. Meanwhile, the VSS-MCMA-MDDMA has a faster convergence and lower MSE than MCMA and MCMA-MDDMA.

Finally, the symbol error rate (SER) performances are investigated in Tab.1 and Tab.2 for the channelh1and channelh2, respectively. Due to the phase error, SER performance of CMA algorithm is quite poor. In contrast, the MCMA, MCMA-MDDMA and VSS-MCMA-MDDMA algorithms have better SER performance for the adoption of phase recovering process, i.e., VSS-MCMA-MDDMA has lowest SER.

Fig.8 MSE curves using channel h2 for 16-QAM signals

Tab.1 SER for 16-QAM signals using channelh1

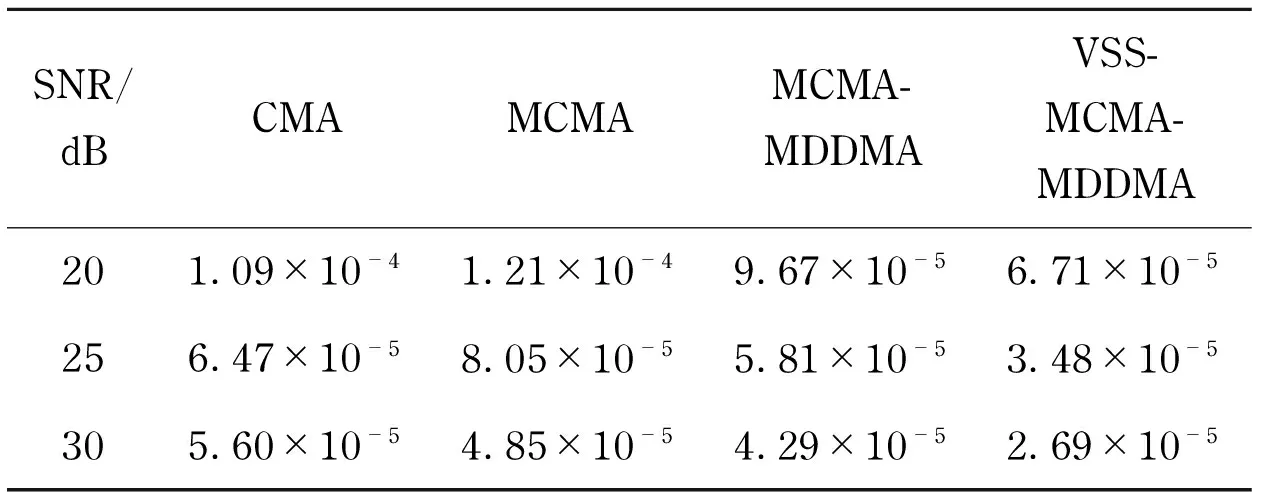
SNR/dBCMAMCMAMCMA-MDDMAVSS-MCMA-MDDMA201.09×10-41.21×10-49.67×10-56.71×10-5256.47×10-58.05×10-55.81×10-53.48×10-5305.60×10-54.85×10-54.29×10-52.69×10-5

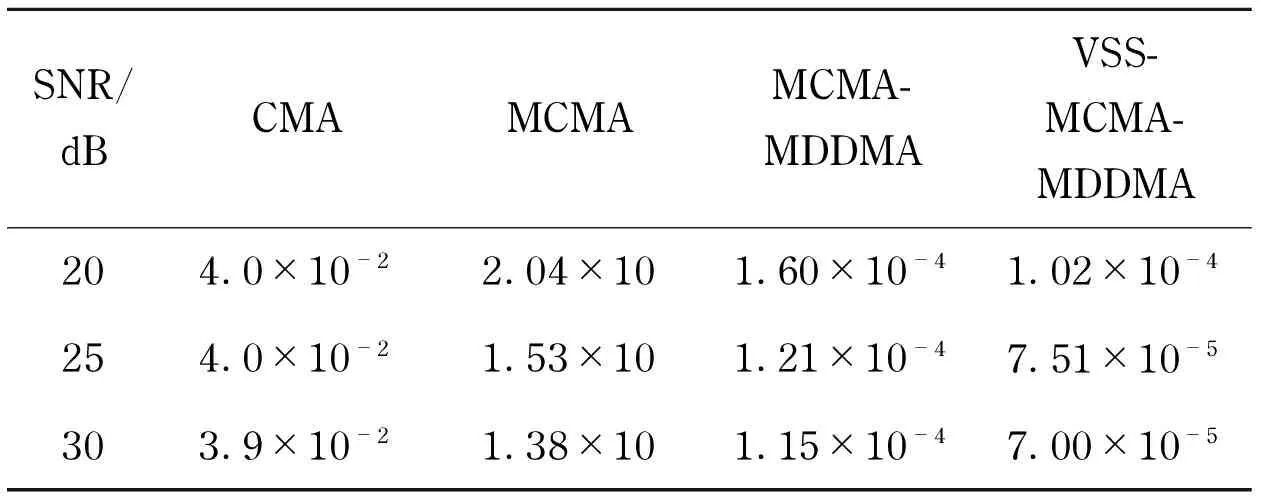
Tab.2 SER for 16-QAM signals using channel h2

4 Conclusion

A VSS blind equalization technique for QAM signals based on the distance between the output of equalizer and the desired output in the constellation plane is proposed. Using this technique, an application was tested on combined MCMA and MDDMA (MCMA-MDDMA). The results using 16-QAM signals show that the MCMA-MDDMA with VSS is better regarding both the convergence speed and steady state MSE. In addition, it can recover the phase.

[1] RAPPAPORT Theodore S. Wireless communications: principles and practice[M]. Upper Saddle River, New Jersey: Prentice Hall, 1996: 299-311.

[2] Benesty J, Duhamel P. A fast exact least mean square adaptive algorithm[J].Signal Processing, IEEE Transactions on, 1992, 40(12): 2904-2920.

[3] Cioffi J, Kailath T. Fast, recursive-least-squares transversal filters for adaptive filtering[J].EEE Transactions on, Acoustics, Speech and Signal Processing, 1984, 32(2): 304-337.

[4] Godard D. Self-recovering equalization and carrier tracking in two-dimensional data communication systems[J]. IEEE Transactions on Communications, 1980, 28(11): 1867-1875.

[5] Oh K N, Chin Y O. Modified constant modulus algorithm: blind equalization and carrier phase recovery algorithm[C]∥“Gateway to Globalization”, 1995 IEEE International Conference on Communications, Seattle, USA, 1995.

[6] He L, Amin M G, Reed Jr C, et al. A hybrid adaptive blind equalization algorithm for QAM signals in wireless communications[J]. IEEE Transactions on Signal Processing, 2004, 52(7): 2058-2069.

[7] Li X L, Zhang X D. A family of generalized constant modulus algorithms for blind equalization[J].IEEE Transactions on Communications, 2006, 54(11): 1913-1917.

[8] Zhao X, Guo Y, Rao W. Blind Equalization Algorithms Based on Orthogonal Wavelet and Coordinate Transformation[C]∥IHMSC’09. International Conference on Intelligent Human-Machine Systems and Cybernetics, Hangzhou, China, 2009.

[9] Labed A, Aissa-El-Bey A, Chonavel T, et al. New hybrid adaptive blind equalization algorithms for QAM signals[C]∥ICASSP 2009. IEEE International Conference on Acoustics, Speech and Signal Processing, Taibei, 2009.

[10] Fernandes C A R, Mota J C M. New Blind Algorithms Based on Modified “Constant Modulus” Criteria for QAM Constellations[C]∥Telecommunications and Networking-ICT 2004. Berlin: Springer, 2004: 498-503.

[11] Fernandes C A R, Mota J C M, Favier G. Decision directed algorithms for blind equalization based on constant modulus criteria[C]∥Colloque sur le Traitement du Signal et des Image, Louvain, Belgique, 2005.

[12] Fan C P, Liang W H, Lee W. Fast blind equalization with two-stage single/multilevel modulus and DD algorithm for high order QAM cable systems[C]∥IEEE International Symposium on Circuits and Systems, IEEE, 2008.

[13] Xue W, Yang X, Zhang Z. A variable step size algorithm for blind equalization of QAM signals[C]∥Progress In Electromagnetics Research Symposium, Cambridge, USA. 2010.

[14] Gao Y, Qiu X. A new variable step size CMA blind equalization algorithm[C]∥24th Chinese Control and Decision Conference (CCDC), Taiyuan, China, 2012.

(Edited by Cai Jianying)

10.15918/j.jbit1004-0579.201524.0315

TN 914.3 Document code: A Article ID: 1004- 0579(2015)03- 0381- 06

Received 2014- 02- 22

Supported by the National Natural Science Foundation of China (61002014; 61101129; 61227001; 61072050)

E-mail: lujihua@bit.edu.cn