Length estimation of extended targets based on bistatic high resolution range profile

QU Quan-you(屈泉酉), GUO Kun-yi(郭琨毅), SHENG Xin-qing(盛新庆)

(School of Information and Electronics, Beijing Institute of Technology, Beijing 100081, China)



Length estimation of extended targets based on bistatic high resolution range profile

QU Quan-you(屈泉酉), GUO Kun-yi(郭琨毅), SHENG Xin-qing(盛新庆)

(School of Information and Electronics, Beijing Institute of Technology, Beijing 100081, China)

The approach to estimate the length of extended targets by using the bistatic high resolution range profile (HRRP) is analyzed in this paper. The relationship between the bistatic HRRP and the monostatic HRRP of extended targets are investigated. It is demonstrated by simulations that the target length measured by the bistatic HRRP is more meaningful and accurate than that by the monostatic HRRP, though the monostatic HRRP has been well developed and widely used in target recognizing and classification. The estimation results of a cone shaped target are present and compared at the end of the paper. To assure the reliability of the simulation, the bistatic HRRP is obtained through the scattering field data calculated by a full-wave numerical method, FE-BI-MLFMA.

bistatic radar; high resolution range profile (HRRP); full-wave numerical method; length estimation

A bistatic radar system employs separate transmit and receive platforms by a large distance in space. It has many advantages compared with a monostatic radar system[1-4]. In a bistatic system, one or more receivers work cooperatively with a higher cost transmitting platform at a safe standoff distance, and the receivers provide multiple aspect looks of the target , which include more geometric information for target identification than a monostatic radar does[5-6]. In recent years, wideband bistatic imaging has become a research focus and has been widely used in target reorganization and classification. The high resolution range profile (HRRP) plays an important role in radar imaging and automatic target reorganization. The bistatic HRRP of point targets are used to extract the length of a target[7]. Length estimation of extended targets with the bistatic HRRP, however, has not been studied thoroughly.

In this paper, the bistatic HRRP of extended targets is investigated and compared with the monostatic HRRP. It is demonstrated that although the bistatic and monostatic HRRPs have similar forms, the range resolution is quite different. The bistatic HRRP shows the bistatic scattering information along the bisector of the bistatic angle.

The bistatic HRRP is simulated using the scattering field computed with the full-wave numerical method, the hybrid FE-BI-MLFMA[8-11]. The precise of this method has been well validated. The estimation result demonstrated that the target length measured by the bistatic HRRP is more meaningful and accurate than the monostatic HRRP.

1 Analysis of the bistatic HRRP

1.1 Geometry and signal model

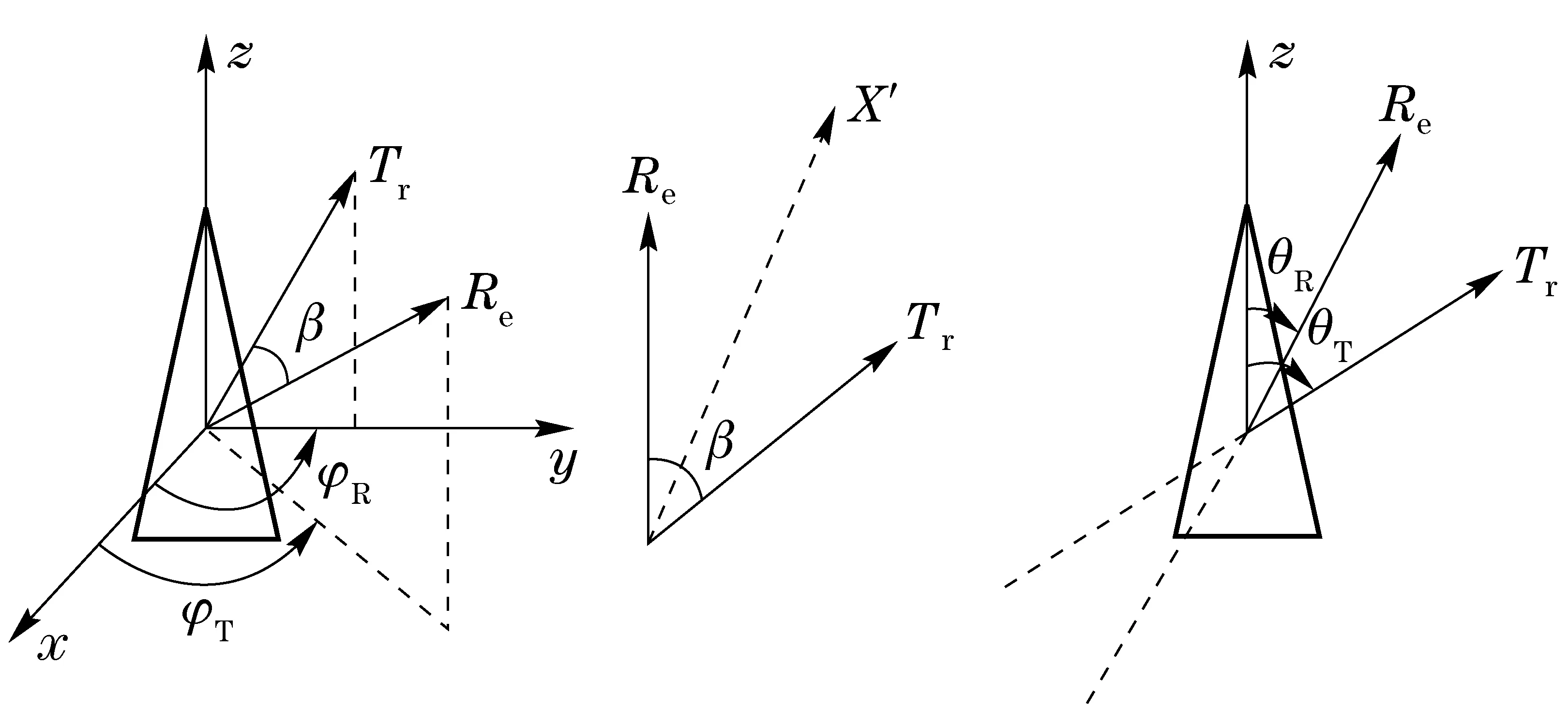
Fig.1 Geometry of the bistatic radar

Set the geometric center of the chosen target be the origin of the coordinate, and the ranges ofTrandReare denoted asRTandRR. The vectors of RTand RRcan be expressed by

(1)

(2)

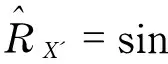
(3)

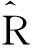
S(f)=

(4)

Thebistatichighresolutionrangeprofile(bi-HRRP)canbegottenbydoinginverseFouriertransformofEq.(4),andbeexpressedas

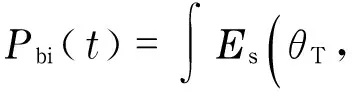
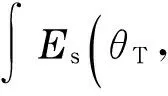
(5)

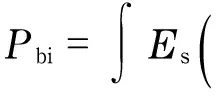
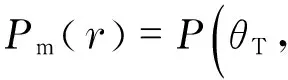
(6)

whererdescribes the range variable along the incident direction. Therefore,Pmcan represent the scattering centers distribution along the incident direction.

1.2 Bistatic and monostatic HRRPs

According to the scattering center theory[12], the high-frequency scattering response of an extended target can be approximated as the sum of responses from individual scattering centers. Therefore, we model the scattering response by the individual scattering centers as

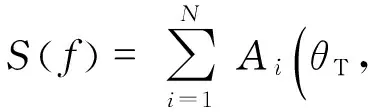
(7)

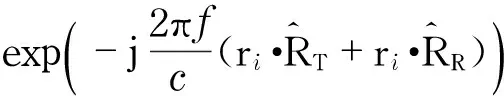
(8)

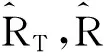
(9)

wherβis the bistatic angle of the bistatic radar system. Submitting Eq.(9) to Eq.(7), and Eq.(7) can be rewritten as

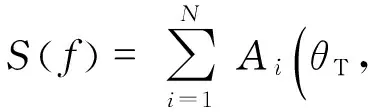
(10)

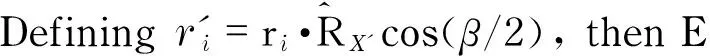
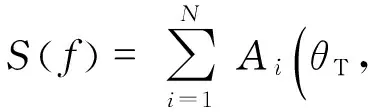
(11)

Thenthebi-HRRPcanbedescribedas

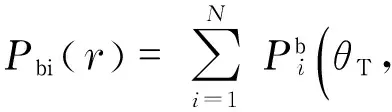
(12)

Similarly,wecangetthemon-HRRPofmultipleindividualscatteringcentersas

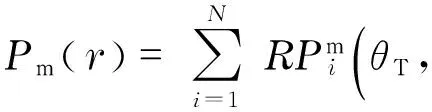
(13)

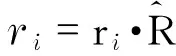
(14)

whereBis the band width of the bistatic radar system,c/(2B) is the range resolution of the monosatic radar. Eq.(14) shows that the bistatic range resolution Δrbiis closely related to the bistatic angle. This conclusion is apparently valid for measuring the ranges between isotropic scattering centers using the bistatic HRRP, as the scattering intensities are evenly distributed in the whole space. To measure the extended targets length using the HRRP is first to count the total number of the bistatic scattering centers demonstrated in a bi-HRRP image

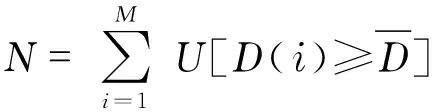
(15)

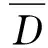
(16)

wherern,r1are the coordinate of thenth and the 1st SC.

2 Results

In this section, a perfectly conducting ballistic missile warhead is studied,and the dimensions are shown in Fig.2. The spectra of bistatic HRRPs are shown in Fig.3. Because the range resolution of bistatic radar varies with the bistatic angle, the spectra are modified through interpolation. And it is obvious that the curve blurs in large bistatic angles. The incident elevation angles are 0°, 30°, 50° and 100° in Fig.3a-Fig.3d, and the receive elevation angles change with step of 2°.Because the target is rotationally symmetric, both the incident and receive azimuth angles are chosen to be same and unchanged. To avoid the forward scattering, the bistatic angles change from 0° to 160°. The spectra of monostatic HRRPs are shown in Fig.4. The incident angleθTvaries from 0° to 180° with step of 1°.

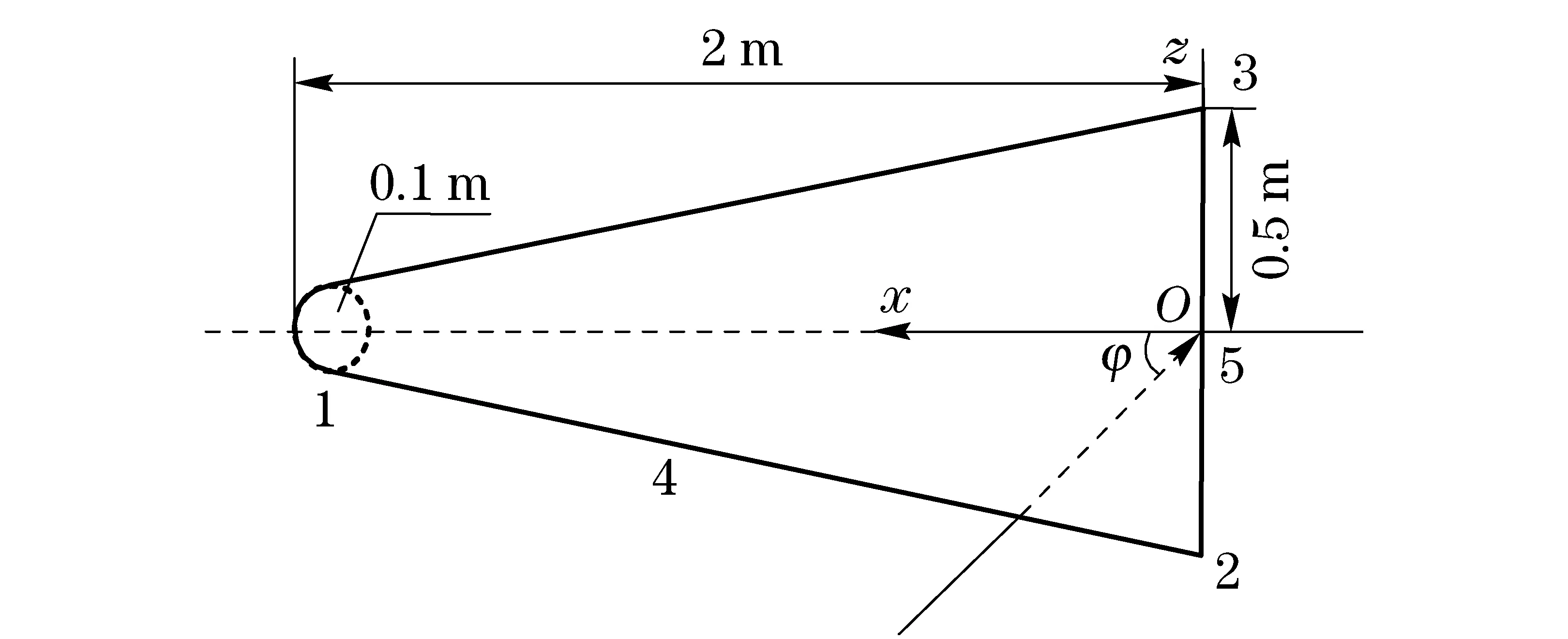
Fig.2 Geometry of a cone shaped missile warhead

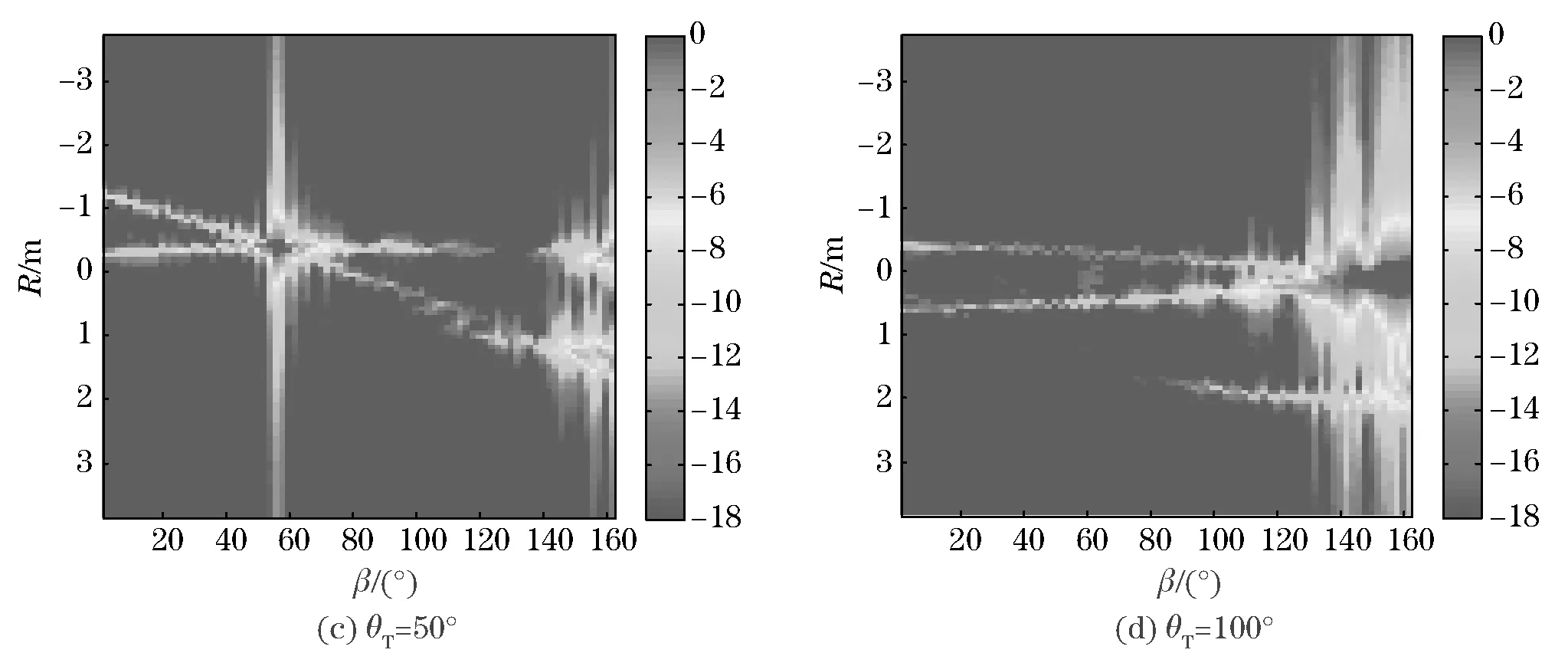
Fig.3 Spectra of bistatic HRRPs

Fig.5 Length measured by bistatic and monostatic HRRPs

Scattering center 1-3 marked in Fig.2 are shown in Fig.3 and Fig.4 as continuous curves. The vertical bright lines shown in Fig.3 comes from strong reflections of the cone side and bottom surface. The length measured through the HRRPs are actually the range between any two of SC1-3. The measurement results through Fig.3 are shown in Fig.5 with the legend of “bi”. The corresponding results through Fig.4 are shown in Fig.5 with the legend of “mon”. The theoretical ranges between the scattering centers are also shown as criterions. All measured curves are smoothed by omitting the wide value.

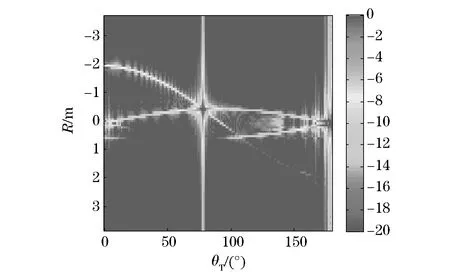
Fig.4 Spectra of monostatic HRRPs

It is demonstrated in Fig.4 that the bi-length coincides with the mon-length when the bistatic angleβis smaller than 80°, and varies asβincreases. The bi-lengths show different ranges of SC, and have new physical meanings as the receivers could provide different aspect looks of the target which include more geometric information for target identification than the monostatic radar does.

3 Conclusion

Bistatic HRRP through the data of a full-wave numerical method is derived in this paper. Relationships between the bistatic HRRP and the monostatic HRRP are studied. Although the monostatic HRRP has been well developed and widely used in target recognizing and classification, it is demonstrated that the target length measured by the bistatic HRRP (bi-length) is more meaningful and accurate. A preliminary study on the location and amplitude of bistatic scattering centers is presented by comparing the results with the monostatic cases.

[1] Jackson J A, Rigling B D, Moses R L. Canonical scattering feature models for 3D and bistatic SAR[J]. IEEE Transactions on Aerospace and Electronic Systems, 2010, 46(2): 525-541

[2] Jackson J A, Rigling B D, Moses R L. Parametric scattering models for bistatic synthetic aperture radar[C]∥Radar Conference RADAR’08, IEEE, NY, USA, 2008.

[3] Kell R E. On the derivation of bistatic RCS from monostatic measurements[J]. Proceedings of the IEEE, 1965, 53(8): 983-988.

[4] Qu Quanyou, Guo Kunyi, Mu Haijian, et al. Miss distance measurement based on stable scattering centers of extended targets[J]. Systems Engineering and Electronics, 2013, 35(4): 692-699. (in Chinese)

[5] Jackson J A. Analytic physical optics solution for bistatic, 3D scattering from a dihedral corner reflector[J]. IEEE Transactions on Antennas and Propagation, 2012, 60(3): 1486-1495.

[6] Qu Quanyou, Guo Kunyi, Sheng Xinqing. Precise target length estimation based on bistatic SC obtained through scattering characteristics analysis[J]. Journal of Beijing Institute of Technology, 2013, 22(Suppl 1): 95-99.

[7] Ai X, Li Y, Wang X, et al. Some results on characteristics of bistatic high-range resolution profiles for target classification[J]. Radar, Sonar & Navigation, IET, 2012, 6(5): 379-388.

[8] Guo K Y, Sheng X Q. Simulation research on scattering characteristics by complex targets[J]. Journal of Systems Engineering and Electronics, 2007, 18(4): 685-691.

[9] Guo K Y, Sheng X Q. A precise recognition approach of ballistic missile warhead and decoy[J]. Journal of Electromagnetic Waves and Applications, 2009, 23(14): 1867-1875.

[10] Gou Mingjiang, Wu Yueqian, Sheng Xingqing. Efficient solution of 3D electromagnetic scattering from large homogeneous targets[J]. Journal of Beijing Institute of Technology, 2013, 22(4): 524-529.

[11] Tian Zhongming, Guo Kunyi, Sheng Xinqing. Effects of surface roughness on monostatic RCS of corner reflector[J]. Transaction of Beijing Institute of Technology, 2011, 31(10): 1227-1230. (in Chinese)

[12] Keller J B. Geometrical theory of diffraction [J]. JOSA, 1962, 52(2): 116-130.

(Edited by Cai Jianying)

10.15918/j.jbit1004-0579.201524.0316

TN 95 Document code: A Article ID: 1004- 0579(2015)03- 0387- 05

Received 2014- 02- 28

Supported by the National Natural Science Fundation of China (61001192)

E-mail: guokunyi@bit.edu.com