固体含源导热问题的Hamilton原理及其解析方法

张文福

( 东北石油大学 防灾减灾及防护工程省高校重点实验室，黑龙江 大庆 163318 )



固体含源导热问题的Hamilton原理及其解析方法

张文福

( 东北石油大学 防灾减灾及防护工程省高校重点实验室，黑龙江 大庆 163318 )

变分原理的推导一般采用试凑法或Lagrange乘子法.基于固体瞬态热传导的微分方程，利用奥奇西克分部积分法建立固体含源导热问题的Hamilton原理.该原理可以用于构建新的有限元数值算法，也可以用于获得一些复杂边界问题的新解析解.分析Hamilton原理在热传导问题解析解方面的应用，利用康托洛维奇—里茨杂交法给出2个算例的近似解析解和精确解析解，从而证明建立的Hamilton原理及其解析解法的正确性和有效性.讨论基于热质理论的Hamilton 原理存在的问题.

Hamilton原理； 解析解； 变分法； 康托洛维奇—里茨杂交法

0 引言

经典分析力学由Newton I、Lagrange J L和Hamilton W R创立.其中Lagrange J L在《分析力学》中首次引入“广义坐标”的概念(现代振动力学中广泛使用的振型是一种“广义坐标”[1-2])，并建立Lagrange方程.然而，Lagrange方程是基于质点系力学建立的，仅适用于建立多自由度体系的运动方程，不适合描述连续介质的基本问题，并且不包含自然边界条件.Hamilton W R[3]将变分思想引入分析力学，拓展Lagrange方程，建立Hamilton原理.该原理不但形式简洁，还运用泛函求极值的方法，将真实运动从约束容许的一切可能运动中“挑选”出来，并且可以直接推出自然边界条件，从而克服Lagrange方程的缺点.经典分析力学的全部理论框架，包括Lagrange方程可以由Hamilton原理推演出来，并且Hamilton原理具有规范变换不变性，对现代理论物理的研究有重要价值.

Hamilton原理是否适用于非保守力系的问题一直存在争议.一些人提出用新的变分原理解决非保守力系问题，如Leipholz H[4]提出广义自共扼的概念，建立广义的Hamilton原理；刘殿魁等提出适合于分析非保守力系的“拟变分原理”[5].实际上，只要非保守力虚功的定义和变分运算正确，Hamilton原理同样适用于非保守力系问题，含热源导热问题也属于非保守力系问题，因而Hamilton原理同样适用于分析含热源导热问题.

与分析力学相比，热传导变分原理的提出较晚.最早的是由Onsager L提出的适合稳态导热过程的最小能量耗散原理，比较完善的变分原理是由Biot M A建立的.Biot M A[6]采用类比法，参照分析力学引入位移矢量场和广义坐标的概念，建立热传导的Lagrange方程；宋柏等[7-8]基于Einstein质能关系，给出热质运动需要满足的Hamilton原理和Lagrange方程，还利用建立的Lagrange方程给出含热源导热问题的近似解析解，为建立传热学提供新思路.笔者从变分原理角度讨论固体含热源导热问题.首先利用奥奇西克分部积分法[9]或梁立孚变积法[10]得到固体含热源导热问题的Hamilton原理；然后引入康托洛维奇—里茨杂交法，推导2个典型问题的近似解析解和精确解析解；最后讨论过增元提出的Hamilton原理.

1 微分方程与定解条件

设xi(i=1,2,3)为笛卡尔(Cartesian)坐标，采用哑标自动求和约定，根据传热学理论，在固体含源热传导问题中，任一点P(x1,x2,x3)的温度场T(x1,x2,x3,t)由微分方程和定解条件求得：

微分方程

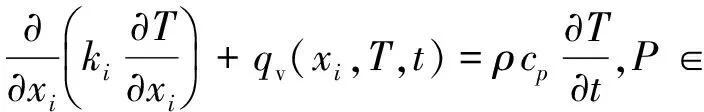
(1)

边界条件

T=Tw(xi,t),P∈S1;

(2)

(3)

初始条件

T(xi,0)=T0(xi),P∈V∪S.

(4)

式(1-4)中：ki为导热系数；ρ为密度；cp为比热；qv(xi,T,t)为体积热源强度；qsi(xi,T,t)为表面热流强度，流入区域为正；Tw(xi,t)为指定的边界温度；T0(xi)为初始的边界温度；V为求解区域；S为区域的全部边界，S=S1∪S2.

与经典传热学的“三类边界”划分方法[9]不同，文中仅需要指定两类边界，即温度边界及温度法向导数边界，其中后者为一种“广义边界”，包含第二类边界、第三类边界及其线性组合，既可以是位置和时间的函数，也可以是温度的函数.这种划分依据是变分原理，因为温度边界为指定“位移”边界，其变分为零；温度法向导数边界在变分原理中将以“非保守力虚功”的形式出现，且具有某种“外力”的特性，它与“位移”变分的乘积(虚功)通常不为零.

2 Hamilton原理

根据力学虚功原理，基于微分方程的变分逆运算，采用奥奇西克分部积分法[9]建立固体瞬态热传导的Hamilton原理，从而提供一种建立瞬态热传导(内含热源)问题泛函的简便方法.与奥奇西克分部积分法[9]类似，梁立孚变积法[10]实质上也是一种分部积分法.

首先将微分方程(1)乘以变分δT，并在时间和空间范围内进行积分，从而得到积分形式：

(5)

式中：dV为体积微元，dV=dx1dx2dx3.

然后采用分部积分法[9]，将式(5)的变分算子移到积分号外.对式(5)的第一项作分部积分：

(6)

根据边界条件(3)，将式(6)简化为

(7)

对式(5)的第三项作分部积分：

(8)

在时域边界t=t1和t=t2处取δT|=0[1-2]，有

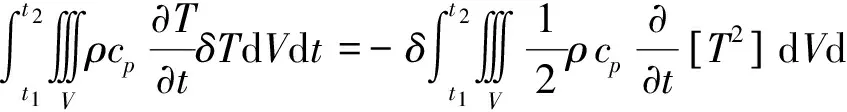
(9)

将式(7)和式(9)代入式(5)，得到

(10)

将式(10)与分析力学拓展的Hamilton原理[1-2]

(11)

进行类比，若令

动能

T*=0,

(12)

势能

(13)

系统耗散能

(14)

非保守力所做的虚功

(15)

则非定常热传导问题的温度场求解可以转化为分析力学的变分问题.

3 基于Hamilton原理的解析法及其应用

3.1 康托洛维奇—里茨杂交法

与瑞雷—里茨提出的待定系数法不同，康托洛维奇提出待定函数法[11]，为获得高精度的解析解提供理论基础.当泛函为

(16)

时，则将问题的解假设为

(17)

式中：φj(η)为预先选定的空间函数，根据边界条件选定；cj(τ)为待定的时间函数.与经典的分离变量法类似，隐含地假设时空函数可以由时间函数和空间函数的乘积叠加得到，对多数力学问题是适用的.

将假设的空间函数φj(η)代入泛函，利用泛函的驻值条件，可以导出关于cj(τ)的常系数微分方程，从而结合初值条件解出cj(τ)，即为康托洛维奇—里茨杂交法的基本思路[12].因为空间函数φj(η)和根据变分条件求得的时域函数cj(τ)为解析形式，故利用康托洛维奇—里茨杂交法可以获得问题的解析解.如果空间函数φj(η)能够精确满足边界条件，则将获得精确解析解；否则，为近似解析解.

若将连续体划分为若干单元，将康托洛维奇—里茨杂交法应用于每个单元分析，则可建立一种新型的有限元计算格式.

结合文献[7-8]给出的2个算例，利用文中提出的Hamilton原理分别推演问题的近似解析解和精确解析解.

3.2 算例1

考虑区域为00 ℃时,平板有定常的内热源qv(x,T,t)=q0，求平板温度分布的近似解析解.

根据康托洛维奇—里茨杂交法，取算例1的温度场为

(18)

(19)

式中：f1(t)为待定的时间函数，采用变分方法得到.

式(18)的空间函数满足平板两侧的热边界条件，为可用试函数.计算Hamilton原理中各项能量及其变分的公式为

(20)

(21)

(22)

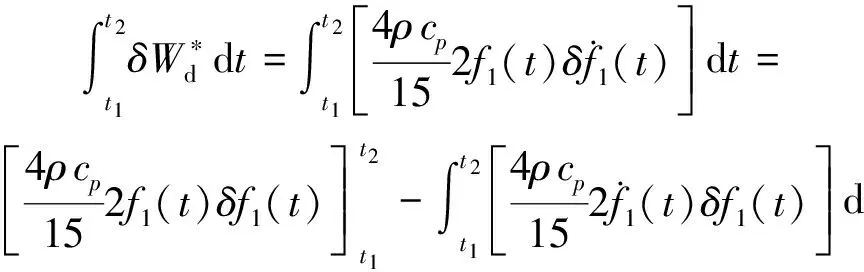
(23)

利用Hamiliton原理的端点变分条件[1-2]，式(23)右端的第一项结果应该为零，则变为

(24)

(25)

将式(21)、式(24)和式(25)代入式(11)得到

(26)

因为δf1(t)具有任意性，式(26)积分成立的条件应是方括号内的结果为零，即

(27)

或者

(28)

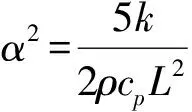
式(28)是关于时间函数f1(t)的一阶常系数微分方程，其解为

(29)

式中：A1为待定系数，根据初始条件确定，如将式(29)代入式(18)得到

(30)

根据初始条件

(31)

得

(32)

从而得到温度场的近似解析解为

(33)

若温度场取为无穷级数形式，即

(18b)

则根据文中提出的Hamiliton原理和康托洛维奇—里茨杂交法，还可以方便地求得算例1的精确解析解为

(34)

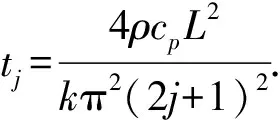
3.3 算例2

考虑区域为00 ℃时，平板有随时间变化的内热源qv(x,T,t)=q0sin2t，求平板的温度分布的精确解析解.

文献[8]给出算例2的近似解析解，文中基于康托洛维奇—里茨杂交法和建立的Hamilton原理给出精确解析解.首先算例2的温度场写成无穷级数表达形式

(35)

(36)

式(35)的空间函数满足平板两侧的边界条件，为可用试函数.计算Hamilton原理中各项能量及其变分的公式为

(37)

(38)

利用Hamiliton原理的端点变分条件[1-2]，式(38)右端的第一项结果应该为零，则变为

(39)

(40)

将式(37)、式(39)和式(40)代入式(11)得到

(41)

因为δfj(t)具有任意性，则式(41)积分成立的条件是方括号内的结果为零，从而得到

(42)

这是关于待定时间函数fj(t)的一阶常系数微分方程，其精确解析解为

(43)

式中：Aj为根据初始条件确定的待定系数.

将式(43)代入式(35)，由初始条件

(44)

(45)

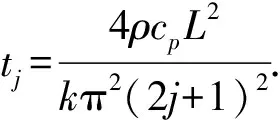
文献[8]用Lagrange方程仅能得到算例2的一阶近似解析解，根据文中提出的Hamilton原理和康托洛维奇—里茨杂交法能得到问题的精确解析解.

4 讨论

(1)利用所建立的Hamilton原理，可将真实温度场从约束容许的一切可能温度场中“挑选”出来，得到固体含热源导热问题的精确解析解.

(2)人们试图给出传热和传质问题的完全积分型的变分原理，因为完全积分型的泛函为二次型，积分简单，且容易按常规方法进行变分运算.BruceAF[13]评述各种完全积分型的变分原理，认为不存在变物性或瞬态热问题的完全积分型的变分原理.以文中建立的Hamilton原理为例，若将它改写表达为

(46)

(47)

[1] 克拉夫 R W,彭津 J.结构动力学[M].2版.北京:科学出版社,2007. Ray Clough, Joseph Penzien. Structural dynamics [M]. Beijing: Science Press, 2007.

[2] 王光远.应用分析动力学[M].北京:人民教育出版社,1981. Wang Guangyuan. Application analysis of dynamics [M]. Beijing: People's Education Press, 1981.

[3] Hamilton W R. On a general method in dynamics [J]. Philosophical Transaction of the Royal Society Part I, 1834:247-308; Part II, 1835:95-144.

[4] Leipholz H. Direct variational methods and eigenvalue problems in engineering [M]. Leyden: Noordhoff International Publishing, 1977.

[5] 刘殿魁,张其浩.弹性理论中非保守问题的一般变分原理[J].力学学报,1981(6):562-570. Liu Diankui, Zhang Qihao. Some general variational principles for nonconservative problems in theory of elasticity [J]. Chinese Journal of Theoretical Applied Mechanics, 1981(6):562-570.

[6] Biot M A. Variational principles in heat transfer [M]. Oxford: Clarendon Press, 1970.

[7] 宋柏,吴晶,过增元.基于拉格朗日方程的含源导热问题分析[J].工程热物理学报,2011,32(11):141-144. Song Bai, Wu Jing, Guo Zengyuan. Analysis of heat conduction problem involving heat source using lagrangian equation [J]. Journal of Engineering Thermophysics, 2011,3(1):141-144.

[8] 宋柏,吴晶,过增元.基于热质理论的Hamilton原理[J].物理学报,2010,59(10):7129-7133 Song Bai, Wu Jing, Guo Zengyuan. Hamilton's principle based on thermomass theory [J]. Acta Physica Sinica, 2010,59(10):7129-7133.

[9] Ozisik M N.热传导[M].北京:高等教育出版社,1983. Ozisik M N. Heat conduction [M]. Beijing: Higher Education Press, 1983.

[10] 梁立孚,石志飞.关于变分学中逆问题的研究[J].应用数学和力学,1994,15(9):775-788. Liang Lifu, Shi Zhifei. On the inverse problem in calculus of variations [J]. Applied Mathematics and Mechanics, 1994,15(9):775-788.

[11] 钱伟长.广义变分原理[M].北京:知识出版社,1985. Qian Weichang. Generalized variational principle [M]. Beijing: Knowledge Press, 1985.

[12] 刘高联,宋雪玉,李范春.康托洛维奇—里茨杂交法及其应用[J].力学季刊,2007,28(3):383-388. Liu Gaolian, Song Xueyu, Li Fanchun. Kantorovich-Ritz hybrid method and its applications [J]. Chinese Quarterly of Mechanics, 2007,28(3):383-388.

[13] Bruce A F. The method of weighted residuals and variational principles: With applications in fluid mechanics, heat and mass transfer [M]. New York: Academic Press, 1972.

2015-01-10；编辑：朱秀杰

国家自然科学基金项目(51178087，51176023)；黑龙江省教育厅重点项目(12511Z004)

张文福(1965-)，男，博士，教授，主要从事结构工程、工程抗风、抗震及抗火方面的研究.

TK121

A

2095-4107(2015)03-0118-08

DOI 10.3969/j.issn.2095-4107.2015.03.015