多普勒跟踪测量用于时空引力检验的尝试：(Ⅰ)理论建模

邓雪梅，谢懿

(1.中国科学院 紫金山天文台，南京 210008；2.南京大学 天文与空间科学学院，南京 210093； 3.上海市空间导航与定位技术重点实验室，上海 200030)

多普勒跟踪测量用于时空引力检验的尝试：(Ⅰ)理论建模

邓雪梅1，谢懿2，3

(1.中国科学院 紫金山天文台，南京 210008；2.南京大学 天文与空间科学学院，南京 210093； 3.上海市空间导航与定位技术重点实验室，上海 200030)

作为多普勒跟踪测量用于时空引力检验的尝试，在多普勒建模过程中加入了对于局部洛仑兹不变性(LLI)以及局部位置不变性(LPI)的检验参数。LLI/LPI是包括广义相对论在内的任何度规引力理论的基石。通过迭代求解多普勒建模过程中所需的光行时解，证明了只有在单程以及三程多普勒测量中可以检验LLI和LPI。鉴于该种测量手段无需额外载荷以及我国测控精度，可以尝试通过单/三程多普勒测量来检验LLI和LPI的科学目标。

多普勒跟踪测量；引力；深空探测

0 引 言

作为目前测控与导航的极其重要手段之一，单程、双程以及三程多普勒跟踪测量已经成功地实施在许多探测任务中[1-2]。与此同时，多普勒测量数据还可用于各种各样的科学研究，比如基本物理学。通过测量卡西尼土星探测器与地球通讯过程中的频率变化，Bertotti等(2003)[3]得到了太阳系中对于广义相对论验证的一个强有力限制。此外，多普勒跟踪测量很可能是测量低频引力波(10-5～1 Hz)的唯一方式[4]。本文将主要探讨多普勒测量用于广义相对论最基本检验——爱因斯坦等效原理(EEP)——的可能性。

EEP不但是建立广义相对论的基础，而且是涵义更为广泛的整个弯曲时空理论的基石。它包含三大要素[5]，分别是：弱等效原理(WEP)、局部洛仑兹不变性(LLI)和局部位置不变性(LPI)。它们的具体内涵如下：WEP，任何自引力可忽略物体的惯性质量等于它的引力质量；LLI，任何局部非引力实验的结果不依赖于该实验所在参考系的自由下落速度；LPI，任何局部非引力实验的结果不依赖于该实验所进行的时间和地点。其中LLI和LPI可以通过测量处于天体引力场中原子钟频率的变化来进行检验[6]。

1976年，美国宇航局发射了引力探测器A(GP-A)。该探测器携带了一台氢原子钟，其距离地面的高度为10 273 km。该实验主要是比较这台空间钟和地面钟之间的频率来检验EEP，其精度约为7×10-5[7]。1980年，“旅行者1号”/“旅行者2号”飞掠土星的过程中首次在地球以外引力场中检验了EEP，其精度为1%[8]。1990年，伽利略木星探测器飞掠金星和地球的过程中在0.5%精度下检验了EEP[9]。

上述实验依赖于探测器同地面通信的单程多普勒测量。探测器上的转发频率参照星上频率标准，地面站接收的频率则参照地面频率标准。然而，对于探测器跟踪精度而言单程多普勒测量存在许多问题。星上频率标准没有地面频率标准稳定，且受到自身噪声影响。解决方案之一是使用双程多普勒测量。在双程模式中，地面站参照一个高质量频率标准来发射一个无线电信号。随后，探测器接收到这个信号并通过相位相干转发到地面站。转发过程中加入目前观测中可忽略不计的噪声，这个转发过程并不需要在探测器上放上一个好的原子钟[4]。双程多普勒测量形成了信号的一个封闭循环。相反，三程模型的发射站和接收站不是同一个。因此，三程多普勒测量形成了信号的一个开放循环。

本文在单程多普勒测量模型基础上，主要给出考虑LLI/LPI在内的双/三程多普勒建模过程；通过光行时求解星上发射时刻；针对我国未来有望实施的金/火星探测任务，就在广义相对论实验检验中可开展的自主研究与实践给出建议。

1 模 型

本节将从单程多普勒模型出发[9]，建立在太阳系质心参考系(BCRS)下考虑了LLI/LPI效应的双/三程多普勒跟踪测量模型。

1.1 单程多普勒建模

EEP预言了频率变化[10]。观测到的红移量z定义如下

(1)

其中：νE(tE)是在tE时的发射频率；νR(tR)是在tR时的接收频率。

在下面推导中，除非有特别说明，否则忽略掉计算量中的时刻，如νE≡νE(tE)，νR≡νR(tR)。在ε2阶数上(其中ε≡1/c，c为光速)，方程(1)为[11]

(2)

(3)

(4)

式(2)中，速度项全部源自狭义相对论，而引力项则源自广义相对论。

为了检验LLI/LPI，单程多普勒测量模型为

(5)

(6)

(7)

下面通过式(6)来建立包含LLI/LPI在内的双/三程多普勒测量模型。

1.2 双程多普勒建模

在双程多普勒跟踪测量中，地面站S在tE时发射的信号频率为νE；探测器P在t′时接收到这个信号，其频率为ν′；随后，探测器P立即将接收到的频率乘以q转发(q为已知的两个整数之比)，此时发射的频率为qν′；最后，地面站S在tR时接收到这个信号频率为νR。整个过程可以看成是两个单程测量，即

(8)

将两个依赖不同发射时刻及接收时刻的单程多普勒测量模型代入式(8)，便可得到双程多普勒测量的详细表达式。

1.3 三程多普勒建模

在三程多普勒测量中，存在两个地面站。地面站S1发射信号，地面站S2接收由探测器P转发的这个信号。在这个开放循环中，频率移动为

(9)

将两个依赖不同发射时刻及接收时刻的单程多普勒测量模型代入式(9)，便可得到三程多普勒测量的详细表达式。

虽然上述理论模型已经建立，但这些模型并不能直接应用，其原因是探测器上的发射时刻t′不可知，它需要通过光行时求解并最终使建立的模型全部依赖于接收时刻tR[2]。

2 光行时解

光行时解是建立在信号往返时间间隔的基础上[2]。通常，发射时刻tE和接收时刻tR有如下关系

(10)

其中：第二项为弯曲时空引起的Shapiro时间延迟[12]。当信号由木星发出并近距离经过太阳，最终到达地球，由太阳造成的Shapiro时延会达到10-4s；当信号由土星发出并近距离经过木星，最终到达地球，由木星造成的Shapiro时延会达到10-7秒；对于单程情况，当信号由土星发出并近距离经过地球而到达地面站，由地球造成的Shapiro时延会达到10-10s。太阳系中Shapiro时延的量级要比多普勒测量中发射和接收的平移运动以及转动时标小很多，因此在光行时解中可以忽略掉Shapiro时延，即

(11)

可以通过迭代方法数值求解发射时刻，在本文中我们采用分析方法求解。在多普勒测量中，发射者和接收者的轨道运动时标通常远大于光线传播的时标(即，光行时)Δt，因此可以得到如下关系

(12)

(13)

(14)

(15)

实际应用中，多普勒模型可以仅依赖于接收时刻。

2.1 考虑光行时解的单程多普勒建模

根据式(14)和(15)，随接收时刻tR变化的单程多普勒模型可写成

(16)

(17)

于是，可得到考虑LLI/LPI破坏下单程多普勒测量随接收时刻tR的变化

(18)

(19)

2.2 考虑光行时解的双程多普勒建模

在双程多普勒测量中，考虑光行时解的模型建立如下

(20)

(21)

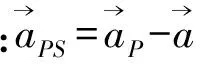
2.3 考虑光行时解的三程多普勒建模

同单/双程建模类似，考虑光行时解的三程多普勒测量模型如下

(22)

(23)

(24)

3 结 论

多普勒跟踪测量不但是保证许多探测器成功实施的任务支撑，还可用于探测任务的科学研究，如检验时空引力的基本性质。本研究工作从单程多普勒测量入手，推导出包含LLI/LPI在内的双/三程多普勒模型。进一步通过光行时方程求解星上发射时刻，最终获得了用于检验LLI/LPI的仅依赖于接收时刻的双/三程多普勒测量模型。

鉴于目前国际上已存在许多以时空引力研究为着眼点的探测任务，针对我国未来有望实施的金星/火星探测任务，最后我们就在广义相对论实验检验中可开展的自主研究与实践给出建议。简单来说，对时空引力的实验检验大致可分为3步。第1步，利用星上已有载荷。例如，针对有望于未来开展的我国自主火星/金星探测任务，使用多波段无线电通讯系统，开展以多普勒跟踪以及测距观测为基础的引力实验。第2步，研制专门载荷。搭载为检验某一效应而专门研制的载荷，例如高精度原子钟或者激光测距系统等。第3步，发射以检验广义相对论为首要科学目标的专门探测器。对于这3步而言，研发成本、硬件制造难度、科学产出以及任务潜在风险均逐级递增。对于我国尚处于起步阶段的空间探测计划，建议从第1步做起，在积累了足够的经验之后再实施后续难度更高的步骤，而且该步的优点在于无需额外载荷，这也为我国测控开展相关研究带来了可能性。以X波段为例，本文初步评估了在地月、地火多普勒测量中对于LLI和LPI探测的可能性。结论为：在单程多普勒中可以同时测量LLI和LPI；在三程多普勒中以目前精度而言，仅可以测量LLI。在我们后续的研究工作中，将会给出利用我国测控数据来检验时空引力的探测可能性。

[1]CatherineL.深空导航无线电跟踪测量技术[M].李海涛，译.北京：清华大学出版社，2005. [CatherineL.Deepspacenavigationradiotrackingmeasurementtechnology[M].LiHT，transl.Beijing:TsinghuaUniversityPress，2005.]

[2]MoyerTD，YuenJH.Formulationforobservedandcomputedvaluesofdeepspacenetworkdatatypesfornavigation:jetpropulsionlaboratory，nationalaeronauticsandspaceadministration[M].JPLPublication00-7， 2000.

[3]BertottiB，IessL，TortoraP.AtestofgeneralrelativityusingradiolinkswiththeCassinispacecraft[J].Nature， 2003，425(6956):374-376.

[4]ArmstrongJW.Low-frequencygravitationalwavesearchesusingspacecraftdopplertracking[J].LivingReviewsinRelativity， 2006，9(1):1-60.

[5]WillCM.Theoryandexperimentingravitationalphysics[M].Cambridge，UK:CambridgeUniversityPress，1993．

[6]KrisherTP.Newtestsofthegravitationalredshifteffect[J].ModernPhysicsLettersA， 1990,5(23):1809-1813．

[7]VessotRFC，LevineMW，MattisonEM，etal.Testofrelativisticgravitationwithaspace-bornehydrogenmaser[J].PhysicalReviewLetters， 1980，45(26):2081-2084．

[8]KrisherTP，AndersonJD，CampbellJK.TestofthegravitationalredshifteffectatSaturn[J].PhysicalReviewLetters， 1990，64(12):1322-1325．

[9]KrisherTP，MorabitoDD，AndersonJD.TheGalileosolarredshiftexperiment[J].PhysicalReviewLetters， 1993，70(15):2213-2216.．

[10]MisnerCW，ThorneKS，WheelerJA.Gravitation[M].SanFrancisco:W.H.FreemanandCo.， 1973．

[11]BrumbergVA.Essentialrelativisticcelestialmechanics[M].Bristol:AdamHilger， 1991．

[12]ShapiroII.Fourthtestofgeneralrelativity[J].PhysicalReviewLetters， 1964，13(26):789-791．

[责任编辑：高莎]

The Trial of Probing Gravitation with Spacecraft Doppler Tracking : (I) Modeling

DENG Xuemei1， XIE Yi2，3

(1.Purple Mountain Observatory， CAS， Nanjing 210008， China; 2.Department of Astronomy， Nanjing University， Nanjing 210093， China； 3.Shanghai Key Laboratory of Space Navigation and Position Techniques， Shanghai 200030， China)

Currently two-way and three-way spacecraft Doppler tracking techniques are widely used and play important roles in control and navigation of deep space missions. Starting from a one-way Doppler model， we extend the theory to two-way and three-way Doppler models by making them include possible violations of the local Lorentz invariance (LLI) and the local position invariance (LPI) in order to test the Einstein equivalence principle， which is the cornerstone of general relativity and all other metric theories of gravity. After taking the finite speed of light into account， which is the so-called light time solution (LTS)， we make these models depend on the time of reception of the signal only for practical convenience. We find that possible violations of LLI and LPI cannot affect two-way Doppler tracking under a linear approximation of LTS， although this approximation is sufficiently good for most cases in the solar system. We also know that， given the accuracy of measurement and control in China and no additional payload in this method， possible violations of LLI and LPI could be the scientific goals of Chinese measurement and control．

Doppler tracking; gravitation; deep space exploration

2014-10-14

2015-02-10

国家自然科学基金(11473027，11103085)；江苏省自然科学基金(BK20131461);上海市空间导航与定位技术重点实验室基金(14DZ2276100)

P129

A

2095-7777(2015)02-0186-06

10.15982/j.issn.2095-7777.2015.02.014

邓雪梅(1978—)，女，博士，副教授，主要研究方向：相对论天体测量。通信地址：江苏省南京市北京西路2号(210008)电话：(025)83332137E-mail：xmd@pmo.ac.cn谢懿(1981—)，男，博士，副教授，主要研究方向：基本天文学。通信地址：江苏省南京市汉口路22号南京大学天文与空间科学学院(210093)电话：(025)89681230E-mail:yixie@nju.edu.cn