液压阀控系统的前馈-自调整因子模糊控制

于浩洋

(黑龙江工程学院 电气与信息工程学院,黑龙江 哈尔滨 150050)

液压阀控系统的前馈-自调整因子模糊控制

于浩洋

(黑龙江工程学院 电气与信息工程学院,黑龙江 哈尔滨 150050)

针对液压阀控系统负载的不确定性和扰动性，建立液压阀控系统的数学模型，设计出前馈和自调整因子模糊控制相结合的控制方法，同时分析模糊控制器的控制机理，给出自调整因子模糊控制器的基本结构，在MATLAB/SIMULINK环境下进行仿真验证。仿真结果表明这种控制方法能有效地提高控制系统的控制性能，自调整因子模糊控制和前馈控制环节的结合在液压阀控伺服系统的控制中具有很好的控制效果。

前馈；自调整因子；液压阀控系统；负载扰动；仿真

液压阀控系统是工程上常用的伺服控制系统,它具有响应速度快、功率/重量比大、负载刚性高和性能价格比高等特点,能实现高精度、高速度和大功率的控制，因此,在航空航天、冶金、船舶、机床、动力设备和煤矿机械等工业领域得到了广泛应用。近年来,国内外学者对于液压阀控进行了许多控制策略方面的研究,如非线性PID控制[1]、QFT鲁棒控制[2]、变结构控制[3]和H∞控制[4]等,均取得了一定的成果。然而由于系统中存在的非线性因素,如系统载荷随机多变性、扰动随机性及液压系统本身具有的油液非线性特性等,使得常规的、基于线性模型的控制策略无法达到期望的系统性能要求。因此，分析不同形式的伺服阀及其阀控制缸机构的非线性特性,建立相应的非线性数学模型，以便能更加细致地描绘实际的阀控系统,为研究适合高性能的系统控制策略提供必要的保障。

本文提出利用前馈与自调整因子模糊控制相结合的办法，对阀控系统进行跟踪控制。

1 液压阀控系统建模

假定：阀是零开口四边滑阀，4个节流窗口是匹配和对称的，供油压力PS恒定，回油压力P0为0，阀的线性化流量方程为

(1)

式中:Kq为流量增益，Kc为流量压力系数，xv为伺服阀主阀位移，pL为负载压力。

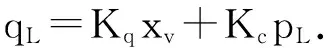
(2)

液压缸的连续性方程

(3)

式中：Ap为液压缸活塞有效面积，xp为滑阀位移，Ctp为液压缸总泄漏系数，Vt为液压缸控制腔初始容积，βe为油液等效容积模量。

液压缸的输出力与负载力的平衡方程

(4)

式中:M为活塞及负载总质量,Bp为活塞及负载的黏性阻尼系数,K为负载弹簧刚度,FL为作用在活塞上的任意外负载力。

将式(2)、式(3)、式(4)进行拉式变换，消去中间变量pL，并整理得

(5)

式中：Kce为总压力—流量系数，Kce=Ctp+Kc。

(6)

由于液压执行机构的固有频率高于50Hz，所以本文按液压缸负载固有频率与伺服阀频宽相近来确定，电液伺服阀的传递函数按二阶振荡环节取用[5]

(7)

式中：Ksv为伺服阀的流量增益，ωsv为伺服阀固有频率，ξsv为伺服阀阻尼系数。

整个电液系统的数学模型如图1所示。

图1 电液伺服系统模型

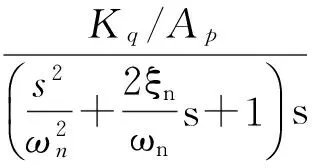
由此可得系统的状态空间模型为

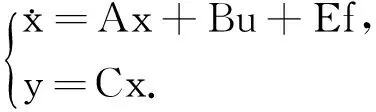
(8)

其中：

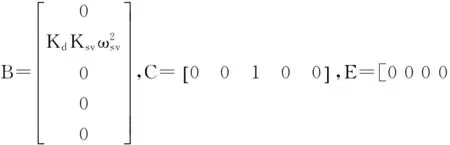
2 前馈-反馈跟踪控制的设计

伺服系统不仅本身是非线性系统, 而且由于其系统载荷的随机多变性、扰动随机性及液压系统本身具有的油液非线性特性等,使得常规的、基于线性模型的控制策略无法达到人们所期望的性能要求。为了发挥其响应速度快、调速范围广、功率大、耐用性高等优点，本文采用前馈控制结合反馈控制的跟踪控制策略，即由前馈控制减小系统中存在由加入固定负载引起常值扰动，由前馈和自调整因子模糊控制来尽可能地控制和减小由负载变化引起的扰动惯性，系统控制如图2所示。

图2 系统控制方案

图中Gq(s)=Gsv(s)Kq/AP。

2.1 前馈控制

前馈控制是指在控制系统中,根据设定值或者外界干扰的变化，产生合适的控制作用去改变操纵变量,使受控变量维持在设定值上的一种控制方法[6]。由于系统载荷的随机多变性以及扰动随机性的存在，使扰动的测量十分困难，但是扰动最直接的表现就是体现在滑阀位移大小的改变上，并具有一定的惯性。因此，在前馈通路中设有相应的控制环节，就可以尽可能地减少、甚至消除由于负载常值扰动对系统的影响，同时也可以和自调整因子模糊控制器一起控制和减小由于负载变化引起的扰动的惯性对系统产生的影响。本文在前馈通道上采用PID控制器对扰动直接进行控制，并由此使系统由于扰动产生的影响直接在前向通道予以补偿。这样，主通道上的控制输出就由主控制器和前馈补偿两部分组成，从而完成对负载扰动的一种跟踪补偿控制。前馈控制如图3中虚线内部所示。

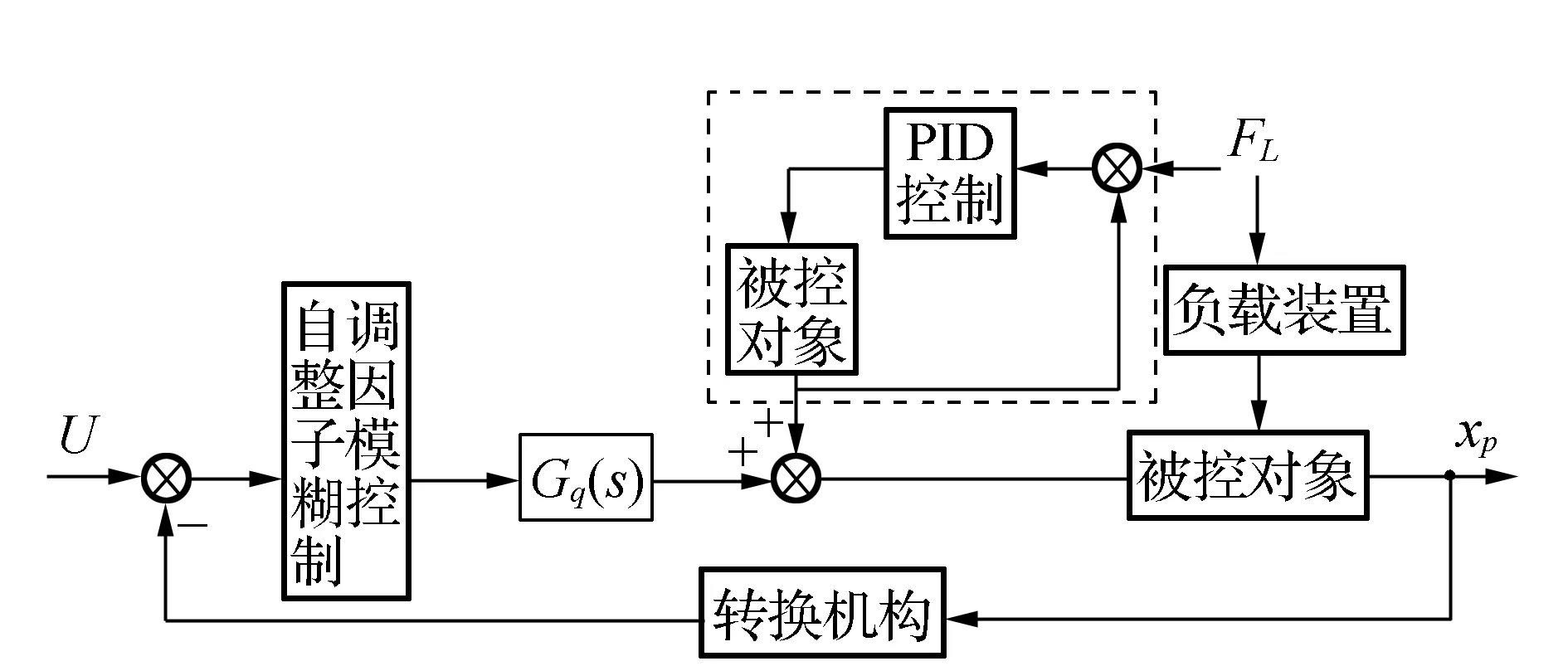
图3 前馈控制系统

2.2 自调整因子模糊控制

模糊控制由于具有不依赖被控对象的精确数学模型、设计简单、鲁棒性强以及良好的非线性控制特性等特点，在工业过程控制等领域得到了广泛的应用，并已成为智能控制的一个主要分支。但是采用常规模糊控制的最大问题就是存在稳态误差。为了减小甚至消除稳态误差，本文采用带自调整因子的模糊控制器。该控制器通过修正因子来改变控制规则，再用优化的控制规则进行控制，也就是通过对模糊规则的调整从根本上提高模糊控制器的性能，其结构如图4所示。

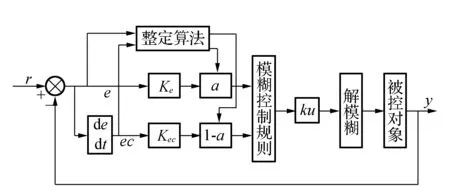
图4 自调整因子模糊控制系统

图4中各个参数的意义为：r，y分别为系统的设定值和系统的输出值(精确量)；e，ec，u分别为系统误差、误差变化率和模糊控制器的控制输出(精确量)；E，Ec，U分别为反映系统误差、误差变化率和模糊控制器输出(模糊量)。

通常情况下，fuzzy模型结构可用下列解析式表示

自调整因子α由模糊推理产生，相当于在原常规的模糊控制器基础上增加一个用于调整加权因子α的模糊控制器。这样就可以满足当误差较大时，控制系统的主要任务是消除误差，这时对误差在控制规则中的加权应该大些；相反当误差较小时，此时系统已接近稳态，控制系统的主要任务是使系统尽快稳定。

3 控制系统仿真及分析

为了验证此控制方法的性能，以某伺服阀控制系统为例在MATLAB/ SIMULINK下进行了仿真。各项取值参考如下：ωsv=590 rad/s，ξsv=0.7，Ksv=0.003 1 m3/s·A，Kce=11.6×10-10m5/(N·s)，AP=1.9×10-4m2，Vt=1.4×10-3m3，βe=0.9e+9 (Pa)，Kd=1.29，ωn=22.8 rad/s，ξn=0.2，Kq=1.88。

首先验证本文所提控制器在无扰动情况下的控制效果，仿真结果如图5所示。

图5 无负载时的系统响应

由图5可知，若主通道控制器为常规模糊控制器，在没有负载输入的情况下，输入单位阶跃响应信号，则在系统稳定以后，有稳态误差的存在；而采用自调整模糊控制器，无论是否加入前馈环节，稳态误差均基本消除，同时在系统相应速度与超调量上还有优势。

在系统有扰动下的情况，假定负载由0～3000 N和0～7000 N两种情况进行交替变化，考虑到在交替变化的过程中存在一些不确定的扰动，因此，在变化曲线中加入一定幅度的白噪声信号以模拟不确定扰动。负载变化曲线如图6所示，控制效果如图7所示。图中加入前馈的自调整因子模糊控制器的控制效果，无论是在相应速度、超调、鲁棒性等指标上均优于另两种控制。

模拟现场控制的实际情况，如需液压阀的位移量为5.5 cm，则三种方法所得的实际结果如图8所示，本文所提方法的控制效果令人满意。

图6 输入负载

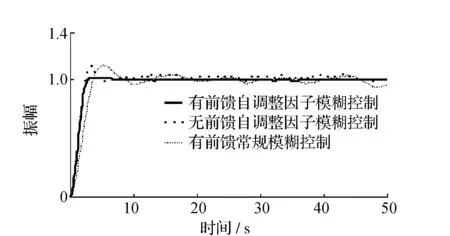
图7 有负载扰动时的系统响应

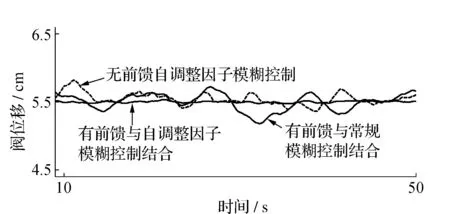
图8 模拟现场控制效果

4 结束语

本文通过建立伺服系统的控制模型，分析了系统负载存在的不确定性和扰动性，提出了前馈与自调整因子相结合的液压阀控伺服系统的跟踪控制方案。仿真结果表明，结合前馈的自调整因子模糊控制应用于阀控伺服系统中，使系统的稳定性和控制精度得到了明显的改善，并使控制系统具有了较强的鲁棒性。

[1] LIU G P, DALEY S. Optimal-tuning Nonlinear PID Control of Hydraulic System [J].Control Engineering Practice,2000,8(9)：1045-1053.

[2] 王燕山,王益群.基于QFT的电液力伺服系统的鲁棒控制[J].中国机械工程,2003,14(9)：731-733.

[3] 段锁林,安高成,薛军娥,等.电液伺服力控系统的自适应滑模控制[J].机械工程学报,2002,38(5):109-112.

[4] 韩俊伟,赵慧,马剑文,等.具有时变柔性负载的电液力控制系统中Gain-scheduled H∞鲁棒控制器的研究[J].机械工程学报,2000,36(4):58-61.

[5] 李洪人．液压控制系统[M]．北京：国防工业出版社，1981.

[6] TAN W W, DEXTER A L. A Self-learning Fuzzy Controller for Embedded Application[J].Automatic,2000,36：1189-1198.

[7] LI Yan-peng，LI Xiang, ZHUANG Zhao-wen. Target identification effect evaluation based on choquet fuzzy integral[J].Journal of Systematic Imitation,2005,17(5):695-699.

[8] WANG Xi-zhao, CHEN Jun-fen. Multiple neural networks fusion model based on choquet fuzzy integral[C]. Proceedings of the Third International Conference on Machine Learning and Cybernetics. Shanghai, 2004,4,2024-2027.

[9] 邢宗义，张媛，侯远龙,等.电液伺服系统的建模方法研究与应用[J].系统仿真学报，2009,21(6):1719-1725.

[10] 于浩洋,关广丰，于笑平，等.电液振动台加速度波形再现控制算法[J].黑龙江工程学院学报：自然科学版，2013，27(1)：60-63.

[责任编辑：郝丽英]

Feed forward and fuzzy control with rule of self-adjusting factors on hydraulic valve-control system

YU Hao-yang

(College of Electronic and Information Engineering, Heilongjiang Institute of Technology, Harbin 150050, China)

Based on the uncertainty and disturbance in hydraulic valve-control system of load, the mathematical model of hydraulic valve-control system is set up, the control method of feed forward fuzzy control with rule of self-adjusting factors is designed, the control principle of the controller is analyzed, the basic structure of the controller is designed, and the simulation is done on the environment of MATLAB /SIMULINK in order to verify this method. The simulated results indicate that the fuzzy control with rule of self-adjusting factors combined with control of the feed forward can get better control effect in using hydraulic valve-control system.

feed forward; self-adjusting factor; hydraulic valve-control system; interference of extra load; simulation

2014-08-17

黑龙江省教育厅基金资助项目(12521447)

于浩洋(1968-)，男，副教授，研究方向：智能控制及仿真.

TP271.31

A

1671-4679(2015)02-0018-04