基于理想视线制导的多导弹协同攻击策略
李 浩,毛昱天,吴 丹,杨 明
(中国兵器工业导航与控制技术研究所,北京100089)
基于理想视线制导的多导弹协同攻击策略
李 浩,毛昱天,吴 丹,杨 明
(中国兵器工业导航与控制技术研究所,北京100089)
理想视线制导律是一种沿理想视线方向的、对终端相对位置与终端相对速度进行控制的弹道成型制导律。基于此制导律,提出了一种圆弧假设并推导了理想视线约束角度与飞行剩余时间之间的函数关系,设计了多导弹飞行时间协同控制系统。在此基础上,提出了针对低速目标的多导弹协同攻击策略。该制导策略通过调节各导弹终端理想视线与相对距离矢量方向夹角大小的方法,有效地减小了各导弹飞行时间之间的差额。仿真结果表明,所设计的制导策略可以很好地实现多导弹对固定目标的协同攻击并且有较强的容错性。
协同制导;攻击时间控制;弹道成型;最优控制
0 引言
随着现代战争的发展,近防武器系统 (Closein Weapon System)在舰船系统中愈发普及,这使得传统反舰导弹的适用性受到了威胁。除了提高导弹单体性能之外,多导弹协同攻击制导策略也是重要的研究方向之一。多导弹可以在时间上实现饱和攻击,极大提高突防的可能性。同时,基于多视线观测原理[1],多枚红外制导导弹同样可以对目标进行精确定位,为现代制导律的应用提供了更多可能性。
目前主流的时间协同攻击制导律可以分为两类:多导弹间不存在/存在信息交互。前者由文献[2]首次提出,在传统的最优制导控制回路基础上加入了新的时间控制回路,设计了飞行时间可控制导律 (ITCG)。利用当前剩余飞行时间与预先设定剩余时间的差值,对总的弹道长度进行再规划,以实现同时攻击的目的。文献 [3]在文献[2]的基础上,加入了末端的弹道角约束回路,能够实现时间与方向上的协同攻击 (ITACG)。在文献 [2-3]中没有考虑导弹之间存在通信,因此必须在发射前设定统一着弹时间,且设定的统一着弹时间必须大于每枚导弹的着弹时间。当与所设时间点有较大偏差时,制导系统会受到较大的不良影响。考虑到这一因素的影响,文献 [4]在导弹之间存在通信的情况下,基于比例制导律设计了协同比例制导率 (CPN),其中每枚导弹的比例制导系数为根据自身飞行剩余时间与其他飞行器飞行剩余时间变化的时变函数。不同的制导系数会对剩余的飞行时间有不同的影响,进而实现多导弹协同攻击的目的。CPN是一种针对低速目标的强实用性协同制导策略,但比例制导系数N对飞行剩余时间的有效影响是建立在导弹发射时具有较大前置角偏差的基础上的,而当前置角偏差较小时,制导律将不能有效地减小多导弹剩余时间的差额。文献 [5]在文献 [4]的基础上利用最优控制理论,基于零效脱靶量推导了时间协同制导律,但同样具有相同的问题。协同制导攻击方面的研究有很多,但重点在时间协同的相对较少,对于其他方面的研究内容,这里不再一一列举。
弹道成型制导律是一种通常设定终端的约束视线对弹道进行再规划的制导策略,不同的终端约束视线会对弹道轨迹有不同的影响。关于弹道成型制导律有非常多的研究成果,主要可以分为基于最优控制理论和基于传统比例制导两大类。前者在文献 [6]中首次提出,研究侧重于终端姿态角约束条件下的线性制导系统的最优控制。文献 [7]提出了弹道轨迹可预测条件下的机动目标攻击使用的弹道角约束最优制导律。文献 [8]利用最优控制理论推导了存在动力学滞后时的末端弹道成型制导律,可以满足期望的终端攻击要求。文献 [9]在最优控制理论和微分对策理论 (differential game methodology)的基础上,利用零效脱靶量概念推导了末端弹道成型制导律,在目标机动和较大前置角误差的情况下,仍具有良好的性能。理想视线弹道成型制导律[10-11]是一种基于最优控制理论,控制目的为使弹目相对距离和相对速度矢量方向沿所设定终端理想视线方向的弹道成型制导律,结构简单,方便应用。
本文基于理想视线弹道成型制导律,设计了多导弹协同攻击制导策略,通过调节终端理想视线与当前弹目视线的夹角qL以实现对飞行剩余时间的控制,而qL的大小由导弹自身飞行剩余时间与多导弹剩余时间均值的差额所决定。当飞行剩余时间大于均值时,增大qL;反之,减小qL。
文章结构安排如下:第一节,理想视线弹道成型制导律的推导;第二节,飞行时间控制系统设计;最后,仿真并对数据进行分析。
1 制导律推导
为了使模型简化,便于线性二次型控制理论的应用,作如下假设:
1)导弹和目标均看作质点运动;
2)导弹和目标的绝对速度为常值;
3)制导系统是理想的,即制导系统没有延迟。
在二维情况下,导弹和目标的相对运动关系如图1所示。

图1 弹目相对运动示意图Fig.1 Guidance geometry on one-to-one engagement scenario
图1中:OXY——惯性坐标系,以发射时刻导弹位置为原点,X 轴为发射时刻视线在水平面上的投影,Y轴沿高度方向;
Mi——第i枚导弹的位置;
T——目标的位置;
RTMi——第i枚导弹的弹目相对距离;
VMi——第i枚导弹的弹目相对速度;
RTMi⊥——RTMi在垂直于Li方向上的投影;
VMi⊥——VMi在垂直于Li方向上的投影;
Li——第i枚导弹所设的理想视线;
qL——所设的理想视线与当前相对距离的夹角。
在下文中为了符号简化,将不再对导弹序号进行标注。
根据图1可以建立垂直于理想视线的弹目相对运动学方程
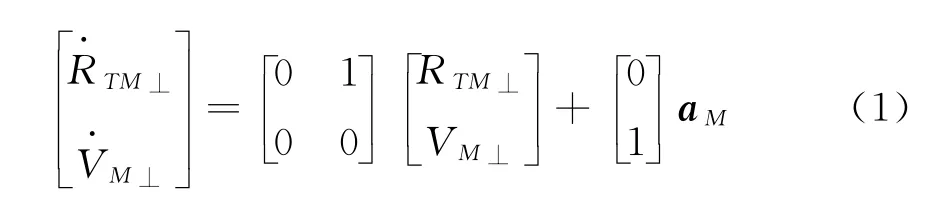
其中aM为导弹垂直于Li方向的需用加速度。
设:x1=RTM⊥,x2=VM⊥
则可建立垂直于L方向的弹目相对运动方程如下

利用最优控制理论对制导律进行推导,控制目的为终端时刻弹目相对位置和相对速度与理想视线L方向相同,即要求x1(tf)和x2(tf)为零且能量最优,所以选取能量函数如式 (3)所示
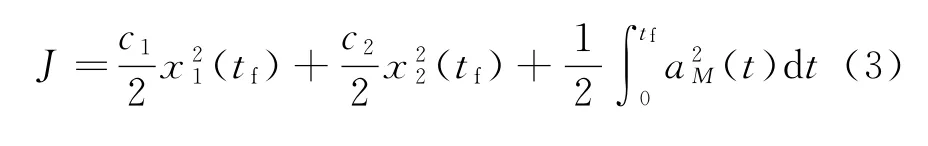
式 (3)中,c1、c2为终端状态加权系数,tf为终端时间。构造哈密顿函数


构造伴随方程:
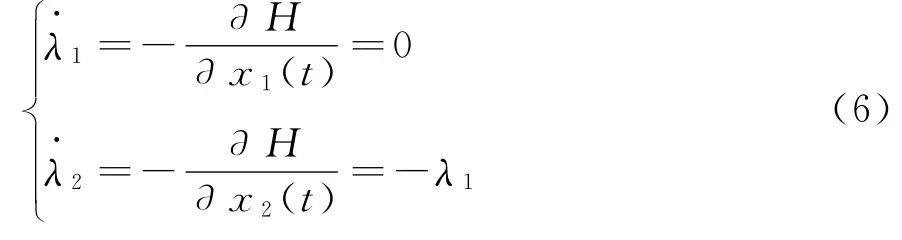
边界条件为

由式 (6)~式 (7)可以解出λ1(t)和λ2(t)
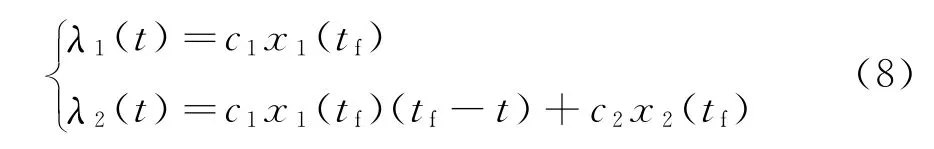
将式 (8)代入式 (5)可以得出

将式 (9)代入状态方程,并从t到tf积分,可将aM改写为

其中:

从式 (10)可以看出,aM(t)是待定常数c1、c2的函数。c1、c2选择不同的值,可以得到不同的制导律。因要求导弹终端状态x1(tf)和x2(tf)都尽可能小,故选择c1→∞,c2→∞,并将其代入式(10),可得式(12)

其中tgo为剩余飞行时间。这与采用经典的弹道成型制导律形式是相似的,但其中参数变量的物理意义是不同的。
2 飞行时间控制系统设计
理想视线制导律通过设定理想视线的方向角,对飞行弹道轨迹进行再规划,使末端弹目视线满足约束条件。在初始相对距离及导弹轴向速度一定时,设理想视线与初始相对距离的夹角qL作为终端约束条件,对整体的弹道轨迹长度有明显的影响,另一主要的影响因素为速度初始前置角偏差θ0,因此可以从这两个主要影响因素入手,对飞行时间进行分析,并设计飞行时间控制系统。
2.1 飞行时间仿真分析
在二维非线性环境下进行数字仿真,设导弹初始位置为(0,0),速度为300m/s,目标位置为(1000,0),速度为0m/s,采用理想视线制导律进行制导。仿真结果飞行时间tF与终端夹角qL的关系如图2,可以看出qL的大小对tF有明显的影响,而θ0在较小的情况下对tF的影响不大,可以忽略不计。在此基础上,可以利用圆弧弹道估计法对不同qL约束下的弹道轨迹与飞行总时间进行估计。

图2 飞行时间tF与qL关系图Fig.2 Simulation analyses about time-to-go
2.2 圆弧弹道估计算法
理想视线制导律的飞行轨迹为类圆弧曲线,考虑到其制导律形式的复杂程度,很难写出其弹道的解析表达式,但可以利用圆弧长度对不同qL约束下的剩余弹道长度近似计算,计算原理如图3所示,RTM0为当前弹目相对距离,M0为导弹当前位置,T0为目标位置,当理想视线与当前弹目相对距离夹角大小为qL时,RTM*为剩余弹道轨迹长度的估值,其大小等于以OM0、OT0为半径的圆所对应的弧长。
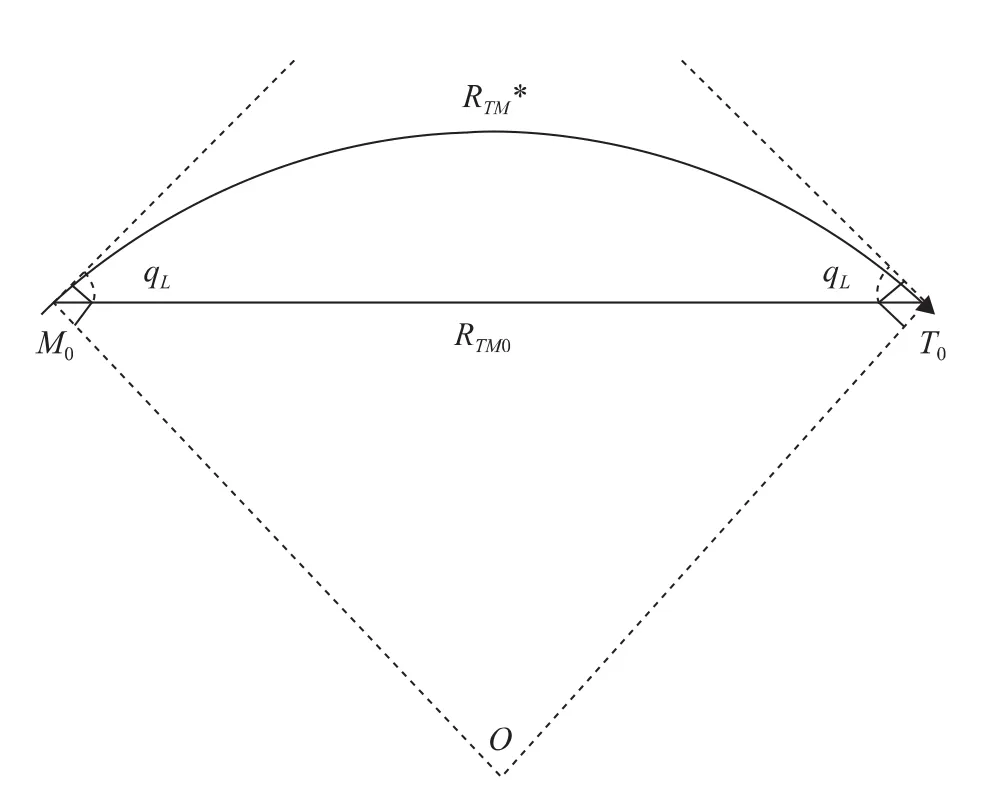
图3 圆弧法轨迹估计原理图Fig.3 Arc hypothesis about the time-to-go

在小扰动假设的基础上,以某一静态工作点qL0为例,对式 (13)进行线性化,得到t*F与qL在qL0附近的线性关系式:

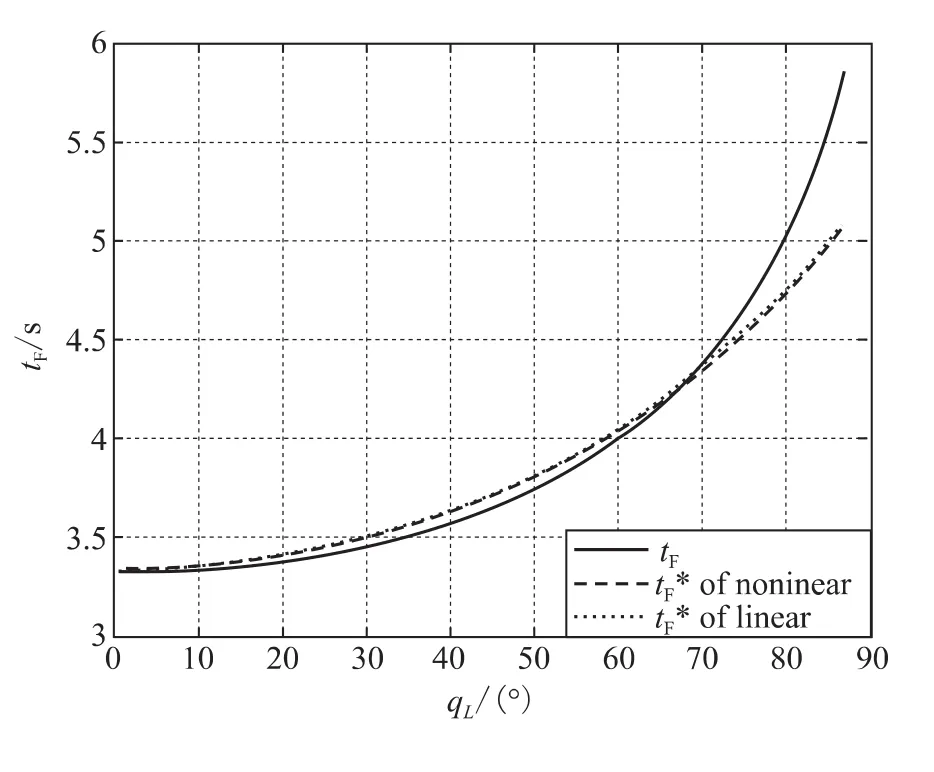
图4 圆弧法估值结果分析Fig.4 Performance of the new estimation method in time-to-go
2.3 飞行控制系统设计
由上文中的分析结果及式 (14)可以看出,在前置角误差较小的情况下,导弹在飞行中某一时刻对应的剩余飞行时间,是由终端理想视线与当前相对距离的夹角qL与最短飞行时间tF0决定的。在此基础上,以三导弹对一目标为例,设计了协同攻击时间控制系统,如图5所示。系统的输入为上一时刻多系统输出的均值,导弹控制系统中的增益系数K1、K2、tF0分别由各自的飞行状态决定。

图5 飞行时间控制系统示意图Fig.5 Impact-time control system
3 仿真结果分析
针对所设计的制导律及飞行时间控制系统,以三导弹对一目标为例,完成了二维平面内的数字仿真验证。导弹的初始位置分别为:(-1000,0),(0,0),(0,1000m);导弹速度为500m/s;速度前置角误差分别为:0°,45°,0°;目标位置为(20000,0)。仿真结果如图6、图7和图8所示。图6表明,在导弹初始位置不同,初始飞行剩余时间有较大差距的情况下,制导策略能够完成多导弹对目标的协同攻击任务,并且对初始速度前置角并不敏感。从图7可以看出,时间控制系统可以有效地减小导弹飞行剩余时间之间的误差,实现协同攻击的目的。图8为各枚导弹的需用过载曲线图。

图6 多导弹协同攻击弹道曲线Fig.6 Flight trajectories for missiles

图7 导弹剩余飞行时间图Fig.7 Time-to-go histories

图8 导弹需用过载图Fig.8 The required acceleration of missiles
4 总结
本文就理想视线弹道成型制导律,设计了一种多导弹时间协同制导策略,并以三导弹对一目标为例,进行了数字仿真验证。仿真结果表明:该制导策略能够准确地实现针对固定及低速目标的协同攻击制导任务,并且对速度初始前置角无具体要求,是一种实用性较强的多导弹协同攻击策略。
[1]Zarchan P.Kill vehicle guidance and control sizing for boostphase intercept[J].Journal of Guidance,Control,and Dynamics,2011,34(2):122-127.
[2]Jeon I S,Lee J I,Tahk M J.Impact-time-control guidance law for anti-ship missiles[J].IEEE Transactions on Control Systems Technology,2010,14(2):260-266.
[3]Lee J I,Jeon I S,Tahk M J.Guidance law to control impact time and angle[J].IEEE Transactions on Aerospace and E-lectronic Systems,2007,43(1):301-310.
[4]Lee J I,Jeon I S,Tahk M J.Homing guidance law for cooperative attack of multiple missiles[J].Journal of Guidance,Control,and Dynamics,2010,33(1):275-280.
[5]Sun X,Xia Y.Optimal guidance law for cooperative attack of multiple missiles based on optimal control theory[J].International Journal of Control,2012,85(8):1063-1070.
[6]Kim M,Grider K V.Terminal guidance for impact attitude angle constrained flight trajectories[J].IEEE Transactions on Aerospace and Electronic Systems,1973,9(6):852-859.
[7]Idan M,Golan O M,M Guelman.Optimal planar interception with terminal constraint[J].Journal of Guidance,Control,and Dynamics,1995,18(6):1078-1083.
[8]Song T L,Shin S J,Cho H.Impact angle control for planar engagements[J].IEEE Transactions on Aerospace and Electronic Systems,2008,35(4):1439-1444.
[9]Paul Z.Tactical and strategic missile guidance[M].2008.
[10]Shaferman V,Shima T.Linear quadratic guidance laws for imposing a terminal intercept angle[J].Journal of Guidance,Control,and Dynamics,2008,31(5):76-85.
[11]李浩,佘浩平.基于理想视线的弹道成型最优导引律[J].兵工学报,2014,8(2):102-113.
Cooperative Attack of Multiple Missiles with Ideal-line-of-sight-guidance
LI Hao,MAO Yu-tian,WU Dan,YANG Ming
(Chinese Ordnance Navigation and Control Technology Research Institute,Beiijng 10089,China)
Ideal-line-of-sight-guidance is a trajectory shaping guidance law which makes the vector of relative positions and velocity the same direction as ideal-line-of-sight.This paper builds formulas about the direction of idealline-of-sight and time-to-go by supposing the constrained trajectory a circular arc,and the impact-time control system for multi-missile is designed by the formulas.Based on the above study,a new guidance scheme of cooperative attack is proposed,which can be applied to salvo attack of anti-ship missiles.The new guidance scheme can extremely reduce the difference in time-to-go between each missile by adjusting the included angle between ideal-lineof-sight and the vector of relative positions.Numerical simulations demonstrate the performance of the proposed guidance scheme in the accuracy of impact time and high robustness.
Cooperative guidance;Impact-time control;Trajectory shaping;Optimal control
TP273
A
2095-8110(2015)04-0001-06
2015-05-07;
2015-05-21。
李浩 (1990-),男,硕士,主要从事飞行器导航制导与控制方面的研究。
- 导航定位与授时的其它文章
- 空间三轴激光陀螺稳频方法研究

