多次反射对垂直磁偶极子的场强影响
张立琛 王英民 郭 拓
(西北工业大学航海学院 西安 710072)
0 引 言
电磁场在半空间或分层媒质中是如何辐射和传播的,一直受到人们极大的关注,这是因为它在实际工程领域甚至军事应用方面有着重要的意义和广泛的前景.水下通信[1-3]、地球物理勘探[4]、潜艇探测和通信[5]等领域都会遇到类似的问题.对于实际应用中的数学模型的建立,何种形式的偶极子模型更加接近实际情况,一直是研究的热点和难点[6].
海底通信在人类活动中早已存在,很多情况下人们利用环天线进行海水中的通信联络,因此研究海水中环天线的辐射电磁场是非常重要的.Moore[7]在假定海水是无限深的情况下讨论了2层导电媒质(空气、海水)中环天线的辐射问题,这在海水较深或电磁波频率较高时是适宜的.卢新城[8]推导出极低频时谐水平电偶极子在海水中(2层导电媒质)所产生电磁场的近似解析表达式,这在海水较深情况下(不用考虑海底影响)较为适宜.当研究浅海环境中极低频偶极子天线的辐射问题时,需要考虑海底的影响,这时偶极子天线位于3层导电媒质(空气、海水、海底)中.最早是由Arutaki[9]推导出了3层导电媒质中环天线在海水中的远区场强公式,该方法涉及到数次积分变换和积分路径的变换,而且积分的最速下降路径越过了支割线,必须计算支点对总场的贡献,公式推导繁杂、冗长.龙云亮[10]在 Chew[11]的基础上用一种新的远场近似方法得到了垂直磁偶极子在海水和空气中的电磁场表达式,但其研究是基于无穷远的条件下,对于极低频电磁波,由于其波长很大,在无穷远情况下电磁波信号很难被接收到,同时其认为海底反射影响很小,直接忽略海底部分,对于靠近海面情况下,可以近似忽略,对于浅海环境中,当靠近海底情况时,海底影响不能被忽略.
镜像法是根据惟一性原理求解某些具有导体边界的电磁场边值问题的一种经典方法[12].本文将其用于3层导电媒质中,对空气-海水-海床3层媒质组成的环境下海水中的极低频垂直磁偶极子在海水中产生的电磁场进行了推导,由此得到海水中极低频电磁场分布的解析表达式,该方法推导得到的解析表达式能够清晰的表达出电磁波在海水中的传播路径,通过仿真计算和分析,表明远场情况下,海面和海底之间的多次反射波对总场场强的贡献很小,可忽略不计;对总场场强起主要作用的传播路径为:从场源发出以最小距离到达最近分界面经一次反射直接到达接收点.
1 三层媒质模型
所研究问题的物理模型见图1.
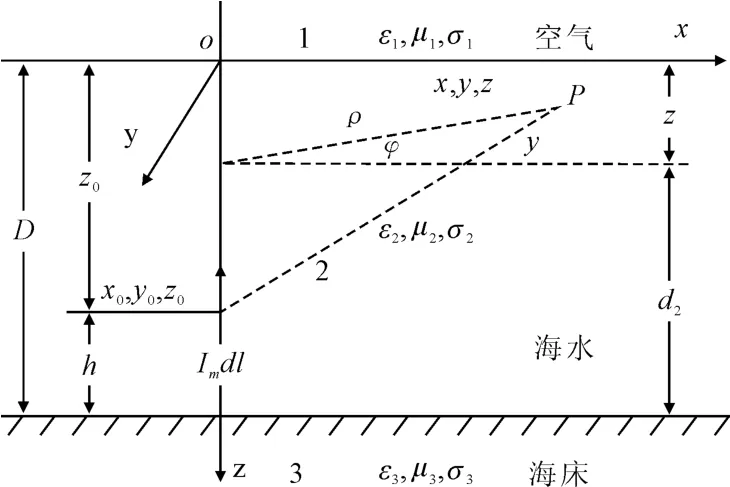
图1 3层媒质中的垂直磁偶极子
全空间被z=0和z=D2个平面分成3个部分,其中z=0为空气和海水分界面;z=D为海底平面.分成的3个区域分别为:1-空气;2-海水;3-海床,对应媒质的电容率、磁导率及电导率分别为(εi,μi,σi),i=1,2,3.建立直角坐标系,以垂直于海平面向下为z轴正向,可设磁偶极子Imdl位于(x0,y0,z0)处,0<z0<D,即磁偶极子源位于海水区域中,场点坐标为(x,y,z),0≤z≤D,则表示场点也位于海水区域中.垂直磁偶极子Imdl平行于z轴,图1中所示为3层媒质中的垂直磁偶极子,下文以垂直磁偶极子为例进行推导.
2 三层模型中镜像法的应用
推导偶极子模型产生的电磁场公式,既可以通过矢量位方法求得,也可以用傅里叶变换方法推导,也可以通过波动方程方法求得.但是,用矢量位方法求电磁场,物理意义更明显,公式推导更方便.所以,越来越多的学者采用该方法推导电磁场解析表达式,本文也采用该方法推导垂直磁偶极子在3层媒质中的电磁场的解析表达式.
2.1 2层媒质(空气、海水)
如图2所示,只考虑存在空气、海水2层媒质,由于垂直磁偶极子源位于区域2(海水媒质中)内,因此,垂直矢量电位满足非齐次标量亥姆霍兹方程[13],即
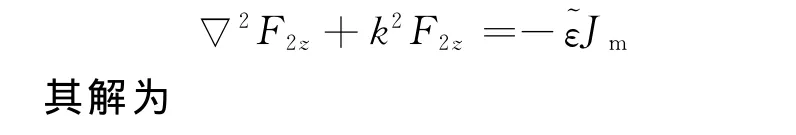
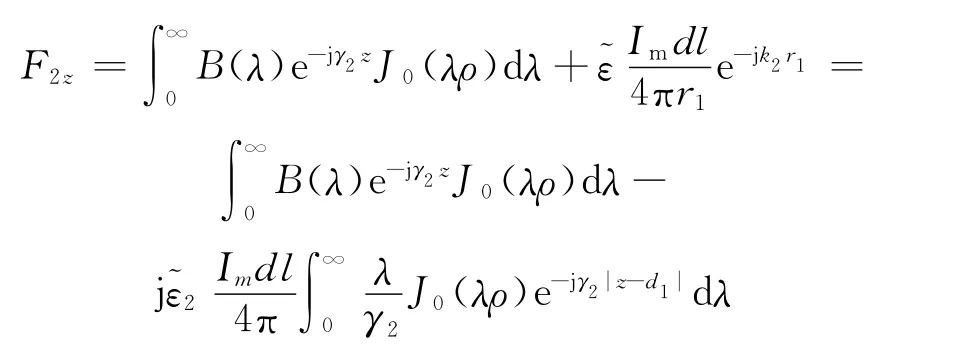
若场点位于海水中,即z≥0,则由镜像法可设像I′mdl位于(x0,y0,-z0),全空间视为充满海水,式即为源和像共同在场点产生的矢量电位.第二项是非齐次标量亥姆霍兹方程的特解,代表电磁场源发射的球面波,即为源在场点产生的矢量电位;第一项是齐次标量亥姆霍兹方程的通解,可用分离变量法求出,即为像在场点产生的矢量电位.由于垂直偶极子的旋转对称性,通解与方位角无关.通解实际上代表的是边界的反射波,它表示为无穷多不均匀平面波的合成.在区域1内,不存在任何场源,所以垂直矢量电位满足齐次标量亥姆霍兹方程,即

把式(2),(4)代入式(5)得到区域2内源和像共同在场点产生的矢量电位的表达式为
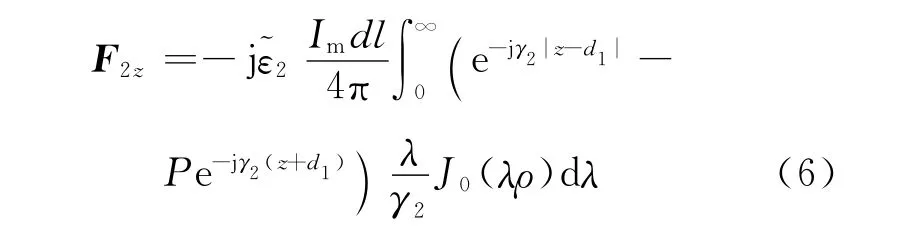
式中:M=γ1+γ2;P=(γ1-γ2)/M.第一项是场源(垂直磁偶极子)产生的矢量电位,第二项是像(即界面反射)产生的矢量电位.-P可以看作是界面(空气-海水)对不均匀平面波谱的反射系数.
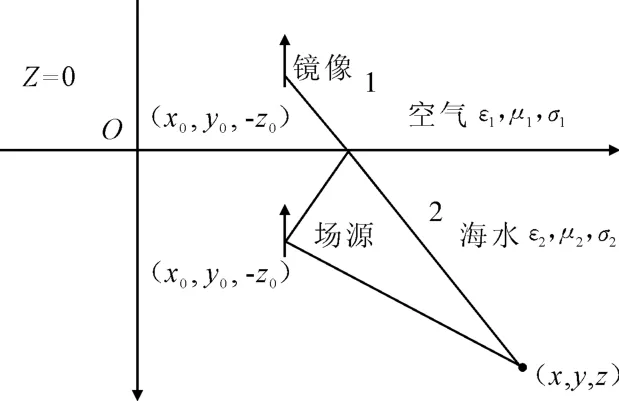
图2 镜像法求2层媒质(空气-海水)时海水中的场
2.2 三层媒质(海水、海床)
只考虑存在海水、海床2层媒质,同理,2.1中的分析可知,区域2内源和像共同在场点产生的矢量电位的表达式为
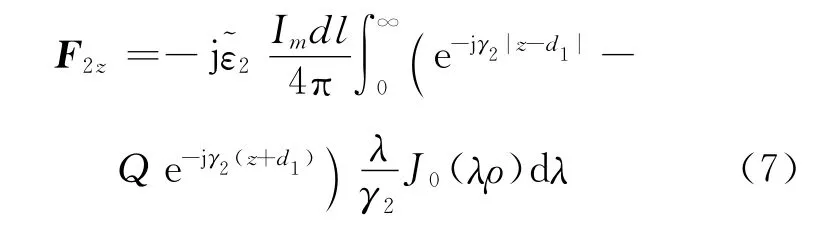
式中:N=γ2+γ3;Q=(γ3-γ2)/N.第一项是场源(垂直磁偶极子)产生的矢量电位,第二项是界面反射引起的矢量电位.-Q可以看作是界面(海水-海底)对不均匀平面波谱的反射系数.
2.3 三层媒质(空气、海水、海床)
当存在2个平行分界面时,磁偶极子在2个界面之间不断“镜像”,因此在图1所示的海水模型中,位于海水中一个垂直磁偶极子在海水中的场点处产生的场可以用图3所示的无穷多个镜像垂直磁偶极子在无限大的海水空间分别产生的场的叠加来替代.
通过上面分析可知,P和Q分别是2个分界面的反射系数,那么对于图中场源和所有镜像源,相对应的矢量电位表达式为
1)场源,位置 (x0,y0,z0);传播路径:场源直接到场点;矢量电位表达式:e-jγ2|z-z0|.
2)镜像1,位置 (x0,y0,-z0);传播路径:从场源经z=0界面反射后到达场点;矢量电位表达式:-.
3)镜像2,位置 (x0,y0,2D-z0);传播路径:从场源经z=D界面反射后到达场点;矢量电位表达式:-.
4)镜像3,位置 (x0,y0,-2D+z0);传播路径:从场源先经z=D界面反射,再经z=0界面反射后到达场点; 矢量电位表达式:.
5)镜像4,位置 (x0,y0,2D+z0);传播路径:从场源先经z=0界面反射,再经z=D界面反射后到达场点;矢量电位表达式:.
6)镜像5,位置 (x0,y0,-2D-z0);传播路径:从场源先经z=0界面反射,再经z=D界面反射,再经z=0界面反射后到达场点;矢量电位表达式:-.
上面只是给出了场源和5个镜像的具体分析,通过观察规律,对比分析,可将磁偶极子及其所有的镜像划分为以下4类.
1)位置 (x0,y0,-2mD+z0) 矢量电位表达式:(PQ
2)位置 (x0,y0,-2mD-z0) 矢量电位表达式:(-P)m+1(-Q
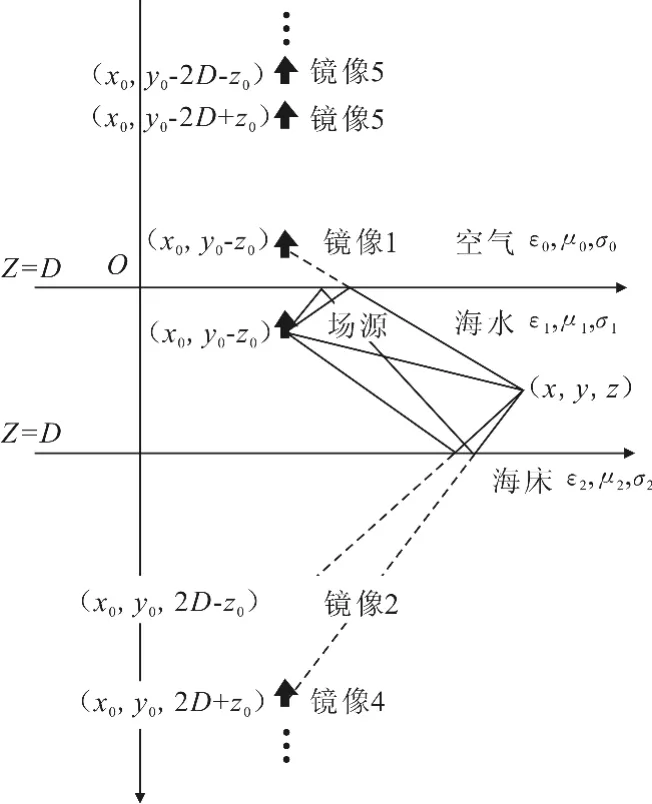
图3 3层媒质时的垂直磁偶极子的镜像
3)位置 (x0,y0,2nD +z0) 矢量电位表达式:
4)位置 (x0,y0,2nD -z0) 矢量电位表达式:(
式中:m =0,1,2,…;n=1,2,… .
因此,3层媒质中,区域2内的垂直矢量电位的表达式为

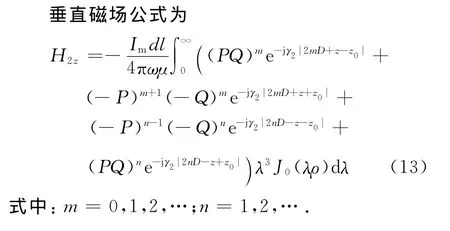
3 仿真实验
由于各个分量有其明确的物理意义,即分别代表不同的传播路径,因此可以通过仿真分析各个传播路径对总场强度的影响.本文对式(11)~(13)中的积分采用高斯勒让德数值积分的方法来求解,在不追求算法速度的条件下,该方法计算过程简单且结果足够精确.
仿真条件:垂直磁偶极子的磁偶极矩Imdl=10A·m2,频率为3Hz,海水的深度为a,场源深度为d1,接收点深度为z,垂直磁偶极子在水下姿态如图1所示.空气电导率σ1=0,海水电导率σ2=4Ω/m,海底电导率σ3=4×10-2Ω/m,空气介电常数ε1=8.85×10-12F/m,海水介电常数ε2=81ε1,海底介电常数ε2=8ε1,各层媒质的磁导率均为真空磁导率.数值计算结果见图4~7.
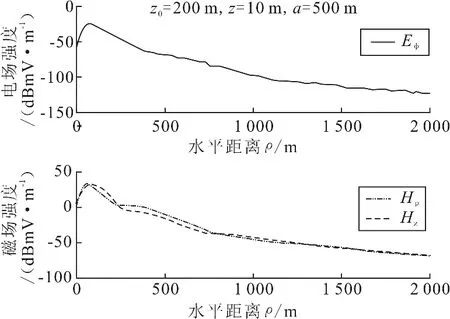
图4 3个总场随水平距离变化
图4 是场源深度200m、接收点深度10m、海水深度500m时对电磁场(垂直磁偶极子)3个总场的场强强度对比,显而易见,3个总场的场强衰减趋势大体一致,近距离时衰减很快,随着距离的增加,衰减速度慢慢变缓,当水平距离为2 000m时,Eφ分量的电场强度为-122dBmV/m,Hρ分量和Hz分量的磁场强度一样,都为-69.83 dBmA/m.
由于3个总场的规律相似,鉴于篇幅限制,这里仅以Eφ电场分析对比,给出变化规律.下面几幅仿真图验证不同传播路径对总长场强的影响.在图中海面即为电磁波经过z=0分界面(空气-海水)反射,海底即为电磁波经过z=D分界面(海水-海床)反射,括号里面的数值代表经过几次反射.例如镜像5的传播路径为从场源先经z=0界面反射,再经z=D界面反射,再经z=0界面反射后到达场点,其表达形式为海面(2)、海底(1).
图5是场源深度200m、接收点深度10m、海水深度500m时对电场Eφ分量的多次反射传播路径的仿真对比.从图中可以看出,同一种颜色表达的两种传播路径的差别在于相差一次海面反射和海底反射,对比可知,在远场情况下,增加一次海面海底之间反射,到达接收点的场强相比要小很多.其原因是由于电磁波在导电的海水中传播时激起了传导电流,致使电磁波的部分能量转化为热能被海水吸收,从而使得传播途中出现能量衰减,且传播越远,衰减越大,频率越高,衰减越快,界面间一次反射已经很小,对场强贡献可忽略不计,因此,多次反射的传播路径会更小,可忽略不计.下面几幅图将分析场源和场点位置不同时,不同传播路径对总场场强的贡献.
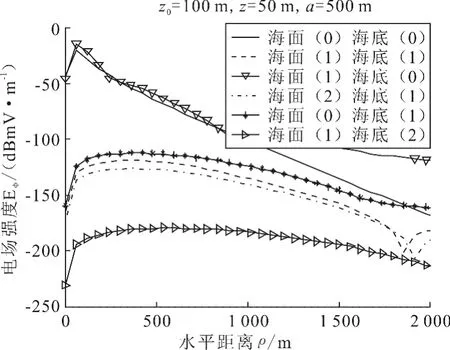
图5 多次反射对Eφ场场强的贡献
图6 和图7是海深500m时场源和接收点分别靠近海面(场源深度20m、接收点深度5m)和靠近海底(场源深度480m、接收点深度495m)时不同传播路径对E(场场强的贡献.由前面仿真分析已知,海面海底间多次反射对于总场场强贡献可忽略不计,因此,这里仿真直接忽略了海面海底之间的相互作用(海面海底之间反射次数大于1),直接给出只经海面或海底1次反射的传播路径.可以看出,在远场情况下,离海面近时,经海面反射直接到达接收点的传播路径的场强曲线与总场场强曲线重合,其他几条传播路径对总场场强贡献可忽略不计;离海底近时,经海底反射直接到达接收点的传播路径的场强曲线与总场场强曲线重合,其他几条传播路径贡献可忽略不计.
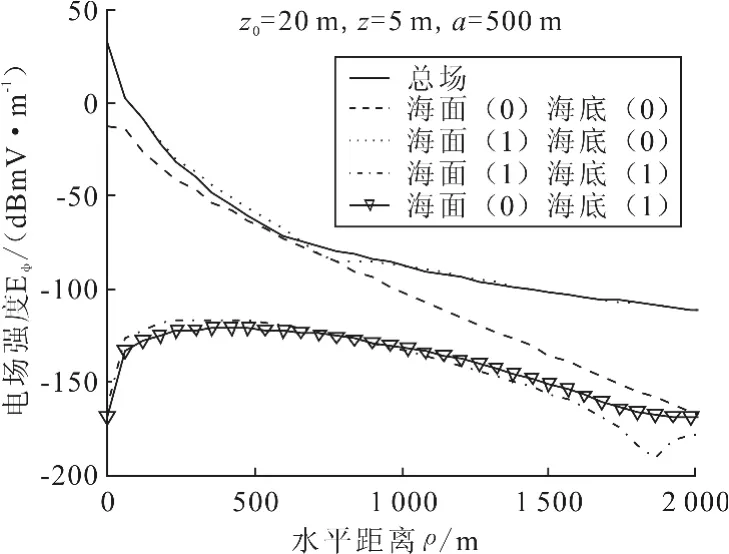
图6 场源和场点靠近海面时不同传播路径对Eφ场场强的贡献
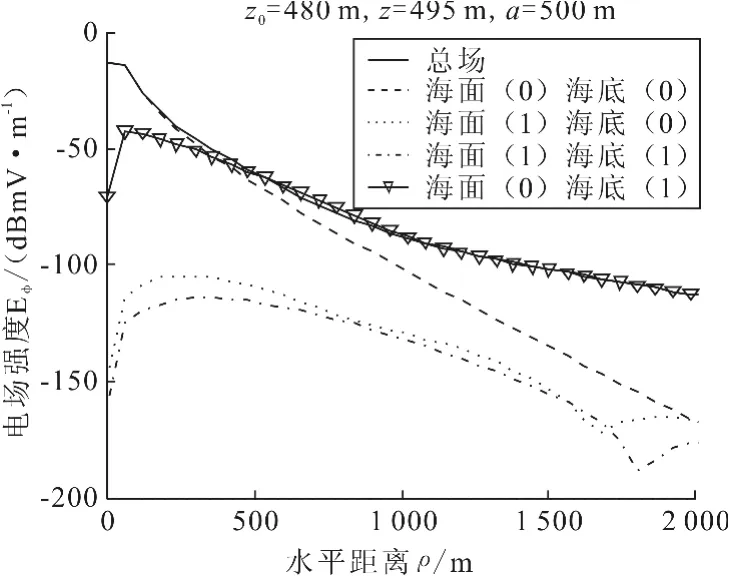
图7 场源和场点靠近海底时不同传播路径对Eφ场场强的贡献
上述仿真结果表明,在远场情况下,对总场场强起主要作用的传播路径为:从场源发出以最小距离到达最近分界面经一次反射直接到达接收点.
4 结 论
本文利用镜像法,在空气-海水-海床三层模型下,在电磁场惟一性原理的基础上,通过矢量电位方法推导了垂直磁偶极子在海水中产生的电磁场的解析表达式.通过该方法推导出的电磁波表达式各个分量有明确的物理意义,且推导过程更加简单.通过对各个分量仿真的结果可以得出以下几个结论.
1)通过该方法推导得到的电磁波表达式能够清晰的表达电磁波在海水中的各个传播路径,这样,可以分别对每个传播路径进行仿真,分析其对总场场强的影响;
2)在远场情况下,由于电磁波在导电的海水中传播时激起了传导电流,致使电磁波的部分能量转化为热能被海水吸收,因此,海面和海底之间的多次反射波对总场场强的贡献可忽略不计;
3)在远场情况下,对总场场强起主要作用的传播路径为:从场源发出以最小距离到达最近分界面经一次反射直接到达接收点.
[1]ARUTAKI A,CHIBA J.Communication in a threelayered conducting media with a vertical magnetic dipole[J].Antennas and Propagation,IEEE Transactions on,1980,28(4):551-556.
[2]URIBE C,GROE W.Radio communication model for underwater WSN,in New Technologies[C].Mobility and Security (NTMS),2009 3rd International Conference,2009.
[3]GOHB J H.Underwater wireless comm-unication system [J].Journal of Physics:Conference Series,2009,178(1):12-29.
[4]LONG Yunliang,JIANG Hongyan.Electromagnetic field due to a loop antenna in a bore hole[J].Geoscience and Remote Sensing,IEEE Transactions,1996,34(1):33-35.
[5]RHODES M.Electromagnetic propagation in sea water and its value in military systems[C].SEAS DTC Technical Conference,2007.
[6]陈 聪,李定国,龚沈光.舰船水下标量电位的混合建模研究[J].武汉理工大学学报:交通科学与工程版,2010,34(6):1117-1120.
[7]MOORE R K.Dipole radiation in a conducting half space[J].J.Res.Natl.Bur.Stand.,1961,28:515-522.
[8]卢新诚,龚沈光,周 骏,等.海水中极低频水平电偶极子电磁场的解析解[J].电波科学学报,2004,19(3):290-295.
[9]ARUTAKI A.Communication in a three-layered conducting media with a vertical magnetic dipole[J].IEEE Transactions on Antennas and Propagation,1980,28(4):551-556.
[10]LONG Yunliang,JIANG Hongyan.Bernhard rembold far-region electromagnetic radiation with a certical magnetic dipole in sea[J].IEEE Transactions on Antennas and Propagation,2001,49(6):992-996.
[11]CHEW W.A quick way to approximate a Sommerfeld-Weyl-type integral[J].IEEE Transactions on Antennas and Propagation,1988,36:1654-1657.
[12]陈 聪,李定国,龚沈光.浅海中静态电偶极子电场分布的镜像法研究[J].武汉理工大学学报:交通科学与工程版,2010,34(4):716-720.
[13]袁 翊.超低频和极低频电磁波的传播及噪声[M].北京:国防工业出版社,2011.

