地震动反应谱拟合过程中小波基函数的选取*

白 泉 韩晶晶, 盛国华 张正帅

1) 中国沈阳110870沈阳工业大学建筑与土木工程学院 2) 中国济南250014山东省地震局



地震动反应谱拟合过程中小波基函数的选取*

1) 中国沈阳110870沈阳工业大学建筑与土木工程学院 2) 中国济南250014山东省地震局

基于目标功率谱， 本文从定量角度提出一种地震动反应谱拟合过程中小波基函数的选取方法． 首先通过修正不同小波基函数所对应的小波系数来拟合地震动反应谱； 然后设定总体误差绝对值和误差均方差这两个定量指标来描述各拟合波功率谱与目标功率谱的差异， 借助数理统计的独立权数原理， 求得不同小波基函数所对应的定量指标的综合评价值； 最后对比综合评价值, 得到拟合精度最高、 误差离散最小的最优小波基． 应用该方法， 选取8种常见的小波基函数进行实例分析． 结果表明， 该方法得到的最优拟合波与原信号差异不大， 拟合波反应谱、 功率谱与目标反应谱、 功率谱均吻合得较好， 从而验证了该方法的正确性．

小波基函数 地震动反应谱拟合 最优基 功率谱 非平稳特性

引言

近年来， 被誉为数学“显微镜”的小波变换已成为分析与处理地震动信号的一种新兴且有效的工具． 常用的小波基函数种类众多， 其本身也具有多样性， 在地震动反应谱拟合过程中， 应用小波变换对同一地震波进行分析时， 由于选用的小波基函数不同， 因而分析结果差异很大．

基于小波变换的地震动反应谱拟合主要是对给定的初始时程进行小波分解得到小波分量， 通过调整小波分量， 使地震动加速度时程反应谱逼近给定的目标谱(Scanlan， Sachs， 1974； Mukherjee， Gupta， 2002； 谢异同等， 2011a， b)， 其中选择小波基函数是较为关键的步骤． Scanlan和Sachs(1974)提出频域调整法， 通过在初始地震动加速度时程上叠加窄带小波来拟合地震动反应谱． Mukherjee和Gupta(2002)借助小波变换提出了一种迭代修正目标反应谱的方法． 谢异同等(2011a)提出一种同时对多阻尼比目标反应谱拟合的方法， 以阿里亚斯强度作为控制参数， 分两次来调整地震动； 同样地， 其选用紧支撑的半正交B样条小波对地震动进行分解(谢异同等， 2011b)， 通过对各分量能量谱峰值的分析， 进而对地震动进行调整． 樊剑等(2009)采用db4小波和谐小波作为母小波， 分别对Northridge波作离散小波变换， 得到了信号功率谱图和小波重构图． 相比之下， 谐小波变换在频域内具有较高的频谱描述能力， 而db4小波在时间域的重构能力较谐小波强． 白泉等(2013)选用具有较好正则性、 衰减快且频域上具有紧支集的Meyer小波作为母小波， 通过静态离散小波变换提出一种地震动加速度时程的调整方法．

在拟合非平稳地震信号时， 现有研究(高静怀等， 1996； Giaralis， Spanos， 2009； 曾宪伟等， 2010； 张郁山， 赵凤新， 2014)大部分只是从定性角度分析选择小波基函数． 本文从定量角度提出一种地震动反应谱拟合过程中小波基函数的选取方法． 该方法基于改进的金井清谱， 依据已存在的小波系数迭代修正法拟合地震动反应谱. 通过选取8种不同的小波基函数对同一地震波, 即Taft波进行小波分解和小波系数修正、 重构， 得到各自所对应的拟合地震动反应谱； 通过分析对比拟合波功率谱与目标功率谱的总体误差绝对值和误差均方差， 并对其进行综合评价， 从而得到地震动反应谱拟合的最优小波基．

1 基于小波变换的地震动反应谱拟合

对于任意信号x(t)， 经过j尺度的小波变换都可以表示为小波序列y(j，k)的线性组合， 即

(1)

式中：V(j，k)为小波系数；ψ(j,k)为依赖于参数j和k的小波基函数，j为尺度因子，k为平移因子；N为信号采样点数.y(j，k)的具体表达式参见彭玉华(1999)著作．

小波系数主要对频率位于某特定尺度所对应频带的单自由度振子的反应有较大贡献(Basu， Gupta， 1997)． 在此基础上， 本文借助小波系数修正法， 先求出不同尺度所对应频带的目标反应谱在该频带上所围的面积， 同样地求出修正之前重构波反应谱在该频带上所围的面积； 然后将二者比值作为修正系数， 对小波系数进行调整． 但是根据动力学原理， 调整某一特定频带的地震动将会对相邻频带地震动产生影响， 从而影响拟合精度． 因此， 需要采用迭代法对各频带的小波系数进行修正． 本文依据现有文献(樊剑等， 2009； 谢异同等， 2011a； 张郁山， 赵凤新， 2014)设定迭代次数10次作为终止条件， 则经迭代修正后的系数表达式为

(2)

2 小波基函数的选取

2.1 小波基函数选取的判别方法

小波基函数即小波分析的基， 不是唯一存在的， 所有满足小波条件的函数都可以作为小波基函数， 故其选取就显得尤为重要． 选取小波基函数常用的方法主要有以下3种(杨福生， 1999； 高志， 余啸海， 2007)：

1) 利用自相似函数． 对于小波变换， 如果选择的小波基函数对信号有一定的相似性， 则变换后的能量比较集中， 可以有效减少计算量， 如下式：

(3)

式中若χ2j(t)与x(t)有某种程度上的相似， 则变换后的能量比较集中， 计算量小．

2) 利用判别函数． 针对本文地震动反应谱拟合问题， 找出一些关键性技术指标， 例如拟合谱与目标谱的总体误差绝对值和误差均方差等， 得到一个判别函数， 将各种小波基函数带入其中， 通过对比得到最优基．

3) 利用支集长度． 大部分应用选择支基长度为5—9的小波， 因为支集太长会产生边界问题， 支集太短则消失矩太低， 不利于信号能量的集中．

本文在地震动反应谱拟合过程中选用判别函数法. 通过选取判别函数， 以拟合波功率谱与给定目标功率谱之间的总体误差绝对值和误差均方差作为定量指标， 进行小波基函数的选取． 以实测的Taft地震波作为母波， 以与《建筑抗震设计规范》(中华人民共和国住房和城乡建设部， 中华人民共和国国家质量监督检验检疫总局， 2010)建议的反应谱相容的功率谱函数----改进的金井清谱(欧进萍， 王光远， 1998)作为目标功率谱， 通过小波变换对各个尺度上的小波系数进行迭代修正， 重构得到拟合地震动反应谱．

上述所用的目标功率谱是基于金井清模型， 经欧进萍和王光远(1998)修正后得到， 其函数表达式为

(4)

式中：ζg和ωg分别为地表土层阻尼比和固有圆频率；ωr为基岩特性的谱参数， 取值为8π；S0为谱强度因子， 是反映地震动强弱的谱参数．

2.2 小波基函数的选取

本文主要从定量方面分析地震波功率谱与目标功率谱的差异， 具体来讲即对比拟合地震波功率谱与目标功率谱的总体误差绝对值和误差均方差的大小， 并对二者进行综合评价， 以得到拟合精度高的小波基函数．

根据功率谱密度函数的定义以及小波基函数之间的正交性， 可得功率谱密度函数与小波系数之间的关系， 即

(5)

式中, Δf为尺度j所对应的频带宽度，G(fj)为功率谱密度函数在fj处的值．

通过判别函数法确定小波基函数， 以功率谱总体误差绝对值和误差均方差作为判别函数的两个指标， 其表达式分别为(樊剑等， 2008)

(6)

(7)

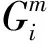
通过对比不同小波基函数得出的μ值和σ值， 选出精度高、 误差小的小波基函数作为拟合波的最优基函数． 但是仅独立地比较这两个指标值， 并不能综合提取最优小波基函数， 而需要对这两个指标进行综合评价． 本文借助数理统计中的多元分析方法----独立权数法， 通过确定这两个指标的权重对其进行综合评价． 在此引入复相关系数R对上述两个指标进行综合评价， 其计算公式为(吴祈宗， 侯福均， 2013)

(8)

以复相关系数R的倒数作为各指标的权重， 求取各小波基函数的综合评价值， 即

(9)

根据上述两个指标的表现意义， 最终取ω最小值时所对应的小波基为最优小波基．

3 实例分析

依据上述地震动反应谱拟合过程以及小波基函数的选取方法， 以Taft波作为母波， 选取8种不同的小波基函数进行地震动反应谱拟合. 通过综合分析各定量指标， 从中选取拟合地震动反应谱的最优小波基． 本文采用薛素铎等(2003)和梁建文(2005)给出的与《建筑抗震设计规范》(中华人民共和国住房和城乡建设部， 中华人民共和国国家质量监督检验检疫总局， 2010)相对应的目标功率谱函数(式(4))中各参数的取值， 选择Ⅷ度地震、 Ⅲ类场地中设计地震分组为第1组的场地条件. 各参数具体取值为ζg=0.8，ωg=4π，S0=232.6 cm2/s3．

由于用于小波分解的小波基函数种类众多， 本文仅以haar， db4， db8， dmey， sym5， coif5， bior3.9和bior6.8等8种小波为例， 按照上述的小波基函数选择方法， 通过MATLAB编程， 对Taft波进行小波分解， 分解层数为7层， 计算得到了μ，σ和ω值， 如表1所示． 可以看出，μ值越小， 说明拟合地震波功率谱与目标功率谱的差异越小， 拟合波精度越高；σ值越小， 说明误差离散越小， 拟合波的整体性越好. 取w最小值时所对应的小波基为最优小波基， 即sym5为本文方法所得到的最优小波基. 选用该小波基函数， 对Taft波进行7层小波分解， 迭代修正10次重构得到拟合波.

表1 不同小波基函数下拟合波的总体误差绝对值μ、 误差均方差σ和综合评价值ω

图1为Taft母波与拟合波的加速度时程对比图． 可以看出， 调整系数后重构的地震动加速度时程与原信号的地震动加速度时程差异不大， 即运用本文所选的小波基函数能够保留原始信号在时域上的非平稳特性． 图2为原信号、 拟合信号与目标信号反应谱对比图． 可以看出， 相比原信号反应谱， 调整后拟合信号反应谱与目标信号反应谱更为符合， 证明最优基的选择保证了重构的精度. 但由于小波变换只能详细分析信号的低频部分， 因此出现一些拟合顽固点， 这一问题将在后期利用小波包变换进行解决． 图3为基于Taft母波的拟合地震波功率谱与改进的金井清目标功率谱对比图． 可以看出， 依据调整后的小波系数重构得到的拟合地震波功率谱与目标功率谱符合较好， 说明要分析信号时频域上的特性， 在进行信号拟合时选择合适的小波基函数非常关键．

4 讨论与结论

在拟合地震动反应谱应用中， 选用不同的小波基函数拟合同一地震动反应谱的精度一般是不同的， 且现有研究多是定性分析不同小波基函数对拟合地震动反应谱的影响， 因此提供一种合理选取高精度小波基函数的方法显得尤为重要． 本文以小波变换为研究工具， 从定量角度提出一种地震动反应谱拟合过程中选择小波基函数的方法. 基于该方法， 以haar, db4, db8, dmey, sym5, coif5, bior3.9和bior6.8等8种小波基函数为例， 通过MATLAB编程进行实例分析. 结果表明： 8种不同小波基函数得到的总体误差绝对值μ各不相同， 误差均方差σ也各不相同；μ值越小， 拟合地震波功率谱与目标功率谱的差异越小；σ值越小， 拟合波的整体性越好； 对于不同的小波基函数拟合同一地震动反应谱时， 拟合波功率谱的合成精度不同； 综合评价值ω从定量方面直接得到拟合波的最优基； 加速度时程反应谱曲线以及功率谱曲线的吻合程度则直观地展现了最优小波基所对应的较高拟合精度．

图1 Taft母波(a)与拟合波(b)的加速度时程对比

图2 原信号、 拟合信号与目标信号反应谱对比

图3 拟合地震波功率谱与目标功率谱对比

需要指出的是， 在对本文所采用的方法进行验证时， 只选取了8种现有且常见的小波基函数， 适用范围并不明确． 例如， 对于构造的小波基函数是否适用， 当同时选用现有小波基和构造小波基时是否适用等， 还有待进一步探讨． 此外， 本文提出的小波基函数选择法是基于实测地震记录Taft波、 地震烈度为Ⅷ度、 场地类别为Ⅲ类， 设计地震分组为第1组的地区， 故有一定的局限性． 如需得到适用于所有地震记录、 所有场地的最优基， 还需进一步研究． 由于小波变换只能详细分析信号的低频部分， 因此文中所述方法的拟合过程会出现一些拟合顽固点， 该问题将在后期利用小波包变换来解决．

白泉， 付亮华， 鲍文博， 金生吉. 2013. 基于静态离散小波变换的地震动时程调整[J]. 沈阳工业大学学报， 35(4): 469--474.

Bai Q， Fu L H， Bao W B， Jin S J. 2013. Ground motion time-history modulation based on stationary discrete wavelet transform[J].JournalofShenyangUniversityofTechnology， 35(4): 469--474 (in Chinese).

樊剑， 刘铁， 魏俊杰. 2008. 基于小波包变换的人工地震波合成[J]. 华中科技大学学报： 自然科学版， 36(3): 42--45.

Fan J， Liu T， Wei J J. 2008. Generation of artificial earthquakesviathe wavelet packet transform[J].JournalofHuazhongUniversityofScienceandTechnology：NaturalScienceEdition， 36(3): 42--45 (in Chinese).

樊剑， 吕超， 张辉. 2009. 基于离散谐小波变换的地震波时变谱估计及非平稳地震波人工合成[J]. 地震学报， 31(3): 333--341.

Fan J， Lü C， Zhang H. 2009. Time-varying spectrum estimation and artificial non-stationary ground motion simulationviadyadic harmonic wavelet transform[J].ActaSeismologicaSinica， 31(3): 333--341 (in Chinese).

高静怀， 汪文秉， 朱光明， 彭玉华， 王玉贵. 1996. 地震资料处理中小波函数的选取研究[J]. 地球物理学报， 39(3): 392--399.

Gao J H， Wang W B， Zhu G M， Peng Y H， Wang Y G. 1996. On the choice of wavelet functions for seismic data processing[J].ActaGeophysicaSinica， 39(3): 392--399 (in Chinese).

高志， 余啸海. 2007. Matlab小波分析与应用[M]. 第2版. 北京: 国防工业出版社: 9--61.

Gao Z， Yu X H. 2007.MatlabAnalysisandApplicationofWavelet[M]. 2nd ed. Beijing: National Defense Industry Press: 9--61 (in Chinese).

梁建文. 2005. 非平稳地震动过程模拟方法(I)[J]. 地震学报， 27(2): 213--224.

Liang J W. 2005. Simulation of non-stationary ground motion processes (I)[J].ActaSeismologicaSinica， 27(2): 213--224 (in Chinese).

欧进萍， 王光远. 1998. 结构随机振动[M]. 北京: 高等教育出版社: 109--175.

Ou J P， Wang G Y. 1998.RandomVibrationofStructures[M]. Beijing: Higher Education Press: 109--175 (in Chinese).

彭玉华. 1999. 小波变换与工程应用[M]. 北京: 科学出版社: 21--69.

Peng Y H. 1999.WaveletTransformandEngineeringApplication[M]. Beijing: Science Press: 21--69 (in Chinese).

吴祈宗， 侯福均. 2013. 运筹学与最优化方法[M]. 第2版. 北京: 机械工业出版社: 45--156.

Wu Q Z， Hou F J. 2013.OperationsResearchandOptimizationMethods[M]. 2nd ed. Beijing: China Machine Press: 45--156 (in Chinese).

谢异同， 盛涛， 袁俊. 2011a. 拟合多阻尼比目标反应谱的高精度地震动调整方法[J]. 西北地震学报， 33(3): 223--227.

Xie Y T， Sheng T， Yuan J. 2011a. A modification method of earthquake ground motion with high precision from fitting the multi-damping-ratio target spectrum[J].NorthwesternSeismologicalJournal， 33(3): 223--227 (in Chinese).

谢异同， 葛兴云， 曲高峰， 邵辉成. 2011b. 基于小波分解的能量谱分析方法及其在汶川地震中的应用[J]. 世界地震工程， 27(3): 66--72.

Xie Y T， Ge X Y， Qu G F， Shao H C. 2011b. Wavelet-based analysis of the energy spectrum and its application to Wenchuan earthquake[J].WorldEarthquakeEngineering， 27(3): 66--72 (in Chinese).

薛素铎， 王雪生， 曹资. 2003. 基于新抗震规范的地震动随机模型参数研究[J]. 土木工程学报， 36(5): 5--10.

Xue S D， Wang X S， Cao Z. 2003. Parameters study on seismic random model based on the new seismic code[J].ChinaCivilEngineeringJournal， 36(5): 5--10 (in Chinese).

杨福生. 1999. 小波变换的工程分析与应用[M]. 北京: 科学出版社: 35--78.

Yang F S. 1999.WaveletTransformforProjectAnalysisandApplication[M]. Beijing: Science Press: 35--78 (in Chinese).

曾宪伟， 赵卫明， 师海阔， 李自芮. 2010. 利用小波包变换对地震信号进行时频分析时小波基函数的选取[J]. 地震研究， 33(4): 323--328.

Zeng X W， Zhao W M， Shi H K， Li Z R. 2010. Selection of wavelet basis function in process of time-frequency analysis of earthquake signals using wavelet packet transform[J].JournalofSeismologicalResearch， 33(4): 323--328 (in Chinese).

张郁山， 赵凤新. 2014. 基于小波函数的地震动反应谱拟合方法[J]. 土木工程学报， 47(1): 70--81.

Zhang Y S， Zhao F X. 2014. Matching method of ground-motion response spectrum based on the wavelet function[J].ChinaCivilEngineeringJournal， 47(1): 70--81 (in Chinese).

中华人民共和国住房和城乡建设部， 中华人民共和国国家质量监督检验检疫总局. 2010. 建筑抗震设计规范(GB 50011—2010)[S]. 北京: 中国建筑工业出版社： 6--17， 31--47.

Ministry of Housing and Urban-Rural Development of the People’s Republic of China， General Administration of Quality Supervision， Inspection and Quarantine of the People’s Republic of China. 2010.CodeforSeismicDesignofBuildings(GB50011--2010)[S]. Beijing: China Architecture & Building Press： 6--17， 31--47 (in Chinese).

Basu B， Gupta V K. 1997. Non-stationary seismic response of MDOF systems by wavelet transform[J].EarthqEngStructDyn， 26(2): 1243--1258.

Giaralis A， Spanos P D． 2009. Wavelet-based response spectrum compatible synthesis of accelerograms: Eurocode application (EC8)[J]．SoilDynEarthqEng， 29(1): 219--235.

Mukherjee S， Gupta V K. 2002. Wavelet-based generation of spectrum-compatible time-histories[J].SoilDynEarthqEng， 22(9/10/11/12): 799--804.

Scanlan R H， Sachs K. 1974. Earthquake time histories and response spectra[J].JEngMechDiv， 100(4): 635--655.

Selection of wavelet basis function in the simulation of seismic response spectrum

1)SchoolofArchitectureandCivilEngineering，ShenyangUniversityofTechnology，Shenyang110870，China2)EarthquakeAdministrationofShandongProvince，Ji’nan250014，China

Based on the target power spectrum， this paper proposed a method for selecting wavelet basis function in the simulation of seismic response spectrum from a quantitative point of view. Firstly， we revised the different wavelet coefficients that correspond to different wavelet basis functions to simulate the seismic response spectrum. And then we set two quantitative indices,i.e.， overall error absolute values and mean square errors to describe the differences between the power spectrum of the simulated wave and the target power spectrum. Using the principle of independent weight in mathematical statistics， we obtained the comprehensive evaluation values of the quantitative indices that correspond to the different wavelet basis functions. Finally， from all of the comprehensive evaluation values， we got the optimal wavelet basis with highest simulation accuracy and minimum discreteness of error. Using this method， we selected eight kinds of common wavelet basis functions for instance analysis. The results show that the optimal simulated wave based on this method has slight difference from the original signal， and simulated wave response spectrum coincides well with the target response spectrum， the same as power spectrum, verifying the correctness of the method proposed in this paper.

wavelet basis function； simulation of seismic response spectrum； optimum basis； power spectrum； non-stationary characteristic

10.11939/jass.2015.06.013.

辽宁省教育厅基金项目(L2013050)资助.

2015-05-15收到初稿， 2015-08-17决定采用修改稿.

e-mail: hanjingjing_stu@163.com

10.11939/jass.2015.06.013

P315.3+1

A

白泉， 韩晶晶, 盛国华， 张正帅. 2015. 地震动反应谱拟合过程中小波基函数的选取. 地震学报, 37(6): 1037--1044.

Bai Q, Han J J, Sheng G H, Zhang Z S. 2015. Selection of wavelet basis function in the simulation of seismic response spectrum .ActaSeismologicaSinica, 37(6): 1037--1044. doi:10.11939/jass.2015.06.013.