基于特征地震模型含时间的概率地震危险性分析方法及其应用研究*

李昌珑 徐伟进 吴 健 高孟潭

(中国北京100081中国地震局地球物理研究所)



基于特征地震模型含时间的概率地震危险性分析方法及其应用研究*

(中国北京100081中国地震局地球物理研究所)

本文介绍了特征地震的对数正态分布模型、 正态分布模型和布朗过程时间模型， 提出了使用地震破裂面源模型的特征地震含时间的概率地震危险性分析理论和方法. 通过具体算例对不同的特征地震模型进行了比较， 并对特征地震危险性分析方法进行了系统探索. 研究结果表明， 特征地震含时间模型在复发周期早期的地震危险性低于不含时间模型， 而在后期其地震危险性则高于不含时间模型. 特征地震复发周期的对数正态分布模型与布朗过程时间模型计算得出的地震危险性差别不大. 在未到期望复发时间时， 正态分布模型与前两种模型计算的地震危险性差别不大； 而接近期望复发时间及之后时段， 正态分布模型计算的地震危险性则迅速增大.

含时间的概率地震危险性 特征地震 对数正态分布 布朗过程时间模型 地震破裂面源模型

引言

概率地震危险性分析方法(Cornell， 1968)是国内外地震危险性分析普遍使用的方法(胡聿贤， 1999). 地震活动性模型是概率地震危险性分析工作的重要组成部分. 按照地震发生概率是否随时间变化， 地震活动性模型分为两类， 即不含时间模型和含时间模型. 不含时间模型假设地震的发生服从泊松分布， 各震级地震的发生概率均遵从古登堡-里克特的震级-频度关系(G-R关系)(Gutenberg， Richter， 1956)， 也称为泊松模型. 但是根据记录， 许多断层的地震活动性随时间均有较明显的变化， 如果使用泊松模型， 可能会高估或低估一个时间段内的地震危险性， 故对此类断层有必要使用含时间模型.

美国地质调查局在1988年即采用含时间模型对美国加州圣安德烈斯断裂的地震危险性进行了研究(Working Group on California Earthquake Probabilities， 1988). 此后这一研究作为美国地质调查局的日常工作， 每隔几年就会发布关于加州地区的含时间的概率地震危险性研究报告(Working Group on California Earthquake Probabilities， 1988， 1990， 1996， 1999， 2003， 2008; Fieldetal， 2014). 此外， Boyd等(2008)及Hebden和Stein(2009)对美国阿拉斯加地区和新马德里地震区的含时间的概率地震危险性也进行了研究. 国内研究人员对含时间的概率地震危险性也作了初步探讨(闻学泽, 1998； 杨明， 刘百篪， 2000). 将这些研究结果作为不含时间的概率地震危险性分析结果的补充， 为地震设防及地震预测提供服务.

与泊松模型相比， 含时间的概率地震危险性分析模型考虑地震发生的时间序列具有非平稳性. 20世纪70年代以来， 研究人员提出了多种含时间模型， 概括起来主要分为4类： ① 认为地震活动存在平静期和活跃期的分段泊松模型(Shahetal， 1982)； ② 描述地震活动在时间序列上疏密相间的随机点过程模型(Lomnitz-Adler， Lomnitz， 1979)； ③ 基于地震活动时空转移的马尔可夫过程模型(Nishioka， Shah， 1980)； ④ 描述大地震按一定复发周期发生的特征地震模型. 由于各自的局限性， 前3种模型均未得到广泛应用(高孟潭， 1986). 1984年之后， 特征地震模型得到迅速发展， 已经成为当前含时间的概率地震危险性分析中使用较多的模型.

与传统的地震危险性分析相比， 特征地震的地震危险性分析需要考虑两方面问题: ① 特征地震的年发生率与其复发周期相关， 如何选取特征地震的活动性模型是需要研究的问题; ② 特征地震危险性分析考虑的是大地震， 需要使用能够反映大地震震源尺度和几何特征的震源模型计算其对地震动的影响. 对于第一个问题， 目前一些研究仍处于探索阶段. 研究人员考虑不同的特征地震复发间隔模型来描述特征地震的活动性， 如对数正态分布模型(Nishenko， Buland， 1987; 闻学泽， 1998; 杨明， 刘百篪， 2000; Petersenetal， 2007; Hebden， Stein, 2009)、 正态分布模型(Hebden， Stein， 2009)和具有明确物理力学意义的布朗过程时间(Brownian passage-time， 简写为BPT)模型(Matthewsetal， 2002; 冉洪流， 周本刚， 2004). 冉洪流和周本刚(2004)对几种模型在远超复发周期时段的危险性进行比较， 并应用于北京西北地区的研究中. 但是， 对于在任意离逝时间的时段， 各模型特点及适用范围仍是值得研究的问题.

本文在介绍几种特征地震模型的基础上， 使用两个具体实例比较了不同模型的地震危险性计算结果， 并对上面第一个问题进行了探索. 对于第二个问题， 本文考虑将潜在破裂面源模型应用于特征地震危险性计算中. 另外， 本文在已有的场点地震动参数年超越概率计算公式的基础上， 对特征地震的危险性计算公式进行了推导， 提出了特征地震的场点地震动参数年超越概率的计算公式. 通过地震危险性的计算实例， 给出了基于特征地震的地震危险性分析方法， 并总结了一套计算特征地震危险性的完整步骤.

1 特征地震活动性模型

1.1 特征地震概念和性质

特征地震的概念最早由Schwartz和Coppersmith(1984)提出， 用于解释圣安德烈斯断层和瓦塞赤断层周期性发生M≥6.0地震， 而M5.0左右地震缺失的现象. 根据当前对特征地震已有的研究成果(Wesnousky， 1994; 闻学泽， 1995; 杨明， 刘百篪， 2000; 薛霆虓等， 2010)表明， 含时间的概率地震危险性分析主要考虑特征地震的以下性质： ① 特征地震的复发间隔具有准周期性， 其在原地复发具有相似的震源特征， 对某一特征地震活动区， 一般可获得历史上多次特征地震活动的序列； ② 特征地震震级一般为所在地震活动区的最大震级； ③ 震级在不超过特征地震最大余震震级的地震服从泊松分布， 震级在特征地震震级与其最大余震震级之间的地震缺失．

还须指出的是， 本文的特征地震模型及相应的地震危险性分析仅考虑特征地震， 并根据上述性质③假设特征地震震级与最大余震震级之间的震级档的地震发生率为0. 实际应用时， 不超过最大余震震级的震级档对地震危险性的贡献按照不含时间模型进行分析， 本文不作讨论.

1.2 特征地震震级模型

对于特征地震的震级模型， 董瑞树等(2000)曾提出将混合地震模型用于中国西部的活动断裂， 即建立一个特征地震的起算震级， 起算震级以下的地震服从泊松分布， 以上地震均为特征地震. 但是， 根据上节所述性质， 由于经常存在小于特征地震震级的某些震级段地震缺失的现象， 故仅假设一个起算震级不能完全反映此类地区的地震活动性. 另外考虑到震级的不确定性， 杨明和刘百篪(2000)认为特征地震震级存在一个范围， 其上限为所在震源区的地震震级上限Mμ， 下限为Mμ-0.5. 因此本文使用的特征地震震级MC的分布范围为[Mμ-0.5，Mμ] ， 将特征地震最大余震的震级作为服从泊松分布的地震震级上限.

1.3 特征地震复发间隔模型

前文已经提到， 特征地震的复发具有准周期性， 但地震发生时间存在自身的不确定性， 不可能按照某个时间间隔精确地发生. 由于特征地震震级比较固定， 因此特征地震复发间隔模型的建立成为特征地震危险性分析的关键环节. 目前使用较多的特征地震复发间隔模型主要有对数正态分布模型、 正态分布模型和BPT模型. 以下分别介绍这3种模型.

1.3.1 对数正态分布模型

对数正态分布模型源于Nishenko和Buland(1987)对环太平洋地震带地区的复发大地震的研究. 该研究认为， 整个环太平洋地区的特征地震复发间隔均服从归一化的对数正态分布， 其概率密度函数为

(1)

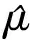
Petersen等(2007)对对数正态分布模型进行了研究， 提出了直接使用某一地区特征地震序列的对数正态分布模型． 该模型设该地区(n+1)次特征地震的复发间隔分别为T1，T2， …，Tn， 则复发时刻t的概率密度函数为

(2)

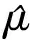
(3)

1.3.2 正态分布模型

正态分布模型也是一种使用较多的特征地震复发间隔模型(Hebden， Stein， 2009). 设(n+1)次特征地震的复发间隔分别为T1，T2， …，Tn， 则正态分布模型中复发时刻t的概率密度函数可表示为

(4)

式中，μ为复发间隔的均值，σ为标准差， 分别满足

(5)

(6)

1.3.3 布朗过程时间(BPT)模型

Matthews等(2002)对Reid(1911)的弹性回跳理论作了改进， 提出了地震复发的BPT模型. 该模型假设发震断层的应力以恒定的速率积累， 而特征地震的复发间隔服从正态分布， 均值和标准差分别为应力积累和扩散速率的函数(朱元清等， 2013). 在实际应用中， 均值和标准差可直接由特征地震序列计算得到. 该模型在理论上反映了地震孕育和发生的内在物理机制， 是近年来使用较多的模型. 该模型的概率密度函数可表示为

(7)

式中，μ为复发间隔的均值，σ为复发间隔的标准差，α=σ/μ.

1.4 特征地震发生率

已知特征地震复发间隔的分布， 即可计算在未来时间段(te,te+Δt)内的特征地震发生率P(杨明， 刘百篪， 2000)：

(8)

式中，P为特征地震在(te,te+Δt)时间段内发生， 且在(0,te)内不发生的概率.

为了进行地震危险性计算， 还需要知道特征地震在(te,te+Δt)时间段内的年发生率r. 由式(8)已知特征地震在Δt时段内的发生率P， 则r仍服从泊松分布(Petersenetal， 2007)：

(9)

2 基于特征地震模型含时间的概率地震危险性计算

前面介绍了含时间的地震活动性模型， 再结合潜在震源模型和地震动衰减关系模型， 可计算含时间的概率地震危险性. 本文仅假设潜在震源区的地震活动性随时间变化， 而震源模型和地震动衰减关系模型在考虑时段内则恒定不变， 与不含时间的概率地震危险性分析所使用的模型相同. 下面介绍含时间的概率地震危险性分析时所使用的震源模型和地震动衰减关系模型， 以及地震危险性的计算方法.

2.1 特征地震震源模型和地震动衰减关系模型

由于特征地震的震级通常较大， 造成大面积的断层破裂， 因此本文的特征地震危险性分析模型使用胥广银和高孟潭(2007)提出的地震破裂面源模型. 该模型将场点到地震破裂面的最短距离作为距离参数， 相应的衰减关系选用地震破裂面距的衰减关系.

为了确定地震破裂面的大小， 还需计算出破裂面的长度和宽度. 破裂面长度和宽度根据Wells和Coppersmith(1994)提出的震级与破裂面长度、 宽度关系式分别进行计算， 即

lgL=-1.43+0.88MW,

(10)

(11)

式中，L为破裂面长度，W为破裂面宽度，MW为矩震级.

2.2 特征地震模型的概率地震危险性计算

设对场点产生影响的潜在破裂面源区有N个， 第k个潜在破裂面源区的面积为Sk,mj为第j个震级档的中心值， 震级为mj的地震发生在第k个潜在破裂面源区内的概率为fk， mj， 则有

(12)

式中，P[(x,y)k|mj]为第k个潜在破裂面源区内发生一次震级为mj、 位置为(x，y)的地震的概率.

根据潘华等(2013)提出的场点地震危险性计算公式， 可推出在第k个潜在破裂面源区内随机发生一次震级为mj、 位置为(x，y)的地震， 在场点造成的地震动参数A达到或超过给定地震动参数a的概率为

(13)

式中，Nm为震级分档数，P[A≥a|mj, (x,y)k]与所预测地震动的衰减关系不确定性相关，P(mj)k为第k个潜在破裂面源区震级的概率分布， 震级-频度关系符合G-R关系.P(mj)的表达式为

(14)

式中：β=bln10，b为地震统计区的b值；m0为地震统计区震级下限；mu为震级上限.

对于本文特征地震模型， 取式(14)中的Δm为0.5. 由1.2节可知， 特征地震只有一个震级档， 设Mc为特征地震震级档的中心值， 则式(13)中Nm=1， 式(14)中mj=Mc，m0=Mc-0.25，mu=Mc+0.25， Δm=0.5， 故式(14)可简化为

(15)

P(mj)为某个潜在破裂面源区的震级的概率分布， 则第k个潜在破裂面源区的震级概率分布P(mj)k为

(16)

则式(13)可简化为

(17)

令P(A≥a)k=pk， 可得第k个潜在破裂面源区内发生的地震在场点产生A≥a的地震动年超越概率为

(18)

式中，rk为第k个潜在破裂面源区内特征地震的年发生率， 可由式(9)计算得出.

综合场点周围N个潜在破裂面源区对场点的影响， 由全概率定律可得

(19)

综合式(12)—(19)， 可得场点产生A≥a的地震动年超越概率为

(20)

3 使用不同模型的地震危险性分析实例

前面介绍了对数正态分布模型、 正态分布模型和BPT模型等3种地震活动性模型， 几种模型计算地震危险性的效果如何， 各自适用于多长的离逝时间， 还需进一步研究. 本节选取郯庐断裂带莒县—郯城段和山西交城断裂进行地震危险性实例分析， 并比较不同模型的计算结果.

3.1 郯庐断裂带莒县—郯城段的地震危险性分析

3.1.1 特征地震危险性模型的建立

分别使用不含时间模型、 对数正态分布模型、 正态分布模型和BPT模型计算郯庐断裂带莒县—郯城段及其周边地区的地震危险性， 并对正态分布模型与对数正态分布模型结果进行比较.

图1 对数正态分布模型、 正态分布模型和BPT模型的概率密度

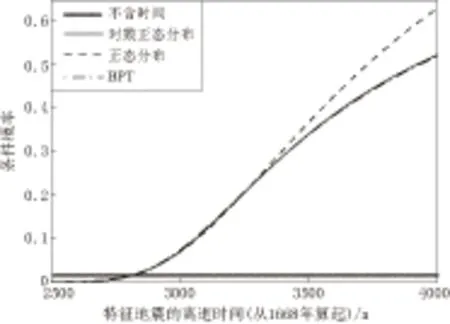
图2 不含时间模型和3种含时间模型的50年内地震发生的条件概率

计算时段地震年发生率对数正态分布模型正态分布模型BPT模型公元4550—4600年0．01970．03220．0197公元4850—4900年0．02170．04970．0218公元5000—5050年0．02250．06080．0227

对于对数正态分布模型、 正态分布模型和BPT模型， 下次特征地震发生时间的期望值约为t=3227 a. 由图2和表1可以看出， 在期望复发时间段早期， 特征地震发生概率极小. 在t=2800 a 前， 含时间模型的地震发生概率小于不含时间模型； 在t=3000 a附近， 含时间模型的地震发生概率明显大于不含时间模型; 超过t=3227 a后， 如果特征地震仍未发生， 则含时间模型的地震发生概率继续增大， 其中正态分布模型的增大较快.

3.1.2 不含时间模型和3种含时间模型的地震危险性计算

根据前面建立的特征地震模型， 利用式(20)计算断层周边场点的水平基岩峰值加速度超越概率. 衰减关系选自Sadigh等(1997)提出的衰减关系：

(21)

式中，y为水平基岩峰值加速度，MW为矩震级，Rrup为场点到地震破裂面的最短距离．各项系数如表2所示．

表2 地震动衰减关系系数(引自Sadigh et al， 1997)

图3分别给出了不含时间模型和3种含时间模型在公元4550—4600年、 公元4850—4900年和公元5000—5050年时段内郯庐断裂带莒县—郯城段及其附近地区50年超越概率2%峰值加速度的地震危险性. 可以看出， 郯庐断裂带莒县—郯城段在公元4550—4600年含时间模型的地震危险性小于不含时间模型； 在公元4850—4900年和公元5000—5050年的地震危险性大于不含时间模型. 在超过期望复发时间的公元5000—5050年， 地震危险性较包含期望复发时间的公元4850—4900年更大. 对数正态分布模型与BPT模型计算的地震危险性始终差别不大； 在超过期望复发时间后， 正态分布模型计算的地震危险性较另两种含时间模型显著增大.

3.2 山西交城断裂的地震危险性分析

上节以郯庐断裂带为例， 阐述了含时间的概率地震危险性分析的计算过程. 由于郯庐断裂带的大地震离逝时间较短， 使得用含时间模型计算的当前地震危险性较小， 现实意义不大. 因此， 本节选取了大地震离逝时间较长的山西交城断裂， 计算不同模型的地震危险性并作了比较. 交城断裂位于山西太原西南方， 大致呈NE--SW走向．

根据郭慧等(2012)研究资料， 交城断裂的3次古地震事件发生时间距今分别为3060—3530年、 5320—6140年和8360年左右； 3次古地震事件的时间间隔分别为2020—2840年和2220—3040年. 古地震震级M≥7. 本文选取特征地震的震级档为M7.0—7.5， 地震离逝时间为3000年， 3次古地震事件的时间间隔分别取2430年和2630年. 计算过程与上节类似， 计算出交城断裂公元2015—2065年的特征地震年发生率， 如表3所示.

表3 对数正态分布模型、 正态分布模型和BPT模型在公元2015—2065年的地震年发生率

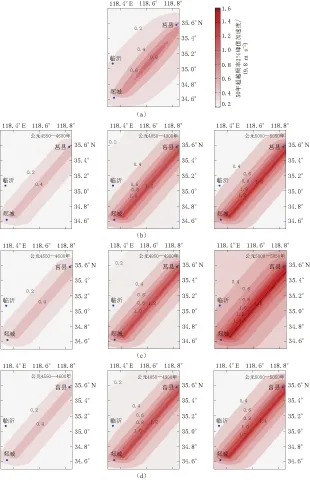
图3 不同模型计算的郯庐断裂带莒县—郯城段及其附近地区的50年超越概率2%峰值加速度的地震危险性

为便于比较， 与上节类似， 仅考虑特征地震震级档的地震危险性， 背景地震的地震危险性不予以计算. 图4给出了山西交城断裂及其附近地区的50年超越概率10%峰值加速度的地震危险性. 可以看出： 在未来50年， 使用含时间模型计算的交城断裂及其附近地区的地震危险性远大于不含时间模型； 对数正态分布模型与BPT模型计算的地震危险性差别不大， 略小于正态分布模型.

图4 不同模型计算的交城断裂及其附近地区2015—2065年的50年超越概率10%峰值加速度的地震危险性

3.3 不同模型计算的地震危险性比较

通过对郯庐断裂带莒县—郯城段与交城断裂的地震危险性比较， 得出以下结果：

1) 计算时段的地震危险性随接近复发周期而增加， 当计算时段超过复发周期后， 如果特征地震仍未发生， 则地震危险性继续增加；

2) 处在复发周期早期阶段的地震危险性低于不含时间模型， 接近及超过复发周期时段的地震危险性明显大于不含时间模型；

3) 3种特征地震模型的危险性计算结果在尚未接近复发周期时差别不大， 接近复发周期及之后， 正态分布模型计算的地震危险性迅速增大， 对数正态分布模型与BPT模型计算的地震危险性始终差别不大.

4 讨论与结论

本文介绍了特征地震模型以及基于特征地震模型含时间的概率地震危险性计算， 并对不同模型的特征地震危险性计算方法进行了比较， 得出以下结论：

1) 根据地震活动性(历史地震、 古地震等)或地球动力学资料建立特征地震的概率密度函数是基于特征地震发生含时间的概率地震危险性分析的关键步骤. 对场点含时间的概率地震危险性分析可按如下步骤进行： ① 对影响场点的潜在震源区进行地质调查和历史地震资料收集， 得到各次大地震的震级和复发间隔， 判断大地震是否符合特征地震性质， 对于已有相关研究的地区， 可直接应用相关资料； ② 对每次特征地震的发震构造(潜在震源区)根据实际情况选择复发间隔的概率密度计算式； ③ 选定计算时段， 计算特征地震年发生率； ④ 结合适当的震源模型(如破裂面源模型)和地震动衰减关系模型， 计算场点的地震危险性.

2) 特征地震模型在期望复发时间段早期的地震危险性低于不含时间模型， 而接近期望复发时间及之后的地震危险性大于不含时间模型. 该结果在一定程度上解决了不含时间模型可能高估或低估大地震危险性的问题.

3) 对数正态分布模型、 正态分布模型和BPT模型计算的地震危险性在未到期望复发时间段时差别不大； 接近期望复发时间及之后， 三者差别较大; 超过期望复发时间后， 正态分布模型计算的地震危险性迅速增大， 而对数正态分布模型与BPT模型则始终差别不大.

4) 郯庐断裂带莒县—郯城段未来数百年发生特征地震的危险性较低， 而山西交城断裂未来50年发生特征地震的危险性较高.

对上述结论， 作以下几点讨论：

1) 本文使用的地震破裂面源参数的选取依据Wells和Coppersmith(1994)提出的模型， 但是实际地震发生具有复杂性， 不同地区和动力学环境下地震破裂尺度可能与模型假设的破裂尺度存在偏差， 应根据地震学、 地质学等多种手段进行特定断裂深部精细结构探测， 合理确定震源模型参数， 这是今后需要考虑的问题.

2) 对于如何界定一个时段是否处在期望复发时间段， 目前还没有一个定量标准. 在本文算例中， 大约在距离期望复发时间均值超过两倍标准差的时段， 特征地震的危险性可忽略不计. 这一结论是否具有普遍性， 还有待进一步研究.

3) 由于正态分布模型计算量较小， 故在计算复发周期之内时段的地震危险性时， 如果没有其它特殊要求， 应使用正态分布模型.

4) 无论是对数正态分布模型、 正态分布模型还是BPT模型， 都是对地震活动性的一种假设. 其中BPT模型来自理论推导(Matthewsetal， 2002)， 对数正态分布模型来自观测记录和地质调查的规律总结(Nishenko， Buland， 1987). 这两种模型均具有一定的理论基础， 比正态分布模型更能真实地反映地震活动情况. 而这两种模型计算的地震危险性差别不大， 又相互印证了各自的可靠性. 冉洪流和周本刚(2004)研究指出， 在离逝时间超过复发周期3.5倍的时段， BPT模型优于对数正态分布模型. 但是， 对于如此长的离逝时间， 特征地震假设是否依然成立， 仍需进一步研究. 因此， 对于超过期望复发时间的时段， 对数正态分布模型与BPT模型差别不大， 二者均可使用.

5) 本文将各特征地震震源区考虑为互不相关的震源区， 一处潜在震源区的地震活动不会影响其它震源区的地震活动性. 但已有研究开始考虑断层间相互作用和应力转移问题(Working Group on California Earthquake Probabilities， 2003). 因此， 一处潜在震源区发生的特征地震是否会对临近震源区的地震活动性造成影响， 还需作更多研究.

晁洪太, 李家灵, 崔昭文, 赵清玉. 1994. 郯庐断裂带中段全新世活断层的特征滑动行为与特征地震[J]. 内陆地震, 8(4): 297--304.

Chao H T， Li J L， Cui Z W， Zhao Q Y. 1994. Characteristic slip behavior of the Holocene fault in the central section of the Tanlu fault zone and the characteristic earthquakes[J].InlandEarthquake， 8(4): 297--304 (in Chinese).

董瑞树， 冉洪流， 任国强. 2000. 混合地震模型的建立及其科学意义[J]. 西北地震学报， 22(4): 390--396.

Dong R S， Ran H L， Ren G Q. 2000. Establishment of the mixed seismic model and its scientific significance[J].NorthwesternSeismologicalJournal， 22(4): 390--396 (in Chinese).

高孟潭. 1986. 地震危险性分析方法概述[J]. 国际地震动态， (11): 10--13.

Gao M T. 1986. An outline of the analytic methods for seismic risk assessment[J].RecentDevelopmentinWorldSeismology， (11): 10--13 (in Chinese).

郭慧， 江娃利， 谢新生. 2012. 山西交城断裂北端及中段3个大型探槽全新世断错现象分析[J]. 地震地质， 34(1): 76--92.

Guo H， Jiang W L， Xie X S. 2012. Analysis of Holocene faulting phenomena revealed in the three trenches along the northern and central Jiaocheng fault， Shanxi[J].SeismologyandGeology， 34(1): 76--92 (in Chinese).

胡聿贤. 1999. 地震安全性评价技术教程[M]. 北京: 地震出版社: 215--222.

Hu Y X. 1999.SeismicSafetyEvaluationTechnologyTutorials[M]. Beijing: Seismological Press: 215--222 (in Chinese).

李家灵， 晁洪太， 崔昭文， 赵清玉. 1994. 郯庐活断层的分段及其大震危险性分析[J]. 地震地质， 16(2): 121--126.

Li J L， Chao H T， Cui Z W， Zhao Q Y. 1994. Segmentation of active fault along the Tancheng-Lujiang fault zone and evaluation of strong earthquake risk[J].SeismologyandGeology， 16(2): 121--126 (in Chinese).

潘华， 高孟潭， 谢富仁. 2013. 新版地震区划图地震活动性模型与参数确定[J]. 震灾防御技术， 8(1): 11--23.

Pan H， Gao M T， Xie F R. 2013. The earthquake activity model and seismicity parameters in the new seismic hazard map of China[J].TechnologyforEarthquakeDisasterPrevention， 8(1): 11--23 (in Chinese).

冉洪流， 周本刚. 2004. 布朗模型在北京西北地区的应用[J]. 地震学报， 26(增刊): 96--102.

Ran H L， Zhou B G. 2004. Application of Brownian model in the northwestern Beijing， China[J].ActaSeismologicaSinica， 26(Suppl): 96--102 (in Chinese).

Shah H C， 鲍霭斌， 董伟民. 1982. 地震危险性分析中贝叶斯模型的意义及其应用[J]. 地震工程与工程振动， 2(4): 1--16.

Shah H C， Bao A B， Dong W M. 1982. Implications and application of Bayesian model for seismic hazard analysis[J].EarthquakeEngineeringandEngineeringVibration， 2(4): 1--16 (in Chinese).

闻学泽. 1995. 活动断裂地震潜势的定量评估[M]. 北京: 地震出版社: 1--150.

Wen X Z. 1995.QuantitativeEstimatesofPotentialEarthquakesonActiveFaults[M]. Beijing: Seismological Press: 1--150 (in Chinese).

闻学泽. 1998. 时间相依的活动断裂分段地震危险性评估及其问题[J]. 科学通报， 43(14): 1457--1466.

Wen X Z. 1998. Assessment of time-dependent seismic hazards on segments of active fault， and its problems[J].ChineseScienceBulletin， 43(23): 1937--1950.

胥广银， 高孟潭. 2007. 潜在地震破裂面源模型及在概率地震危险性分析中的应用方法[J]. 地震学报， 29(3): 285--294.

Xu G Y， Gao M T. 2007. Potential rupture surface model and its application on probabilistic seismic hazard analysis[J].ActaSeismologicaSinica， 29(3): 285--294 (in Chinese).

薛霆虓， 邵志刚， 傅容珊. 2010. 特征地震现象和机制分析[J]. 地球物理学进展， 25(6): 1887--1896.

Xue T X， Shao Z G， Fu R S. 2010. The characteristic earthquake and analysis of its mechanism[J].ProgressinGeophysics， 25(6): 1887--1896 (in Chinese).

杨明， 刘百篪. 2000. 时间相依的地震危险性概率分析[J]. 西北地震学报， 22(1): 10--15.

Yang M， Liu B C. 2000. Probabilistic seismic hazard analysis depending on time[J].NorthwesternSeismologicalJournal， 22(1): 10--15 (in Chinese).

朱元清， 解朝娣， 宋秀青. 2013. 断层的大地震复发概率研究[J]. 地震， 33(4): 1--10.

Zhu Y Q， Xie C D， Song X Q. 2013. A study of the recurrence probability of strong earthquake on faults in mainland China[J].Earthquake， 33(4): 1--10 (in Chinese).

Boyd O S， Zeng Y， Bufe C G. 2008. Toward a time-dependent probabilistic seismic hazard analysis for Alaska[G]∥ActiveTectonicsandSeismicPotentialofAlaska，GeophysicalMonograph，Vol. 179. Washington D C: AGU: 399--416.

Cornell C A. 1968. Engineering seismic risk analysis[J].BullSeismolSocAm， 58(5): 1583--1606.

Field E H， Arrowsmith R J， Biasi G P， Bird P， Dawson T E， Felzer K R， Jackson D D， Johnson K M， Jordan T H， Madden C， Michael A J， Milner K R， Page M T， Parsons T， Powers P M， Shaw B E， Thatcher W R， Weldon R J， Zeng Y H. 2014. Uniform California earthquake rupture forecast， version 3 (UCERF3): The time-independent model[J].BullSeismolSocAm， 104(3): 1122--1180.

Gutenberg B， Richter C F. 1956. Magnitude and energy of earthquakes[J].AnnGeophys， 9(1): 1--15.

Hebden J S， Stein S. 2009. Time-dependent seismic hazard maps for the New Madrid seismic zone and Charleston， South Carolina， areas[J].SeismolResLett， 80(1): 12--20.

Lomnitz-Adler J， Lomnitz C. 1979. A modified form of the Gutenberg-Richter magnitude-frequency relation[J].BullSeismolSocAm， 69(4): 1209--1214.

Matthews M V， Ellsworth W L Reasenberg P A. 2002. A Brownian model for recurrent earthquakes[J].BullSeismolSocAm， 92(6): 2233--2250.

Nishenko S P， Buland R. 1987. A generic recurrence interval distribution for earthquake forecasting[J].BullSeismolSocAm， 77(4): 1382--1399.

Nishioka T， Shah H C. 1980. Application of the Markov chain on probability of earthquake occurrence[J].ProcJSCE， (298): 137--145.

Petersen M D， Cao T Q， Campbell K W， Frankel A D. 2007. Time-independent and time-dependent seismic hazard assessment for the State of California: Uniform California earthquake rupture forecast model 1.0[J].SeismolResLett， 78(1): 99--109.

Reid H F. 1911.TheElastic-ReboundTheoryofEarthquakes[M]. California: University of California Press: 1--444.

Sadigh K， Chang C Y， Egan J A， Makdisi F， Youngs R R. 1997. Attenuation relationships for shallow crustal earthquakes based on California strong motion data[J].SeismolResLett， 68(1): 180--189.

Schwartz D P， Coppersmith K J. 1984. Fault behavior and characteristic earthquakes: Examples from the Wasatch and San Andreas fault zones[J].JGeophysRes， 89(B7): 5681--5698.

Wells D L， Coppersmith K J. 1994. New empirical relationships among magnitude， rupture length， rupture width， rupture area， and surface displacement[J].BullSeismolSocAm， 84(4): 974--1002.

Wesnousky S G. 1994. The Gutenberg-Richter or characteristic earthquake distribution， which is it?[J].BullSeismolSocAm， 84(6): 1940--1959.

Working Group on California Earthquake Probabilities. 1988.ProbabilitiesofLargeEarthquakesOccurringinCaliforniaontheSanAndreasFault[R]. USGS Open-File Report： 88--398.

Working Group on California Earthquake Probabilities. 1990.ProbabilitiesofLargeEarthquakesintheSanFranciscoBayRegion，California[R]. USGS Circular: 1053.

Working Group on California Earthquake Probabilities. 1996. Seismic hazards in Southern California: Probable earthquakes， 1994 to 2024[J].BullSeismolSocAm， 85(2): 379--439.

Working Group on California Earthquake Probabilities. 1999.EarthquakeProbabilitiesintheSanFranciscoBayRegion: 2000—2030：ASummaryofFindings[R]. USGS Open-File Report： 99--517.

Working Group on California Earthquake Probabilities. 2003.EarthquakeProbabilitiesintheSanFranciscoBayRegion: 2002—2031[R]. USGS Open-File Report： 214.

Working Group on California Earthquake Probabilities. 2008.TheUniformCaliforniaEarthquakeRuptureForecast，Version2 (UCERF2)[R]. USGS Open-File Report 2007： 1437.

Time-dependent probabilistic seismic hazard analysis methods and its applications based on characteristic earthquake models

(InstituteofGeophysics，ChinaEarthquakeAdministration，Beijing100081，China)

This paper introduces several kinds of characteristic earthquake models, which obey lognormal distribution， normal distribution and Brownian passage-time (BPT)， and then proposes the theory and method of time-dependent probabilistic seismic hazard analysis (PSHA) of characteristic earthquake based on seismic rupture surface model. Finally different characteristic earthquake models are compared through several examples, and the PSHA method of characteristic earthquake are systematically explored. The results indicate that the seismic hazard of time-dependent models of characteristic earthquake in early periods of recurrence cycle is lower than that of time-independent model， and higher than that of time-independent model in later periods. The seismic hazard by using lognormal distribution model is similar to that by BPT model. Before expected recurrence time, the seismic hazard calculated by normal distribution model is similar to the two models mentioned above， but increases quickly near and beyond expected recurrence time.

time-dependent probabilistic seismic hazard; characteristic earthquake; lognormal distribution; Brownian passage-time (BPT) model; seismic rupture surface model

10.11939/jass.2015.06.012.

地震行业科研专项(201408014)资助.

2015-03-04收到初稿， 2015-05-27决定采用修改稿.

e-mail: wujian@cea-igp.ac.cn

10.11939/jass.2015.06.012

P315.5

A

李昌珑, 徐伟进, 吴健, 高孟潭. 2015. 基于特征地震模型含时间的概率地震危险性分析方法及其应用研究. 地震学报, 37(6): 1024--1036.

Li C L, Xu W J, Wu J, Gao M T. 2015. Time-dependent probabilistic seismic hazard analysis methods and its applications based on characteristic earthquake models.ActaSeismologicaSinica, 37(6): 1024--1036. doi:10.11939/jass.2015.06.012.