Secure planar convex hull protocol for large-scaled point sets in semi-honest model①
Sun Maohua(孙茂华)
(*Information School, Capital University of Economics and Business, Beijing 100070, P.R.China)(**School of Computer, Beijing University of Posts and Telecommunications, Beijing 100876, P.R.China)
Secure planar convex hull protocol for large-scaled point sets in semi-honest model①
Sun Maohua(孙茂华)②
(*Information School, Capital University of Economics and Business, Beijing 100070, P.R.China)(**School of Computer, Beijing University of Posts and Telecommunications, Beijing 100876, P.R.China)
Efficiency and scalability are still the bottleneck for secure multi-party computation geometry (SMCG). In this work a secure planar convex hull (SPCH) protocol for large-scaled point sets in semi-honest model has been proposed efficiently to solve the above problems. Firstly, a novel privacy-preserving point-inclusion (PPPI) protocol is designed based on the classic homomorphic encryption and secure cross product protocol, and it is demonstrated that the complexity of PPPI protocol is independent of the vertex size of the input convex hull. And then on the basis of the novel PPPI protocol, an effective SPCH protocol is presented. Analysis shows that this SPCH protocol has a good performance for large-scaled point sets compared with previous solutions. Moreover, analysis finds that the complexity of our SPCH protocol relies on the size of the points on the outermost layer of the input point sets only.
secure multi-party computation, secure multi-party computational geometry (SMCG), secure planar convex hull protocol (SPCH), privacy-preserving point-inclusion protocol (PPPI), semi-honest model
0 Introduction
With the rapid expansion of smart phone and tablet markets, location based service (LBS) becomes more and more popular. LBS uses information on the geographical position of mobile devices and it has a large number of users in social network. Although the LBS applications have significant benefits, some of them reveal privacy of users which may attract security risk. For example, revealing that a master is not at home may be a risk if that information is discovered by thieves. Several technical approaches exist to protect privacy in LBS. One way that formalizes privacy requirements for LBS is done by secure multi-party computation (SMC) protocols. SMC enables mutually suspicious parties to compute a joint function on their private input in a manner that at the end parties know nothing useful and except the result. SMC was introduced by Yao[1], further extended by Goldreich, et al.[2]and other researchers. A series of works have considered the design of more efficient SMC protocols in all kinds of application area.
As a special application area of SMC, SMCG aims to protect the input data in a geometric function computation. SMCG was proposed by Atallah, et al.[3]in 2001. Since its instruction, SMCG has been extensively studied because it can be wildly used in many applications e.g. the privacy issue in LBS applications. In this paper, the SMCG line is followed to protect the privacy information in the geometry function computation, which mainly focuses on two classical SMCG problems, namely PPPI and SPCH.
PPPI problem: Alice has a convex hull P={p0, p1,…,pn}, where p0is the bottom-left point and other points are sorted anticlockwise. Point pican be described as pi=(xi, yi) for 0≤i≤n. Bob has a point q=(m, n). Alice and Bob wish to estimate whether q locates in P without revealing to each other anything intended. Concretely, Alice cannot get the value of q and Bob cannot get anything about P.
SPCH problem: Alice has a point set A,Bob has a point set B. Alice and Bob wish to jointly find the convex hull for these A∪B points. However, neither Alice nor Bob wish to disclose any more information to each other than what can be derived from the result.
PPPI and SPCH are the classical and best studied problems in SMCG. Since their introduction, several techniques have been used to realize PPPI and SPCH protocols. Solutions to PPPI and SPCH include:
Circuit-Based Solutions A naive solution to PPPI or SPCH is using the circuit-based SMC, which is a generic secure computation protocol that allows the secure evaluation of arbitrary functions, expressed as Arithmetic or Boolean circuits. The most classical circuit-based SMC protocol called GMW was introduced by Goldreich, et al[2]. Their solution allows evaluation of arbitrary functions between two parties in the semi-honest model. Improved GMW protocols are proposed in Refs[4-6] recently. Although any polynomial-time multi-party computation can be done by circuit-based solutions, this generic approach is sometimes impractical due to its complexity. Recent research on PPPI and SPCH focuses on finding more efficient privacy-preserving custom algorithms.
Custom PPPI Solutions The first custom PPPI protocol was proposed by Atallah, et al.[3]. Li, et al.[7]proposed an approximate secure multi-party graph inclusion protocol based on Monte Carlo approach and Cantor encoding. Luo, et al.[8]proposed a PPPI protocol to determine whether a point was inside a convex polygon based on the secure cross product protocol; the computational complexity of their protocol is O(tnlogn+tn2) where t denotes the vertex size in the convex hull. Based on additive homomorphic encryption, Liu et al. developed a privacy-preserving point-line relation determination protocol[9]and the computational complexity of their protocol was O(tlogn+tn2). As evaluating the positional relationship between a point and every edge in the convex hull is an intuition to address the PPPI problem, it is found that the computation and communication complexity of the previous protocols using this intuition rely on the vertex size of the input polygon. When the vertex size of the input polygon is large, the previous protocols are less efficient.
Custom SPCH Solutions Lu, et al.[10]provided a SPCH scheme based on Graham algorithm with the computational complexity O(rN3+NlogN) where N denotes the size of the input points set. Based on the Euclid-distance Measure scheme, Wang, et al.[11]presented an approximate solution to the SPCH problem with computational complexity O(N3+N2logN). Hans, et al.[12]constructed an improved SPCH protocol with complexity O(NlogN), unfortunately it was shown in secure in Ref.[13]. Wang, et al. presented a SMC protocol for two party convex hull construction with quadratic communication complexity[14]. In addition, Li, et al.[15]presented a quadratic SMC protocol for approximately three-dimensional convex hulls. Like the existing custom PPPI protocols, it is found find that the complexity of these SPCH protocols relies on the size of input point sets. When the input point sets are large, the protocols are less efficient.
In this work, two effective SMCG protocols including a PPPI protocol and a SPCH protocol are proposed in the semi-honest model. In the PPPI protocol, parties do not need to determine the positional relationship between the input point and every edge in the convex hull; they only need to determine the positional relationship between the input point and one edge which is called the nearest edge. When the size of the input convex hull is large, the proposed protocol is more efficient. The SPCH protocol is designed based on the incremental method. As the parties compute the convex hull of their input point sets respectively in the preprocessing stage, the complexity of the SPCH protocol is only related to the size of the points in the outermost layer. Compared with the previous SPCH protocols, the proposed protocol is faster when the input point sets are large scaled.
Analysis shows that the new protocols are secure in the semi-honest mode. The semi-honest model assumes that parties follow the protocol correctly, and there is no efficient adversary that can extract more information from the transcript of the protocol execution than what is revealed from the output. The scheme secure is not given against malicious adversaries for three reasons. First, the semi-honest model is secure enough when it is hard to tamper the protocol software. This is just right fit for our settings. Second, most of the existing SMCG protocols[7-15]and many advanced SMC protocols[3-18]are proposed in the semi-honest model. The choice of semi-honest model follows the previous work. Third, it is an independent object of interest in SMC to convert protocols in semi-honest model to malicious model[19-28]. These conversions can be used to change the proposed protocols’ secure model if necessary. The security analysis of our protocols uses the definition of the security in semi-honest model given by Goldreich[29]. This analysis method is widely used in SMC protocols.
The paper is organized as follows. Section 1 described the preliminaries. Section 2 depicts the proposed PPPI protocol. The SPCH protocol is presented in Section 3. Conclusion is drawn in Section 4.
1 Preliminaries
1.1 Millionaire protocol
In 1980’s, Yao[1]proposed a constant-round protocol called Millionaire Protocol (MP) to securely compare two private input data owned by the two participants separately. In the proposed protocol, MP is used as the underlying block. In the rest of the paper, MP is used (x, y) to denote the Millionaire Protocol with the input data x and y. The return of MP(x, y) is defined as
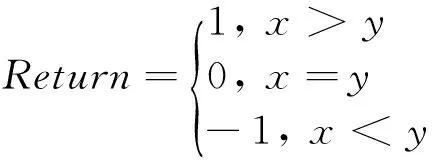
1.2 Homomorphic encryption
1.3 Secure cross product protocol
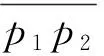
2 PPPI Protocol
2.1 Protocol design
The definition of PPPI problem is described in the Introduction. To avoid evaluating the positional relationship between the q and every edge in P, the following idea is used: in the planar field, three cases exist in the relationship between a convex and a point:
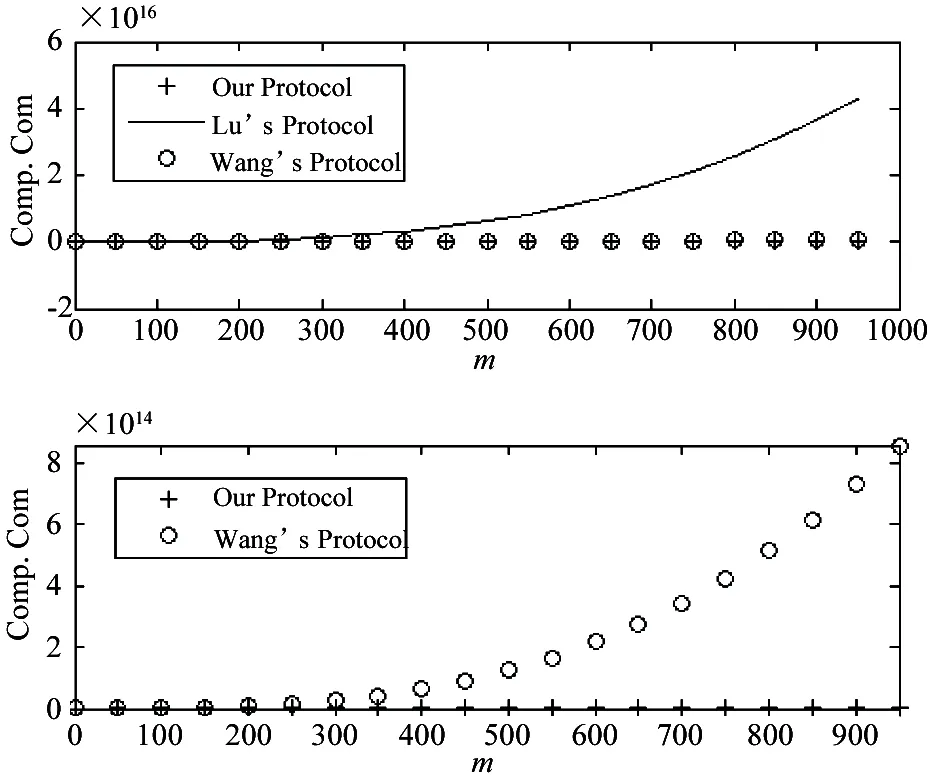
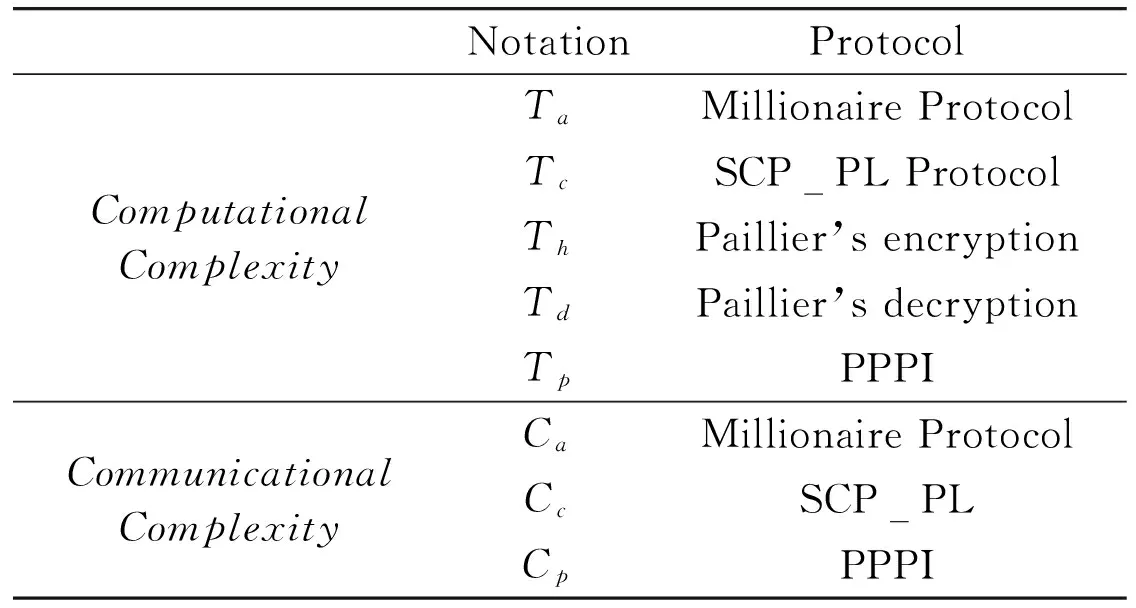
(1) If n Fig.1 Relationship between a point and a convex (2) If n=y0, it is needed to estimate whether q=p0. If q=p0, then point q is the bottom-left point of P. If q≠p0, then q∉P. Such as point B with the convex hull P={p0, p1,…,p4} in Fig.1. (3) If n>y0, it is assumed that q locates between p0pi-1andp0pi. Now, it is needed to estimate the relationship between q and pi-1pi. the nearest edge in the convex hull is called P for point q. If q locates at the left side of pi-1pi, then q∈P. Such as point D with the convex hull in Fig.1. When q locates at the right side of pi-1pi, q∉P, such as point C with convex hull P={p0, p1,…,p4} in Fig.1. Based on the idea above, firstly MP and additive homomorphic encryption scheme are used to find the nearest edge in P for q; Secondly, SCP_PL is used to determine the relationship between q and the nearest edge which reflect the relationship between q and P. The PPPI protocol is described in Table 1. In the rest of our paper, Ai^Bidenotes that Alice and Bob compute the function jointly in step i; Ai|Bidenotes that Alice and Bob compute the function seperately in step i; Aidenotes that Alice computes the function alone in step i. Table 1 PPPI Protocol 2.2 Security analysis Theorem 1 Assuming the underlying millionaire protocol, homomorphic encryption scheme and SCP_PL protocol are secure in semi-honest model, the proposed PPPI protocol securely evaluates the relationship between the input point and convex hull in the presence of semi-honest adversaries. Proof: As the underlying millionaire protocol is secure in semi-honest model, our protocol is secure if n≤y0. If n>y0, the security of our protocol is analyzed as following: Alice inputs the point set P={p0, p1,…,pn}, Bob inputs the point set q=(m,n). The protocol outputs outputΠ=t where t=True refers to q∈P and t=False refers to q∉P. Bob’s view The view of Bob during the execution of π is E′(r′m-r′x0)=[E(-x0)]r′E(r′m) E′(r′n-r′y0)=[E(-y0)]r′E(r′n) As the underlying homomorphic encryption scheme, millionaire protocol and SCP_PL protocol are secure in semi-honest model, the conclusion is that Thus it is concluded the simulated view is distinguishable from the real view: The same simulator can be created for Alice. 2.3 Algorithm complexity In SMCG, many protocols use underlying building blocks without specifying the protocol detail. Notations defined in Table 6 is used to compare the complexity. To compare the computational complexity concretely, the underlying protocols are referred as follows: Paillier’s cryptosystem is used as the additive homomorphic encryption scheme; the protocol presented in Ref.[18] is used to solve the millionaire problem; Luo’s solution[30]is used as the underlying SCP_PL protocol. The communicational complexity is concluded in Table 2 (t is the vertex size in the convex hull).It shows that the complexity of protocols in Refs[8,9] relies on the vertex size of the convex hull while the proposed protocol is not. When the number of the vertex in the convex hull is huge, our protocol is much better than the previous protocols. Table 2 Algorithm complexity 3.1 Protocol design To reduce the interactive computation, Alice and Bob evaluate the convex hull of his/her point set locally at the preprocessing phase. This method is also used in the previous works[32,33]. M={m1,…,mk} and N={n1,n2,…,nt} stand for the vertex set of convex hull of Alice’s and Bob’s point set respectively. Now, Alice and Bob can use incremental method to evaluate the convex hull of set M and N. When evaluating the convex hull of point p and convex hull P, there are two cases as shown in Fig.2: (1) If p locates in P, the new convex hull remains to be P. The SPCH protocol is described in Table 3. Table 3 SPCH protocol 3.2 Security analysis Theorem 2 Assuming the underlying protocol is secure in semi-honest model, the SPCH protocol securely evaluates the convex hull of the input point sets in the presence of semi-honest adversaries. The same simulator can be created for Alice. 3.3 Algorithm complexity In the processing stage, PPPI protocol is called for m times. For the worst case that all the vertexes of Alice’s convex hull locate at the outside of Bob’s convex hull, SCP_PL Protocol is used for mn times. So the computational complexity of the proposed protocol is mnTc+mTp, and the communication complexity is mCp+mnCc. The notations used here are defined in Appendix B. The computational and communicational complexity comparison of Lu’s, Wang’s and the proposed protocol are shown in Table 4. It shows that the complexity of protocols in Refs[10,11] relies on the input point set size. The proposed protocol’s complexity only relies on the size of the input points’ convex hull vertex set. So, when the points in the two party’s input point set are dense, the proposed protocol is more efficient than the previous works. Table 4 Algorithm complexity (M and N denote the set size of Alice and Bob. m and n denote the size of Alice’s and Bob’s convex hull vertex set.) To compare the complexity visually, the computational complexity of Lu’s, Wang’s and the proposed protocol are charted in Fig.3. For the sake of comparison, it is assumed that M=N, m=n, M=100m, r=50. The same conclusion can be got with the theoretical analysis above. Privacy-preserving point-inclusion and secure planar convex hull are the classical problems in SMCG. In this work, a novel PPPI protocol has been designed based on the classic homomorphic encryption and secure cross product protocol. Analysis shows that novel PPPI is highly efficient because the complexity is not related to the vertex size of the convex hull. Based on the novel PPPI protocol, an effective SPCH protocol has been presented. Analysis finds that the complexity of this SPCH protocol only relies on the size of the points in the outermost layer of the input point sets, and it has a good performance for large-scaled point sets compared with the previous solutions. Fig.3 Comparisons of Different SPCH protocols The proposed protocols are secure in semi-honest model, and the security of the protocols has been demonstrated by Goldreich method. The real world implementation and protocols secure against malicious adversary will be the goal in the future. [ 1] Yao A C. Protocols for secure computations. In Proceedings of 23th Annual IEEE Symposium on Foundations of Computer Science, Chicago, USA,1982. 160-164 [ 2] Goldreich O, Micali S, Wigderson A. How to play any mental game. In: Proceedings of the 19th Annual CAN Symposium on Theory of Computing, 1987. 218-229 [ 3] Atallah M J, Du W L. Secure multi-party computational geometry. International Workshop on Algorithms and Data Structures, 2004, 2125: 165-179 [ 4] Choi S G, Hwang K W, Kaza J, et al. Secure multi-party computation of Boolean circuits with application to privacy in online marketplaces. In: Proceedings of the Cryptographer’s Track at the RSA Conference on Topics in Cryptology, San Francisco, USA, 2012. 416-432 [ 5] Nielsen J B, Nordholt P S, Orlandi C, et al. A new approach to practical active-secure two-party computation. In: Proceedings of the Advances in Cryptology-CRYPTO 2012, volume 7417 of LNCS, 2012. 681-700 [ 6] Schncider T, Zohner M. GMW vs Yao? Efficient secure two-party computation with low depth circuits. In: Proceedings of the Financial Cryptography and Data Security, volume 7859 of LNCS, 2013.275-292 [ 7] Li S D, Si T G, Dai Y Q. Secure multi-party computation of set-inclusion and graph-inclusion. Journal of Computer Research and Development,2005,42(10):1647-1653 [ 8] Luo Y L, Huang L S, Zhong H, et al. A secure protocol for determining whether a point is inside a convex polygon. Chinese Journal of Electronic,2006,15(4):578-582 [ 9] Liu W, Luo S S, Chen P. Privacy-preserving point-line relation determination protocol and its application. Journal of Beijing University of Posts and Telecommunications,2008,31(2): 72-75 [10] Lu S F, Luo Y L. Privacy-preserving in graham algorithm for finding convex hulls.Computer Engineering and Applications, 2008,44(36):130-133 [11] Wang Q, Huang L S. Privacy- preserving protocols for finding the convex hulls. In: Proceedings of the 3rd International Conference on Availability, Reliability and Security, Barcelona, Spain, 2008.727-732 [12] Hans S, Addenpalli S C, Gupta A, et al. On privacy preserving convex hull. In: Proceedings of the International Conference on Availability, Reliability and Security, Los Alamitos, USA,2009.187-192 [13] Eppstein D, Goodrich M T, Tamassia R. Privacy-preserving data-oblivious geometric algorithm for geographic data. In: Proceedings of the 18th ACM SIGSPATIAL International Conference Advances in Geographic Information Systems, San Jose, USA, 2010. 13-22 [14] Wang Q, Zhang Y. A convex hull algorithm for planar point set based on privacy protecting. In: Proceedings of the International Workshop on Education Technology and Computer Science, Wuhan, China, 2009. 434-437 [15] Li D, Huang L S, Yang W, et al. A practical three-dimensional privacy-preserving approximate convex hulls protocol. In: Proceedings of the 2008 Japan-China Joint Workshop on Frontier of Computer Science and Technology, Nagasahi, Japan, 2008.17-23 [16] Pinkas B, Schneider T, Zohner M. Faster private set intersection based on OT extension. In: Proceedings of the 23rd USENIX Security Symposium(USENIX Security’14), San Diego, USA, 2014. 447 [17] Mohassel P, Sadeghian S. How to hide circuits in MPC an efficient framework for private function evaluation. In: EUROCRYPT, volume 7881 of LNCS, 2013.557-574 [18] Gennaro R, Hazay C, Jeffrey S. S. Automata Evaluation and Text search protocols with simulation based security. In Public Key Cryptography, volume 6056 of LNCS, 2010.332-350 [19] Barni M, Failla P, Kolesnikov V, et al. Secure evaluation of private linear branching programs with medical applications. In: Proceedings of the 14th European Symposium on Research in Computer Security, volume 5789 of LNCS, 2009. 424-439 [20] Katz J,Ostrovsky R. Round-optimal secure two-party computation. In: CRYPTO, volume 3125 of LNCS, 2004.335-354 [21] Pass R. Bounded-concurrent secure multi-party computation with a dishonest majority. In: Proceedings of the 36th Annual ACM Symposium on Theory of Computing, 2004. 232-241 [22] Katz J,Ostrovsky R, Adam S. Round efficiency of multi-party computation with a dishonest majority. In EUROCRYPT, volume 2656 of LNCS, 2003. 578-595 [23] Damgård I, Ishai Y. Constant-round multiparty computation using a black-box pseudorandom generator. In CRYPTO, volume 3621 of LNCS, 2005. 378-394 [24] Aumann Y, Lindell Y. Security against covert adversaries: efficient protocols for realistic adversaries. In: Proceedings of the 4th Theory of Cryptography Conference, volume 4392 of LNCS, 2007.137-156 [25] Goyal V , Mohassel P , Smith A. Efficient two party and multi party computation against covert adversaries. In EUROCRYPT, volume 4965 of LNCS, 2008. 289-306 [26] Lindell Y, Pinkas B. An efficient protocol for secure two-party computation in the presence of malicious adversaries. In EUROCRYPT, volume 4515 of LNCS, 2007. 52-78 [27] Malkhi D, Nisan N, Pinkas B, et al. Fairplay - a secure two-party computation system. In: Proceedings of the 13th Conference on USENIX Security Symposium, volume 13, 2004. 09-13 [28] Sella J B, Orlandi C. LEGO for two-party secure computation. In Theory of Cryptography Conference, volume 5444 of LNCS, 2009.368-386 [29] Goldreich O. The Foundations of Cryptography-Volume 2, Basic Applications. Cambridge University Press, 2004 [30] Luo Y L, Huang L S, Wei J J, et al. Privacy-preserving cross product protocol and its application. Chinese Journal of Computers,2007,30(2):248-254 [31] Paillier P. Public-key cryptosystems based on composite degree residuosity classes. In: EUROCRYPT, volume 1592 of LNCS,1999. 223-238 [32] Nielsen J B, Nordholt P S, Orlandi C, et al. A new approach to practical active-secure two-party computation. In CRYPTO, volume 7417 of LNCS, 2012. 681-700 [33] Damgard I, Pastro V, Smart N,et al. Multiparty computation from somewhat homomorphic encryption. In CRYPTO, volume 7417 of LNCS, 2012. 643-662 Appendix A Table 5 Intermediate variables among SCP_PL Appendix B Table 6 Notation used in the paper Sun Maohua, born in 1986. She received her Ph.D degree from Beijing University of Posts and Telecommunications in 2013. She also received her Bachelor’s degree from Shandong University in 2008. Her research interests include secure multi-party computation and information security. 10.3772/j.issn.1006-6748.2015.04.014 ①Supported by the Young Scientists Program of CUEB (No. 2014XJQ016, 00791462722337), National Natural Science Foundation of China (No. 61302087), Young Scientific Research Starting Foundation of CUEB and Improve Scientific Research Foundation of Beijing Education. ②To whom correspondence should be addressed. E-mail: starjingxiang@sina.com Received on Oct. 23, 2014*, Zhu Hongliang**, Li Qi**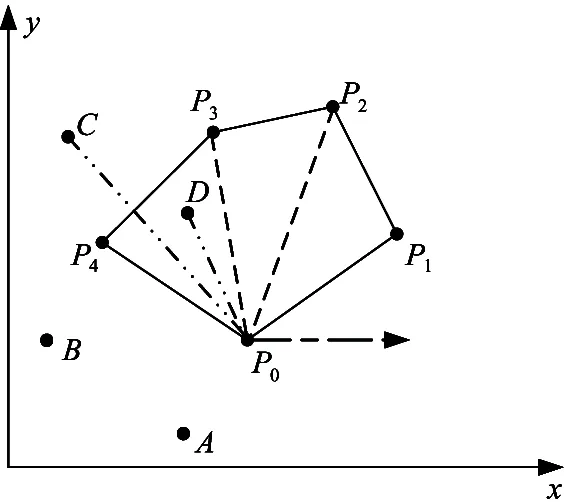

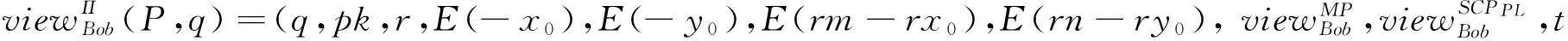
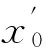
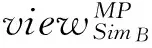
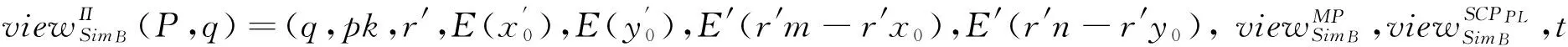

3 Secure planar convex hull protocol

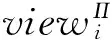

4 Conclusion
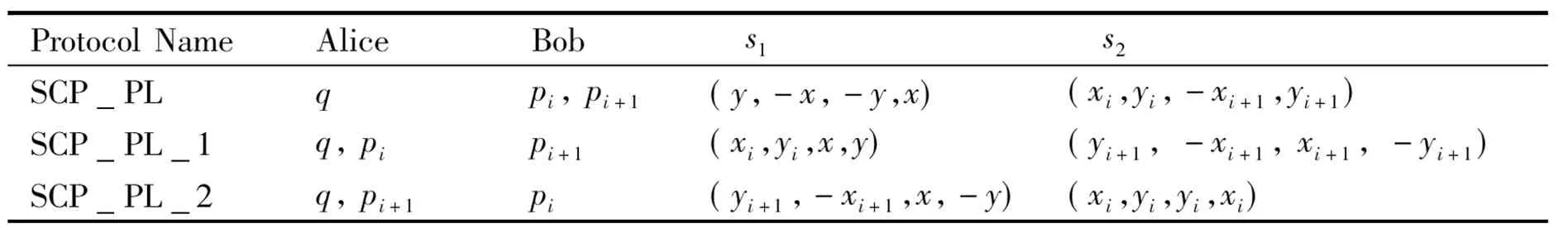
 High Technology Letters2015年4期
High Technology Letters2015年4期
- High Technology Letters的其它文章
- Motion mechanism analysis of two contacting rollers①
- Two-stage DOA estimation method for passive radar based on sparse representation①
- Study and application of vibrating wire strain gauge in monitoring cable tension of FAST cable-net①
- Service optimization in programmable cloud network①
- Design of bilayer lengthened LDPC codes over expanded graph for relay channels①
- Effect of laser heating on the microstructure and hardness of TRIP590 advanced high strength steel used for roll forming①
