充泥过程中土工织物管袋的受力和变形分析

陈 亮，雷国辉，赵仲辉

(1.河海大学岩土力学与堤坝工程教育部重点实验室，江苏南京 210098;2.河海大学岩土工程科学研究所，江苏南京 210098;3.长江新能源开发有限公司，上海 200001)

长条形土工织物管袋充泥筑堤、围埝及护岸技术在水利和海岸工程中得到越来越广泛的应用［1-6］，该技术已成功应用于我国连云港［2］、黄骅港［7］和天津港［8-9］工程建设。在土工管袋设计中，管袋的拉力和变形形状是需要考虑的重要因素［10］。针对土工管袋的受力和变形问题已经提出了一些相对简便实用的解析计算方法，通常是将其假设为刚性水平地基上的平面应变问题，忽略管袋的自重和拉伸变形，在已知管袋横截面周长和底部或顶部压力的条件下，通过平衡方程和几何约束条件，采用不同的数学方法或考虑不同的工况，求解管袋的拉力、充填高度和形状［10-22］。通过文献分析发现，管袋受力和变形问题的支配方程是非线性偏微分方程，管袋拉力将随充填过程中管袋的变形而非线性增长，而现有的解析计算方法主要给出了在特定泵压充填压力条件下管袋拉力和变形的解答，对于在充填过程中，充填压力随充填速率或充填时间变化情况下管袋拉力和变形变化规律的分析尚欠深入。为此，笔者针对刚性水平地基上的充泥土工织物管袋，采用Plaut等［13］运用无量纲化方法建立的特定泵压充填压力条件下的支配方程，考虑充填过程中充填压力随充填速率的变化，以及自由充填工况，推导了充填过程中管袋受力和变形的解析解答，分析管袋拉力和形状在充填过程的变化规律，并探讨不同管袋横截面周长情况下的合理充填体积或充填高度问题。

图1 刚性水平地基上的管袋示意图Fig.1 Sketch of a geosynthetic tube on rigid horizontal foundation

1 管袋的受力和变形解答

1.1 假设条件与控制方程

为推求刚性水平地基上充泥管袋的受力和变形解答，考虑问题的复杂性和求解难度，进行如下假设:(a)所研究问题为平面应变问题;(b)管袋不可拉伸、无弯曲刚度、不计自重，在充填过程中不透水;(c)管袋内部充填泥浆，且在充填过程中保持为液态;(d)管袋与泥浆、地基之间的摩擦力忽略不计。

建立坐标系如图1所示，坐标原点设置于管袋与地基接触和分离的临界点位置(图中H为管袋高度，L为管袋横截面周长，C为管袋与地基的接触长度，S为管袋与地基非接触部分即自由变形部分的弧长，θ为管袋任意一点切线方向与X轴正向的夹角)。

图2 管袋任一微段的受力分析示意图Fig.2 Force diagram of geosynthetic tube at an arbitrary infinitesimal segment

如图2所示，取垂直于横截面的纵向单位长度管袋上任一微段做受力分析。图2中T为管袋横截面的周向拉力，PA为管袋上任一微段处所受内部泥浆压力，则PA=P-ρgY，P为管袋底部与地基接触部分受到的泥浆压力，ρ为管袋内部充填泥浆的密度，g为重力加速度。

根据受力平衡PAdS=2Tsin(dθ/2)=Tdθ，得

另由几何关系可知管袋受力和变形的控制方程为

参考Plaut等［13］的方法，引入下列无量纲参数:

式中:p——管袋底部压强的无量纲数;τ——管袋周向拉力的无量纲数;V——垂直于管袋横截面方向即纵向单位长度管袋的体积。

控制方程(1)～(3)可转换为

值得注意的是，式(5)仅在p＞y即P＞ρgY时才有意义。由于管袋充填时Y的最大值为充填高度H，因此式(5)要求p＞h即P＞ρgH，这种工况对应于泵压充填即管袋顶部压力不为零的工况。而管袋在充填过程中，初期将在泥浆自重作用下使其膨胀，此时对应于自由充填即管袋顶部压力为零的工况，式(5)及其现有的相应解答并不适用;充填后期当管袋膨胀到一定高度后，只有增加泵压即对应于管袋顶部压力不为零的工况，才能使管袋继续充填和膨胀，此时式(5)方才适用。为此，以下将区分这2种工况分别对管袋的受力和变形进行求解。

1.2 管袋顶部压力不为零即泵压充填时解答

将管袋划分为足够小的微段，求解式(5)～(7)可以得到任一微段的形状方程为

式中:α、β——各微段的始末端。

令式(9)中 θα=0，θβ=π，此时的y值即为管袋高度h，则

令式(8)中θα=0，θβ=2π，此时x的绝对值为管袋底部与地基的接触长度c，即

由管袋的整体受力平衡，即管袋底部与地基接触面上的法向压力与充填泥浆的重力相等，可得ρgV=PC，则根据式(4)可得v=pc，将式(12)代入后即可求出单位长度管袋的体积为

由图1可知，当θα=0、θβ=2π时，s为管袋与地基非接触部分的弧长，c为管袋底部与地基接触部分的长度，因此，根据管袋周长的无量纲值为1可得此时s+c=1。将式(10)和式(12)代入后可得

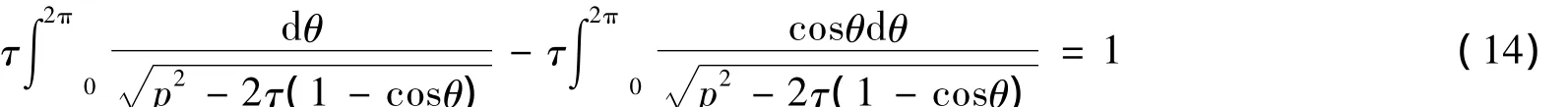
设泥浆充填速率为qf，充填时间为t，则V=qft，由式(4)可得v=qft/L2，则由式(13)可得

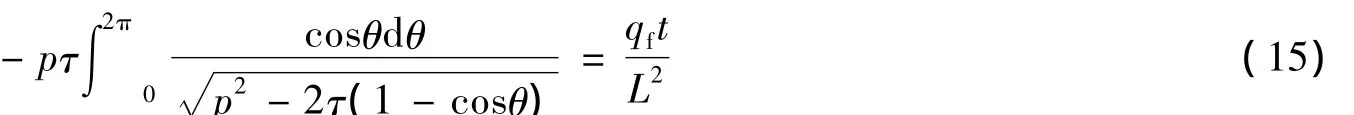
某一时刻t，对于给定的管袋周长及qf，联立式(14)和(15)即可组成含有2个未知数p和τ的方程组。求解此方程组即可得到p和τ，进而分别由式(11)～(13)可得到h、c、v。将求得的p和τ代入式(8)～(10)即可求得管袋在此充填时刻的形状。

1.3 管袋顶部压力为零即自由充填时解答

由式(11)可知，只有当τ＜p2/4时才可用式(14)和式(15)进行求解。对于充填初期管袋顶部压力为零的工况，此时p=h即τ=p2/4，管袋的受力和变形需另行求解。在这种状态下，管袋为扁平状，顶部基本水平，横截面形状近似如图3所示。为简便起见，假设管袋的形状为矩形，根据管袋周长的无量纲数为1可知

此时 2h+2c=1，即

由p=h可得

由v=pc可得

再由v=qft/L2可得

图3 充填初期管袋的形状Fig.3 Shape of geosynthetic tube at early stage of filling

另外，根据式(20)可知，对于给定的管袋周长和充填速率，由式(19)可求出管袋顶部压力为零时任意充填时刻的p，再由式(16)、式(17)和式(20)可求出对应的h、c以及τ。

1.4 临界充填高度及求解方法

从管袋充填时刻t=0起，管袋高度逐渐增加，将分别经历管袋顶部压力为零即p=h阶段以及管袋顶部压力不为零即p＞h阶段。定义管袋在泥浆充填过程中从h=p达到h＜p时的h值为临界充填高度hc。笔者采用Mathematica软件来确定hc值，方法如下:(a)假设某一p值，由式(14)求解τ;(b)若 τ-p2/4/τ＞10-4，则重新选取较小的p值，代入式(14)求解τ;(c)重复上述步骤直至 τ-p2/4/τ≤ 10-4，并记录p值。

计算结果如图 4所示，可以看出:当p=0.1时，

τ-p2/4/τ=0.98×10-4，即式(14)与式(20)这2 种求解管袋拉力方法的结果相对误差小于10-4。因此，此时的管袋高度即为临界高度，其无量纲值hc=p=0.1，由式(20)可知对应的管袋周向拉力的无量纲数τc=0.0025，由式(18)可知对应的管袋充填体积vc=0.04，由式(19)可求出给定管袋周长和充填速率下达到临界充填高度的充填时间tc=0.04L2/qf。

综上可知，当t≤tc时h=p，管袋的受力和变形按1.3节的解答进行求解;当t＞tc时h＜p，管袋的受力和变形按1.2节的解答进行求解。将求得的无量纲解答v、p、t、h、c代入式(4)中，即可求出对应的有量纲的解答。

图4 τ与p2/4的相对误差随底部压强的变化Fig.4 Variation curve of relative error between τand p2/4 against p during filling process

2 计算结果及分析

采用Mathematica软件进行求解计算。假定土粒相对密度Gs=2.65，充填泥浆含水率w=190%，则袋内充填泥浆的饱和密度ρs=1273 kg/m3，假定泥浆充填速率qf=0.145 m3/min，选取2种不同横截面周长的管袋L=8 m和L=10 m，对其受力与变形情况进行对比分析。

2.1 充填过程中管袋的形状

充填过程中管袋的变形形状如图5所示。由图5可见，采用本文解答可以模拟充填过程中管袋的形状变化。充填初期，管袋为扁平状;充填后期，随着泥浆的持续充入，管袋最终将变为圆柱状(因为在相同的横截面周长情况下，圆形的横截面积最大)。然而，管袋从扁平状变化到圆柱状需要充填压力作为保障，即需要增加泵压才能实现。

2.2 充填过程中管袋的受力和变形

图6所示为泥浆充填速率qf=0.145m3/min、管袋横截面周长为L=8m和L=10m时，充填过程中管袋底部压力P、管袋拉力T、管袋底部与地基接触长度C以及管袋高度H随时间的变化过程。图中实心圆点代表p=h=0.1(即管袋达到其临界充填高度hc)对应的值。

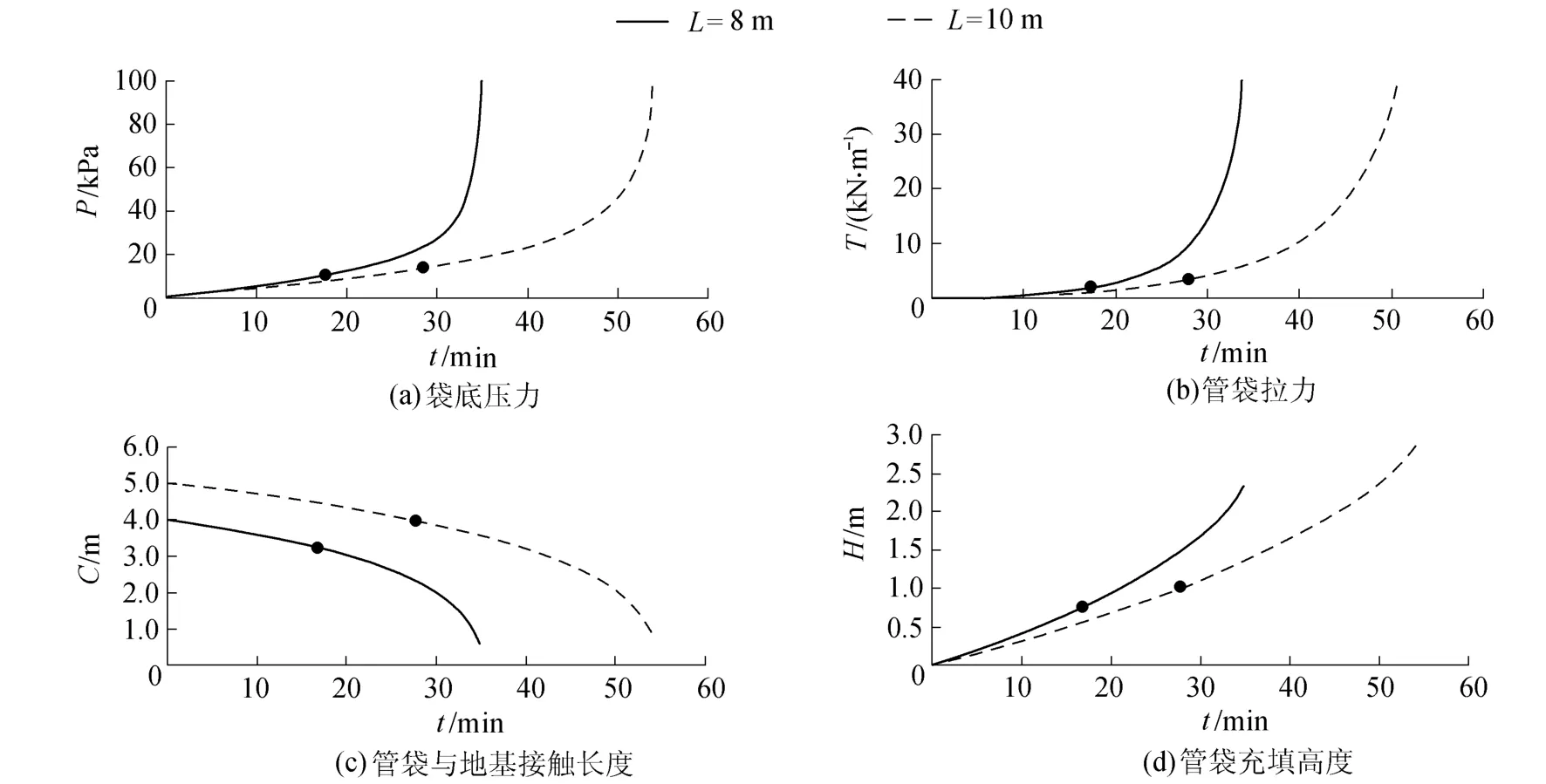
图6 充填过程中管袋的受力与变形Fig.6 Force and deformation of geosynthetic tube during filling process

从图6可以看出，管袋在达到临界高度前，P、H、C基本都随着充填时间线性变化。而当管袋达到临界充填高度之后继续充填时，所需的P将随着充填时间非线性增长，增长速率迅速增大，但H的增长却相对缓慢。显然，在管袋达到临界高度后，只有大幅度增加泵压才能使管袋继续充填，但充填高度的增长却相对有限。

同时可以看出:T在整个充填过程中都随着充填时间非线性增长，管袋在达到临界高度前T增长相对缓慢;当管袋达到临界高度后，继续充填则T将显著增大。不同的qf及不同L的管袋均表现出与上述情况类似的变化特征。管袋材料选型时，可根据管袋拉力的计算值确定满足抗拉强度要求的土工织物材料。

由上述分析可知，在实际工程中通过增加泵压以增加充填体积将大幅度增加施工成本，而充填体积的增加却是有限的，性价比差。因此，hc可为管袋的设计提供参考。根据无量纲化方法确定的结果可知，h=hc=0.1(即H=0.1L)时，τ=0.0025，即T=0.0025ρgL2，对应的v=0.04，即V=0.04L2。

3 结 语

a.考虑充填速率和充填时间的作用影响，推导了管袋在整个充填过程中从自由充填到泵压充填情况下的拉力、充填高度、形状和体积的求解方法。

b.确定了从自由充填到泵压充填的临界充填高度为0.1倍的管袋周长L，对应的管袋拉力为0.0025ρgL2，单位长度充填体积为0.04L2，充填时间为0.04L2/qf。

c.在自由充填阶段，管袋拉力增长缓慢。但在管袋充填达到临界充填高度之后需要显著增加泵压才能使管袋继续充填，而充填高度和充填体积的增加却不明显;充填高度和充填体积与充填压力之比显著减小，充填效率明显降低。

［1］朱朝荣，束一鸣，姜俊红，等.管袋堤坝在水流作用下的稳定性模型试验［J］.河海大学学报:自然科学版，2008，36(3):333-336.(ZHU Chaorong，SHU Yiming，JIANG Junhong，et al.Experiment on the stability of geotube embankments in river current［J］.Journal of Hohai University:Natural Sciences，2008，36(3):333-336.(in Chinese))

［2］范公俊，贾延权，王艳红.几种围堰施工技术在连云港滩涂区的应用［J］.水利水电科技进展，2011，31(1):62-65.(FAN Gongjun，JIA Yanquan，WANG Yanhong.Application of several kinds of cofferdam construction techniques in tidal flat of Lianyungang［J］.Advances in Science and Technology of Water Resources，2011，31(1):62-65.(in Chinese))

［3］杨智，袁磊，李淼，等.充泥管袋和模袋混凝土在堤防中的应用［J］.水利水电科技进展，2000，20(2):44-46.(YANG Zhi，YUAN Lei，LI Miao，et al.Application of sacked soil and fabric-wrapped concrete to dykes［J］.Advances in Science and Technology of Water Resources，2000，20(2):44-46.(in Chinese))

［4］CHU Jian，GUO Wei，YAN Shuwang.Geosynthetic tubes and geosynthetic mats:analyses and applications［J］.Geotechnical Engineering Journal of the SEAGS＆ AGSSEA，2011，42(1):56-65.

［5］LAWSON CR.Geotextile containment for hydraulic and environmental engineering［J］.Geosynthetics International，2008，15(6):384-427.

［6］LEE E C，DOUGLAS R S.Geotextile tubes as submerged dykes for shoreline management in Malaysia［J］.Geotextiles and Geomembranes，2012，30:8-15.

［7］马燕.大型充泥袋结构在黄骅港一期工程引堤工程中的应用［J］.港工技术，1999(4):21-24.(MA Yan.Application of big filled bags to the approach embankment of phase one project，Huanghua Port［J］.Port Engineering Technology，1999(4):21-24.(in Chinese))

［8］YAN Shuwang，CHU Jian.Construction of an offshore dike using slurry filled geotextile mats［J］.Geotextiles and Geomembranes，2010，28(5):422-433.

［9］YEE T W，LAWSON C R，WANG Z Y，et al.Geotextile tube dewatering of contaminated sediments，Tianjin Eco-City，China［J］.Geotextiles and Geomembranes，2012，31:39-50.

［10］LESHCHINSKY D，LESHCHINSKY O，LING H I，et al.Geosynthetic tubes for confining pressurized slurry:some design aspects［J］.Journal of Geotechnical Engineering，ASCE，1996，122(8):682-690.

［11］闫玥，闫澍旺，邱长林，等.土工织物充灌袋的设计计算方法研究［J］.岩土力学，2010，31(1):327-330.(YAN Yue，YAN Shuwang，QIUChanglin，et al.Design and calculation methods of geotextile tubes filled with soil slurry［J］.RocKand Soil Mechanics，2010，31(1):327-330.(in Chinese))

［12］邱长林，闫玥，闫澍旺.泥浆不均匀时土工织物充填袋特性［J］.岩土工程学报，2008，30(5):760-763.(QIU Changlin，YAN Yue，YAN Shuwang.Behavior of geotextile bags filled with non-uniform silty slurry［J］.Chinese Journal of Geotechnical Engineering，2008，30(5):760-763.(in Chinese))

［13］PLAUT R H，SUHERMAN S.Two-dimensional analysis of geosynthetic tubes［J］.Acta Mechanica，1998，129(3/4):207-218.

［14］KAZIMIEROWICZ K.Simple analysis of deformation of sand-sausages［C］//The International Geotextile Society.Proceedings of the 5th International Conference on Geotextiles.Geomembranes and Related Products.Singapore:Southeast Asian Chapter of the International Geotextile Society，1994:775-778.

［15］NAMIASV.Load-supporting fluid-filled cylindrical membranes［J］.Journal of Applied Mechanics，1985，52(4):913-918.

［16］WANG C Y，WATSON L T.The fluid-filled cylindrical membrane container［J］.Journal of Engineering Mathematics，1981，15(2):81-88.

［17］LIU G S，SILVESTER R.Sand sausages for beach defence work［C］//The Institution of Engineers，Australia.Proceedings of the 6th Australasian Hydraulics and Fluid Mechanics Conference.Australia.Perth:University of Western Australia，1977:340-343.

［18］LIU Weichao，ZHANG Yiping，LI Tao，et al.Simulation of filling construction of permeable geosynthetic tubes［J］.Journal of Zhejiang University-Science A:Applied Physics＆ Engineering，2010，11(6):425-431.

［19］MALIKJ，SYSALA S.Analysis of geosynthetic tubes filled with several liquids with different densities［J］.Geotextiles and Geomembranes，2011，29(3):249-256.

［20］刘伟超，张仪萍，杨艳，等.任意对称刚性地基上土工管袋充填形状和受力分析［J］.浙江大学学报:工学版，2011，45(7):1308-1313.(LIU Weichao，ZHANG Yiping，YANG Yan，et al.Shape and mechanical behavior of geotubes on rigid foundation with symmetry arbitrary shape［J］.Journal of Zhejiang University:Engineering Science，2011，45(7):1308-1313.(in Chinese))

［21］PLAUT R H，STEPHENST C.Analysis of geotextile tubes containing slurry and consolidated material with frictional interface［J］.Geotextiles and Geomembranes，2012，32:38-43.

［22］GUO Wei，CHU Jian，YAN Shuwang，et al.Geosynthetic mattress:analytical solution and verification［J］.Geotextiles and Geomembranes，2013，37:74-80.