基于神经二部分裂结构的多智能体WSNs数据融合算法*

屠雄刚,陈 军,张长江

(1.浙江师范大学数理与信息工程学院,浙江 金华 321004;2.浙江工业职业技术学院设计与艺术学院,浙江 绍兴 312000)



基于神经二部分裂结构的多智能体WSNs数据融合算法*

屠雄刚1,2*,陈 军2,张长江1

(1.浙江师范大学数理与信息工程学院,浙江 金华 321004;2.浙江工业职业技术学院设计与艺术学院,浙江 绍兴 312000)

为进一步提高无线传感器网络WSNs(Wireless Sensor Networks)使用寿命,从提高算法数据融合效率角度出发,提出一种神经二部分裂结构的多智能体WSNs数据融合算法。首先,根据神经结构的主干与枝干承载信息量不同的原理,选取主干、枝干通讯链路并赋予较大能量,并给出主、辅中心节点选取方法;其次,设计了基于LMS的自适应加权融合算法,分别针对节点层级、枝干中心层级和主干中心层级进行逐层处理,实现了对神经二部分裂结构的数据融合;最后,通过与两种已有算法进行仿真对比,显示本文算法在Sink节点接收数据包,能耗等指标上均具有优势,验证了算法有效性。

无线传感器网络;多智能体;神经二部分裂;数据融合

无线传感器网络(WSNs)是基于能量驱动的,因此能量约束是限制网络使用寿命的主要因素[1～2]。为突破或更好的利用能量资源,相关学者给出了不同的研究方向:

文献[3]提出一种联合路由优化和无损数据融合的WSNs网络寿命延长算法;文献[4]采用一种递归平滑函数进行优化,并考虑时空特性,实现数据融合的自适应机制;文献[5]提出一种冗余消除的相邻传感器节点数据融合技术;文献[6]提出一种优化的贝叶斯估计多传感器数据融合方法,等。

上述算法都在提高数据融合算法性能角度,降低和平衡能耗,并延长WSNs网络使用寿命。此研究方向成果较多且较为成熟,但是在WSNs网络布局方面的文献相对较少,例如文献[7]提出的基于车轮形状的WSNs网络布局等。此文献可看作是一种二级模式下的网络布局,分为Sink节点和网管节点。

为进一步提高算法性能,设计一种神经二部分裂结构的多智能体WSNs数据融合算法NBMA-WSNs(Neural Bipartitions structure based Multiagent WSNS fusion Algorithm),实现信息传输的三级网络模式。

1 算法框架描述

1.1 神经二部分裂结构

人体神经结构(nervous system)是生命体内起主导的感觉系统,主要由中枢系统和周围系统组成[8]。中枢神经系统包括脑和脊髓,周围神经系统主要由31对脊神经和12对脑神经组成,分布在人体各处,负责感知和连接中枢神经和人体组织的作用,保证中枢系统既可感知内外变化,又可实时调整人体动作和各脏器功能,实现人体的统一与适应性功能。简单的神经网络结构为类似于二叉树性质的简化结构,这里称之为神经二部分裂结构,如图1所示。

通过分析人体神经网络结构,如图1可知具有如下特点:一是脑神经负责全身神经信号的接收与处理,需要较大计算量并且耗费大量的能量,脊髓神经(Sink节点)与脑神经直接相连;二是脊髓神经负责连接全身神经与脑神经,并负责将信号传导给脑神经,消耗相对较多的能量,局部神经元中心(主中心节点)与脊髓神经(Sink节点)直接相连;三是全身神经负责人体感知,处理数据简单,耗费能量较少,当网络过大时,增加二级局部神经元中心(辅中心节点)管理分散神经元。经过分析可知,若无线传感器网络结构采用上述信号传导和能量分配方法,可取得较好的能量使用效率和网络使用寿命。

图1给出的神经二部分裂WSNs数据融合路由简化结构,从图中不难看出,该算法结构能够顺利执行需要解决一下问题:①适合计算机处理的多智能体框架的构建;②主、辅中心节点的选取;③节点信息融合算法。下面将主要围绕上述问题进行阐述。

1.2 多智能体框架

图2(a)为Sink节点Agents框架,主要组成部分有:

①Sink管理Agent(SMA),为一静态的Agent,用来监测临近节点信息,利用GPS信息计算参考方向,上传并更新Sink黑板中的数据融合。负责计算相邻节点的权重系数和欧氏距离,来选择最近的主干中心节点。SMA通过全局主中心阈值Dmth和局部辅中心阈值Dlth,由用户在数据融合中心触发;

②全局主中心点选择Agent(MCSA),是一个由SMA基于相邻节点之间的权重系数和欧氏距离触发的移动Agent。MCSA作用是负责神经二部分裂结构主中心的选择。并根据主神经(轴突)角阈值,辅神经(树突)角阈值来更新辅主中心点,直到到达区域边界处;

③Sink黑板(SBB),是可由SMA和MCSA读取和更新的知识库,存储有节点连接信息:节点ID、剩余能量、偏角,邻近节点数,信号强度,区域位置,历史数据融合,主神经角度阈值,辅神经角度阈值,接收时间等。

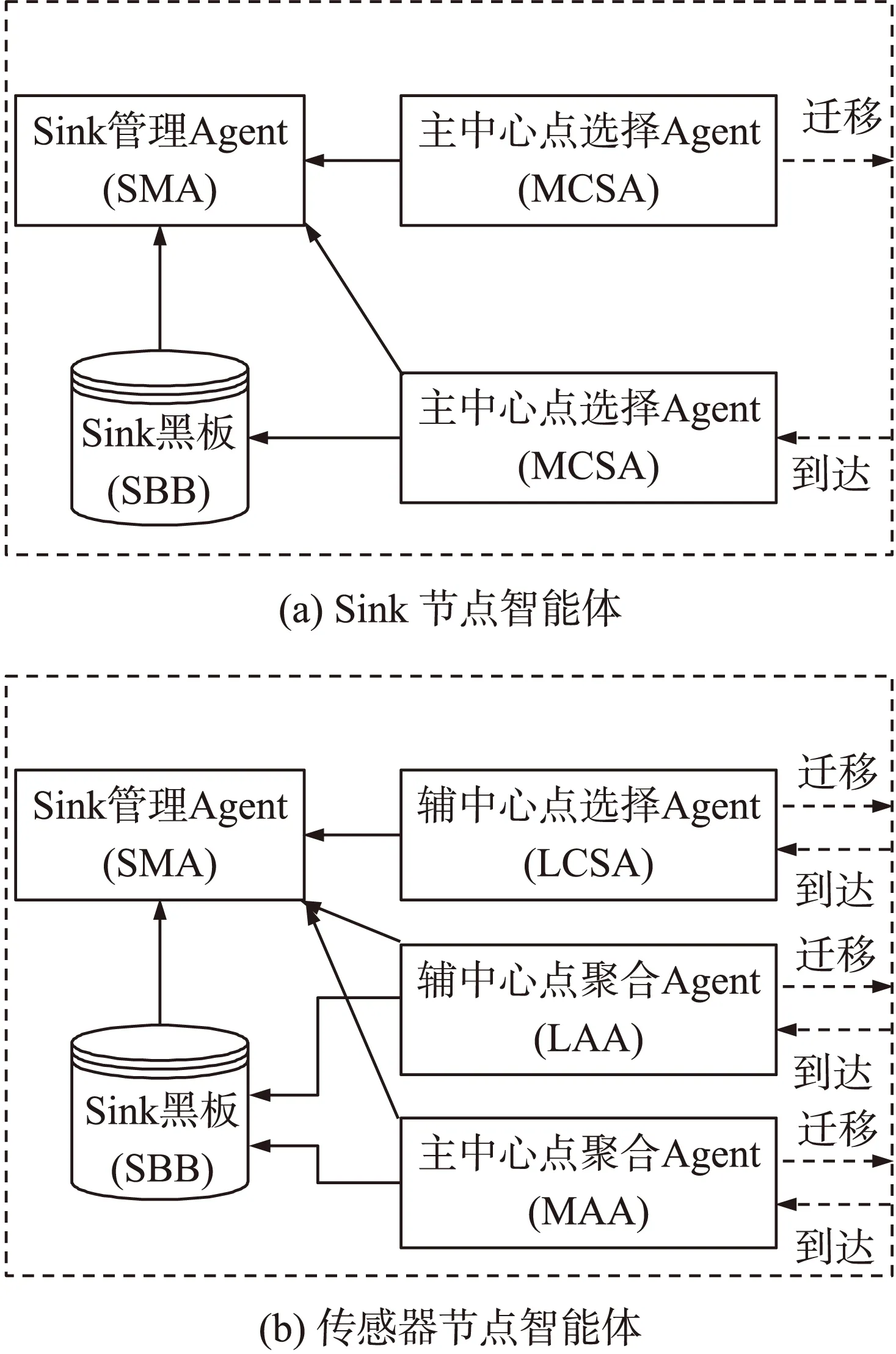
图2 多智能体结构

图2(b)为传感器节点Agent框架,主要组成部分有:

①节点管理Agent(NMA),为一静态的Agent,位于所有传感器节点中,它监测等数据信息、信号强度、传输距离、剩余能量等。并根据这些信息,控制节点开启或者关闭,从而对能耗进行控制。此外,NMA通过收集临近节点的ID、位置、权重系数等对NBB进行更新。

②局部辅中心点选择Agent(LASA),LASA由NMA触发,LASA从NBB中获取辅神经角度值,并把它发送到一跳距离的临近节点。

③辅中心点数据融合Agent(LAA),是由NMA驱动的移动Agent,获取局部路径信息以及NBB中的局部数据融合,并沿副神经移动到下一个局部中心点。LAA负责对每次局部中心的访问,都会持续将信息沿副神经传达到与其相连的主神经中心节点中。

④主中心点Agent(MAA),是由NMA驱动的移动Agent,获取主中心路径信息,并将与之相连的辅助神经融合数据沿主干神经传递到Sink节点中。五是节点黑板,定义同SBB类似。

2 主、辅中心选取

2.1 主中心节点选取

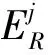
例如在选择S2作为主中心节点过程中,其上级节点为Sink节点S1,若S1坐标为(xi,yi),以S2为代表的S1邻域节点坐标为(xj,yj),则夹角θm(j)的计算公式为:

(1)

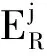
(2)

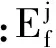
则S1邻域节点权重因子WM(j)计算公式为:

(3)

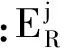
K=K1×A+K2×B

(4)

式中:A能量比,为节点的可用能量比。B邻域计数比,为通讯范围内活跃节点比例,A和B的最大取值为1。K1和K2为SMA的最小阈值常数,满足:

(5)

当θm(j)值增大,此时节点逐渐远离主中心节点,则WM值减小。通常选取θm(j)值较大的节点构建辅中心节点区域。

由SMA模块负责启动主中心点的选择过程,SMA给邻域节点发送查询信息,然后邻域节点的NMA负责计算权重WM,NMA将坐标和权重WM信息反馈到SMA,而后SMA计算欧式距离D[11～12]:

(6)

式中:i为Sink节点或上一级主中心节点,j为i邻域节点。然后SMA比较其所有邻域节点欧式距离D(i,j)与阈值Dmth,若D(i,j)>Dmth,则节点j作为MC节点选取的备选节点,对于所有的备选节点,选取权重WM最大的作为MC节点。若无邻域节点满足D(i,j)>Dmth,则降低阈值Dmth。算法伪代码如下:

Algorithm1:主中心点选取

1.Begini为选取的主中心节点;

2.令i为坐标原点,计算NC邻域点坐标(x2(j),y2(j));

3.计算所有节点的欧式距离D(i,j);

4.forj=1:NCdo

5.ifD(i,j)>Dmththen

6.ifx2(j)>x1(j)then

7.ify2(j)=y1(j)then

8.WM(j)=Wmin;

9.else

10.计算θm(j)和WM(j);

11.存储WM(j)到SBB中;

12.endif

13.endif

14.endif

15.endfor

16.选择最大WM(j)对应节点j作为主中心节点MC;

17.End

按照上述MC节点选取方法,SMA触发MCSA沿着主神经寻找其余MC节点,最后一个MC节点管理所有MC节点的ID信息。如图3(a)所示。图3(a)节点S12负责管理所有节点的ID信息,通过该信息可查询数据信号的传递路径,该图为一个最简单的无分叉的神经二部分裂结构的WSNs数据融合算法,S1为Sink节点,S2、S4、S5、S6、S8、S10、S11和S12为MC节点。

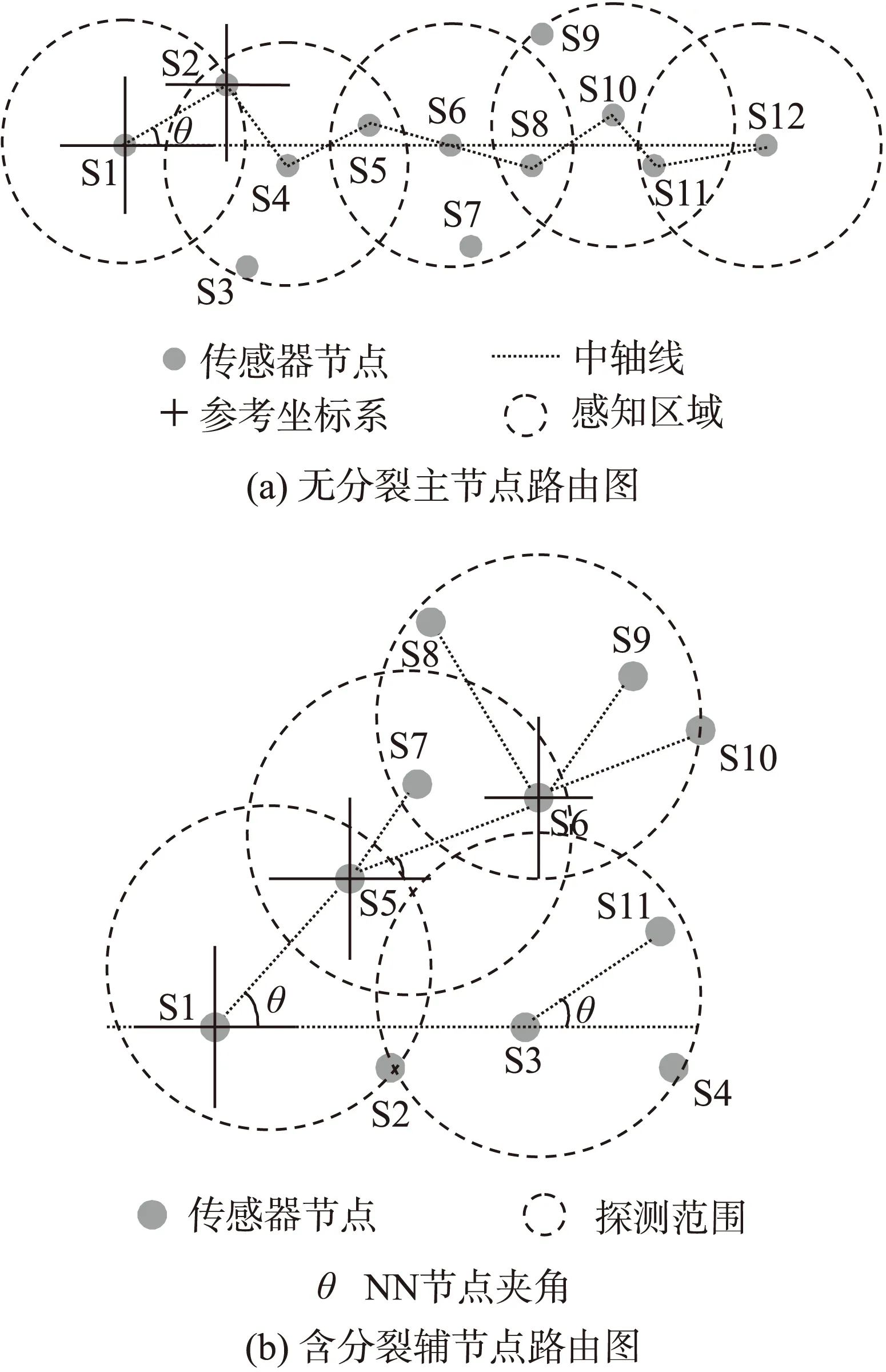
图3 主、辅中心节点选取

2.2 辅中心节点选取

理论上神经二部分裂结构的夹角变化范围为:0°～180°,但为保证该结构在WSNs区域内宽度和纵度延伸的均衡,设定角度取值范围为:

rib∈{135°～150°}∪{45°～60°}

(7)

此处,参数物理意义同主中心节点定义,不同的是,辅中心选取不必考虑夹角问题,则辅中心节点选取权重因子WL计算公式定义如下:

(8)

式中:K∈[0,1]为阈值常数。

邻域内节点满足式(7)所划定范围内,并且当阈值为Dlth时,满足D(i,j)>Dlth,则该节点将被作为辅中心节点(LC)。同MC选取方式类似,所有候选LC节点中,最大值WL所对应的节点,被选为LC节点。若无邻域节点满足D(i,j)>Dlth,则增大NMA或者降低阈值Dlth。当D(i,j)变化时,SMA负责管理阈值Dmth和Dlth,初始化SMA阈值参数R来存储MC和LC节点,变化规则为:①若中心节点已找到,则R→R+δ;②若中心节点未找到,则R→R+Iδ。

上述I=2p,p为整数。LC节点选取过程类似于MC节点的选取过程,如图3(b)所示。对于主中心节点S3,在LC节点S11选定后,由NMA触发LCSA沿着设定的角度取值范围rib,查找剩余LC节点,此处无其他LC节点,则节点S11亦作为最后一个LC节点负责存储信号传递路径信息。图中S1可作为Sink节点,LC节点S5、S6和S9直接与Sink节点相连,而S11则与2.1节确定的MC节点S3相连,信号通过S3中转传递到Sink节点。

3 数据融合及算法流程

3.1 LMS自适应加权融合

神经二部分裂结构的多智能体WSNs数据融合算法的数据融合涉及到3个层面:Part1:普通节点级融合;Part2:LC节点级融合;Part3:MC节点级融合。传统的无线传感器网络进行数据融合时需要节点的方差或观测方差,但在现实中信号的非平稳性,导致上述两个参量的统计特性很难得到[13～14],为提高融合精度此处采用LMS自适应加权融合。

定理1 对于图4递推系统,LMS自适应加权融合递推公式选取为:

(9)

时,系统收敛,当k→∞时,εk→0。

证明 假定k时刻传感器数量为N,则其加权系数可定义为:

(10)

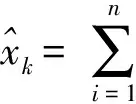
(11)

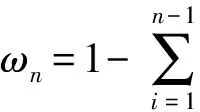
(12)

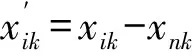
(13)

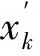
(14)

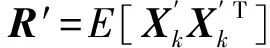
(15)

与之类似可定义:

(16)

则LMS自适应加权融合均方误差为:

(17)

则通过式(16)可看出,误差期望E(εk)为W′的二次型函数,为保证εk收敛,采用梯度下降法:

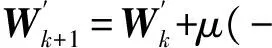
(18)

式中:μ为步长调整参数,k为加权梯度,其估计形式如下:

(19)

式(18)、式(19)结合可得LMS自适应加权融合递推公式:

(20)

证毕。

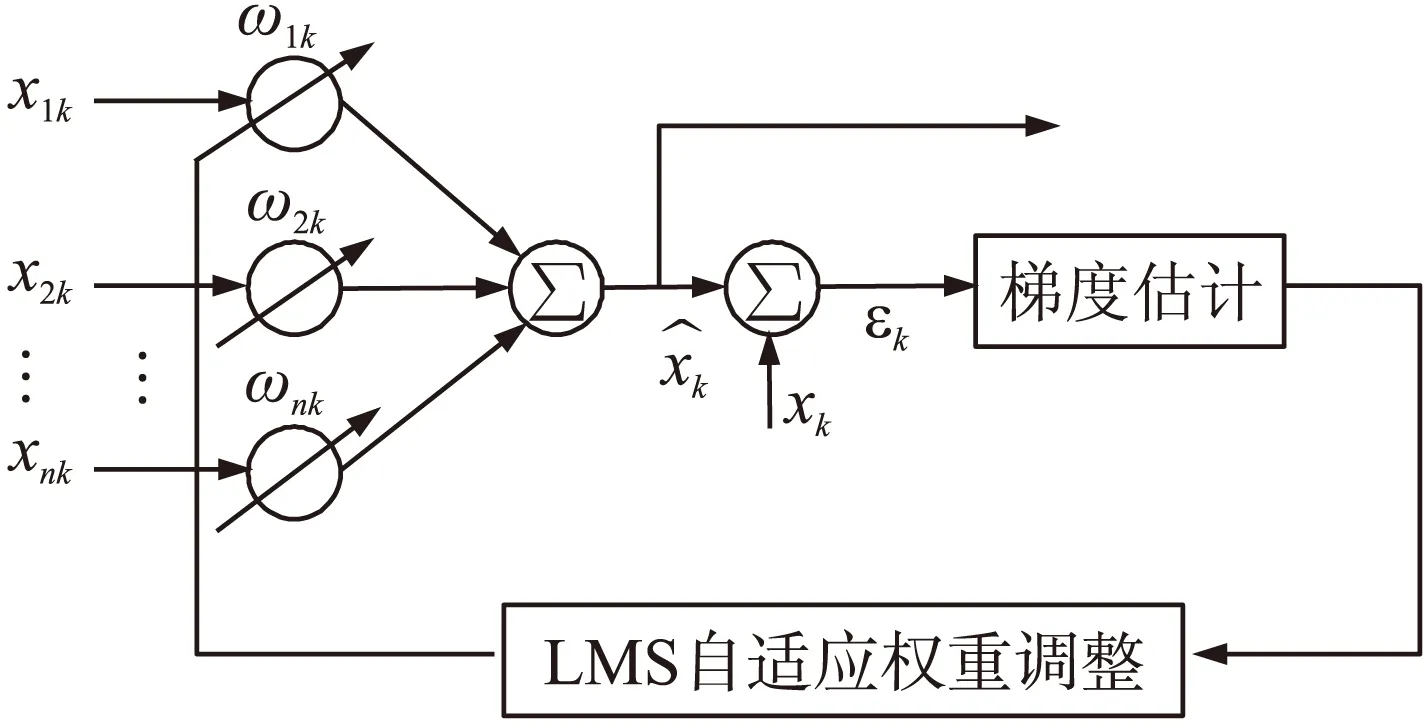
图4 递推算法

3.2 算法流程及时间复杂度分析

综上所述,在完整NBMA-WSNs算法中,应包含两个步骤:一是主辅节点选取;二是主辅节点数据融合。具体算法流程如图5所示。

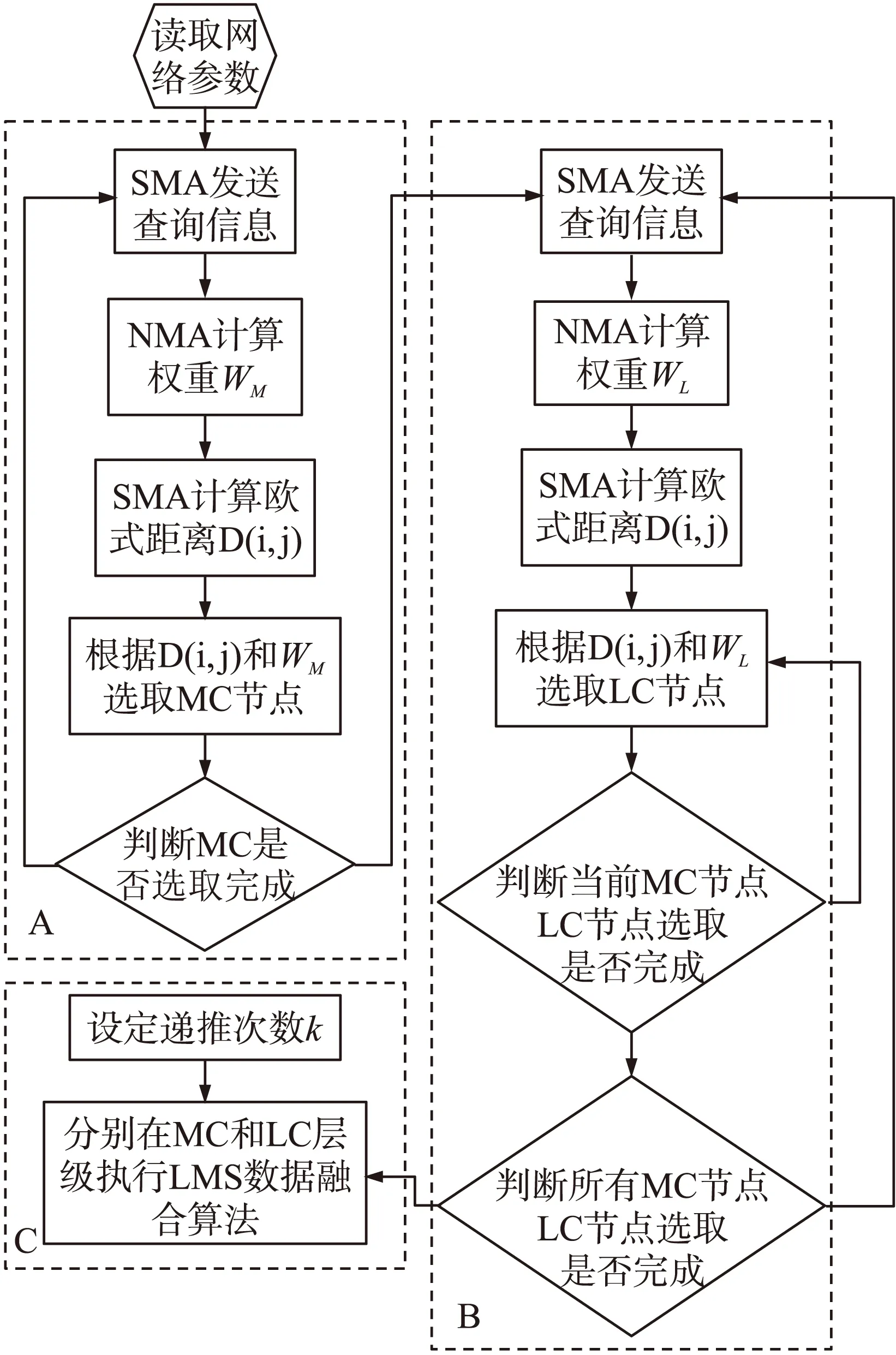
图5 算法流程

图5中,A为主中心节点选取过程,B为辅中心节点选取过程,C为数据融合过程。则根据上述算法流程,算法的时间复杂度可分析如下:令DAi={DAp1,DAp2,…,DApn}为在时间窗T=t1→tn={t1,t2,…,tn}内从节点i中采集的数据。令Docc为DAi中重复数据量,则重复比为:

PDocc=Docc/DAi

(21)

则融合数据超出DAi概率为:

PDagg=1-PDocc

(22)

令l为MC节点数量,则二部分裂结构下,连接到主神经的辅神经数量为:

Rntotal=2l

(23)

令TLp1,TLp2,…,TLpn为LC节点数据融合时间,则每个辅神经的融合时间为:

(24)

式中:αi<αi+1,α∈[0.001,0.003]。LC节点的总融合时间为:

TR=Rbagtime×Rntotal

(25)

令TM1,TM2,…,TMn为LC节点数据融合时间,则MC节点的总融合时间为:

(26)

式中:γi<γi+1,γ∈[0.003,0.005]。则总数据融合时间为:

Taggre=Magtime+TR

(27)

4 仿真实验与分析

实验平台:MATLAB R2012b,Intel i7 3.40 GHz处理器,4G RAM,Win7系统。实验区域大小为300 m×300 m,共由500个传感器节点。当节点能量降为0时,宣布该节点“失效”。仿真参数设置如表1所示。

表1 仿真参数

为验证NBMA-WSNs算法的有效性,选取仿真对比指标:失效CHs,Sink节点接收数据包数量,能量消耗和标准偏差。对比算法选取WSNs分布式能量均衡算法(DEBR)[15]和WSNs轮盘触发数据融合算法(WBTDA)[7]算法。DEBR方法和WBTDA方法均是从各节点能耗均衡角度出发,提高网络寿命,但过分考虑能耗,牺牲部分数据传输效率,实际中可对耗能较大的节点,提高其电池储量方式,提高节点利用效率。如本文中选取的主辅节点可通过增配电池容量方式,实现网络寿命延长的同时,不降低数据传输效率。假定Sink节点位于区域中间位置,则MC和LC节点的选取如图6所示,性能对比如图7(a)～7(d)所示。

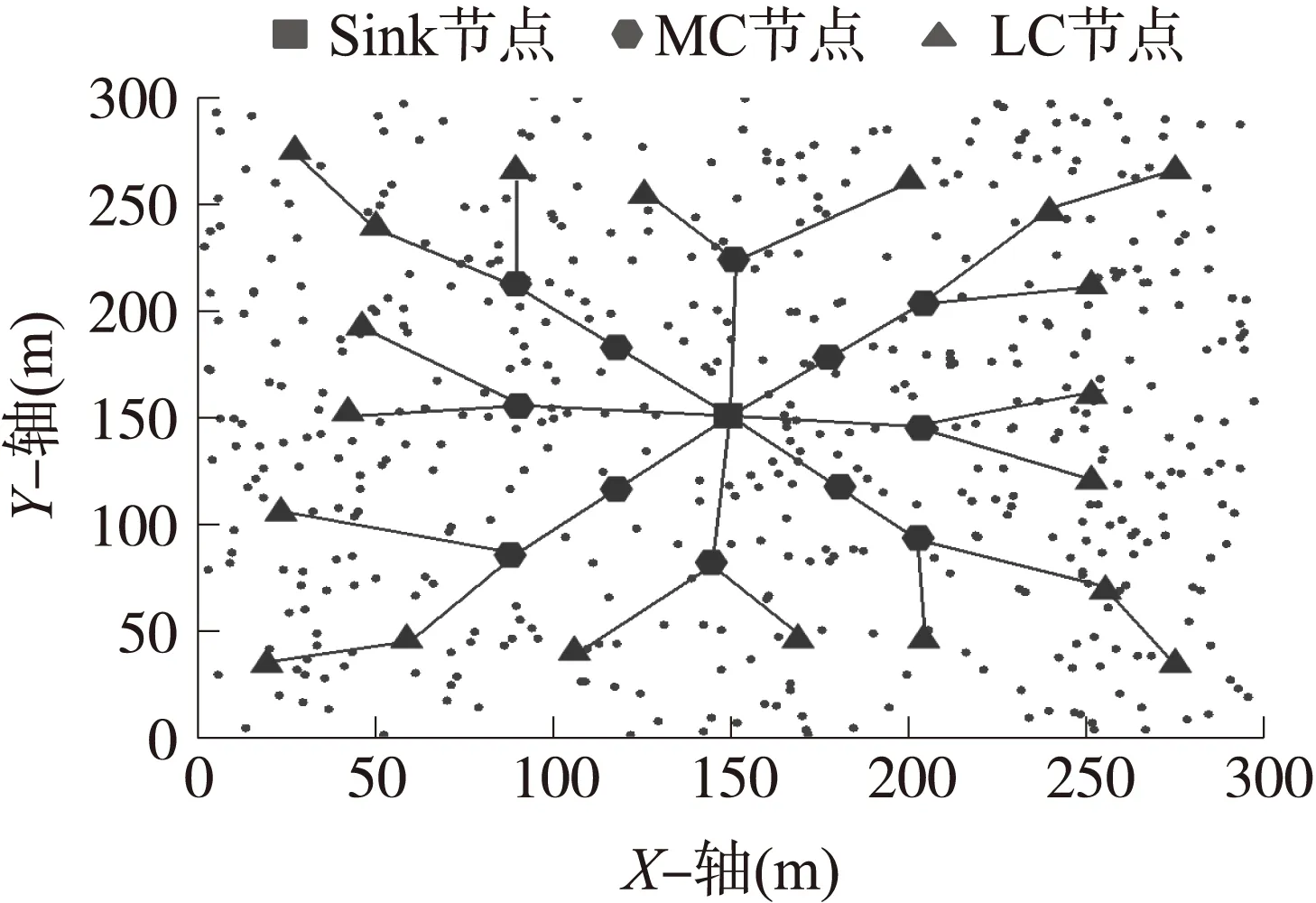
图6 二部神经网络结构

图6给出了上述实验环境下的神经二部分裂结构图,其中,黑三角为LC节点,黑六边形为MC节点,黑四边形为Sink节点,上述节点共有33个,LC节点位于区域边缘与Sink节点直接通讯的能耗较大,为此MC节点作为中继负责联系LC节点与Sink节点的通讯。Sink节点赋予较大能量值,MC节点能量较高,LC节点能量次之,普通传感器节点的能量配备最低,通过此方式可有效降低组网成本,平衡能量分布和消耗,同时还起到节省能耗的作用,延长网络使用寿命。

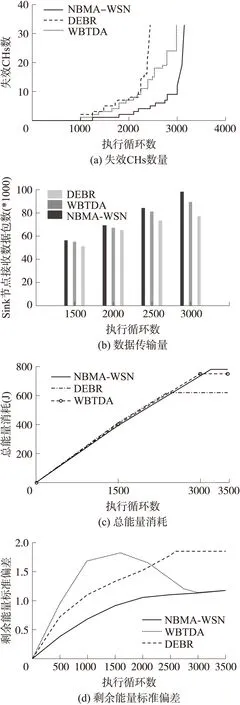
图7 算法性能对比

图7(a)给出随着执行循环数的增加,失效CHs数量的变化情况,CHs失效意味着能量的耗尽,从图中可以看出,NBMA-WSNs算法在该指标上要明显好于DEBR和WBTDA算法。其中DEBR算法最早能量耗尽,网络的生存周期最短。主要原因在于,DEBR算法采取的分布式直连方式,存在数据传输距离过长,能耗过多的问题。而WBTDA算法为平衡能量消耗,执行的策略是数据包可能会通过其他的CHs穿往Sink节点,但是问题是如果选择了相反的方向,会导致数据包无法到达Sink节点处,虽然平衡了能量,但同时也浪费了能量。相比而言,NBMA-WSNs算法在处理能耗节省和平衡上具有优势。图7(b)给出随着执行循环数的增加,Sink节点接收到的总数据包数量情况。从接收数据总量看,NBMA-WSNs算法要多于对比算法,并且随着执行循环数增加,存在能量耗尽,CHs失效的情况,导致NBMA-WSNs算法与对比算法在接收数据量的差距越来越大。图7(c)给出随着执行循环数的增加,传感器网络的总能耗,虽然各网络初期能量的消耗率差不多,但是由于NBMA-WSNs算法网络中处于活跃状态的节点要多于DEBR和WBTDA算法,所以在传输更多数据量的同时,消耗相对较多的总能量。图7(d)给出随着执行循环数的增加,剩余能量标准偏差,该指标主要反映能耗平衡情况。从图7(d)中可看出,NBMA-WSNs算法的剩余能量偏差始终处于较低的水平,说明节点的剩余能耗相差不多,从而反映出节点能耗的平衡。

5 结束语

从降低和平衡能耗角度,借鉴神经结构的主干、分支信息传递方式,设计一种神经二部分裂结构的多智能体WSNs数据融合路由算法。给出了主干、分支路径中,主辅节点的选取算法,并且提出一种基于LMS的自适应加权融合算法,实现数据从普通节点到LC节点到MC节点到Sink节点的数据融合算法,仿真结果验证了所提算法的有效性。本文算法的不足是,由于主辅节点选取特点,其承载的数据传输量会增大,为保持能耗剩余均衡,需对这样节点电量进行增配,因此网络部署前期工作相对繁琐一些。

[1] 程红举,黄行波. 不可靠通信环境下无线传感器网络最小能耗广播算法[J]. 软件学报,2014,25(5):1101-1112.

[2] Zhang Y Z,Zhang X H,Fu W Y. HDRE:Coverage Hole Detection with Residual Energy in Wireless Sensor Networks[J]. Journal of Communications and Networks,2014,16(5):1229-2370.

[3] Hua C Q,Yum T S. Data Aggregated Maximum Lifetime Routing for Wireless Sensor Networks[J]. Ad Hoc Networks,2008,6(3):380-392.

[4] Huifang C,Hiroshi M,Tadanori M. Adaptive Data Fusion Scheme in Clustered Wireless Sensor Networks[J]. Computer Communications,2008,35(15):3579-3585.

[5] 王涛春,秦小麟,刘亮. 无线传感器网络中安全高效的空间数据聚集算法[J]. 软件学报,2014,25(8):1671-1684.

[6] 张品,董为浩,高大冬. 一种优化的贝叶斯估计多传感器数据融合方法[J]. 传感技术学报,2014,27(5):643-648.

[7] Sutagundar A V,Manvi S S. Wheel Based Event Triggered Data Fusion and Routing in Wireless Sensor Networks:Agent Based Approach[J]. Wireless Pers Commun,2013,71(2):491-517.

[8] 杨雅辉,黄海珍,沈晴霓. 基于增量式GHSOM神经网络模型的入侵检测研究[J]. 计算机学报,2014,37(5):1216-1223.

[9] Kuila P,Jana P K. Approximation Schemes for Load Balanced Clustering in Wireless Sensor Networks[J]. Journal of Supercomputing,2014,68(1):87-105.

[10] 刘端阳,暴占兵,程珍. 一种可分负载WSNs的能耗均衡负载调度算法[J]. 传感技术学报,2014,27(2):225-232.

[11] Yuan F,Zhan Y J,Wang Y H. Data Density Correlation Degree Clustering Method for Data Fusion in WSNs[J]. IEEE Sensors Journal,2014,14(4):1089-1098.

[12] Tseng F H,Cho H H,Chou L D. Efficient Power Conservation Mechanism in Spline Function Defined WSNs Terrain[J]. IEEE Sensors Journal,2014,14(3):853-864.

[13] Demigha O,Hidouci W K,Ahmed T. On Energy Efficiency in Collaborative Target Tracking in Wireless Sensor Network:A Review[J]. IEEE Communications Surveys and Tutorials,2013,15(3):1210-1222.

[14] 李建洲,王海涛,陶安. 一种能耗均衡的WSNs分簇路由协议[J]. 传感技术学报,2013,26(3):396-401.

[15] Ok C S,Lee S,Mitra M. Distributed Energy Balanced Routing for Wireless Sensor Networks[J]. Computer and Industrial Engineering,2009,57(1):125-135.

屠雄刚(1977-),男,硕士,浙江师范大学,数理与信息工程学院副教授,研究方向为模式识别智能计算等,tuxiongg@sina.cn;

陈 军(1980-),女,硕士,浙江工业职业技术学院设计与艺术学院副教授,研究方向为图像处理,模式识别;

张长江(1974-),男,博士,浙江师范大学数理与信息工程学院教授,研究方向为图像处理,模式识别,机器学习,多尺度几何分析及应用。

NBMA-WSNs:Neural Bipartitions Structure Based MultiagentWSNs Fusion Algorithm*

TUXionggang1,2*,CHENJun2,ZHANGChangjiang1

(1.College of Mathematics Physics and Information Engineering,Zhejiang Normal University,Jinhua Zhejiang 321004,China;2.School of Design and Arts,Zhejiang Industry Polytehnic College,Shaoxing Zhejiang 312000,China)

In order to further improve the wireless sensor network(WSNS)service life,from the angle of improving the efficiency of data fusion algorithm,,a neural bipartitions structure based multi-agent WSNs fusion algorithm was proposed. Firstly,according to the trunk and branches of the nerve structure bearing different amount of information,the trunk and branches were selected to construst the communication link,then the main,auxiliary center node’s selection method was also used. Secondly,the adaptive weighted fusion algorithm based on LMS was designed,which processed the node,the branches and the trunk center level to realize the aggregative for the neural bipartitions structure. Finally,through simulation compared with two existing algorithms,this algorithm shows the advantages at the indicators such as the Sink node’ss packet reception,the energy consumption,and so on,which verified the effectiveness of the algorithm.

wireless sensor network;multi-agent;neural bipartitions;fusion

项目来源:国家自然科学基金项目(61202029,61272449);浙江省自然科学基金项目(LY12E05016)

2014-12-28 修改日期:2015-02-16

C:6150P

10.3969/j.issn.1004-1699.2015.06.022

TP393.09

A

1004-1699(2015)06-0907-07