基于Lévy飞行特征的蝙蝠算法及其在WSN定位中的应用*

石 浩,王万良,李燕君,卢良进

(浙江工业大学计算机科学与技术学院,杭州 310023)



基于Lévy飞行特征的蝙蝠算法及其在WSN定位中的应用*

石 浩,王万良*,李燕君,卢良进

(浙江工业大学计算机科学与技术学院,杭州 310023)

针对蝙蝠算法收敛易早熟、收敛速度慢等不足,提出一种改进的基于Lévy飞行特征自适应的蝙蝠算法。采用Lévy飞行策略取代原算法中蝙蝠飞行速度和位置的更新方式,充分利用Lévy飞行的重尾效应,有效避免局部最优值的吸引,加快了收敛速度,达到寻优能力和搜索能力的平衡。在无线传感器网络自身定位应用中,把定位问题转换为一个全局优化问题,使用改进的算法进行定位计算。通过Zigbee平台的实验表明,改进后的算法在不同空间位置的定位精度更高,收敛速度更快。算法实现条件简单、精度高,具有较高的实际工程应用价值。

无线传感器网络;RSSI;定位算法;蝙蝠算法;Lévy飞行

无线传感器网络WSN(Wireless Sensor Networks)是由分布在监控区域内的许多廉价传感器节点组成,采用无线通信的方式组成的一个多跳自组织的网络系统,具备监测、感知、采集和处理等功能[1]。近年来,WSN作为物联网产业的核心技术日益受到研究者的重视,在室内导航、火灾定位、安保系统和健康监护等应用中有着研究。在一些实际应用中,节点的位置都是随机并且未知的,节点所采集到的数据必须结合其位置信息才有意义。因此,实现节点的自身定位对无线传感器网络具有重要意义。

WSN的定位技术分为两类算法:测距的定位算法(Range-based)和无需测距的定位算法(Range-free)[2]。测距的定位算法通过使用复杂的硬件设备获取节点之间的距离和角度,来计算定位信息,如TOA(到达时间法)、TDOA(到达时间差)、AOA(达到的角度),RSSI(信号强度指示值)算法等;无需测距的定位算法是利用WSN的网络连通性来计算距离,虽然不能精确得到节点间准确的距离,但是由于使用的设备简单、成本低,使此类算法有着广泛的应用[3],如质心定位、DV-Hop[4]、APIT[5]、MDS-MAP[6]等算法。文献[7]提出在煤矿井下应用中使用改进的RSSI指纹定位匹配算法,使用K邻近算法和最短历史路径匹配法,利用机车速度对定位算法精度进行修正。文献[8]提出改进的DV-Hop定位算法,使用自适应蜂群算法计算未知节点坐标,提高了定位精度和精度稳定性。文献[9]比较了遗传算法和人工蜂群算法在WSN中的应用,得出人工蜂群算法在WSN定位中可以得到比遗传算法更佳的精度。文献[10]提出改进的蝙蝠算法,通过调整声音响度和脉冲发射频率来提高寻优性能。由于蝙蝠算法的局部搜索性能优于全局搜索性能[11],这个算法只改进了蝙蝠算法的局部搜索性能,对全局搜索性能没有改进。文献[12]提出了具有Lévy飞行特征的蝙蝠算法,修改了蝙蝠个体位置更新的公式,使用Lévy飞行特征产生蝙蝠个体的新位置,改进了蝙蝠算法的全局搜索性能。由于在最优解附近通过Lévy飞行产生的新解,会与局部最优解相距较远,反复的搜索运算降低了算法的效率。本文在基本的蝙蝠算法上使用Lévy飞行随机游走的特性拓展了搜索的空间,加快了算法的收敛速度,提出蝙蝠个体基于Lévy飞行自适应的位置更新方法,提高了蝙蝠算法的全局搜索性能,使全局搜索能力和局部搜索能力达到平衡。

1 WSN定位算法模型

1.1 基于RSSI的WSN测距模型

无线电波的发射功率具有随着距离增加而衰减的特性,无线电波在自由空间中传播,自由空间传播模型为[13]:

(1)

式中:Pr为信号接收功率,Pt为信号发送功率,Gt为发射天线增益,Gr为接收天线增益,λ为波长,d为发射端和接收端之间的距离。式(1)表明随着发射距离的增加,接收功率指数倍下降。无线电波的自由空间传播模型的对数模型为:

Pl(d)=Pl(d0)-10×n×log(d/d0)+Xp

(2)

式中:Pl(d)为距离为d时信号的接收功率;d0为参考距离,一般为1m;Xp为平均值为零的高斯分布随机变量。n为路径损耗指数,不同环境和不同天线有不同的值,通常在2到4之间。在实际应用中,为了达到较好的测距精度,需要测量环境中的路径损耗指数。

1.2 基于RSSI的定位算法模型

假设在自由空间区域,信标节点A、B、C、D和未知节点N组成无线传感器网络,如图1所示。

图1 信标节点和未知节点的示意图

图1中:信标节点A、B、C、D的坐标分别为(xA,yA)、(xB,yB)、(xC,yC)和(xD,yD);信标节点A、B、C、D和未知节点N(x,y)的距离分别为:dA、dB、dC、dD。文献[8]和文献[9]通过遗传算法和蜂群算法的将定位问题转换为全局优化问题,求的未知节点N的坐标,文献中使用的适应度函数为:

(3)

式中:(x,y)为未知节点坐标;(xi,yi)为信标节点坐标;n表示信标节点数量;di是根据无线电波与距离衰减模型映射的距离;求得的最小值minf(x,y)即为最优解。

在实际环境中,信号接收端接收的信号强度(RSS)和距离的并不是线性关系,某实际环境中RSS和距离的曲线如图2所示。

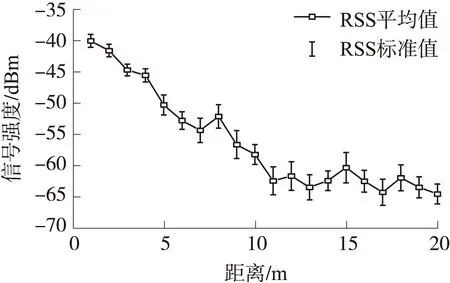
图2 实际环境中RSS与传输距离的曲线

图2中,信标节点和未知节点距离小时,曲线线性好;距离大时,曲线线性差,并且标准差也较大。说明:节点距离越大,对定位精度的影响越大。在式(3)中,没有考虑不同节点距离对定位精度的影响。为了提高适应度函数的准确性,在适应度函数中增加距离的倒数作为权重系数,如式(4)所示。

(4)

2 基于Lévy飞行特征的蝙蝠算法

2.1 蝙蝠算法描述

近年来,具有自然进化思想的元启发式算法(Meta-heuristicAlgorithms)掀起了国内外科学家研究的热潮。元启发式算法的思想是人们在长期的生产实践中,对物理、生物、社会等现象经过长期观察和深入研究,模拟自然现象的运行机制得到的知识结晶。新型元启发式算法例如蚁群优化算法、萤火虫算法、布谷鸟搜索算法、和声搜索算法已经成为现今复杂的优化问题的有效解决方法。

蝙蝠算法[14]BA(BatAlgorithm)是由剑桥大学的Xin-SheYang在2010年提出的一种新的元启发式优化算法。蝙蝠算法是模拟蝙蝠回声定位行为,采用不同的脉冲发射频率和响度,通过全局搜索的办法找到最优解。蝙蝠算法已经逐渐在各个应用领域中受到学者的重视,针对蝙蝠算法全局搜索能力不佳的缺点,有许多文献展开研究。文献[15]提出了使用蝙蝠算法优化电力系统稳定性的问题(PSS)。文献[16]提出在蝙蝠算法中使用模拟退火和的高斯扰动算法,对蝙蝠个体进行高斯扰动,增加了全局搜索性能。

2.2 改进的Lévy飞行特征的蝙蝠算法

Lévy飞行的数学模型是由法国数学家PaulLévy提出,它是一种马尔可夫过程,行走的步长满足重尾(Heavy-tailed)分布[17],步长μ和出现的频率P(μ)的公式为:

P(μ)=μ-λ, 1<λ<3

(5)

Viswanathan经过研究发现,Lévy飞行现象在自然界很普遍,如蚂蚁或果蝇等动物搜索食物的行走路径[18],甚至是人在户外的某些活动路径也服从Lévy分布[19]。在大范围的搜索的过程中,Lévy飞行比布朗随机运动更佳有效[20],Lévy飞行在搜索过程中会产生较大跳跃,并且方向会急剧变化,这样可以使智能算法跳出局部最优。特别在高维复杂空间中,通过Lévy飞行扩大搜索空间,能够有效提高算法的收敛速度。Lévy飞行1000步的二维轨迹如图3所示,图中“○”表示起点,“☆”表示终点。

图3 Lévy飞行轨迹

基于Lévy飞行特征的蝙蝠算法的主要计算过程如下:

步骤1:定义适应度函数f(x),x=(x1,x2,…,xd)T,其中d为维数,x为蝙蝠个体的位置,f(x)的最优解就是蝙蝠个体找到猎物的位置;

步骤2:初始化蝙蝠种群位置xi(i=1,2,3,…,n)(n为种群数量)和飞行速度vi;

步骤3:定义蝙蝠个体在位置xi的频率fi;

步骤4:定义蝙蝠发出的音量Ai、脉冲发生率ri、迭代次数。通常为了简易计算,音量和脉冲发生率都设为常数0.5;

步骤5:通过调整频率产生新的新的位置(新解),并且更新位置xi和速度vi。

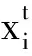
fi=fmin+(fmax-fmin)β

(6)

式中:fmax和fmin是声音频率的最大和最小值;β∈[0,1]是一个服从均匀分布的随机向量。

vt=vt-1+(xt-1-x*)f

(7)

式中:x*表示当前全局最优解,它是在所有n只蝙蝠搜索到的解中进行比较而得到的位置。

xt=xt-1+vt

(8)

式(8)表示蝙蝠个体更新之后的位置。

一个优秀的智能算法,需要达到全局搜索性能和局部搜索性能的平衡,这样既能避免收敛早熟,又有较佳的寻优性能[21]。传统的蝙蝠算法,式(6)中β是服从均匀分布,蝙蝠个体根据布朗运动更新位置。Lévy飞行的优点在于:使用Lévy分布比使用高斯分布或者泊松分布更不易访问到前一次的位置[22]。使用Lévy飞行策略更新蝙蝠飞行的位置,会扩大蝙蝠个体的搜索空间,提升蝙蝠算法在高维空间的寻优能力,避免蝙蝠个体陷入局部最优。文献[12]提出的基于Lévy飞行的蝙蝠算法,把速度和位置更新式(7)和式(8)改为:

xt=xt-1+Lévy(λ)⊗(xt-1-x*)

(9)

考虑到随着迭代次数的增加,蝙蝠个体会越来越接近全局最优解,相应地逐步减小Lévy飞行的搜索步长,会加快算法收敛速度,改进的算法为:

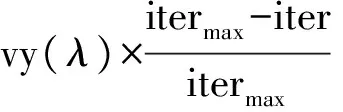
(10)

步骤6:根据音量Ai和脉冲发生率ri,判断局部最优解;

在每次迭代的过程中,音量Ai和脉冲发生率ri的更新公式为:

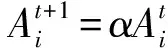
(11)

(12)

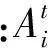
(13)

根据Ai和ri选择局部最优解的伪代码如表1所示。

表1 最优解判断伪代码

从最优解集中选择一个解,在选择的最优解周围产生一个新解,公式为:

xnew=xold+εAt

(14)

式中:ε∈[-1,1]是一个服从均匀分布的随机数;At是所有蝙蝠在同一个时间段的平均音量;xold是当前全局最优解;xnew是根据当前全局最优解产生的新解。

步骤7:排列适应度函数的数值,更新最优解集;

步骤8:循环次数递增,重复步骤5～步骤7;

步骤9:满足终止条件,达到最大迭代次数。

3 实验和性能分析

3.1 实验环境设置

在实际环境中进行实验,验证算法的准确性。实验场地为一个10 m×10 m的室内平面楼层,信标节点分别放置在:A(0,0)、B(10,0)、C(0,10)和D(10,10),如图4所示。

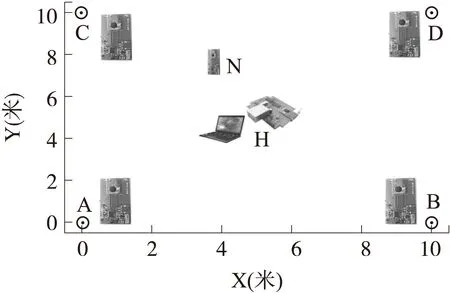
图4 实验场地示意图

未知节点N在定位区域中,向4个信标节点A、B、C和D广播信号,4个信标节点收到未知节点的定位信号之后,读出信号强度RSS并发送给信号集中器H。信号集中器通过USB传输线与PC机相连,将所有的定位信息以串行传输的方式传送给PC。在PC机上使用定位算法进行计算,得到未知节点N的坐标。

3.2 实验系统硬件

无线传感器节点采用作者自己制作的设备,分为传感器节点和信号集中器,如图5所示。传感器节点既作为信标节点又作为未知节点。信号集中器负责采集数据并上传PC机。设备单片机采用的是德州仪器的(TI)MSP430G2452十六位微处理器,RF采用的是TI CC2500低功耗2.5 G全双工射频芯片。CC2500发射功率最大为0 dBm(1 mW),在2.4 K的接收速率下,接收端灵敏度为-108 dBm。节点设备通讯范围为可达到50 m,非常适合构建无线传感器网络。实验中使用计算机CPU配置为Intel Core i5,主频为2.67 GHz,内存为4 GB。

图5 传感器节点设备

3.3 平均定位误差

平均定位误差是评估系统定位性能的指标之一,节点的实际位置和估算位置之间的误差由下面的关系式计算:

(15)

式中:(xest,yest)为估算节点坐标,(xr,yr)为实际节点。

根据WSN中所有的定位结果,定义平均定位误差:

(16)

式中:(xr,yr)为实际节点坐标,(xi,yi)为不同计算次数的估算坐标,n为计算次数。

3.4 实验结果和分析

在实验中,把未知节点放置在平面测量区域中不同的位置(中心、左下角、右上角),使用蝙蝠算法(BA)、文献[12]提出的基于Lévy飞行的蝙蝠算法(LBA)和本文提出的改进的Lévy飞行特性的蝙蝠算法(MLBA)3种算法比较节点在不同位置的定位性能。在不同的位置,分别使用3种算法运行100次,记录定位误差。蝙蝠算法初始化参数,如表2所示。

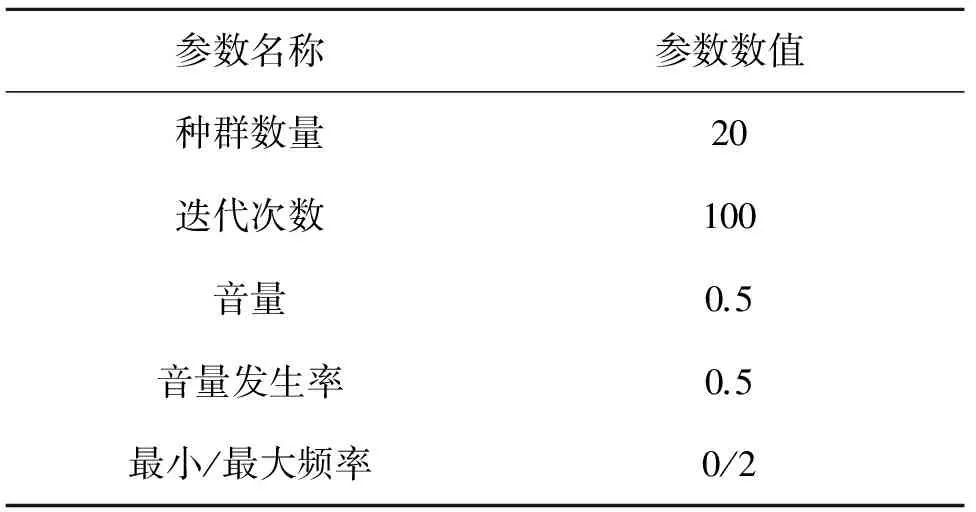
表2 蝙蝠算法参数

未知节点在中心,坐标为(5,5),使用BA、LBA和MLBA算法得到的实验结果如图6～图8所示,纵坐标表示定位误差,横坐标表示未知节点的计算的次数。未知节点在左下角,坐标为(2,2),分别使用3种算法得到的实验结果如图9～图11所示。未知节点在右上角,坐标为(8,8),分别使用3种算法得到的实验结果如图12～图14所示。

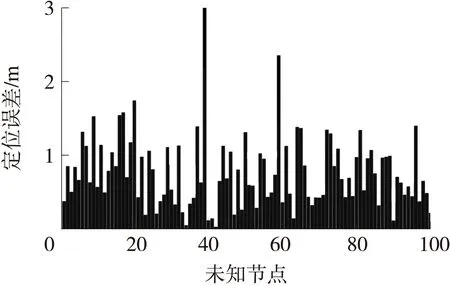
图6 BA算法定位中心节点的结果

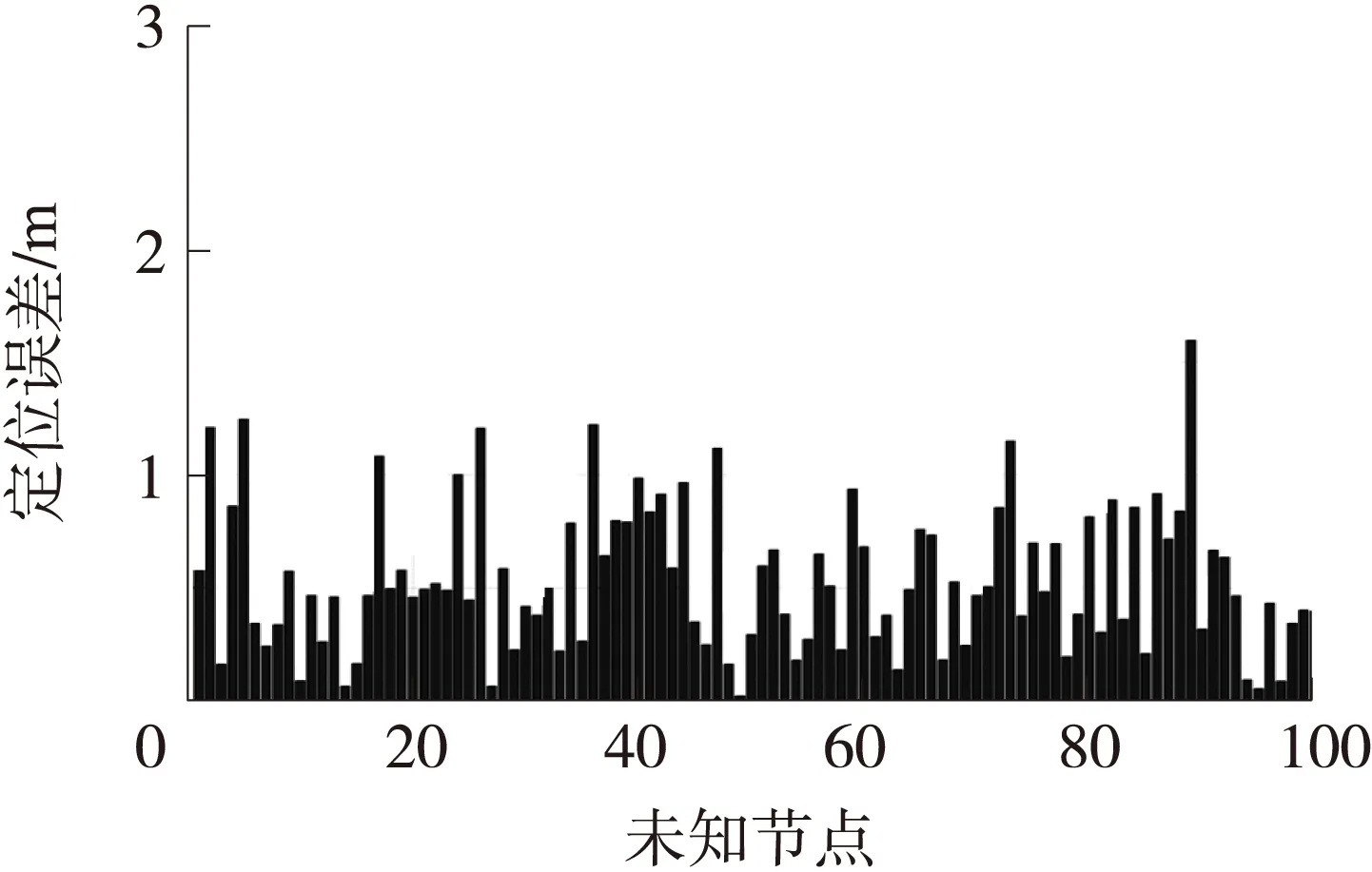
图7 LBA算法定位中心的节点的结果

图8 MLBA算法定位中心节点的结果

图9 BA算法定位左下角节点的结果

图10 LBA算法定位左下角节点的结果

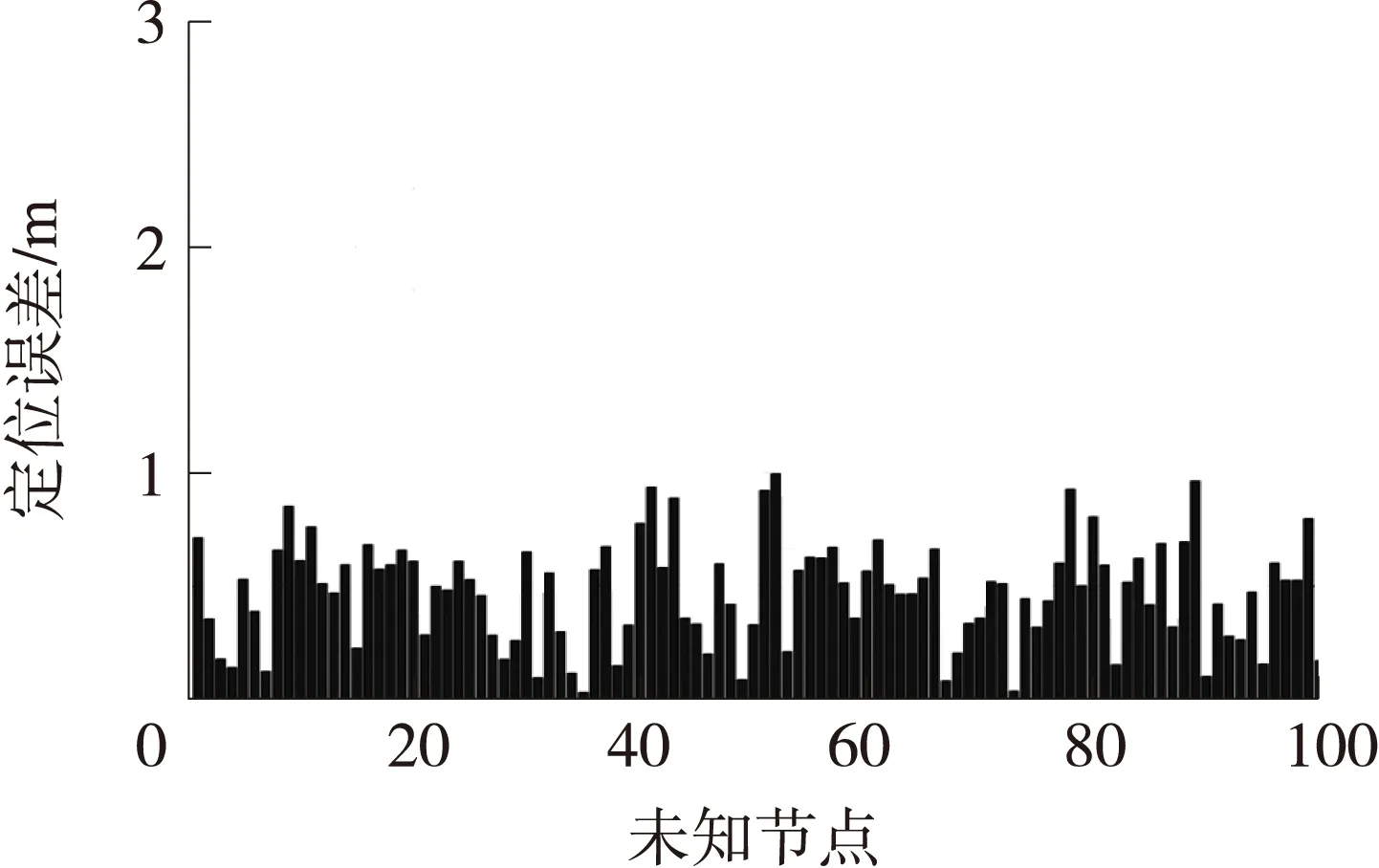
图11 MLBA算法定位左下角节点的结果

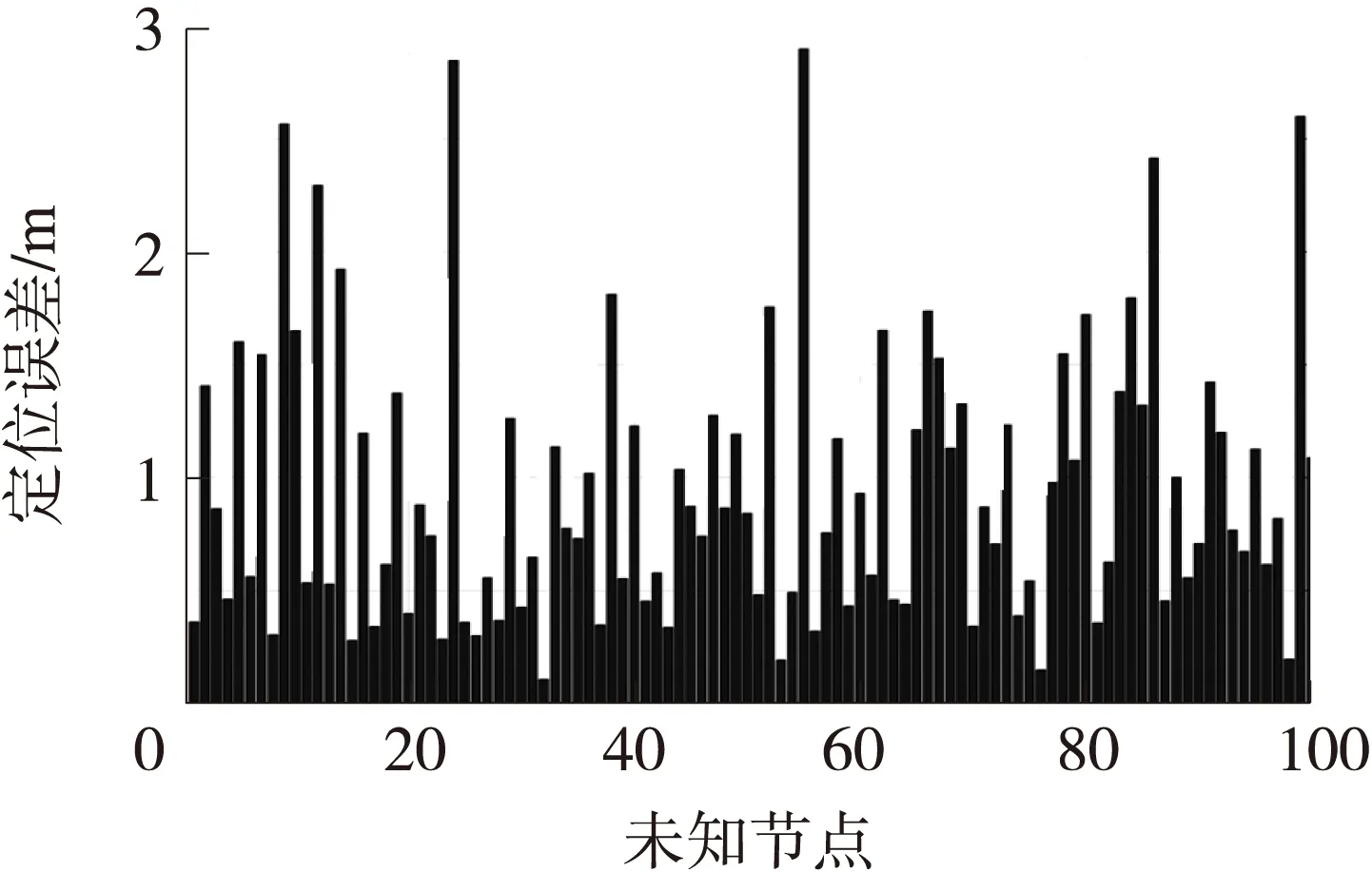
图12 BA算法定位右上角节点的结果

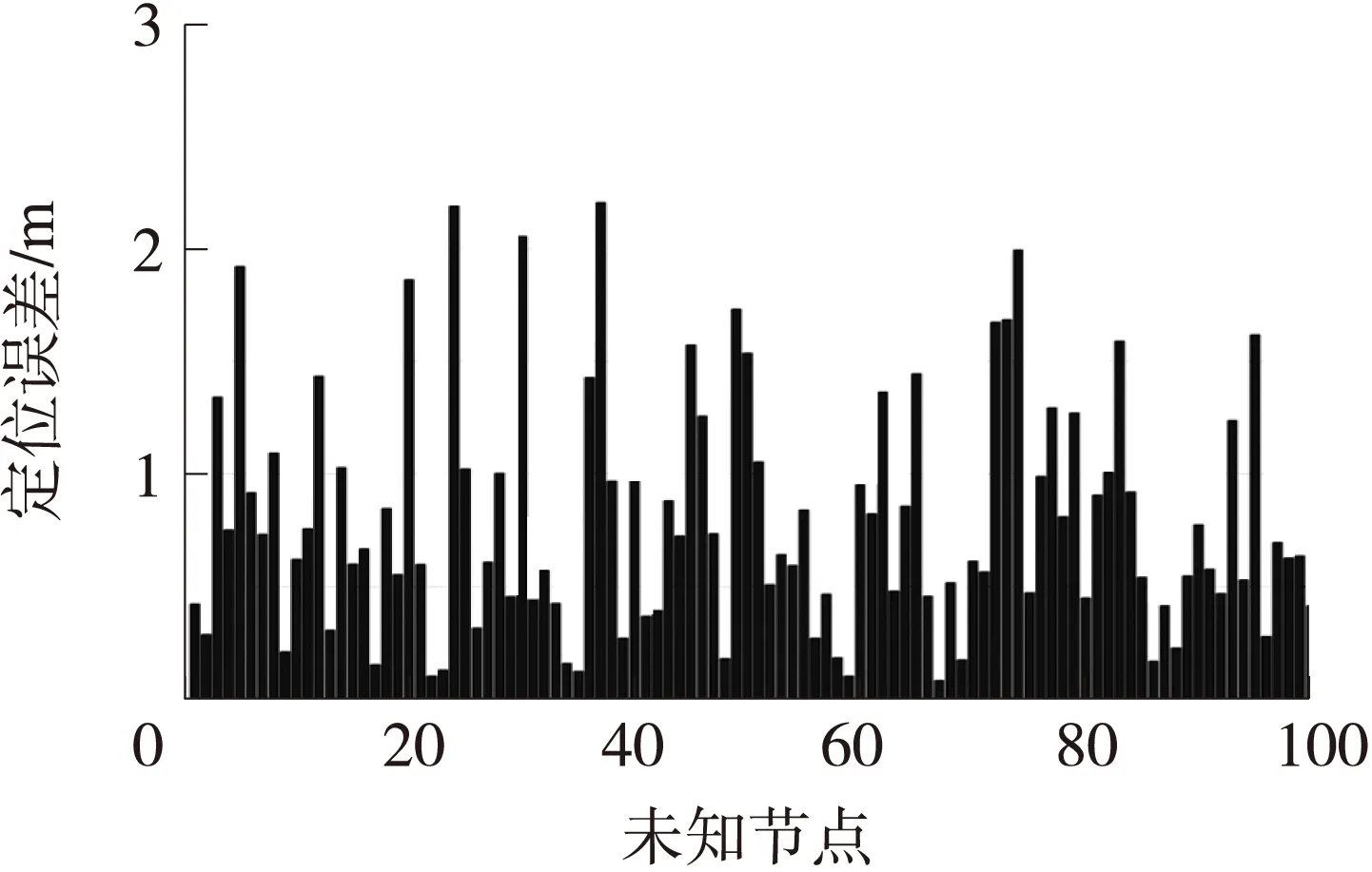
图13 LBA算法定位右上角节点的结果

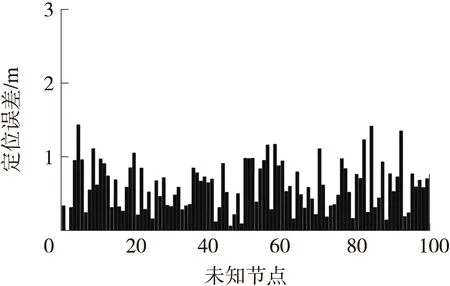
图14 MLBA算法定位右上角节点的结果

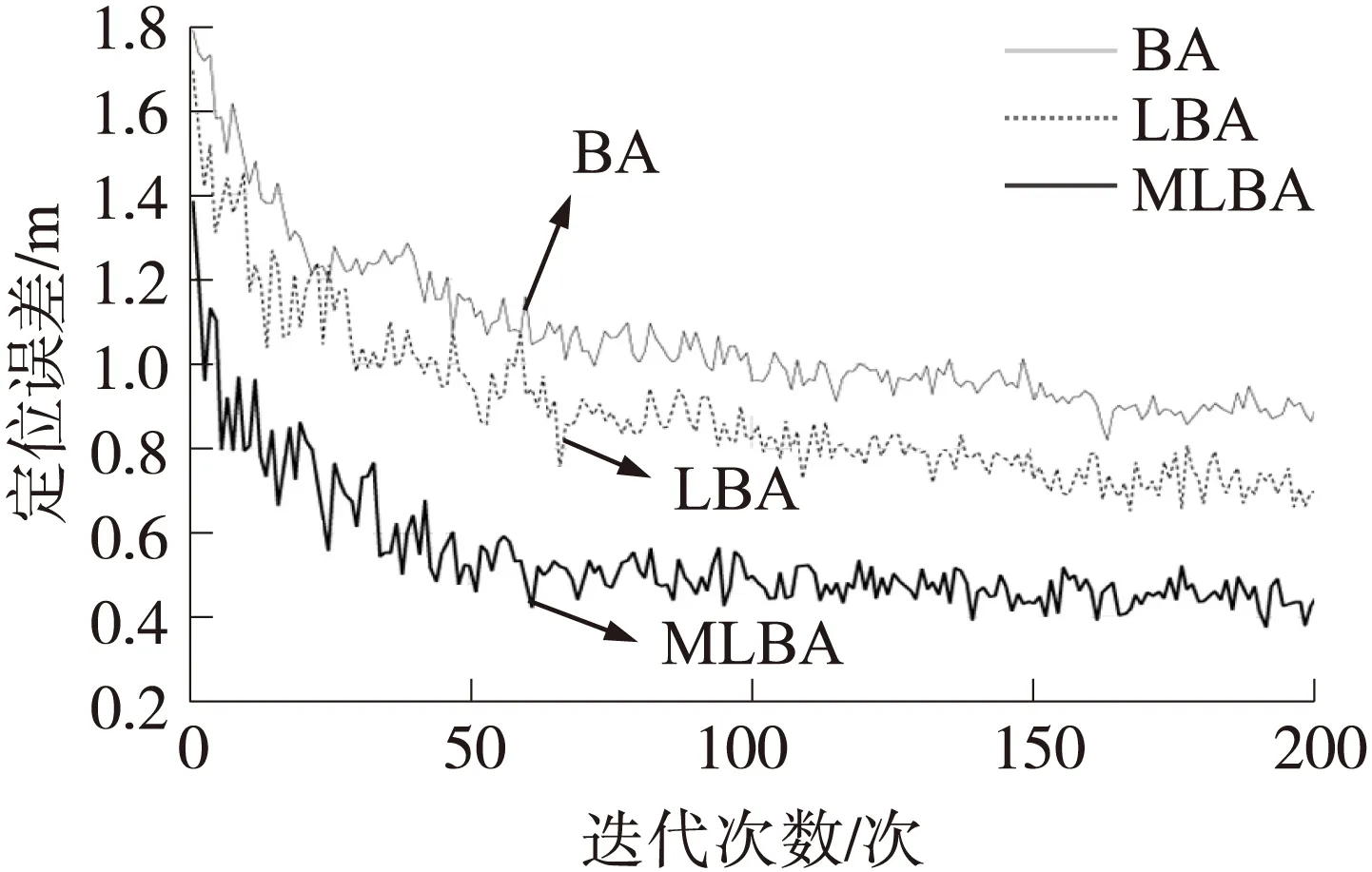
图15 寻优迭代曲线

对于BA、LBA和MLBA算法,统计运算100次的平均定位误差、误差均方差和平均运行时间,实验结果如表3所示。

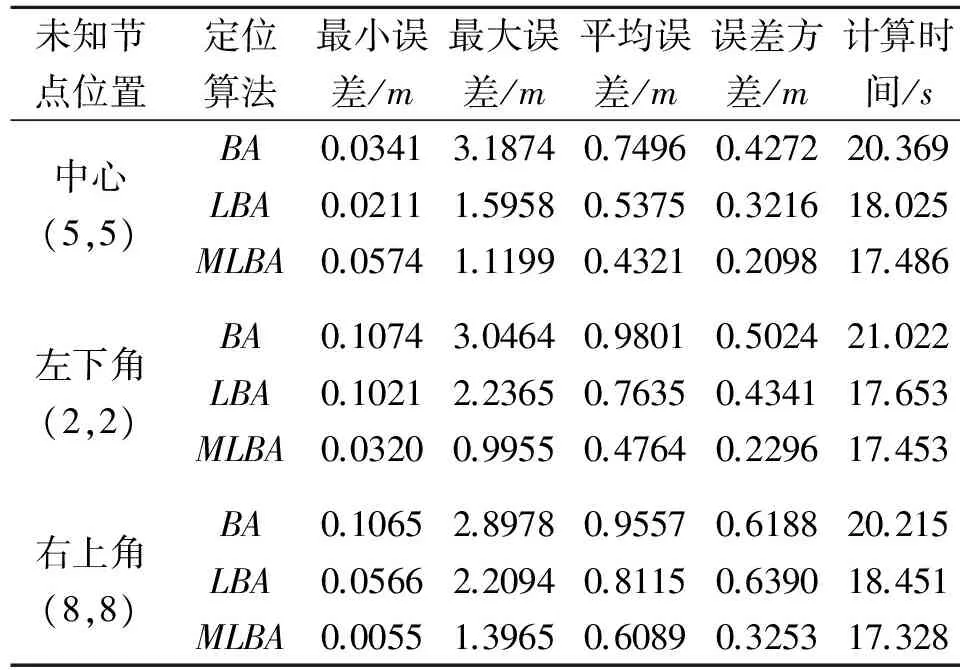
表3 BA、LBA和MLBA算法的性能比较

图6、图9和图12说明:BA算法在定位不同位置节点的时候,都会发生最优解被局部解吸引的情况,基于Lévy飞行特征的算法,寻优性能优于基本的BA算法,是由于Lévy飞行不均匀随机游走的特性,保证了足够的空间搜索,避免局部极值的吸引。如果定位节点在区域的边缘,MLBA算法的定位精度明显优于BA和LBA算法,使用MLBA算法,图11表明全部定位误差小于1m;图14全部定位误差小于1.4m。表3表明,使用3种算法,运行一样的迭代次数,时间上相差不大;MLBA算法的平均定位误差优于BA和LBA算法,MLBA的定位误差的方差也优于BA和LBA算法。

测试3种算法的寻优效率。把定位节点放置在区域中心,测试迭代次数和平均定位误差的关系,实验结果如图15所示。图15中使用BA算法迭代50次,平均定位误差小于1.15m;使用LBA算法平均定位误差小于0.95m;使用MLBA算法平均定位误差小于0.51m;说明:MLAB算法的收敛速度优于BA和LBA算法。

4 结论

为了改进蝙蝠算法在无线传感器的定位性能,本文提出了一种改进的基于Lévy飞行特征的蝙蝠算法,通过修改传统蝙蝠算法中蝙蝠飞行速度和位置的更新方式,使用Lévy飞行拓展搜索空间,避免最优解陷入局部最优,加快了收敛速度。通过比较和分析,表明了MLBA算法具有更快的收敛速度和良好的寻优性能。本文设计的系统实现简单、成本低、运行快,在进行定位计算具有明显的优势,在实际环境的应用中能明显提高节点定位的精度。

[1] Liu Q,Huang X H,Leng S P. Deployment Strategy of Wireless Sensor Networks for Internet of Things[J]. China Communications,2011,8(8):111-120.

[2] Chen C C,Lin T C. A Low-Cost Anchor Placement Strategy for Range-Free Localization Problems in Wireless Sensor Networks[J]. International Journal of Distributed Sensor Networks,2013,2(3):23-30.

[3] Wang S S,Shi K P,Chang C Y. Distributed Direction-Based Localization in Wireless Sensor Networks[J]. Computer Communications,2007,30(6):1424-1439.

[4] Gui L Q,Wei A. Improvement of Range-Free Localization Technology by a Novel DV-Hop Protocol in Wireless Sensor Networks[J]. Ad Hoc Networks,2014,8:1-19.

[5] Xu F C,Liu Z. A New Node Self-Localization Algorithm Based RSSI for Wireless Sensor Networks[C]//Proceedings of the 5th Computational and Information Sciences(ICCIS),Shiyang,China,2013:1616-1619.

[6] Shon M,Minho J,Choo H. An Interactive Cluster-Based MDS Localization Scheme for Multimedia Information in Wireless Sensor Networks[J]. Computer Communications,2012,35(15):1921-1929.

[7] 李论,丁恩杰,郝丽娜,等. 一种改进的煤矿井下指纹定位匹配算法[J]. 传感技术学报,2014,27(3):388-393.

[8] 李牧东,熊伟,梁青. 基于人工蜂群改进算法的无线传感器网络定位算法[J]. 传感技术学报,2013,26(2):241-245.

[9] Wang H C,Wang Y C,Tsai M S. Performance Comparisons of Genetic Algorithm and Artificial Bee Colony Algorithm Applications for Localization in Wireless Sensor Networks[C]//Proceeding of International Conference on System Science and Engineering(ICSSE),Taipei:IEEE Press,2010:469-474.

[10] Yilmaz S,Ugur E,Cengiz Y. Modified Bat Algorithm[J]. Elektronika IR Elektrotechnika,2014,20:1392-1215.

[11] Wang G,Guo L. A Novel Hybrid Bat Algorithm with Harmony Search for Global Numerical Optimization[J]. Journal of Applied Mathematics,2013,9:21-29.

[12] 刘长平,叶春明. 具有Lévy飞行特征的蝙蝠算法[J]. 智能系统学报,2013,8(3):240-246.

[13] Proakis J,Salehi M. Digital Communications[M]. New York:McGraw-Hill Press,2010:165-170.

[14] Yang X S. A New Metaheuristic Bat-Inspired Algorithm[C]//Proceeding of Nature Inspired Cooperative Strategies for Optimization(NISCO 2010)[C]//Springer Berlin,2010:65-74.

[15] Ali E S. Optimization of Power System Stabilizers Using BAT Search Algorithm[J]. International Journal of Electrical Power and Energy Systems,2014,61:683-690.

[16] Shi H X,Ding W J,Yang X S. Bat Algorithm Based on Simulated Annealing and Gaussian Perturbations[J]. Neural Computing and Applications,2014,25(2):459-468.

[17] Mehrdad G,Zahra Z,Yazdan A. Computer Simulation Study of the Lévy Flight Process[J]. Physica A,2009,388:1509-1514.

[18] Viswanathan G M,Afanasyev V,Buldyrev S V,et al. Lévy Flight Search Patterns of Wandering Albatrosses[J]. Nature,1996,381:413-415.

[19] Rhee I,Shin M,Hong S,et al. On the Lévy-Walk Nature of Human Mobility[C]//Proceeding of International Conference on Computer Communications(INFOCOM 2008),Phoenix:IEEE Press,2008:924-932.

[20] Viswanathana G M,Bartumeus F,Sergey V B,et al. Lévy Fight Random Searches in Biological Phenomena[J]. Phusical A,2002,314:208-213.

[21] Selim Y,Ecir U K. Improved Bat Algorithm(IBA)on Continuous Optimization Problems[J]. Lecture Notes on Software Engineering,2013,1(3):279-283.

[22] Viswanathan G M,Afanasyev V,Buldyrev S V. Lévy Fights in Random Searches[J]. Physica A,2000,282:1-12.

[23] Kirkpatrick S,Gelatt C D,Vecchi M P. Optimization by Simulated Annealing[J]. Science,1983,220:671-680.

石 浩(1976-),男,博士研究生,浙江工业大学计算机科学与技术学院,主要研究方向为无线传感器目标定位与跟踪等,constr@163.com;

王万良(1957-),男,教授,博士生导师,浙江工业大学计算机科学与技术学院,研究方向为CIMS、生产计划与调度、智能自动化等,wwl@zjut.edu.cn;

李燕君(1982-),女,副教授,浙江工业大学计算机科学与技术学院,博士,硕士生导师,研究方向为无线传感器路由优化,yjli@zjut.edu.cn。

Bat Algorithm Based on Lévy Flight Feature and ItsLocalization Application in WSN*

SHIHao,WANGWanliang*,LIYanjun,LULiangjin

(College of Computer Science and Technology,Zhejiang University of Technology,Hangzhou 310023,China)

Given the shortcomings of premature convergence and slow convergence speed in bat algorithm,an improved adaptive bat algorithm(BA)based on Lévy flight strategy characterized by heavy-tailed distribution is proposed,which differs traditional BA in update approach of bat’s flying velocity and positions. It could effectively keep from the algorithm into a local optimum and accelerate convergence to achieve a balance between exploration and exploitation mechanisms. In WSN applications,we converted the WSN location problems into the global optimization ones and by applying ZigBee hardware platform to compare with other algorithms in different position,a conclusion could be drawn that the improved algorithm is of quicker convergence speed and higher precision,moreover,which realizes simple condition,high accuracy with huge value of practical engineering applications.

wireless sensor network;RSSI;localization algorithm;bat algorithm;Lévy flight

项目来源:“十二五”国家科技支撑计划项目(2012BAD10B01)

2014-11-27 修改日期:2015-03-12

C:6150P;7230

10.3969/j.issn.1004-1699.2015.06.019

TP393;TN98

A

1004-1699(2015)06-0888-07