微机械振动电场传感器闭环自激驱动建模及系统仿真*

刘 恒,熊 丰,孟瑞丽,2,张宏群

(1.南京信息工程大学电子与信息工程学院,南京 210044;2.南京信息工程大学教务处,南京 210044)



微机械振动电场传感器闭环自激驱动建模及系统仿真*

刘 恒1*,熊 丰1,孟瑞丽1,2,张宏群1

(1.南京信息工程大学电子与信息工程学院,南京 210044;2.南京信息工程大学教务处,南京 210044)

本文针对微机械振动电场传感器灵敏度受驱动控制电路参数和谐振频率漂移影响问题,利用平均周期法对不同闭环自激驱动下微机械电场传感器的灵敏度进行了建模分析,理论和仿真分析表明:加入满足约束条件的PI控制器,灵敏度变化与屏蔽层固有谐振频率漂移和品质因数变化无关;加入满足约束条件的PI控制器比没有PI控制器的灵敏度大;PI控制器的参数不满足约束关系,输出电压不稳定,输出失真。

电场传感器;自激振荡;灵敏度;平均周期法

微机械谐振式传感器是通过频率来敏感外部非电量信息,电场传感器在大气电场探测、电力、气象和地震等领域具有重要的应用,空中大气电场的探测,可用于保障火箭、卫星等飞行器的升空安全等。采用硅微机械加工技术制备的微型电场传感器由于在成本、体积、功耗和集成化等方面具有明显优势,逐渐成为研究热点[1-3]。理论分析表明,微机械电场传感器的灵敏度与屏蔽层的微结构的振动幅度和谐振频率的乘积有关,乘积越大,灵敏度越大;同时,在传感器长期使用过程中,材料疲劳等引起的机械刚度发生变化,屏蔽层微结构的固有谐振频率会发生漂移,对应的振动幅度和频率乘积变化会引发灵敏度的突变,输出非线性度增大[4-6]。加之器件尺寸小,空间耦合干扰大,有效信号微弱,极易受到噪声、外部干扰的影响,这就需要提供稳定、可靠的驱动电压以激励振动梁振动,保证振动幅度和频率乘积不变。

目前,在微机械谐振传感器的驱动控制中,多采用自激驱动控制或锁相环技术来实现驱动能量变化频率对敏感元件振动频率的跟踪[7-8]。自激驱动控制利用上电随机噪声来激励敏感元件,通过不断反馈来增大驱动能量。文献[7]给出了一种闭环自激驱动方案,并通过数值仿真分析了频率漂移对灵敏度的影响,但并未从理论上分析灵敏度误差大小与控制电路参数、频率漂移等的数值关系。文献[8]给出了一种闭环自激驱动控制方案及分析仿真实验,但接口电路采用的电荷放大器,以振动幅度恒定为控制目标,并未考虑频率漂移、直流参考电压等对灵敏度非线性影响。本文以跨阻放大器为接口电路,推导了微机械振动式电场传感器灵敏度的表达式,然后建立了两种闭环驱动下的传感器系统动力学模型,鉴于系统的高阶非线性,利用平均周期法分析了不同驱动方式下,灵敏度受扰动后的非线性误差大小,并最终确定了闭环驱动系统的验证数值模型,通过仿真确定了灵敏度与直流参考电压VR、检测电容加载的直流电压和跨阻放大器的电阻等的关系。为后续的微机械电场传感器测控电路的设计及调试提供理论基础。

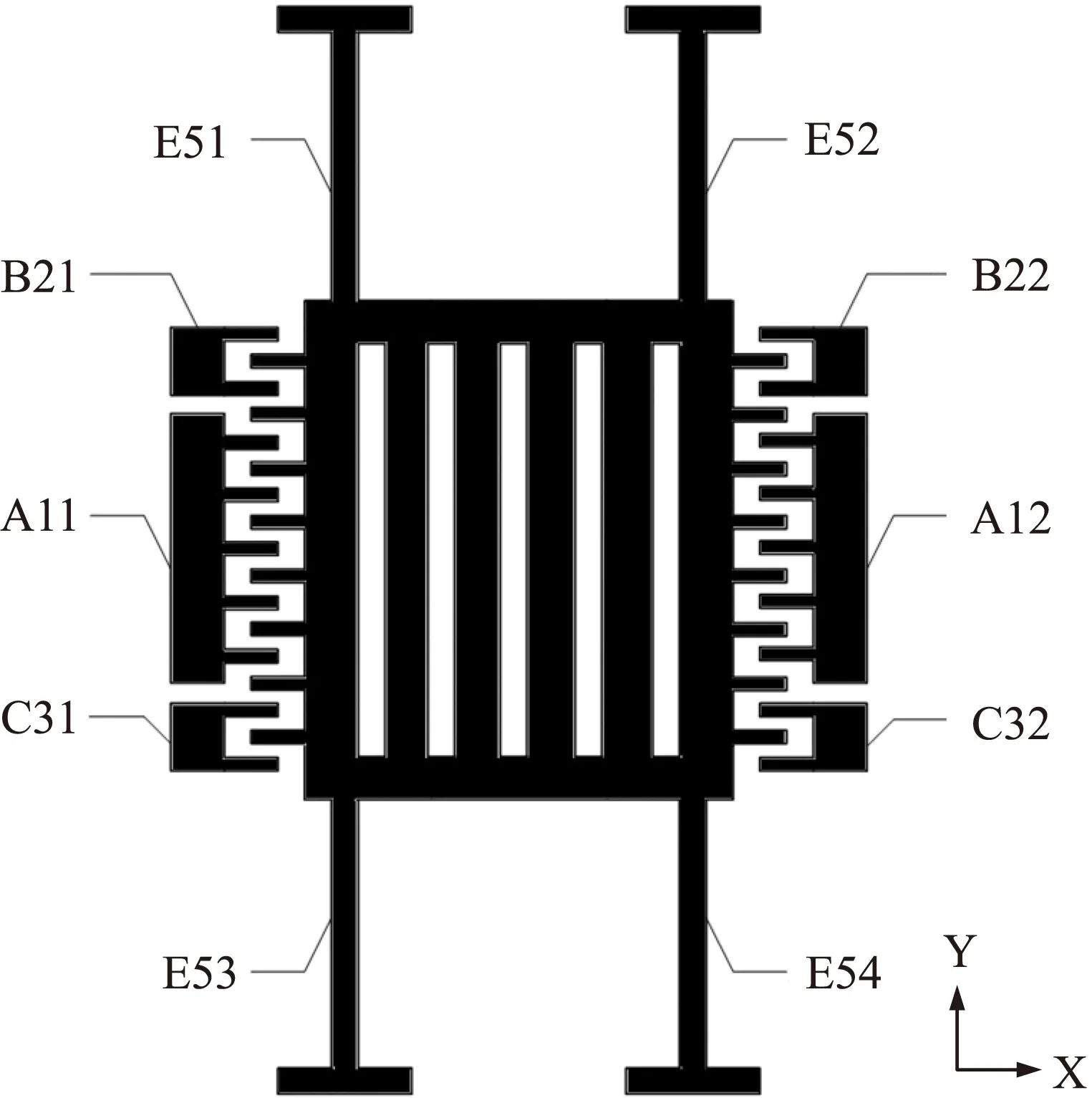
图1 微机械电场传感器屏蔽结构层示意图

1 微机械电场传感器的原理

面内振动的微机械电场传感器主要包括屏蔽结构层和感应电极层,屏蔽层结构水平方向运动周期的遮盖下面的敏感电极,使得感应电极表面上的感生电荷量发生周期性变化,因而接口电路中产生与外界电场成比例的交变电流[7-8]。图1为对应的微机械电场传感器的屏蔽结构层,活动结构E5包括一个中心设置有间隙的矩形质量块、设置在质量块四周的梳齿,与质量块4个端角相连接的支撑梁E51、E52、E53、E54。固定梳齿A11、A12为差分驱动梳齿,固定梳齿B21、B22、C31、C32为差分检测梳齿。

图2为传感器的电极敏感层,包括差分电极F61和F62。

图2 微机械电场传感器敏感电极层示意图

根据高斯定理,在屏蔽层可动结构周期屏蔽感应电极模式,感应电极电流信号经过I-V转换、放大、滤波等之后,用激励信号作为电场解调的参考信号,经过相关解调和低通滤波后,解调出的电场强度对应的输出电压值为[7-8]:

V0=HωnXE

(1)

式(1)中:H为电路参数决定的常量,不能任意增大,太大电路输出电压就达到饱和,ωn为屏蔽层可动结构的谐振频率,X为振动幅值。根据式(1)可知,振动频率ωn和振动幅值X乘积与灵敏度有关。因此,在材料疲劳及扰动下,激励电压应该实时跟踪结构谐振频率的变化,确保振动幅度和谐振频率的乘积不变,这不同于单一幅度X恒定振动控制要求[7-8]。

2 基于自激原理的微机械电场传感器闭环控制

真空封装下微机械电场传感器系统品质因数大,基于跨阻放大器的静电自激驱动包括振动位移与检测电容的转换,跨阻放大器,全波整流,低通滤波器,反相加法电路等构成。接口采用了梳齿电容差分形式,检测电容ΔC有:

(2)

式中:N为检测梳齿对数,ε为介电常数,L为检测梳齿初始交叠长度,d为检测梳齿间距。跨阻放大器将电容的变化转换为电压的变化,输出电压V1为:

(3)

式中:R为跨阻放大器的电阻,Vdc为直流参考电压,k1为等效增益系数,k1=-2RNε/d。梳齿A11加载电压Vd+Vasin(ωt),梳齿A12加载电压Vd-Vasin(ωt)。屏蔽层的质量块接地,质量块受力为:

(4)

式中:N0为驱动梳齿对数,d0为驱动梳齿间距。k2为等效增益系数,k2=4N0ε/d0。

整个控制系统包含一个自动增益控制AGC(AutoGainControl)环路,见图3。首先通过跨阻放大器得到输出电压V1,一路再通过全波整流和低通滤波器,τ为一阶低通滤波器的时间常数,得到的直流电压A与负参考直流电压-VR进行反相加法运算,差压Vc再通过PI控制器作为驱动电压中的直流部分,kp和kI分别为控制器的比例和积分系数。另一路直接与直流电压叠加在一起,作为驱动电压。文献[7]对应的控制系统没有PI控制器,控制目标是实现振动幅度恒定。根据实验发现,由于材料的疲劳、温度等的变化,微结构的谐振频率会发生变化,单一的恒幅控制会带来灵敏度的非线性。本文通过理论推导分析没有和有PI控制器下,微机械电场传感器的灵敏度的变化。

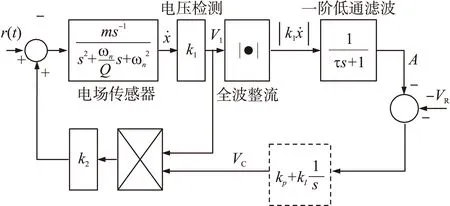
图3 微机械电场传感器闭环自激控制

在没有PI控制器时,根据静电驱动动力学原理,建立方程为:

(5)

假定微结构位移为x(t):

x(t)=a(t)cos[ωnt+φ(t)]

(6)

式中:a(t)和φ(t)为振动位移的幅度和相位,a(t)=X,结构谐振时,ω=ωn,可以认为是两个缓变参数[9-10]。振动速度为位移的导数,有:

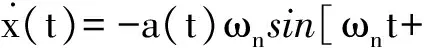
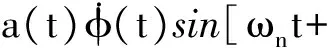
(7)

由于幅度变化和相位变化为缓慢变化参数,有:

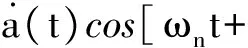
(8)

那么振动加速度为:

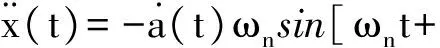
a(t)ωn[ωnt+φ(t)]cos[ωnt+φ(t)]

(9)

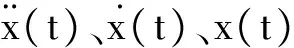
(10)

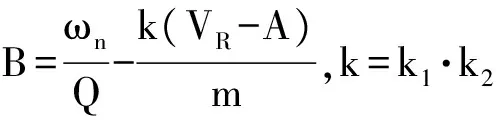
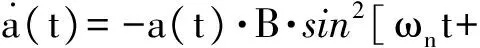
(11)

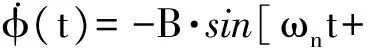
(12)

(13)

对于慢时变系统,根据平均周期法原理,有[11-12]:

将上述表达式代入式(11)、(12),有系统两个平衡点:

(14)

(15)

分析式(15)知:

(16)

理论推导结果表明:文献[7]报道的没有PI控制器自激闭环系统在频率发生漂移时,无法实现灵敏度的不变,灵敏度的非线性大小与式(16)各参数取值有关。

图3所示闭环控制系统加入PI控制器后,系统的动力学方程表示为:

(17)

利用平均周期法原理,化简方程组(17),得到新的稳定平衡点表示为:

(18)

分析式(18)知:

(19)

在该平衡点附近对方程组(18)进行线性化,得到方程经过拉普拉斯变换后的特征方程为:

(20)

要使系统稳定,根据劳斯判据,得到系统的稳定条件为:

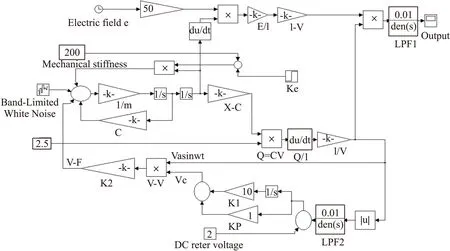
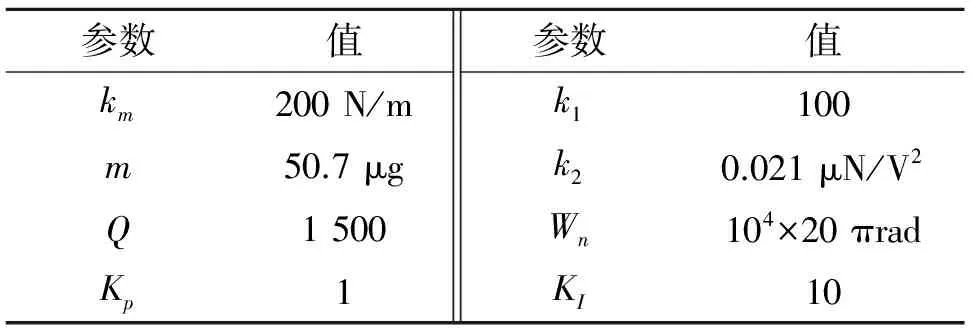
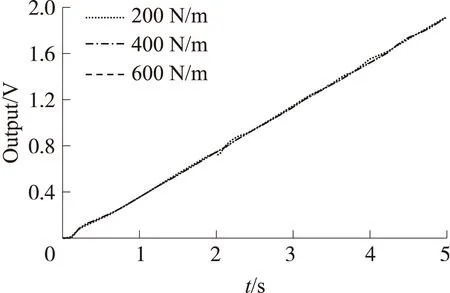
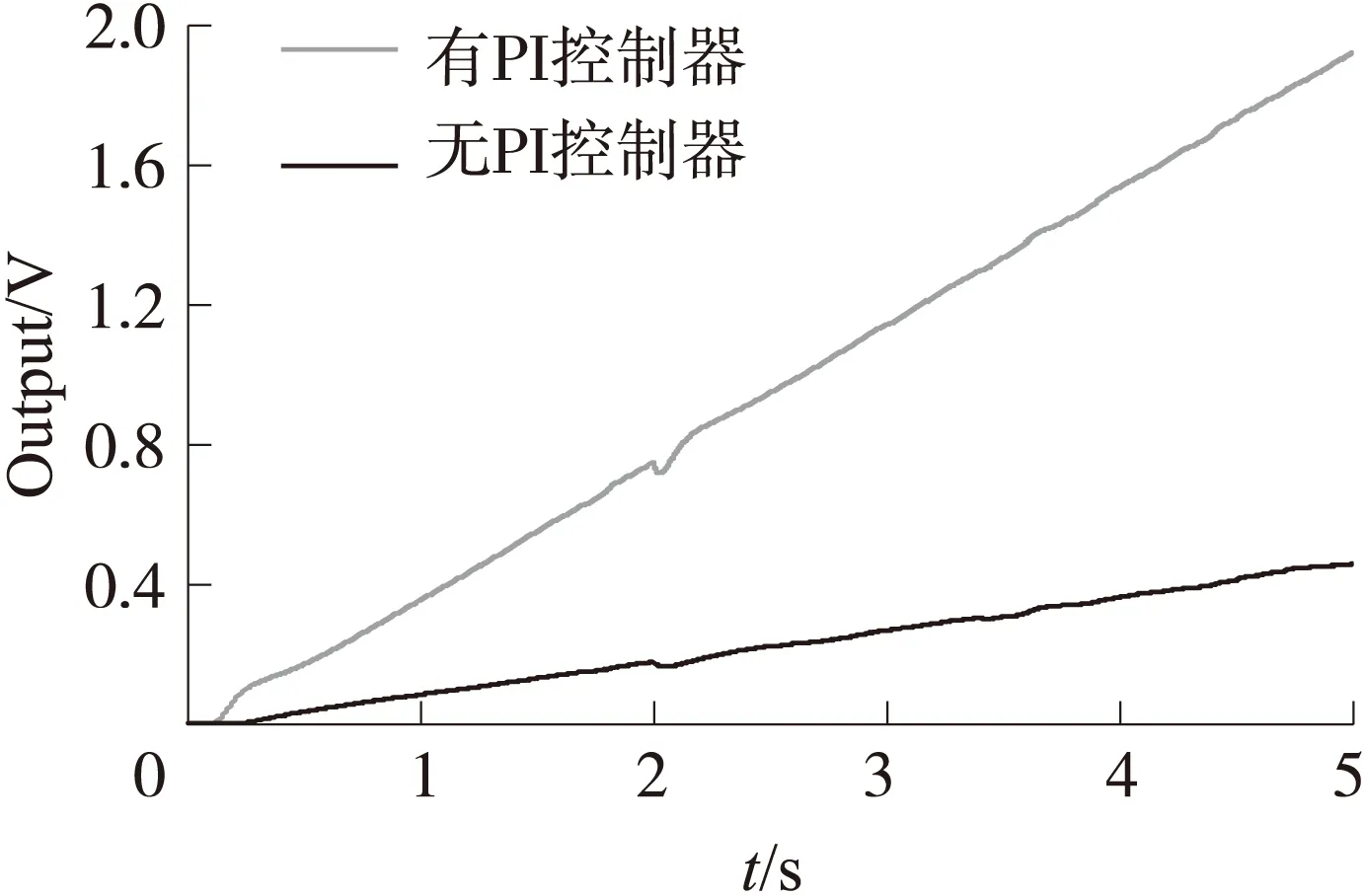
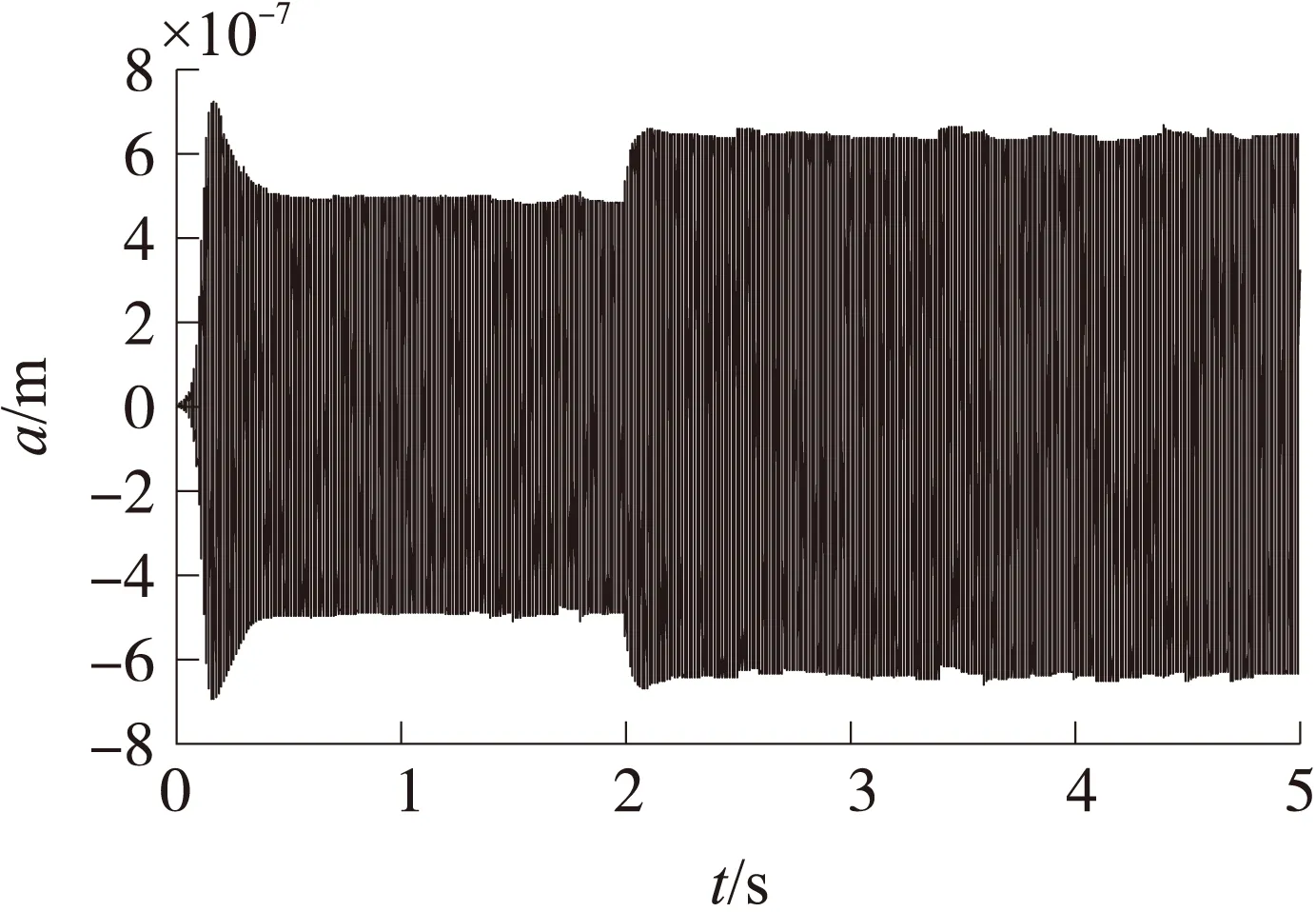
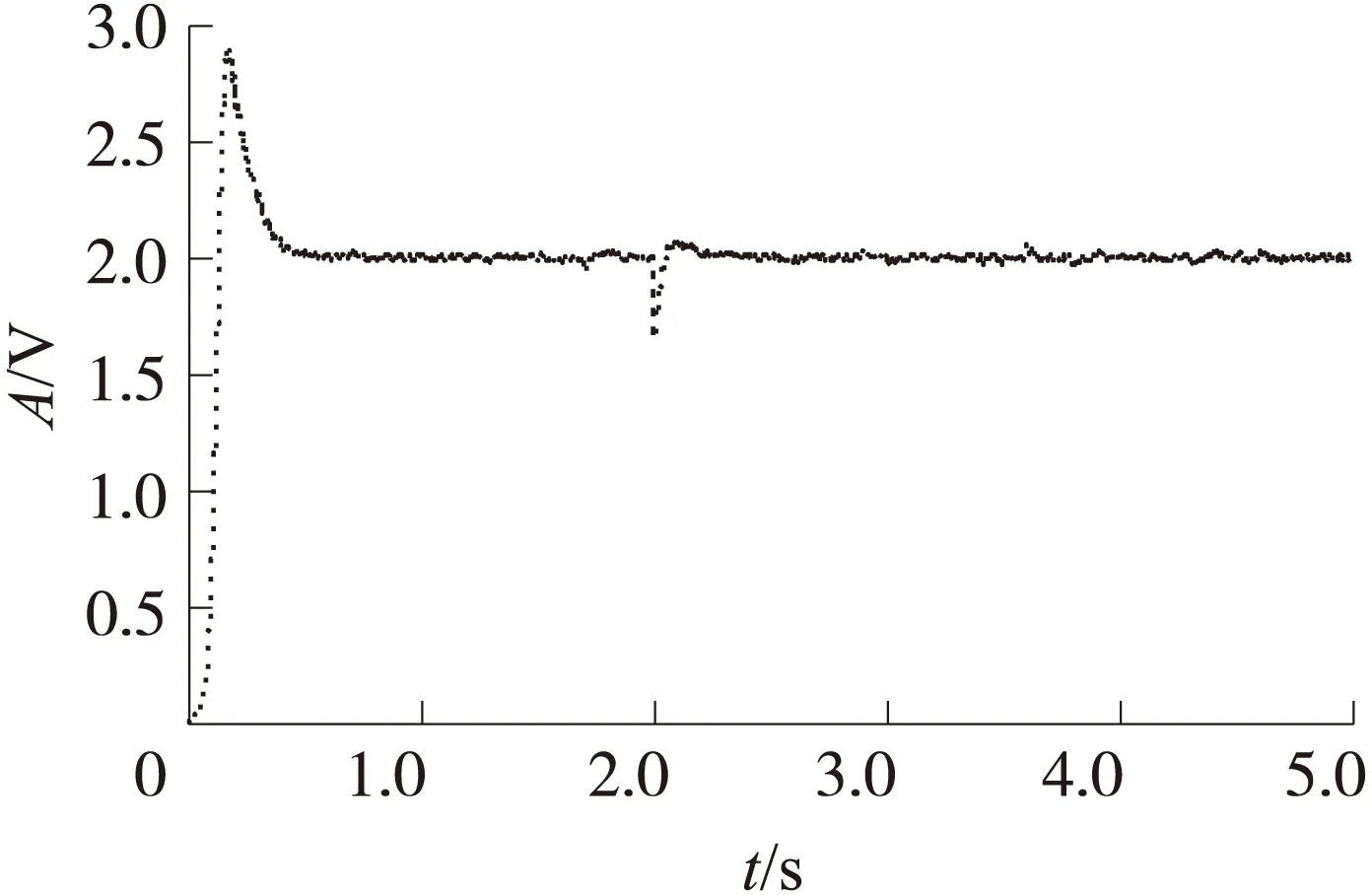
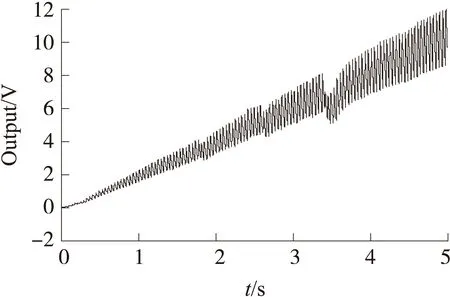
kI

(21)

根据式(19)知,加入PI控制器后,稳态灵敏度与直流参考电压VR和等效增益系数k1=2RNε/d有关,与品质因数Q、谐振频率无关。在温度变化时,结构材料的杨氏模量和振动梁的刚度会发生变化,谐振频率会发生漂移,但此时灵敏度将不发生变化。根据式(21),系统能够稳定收敛,需要控制器系数满足约束条件。

3 微机械电场传感器的驱动数值仿真

为了对自激驱动理论分析进行验证,本文利用设计的微机械电场传感器结构参数在MATLAB/SIMULINK下建立了对应的仿真模型。加工的微机械电场传感器采用了金属圆形储能焊真空封装,测得的品质因数为1 500左右。整个闭环自激驱动电路见图4,由于振动结构在长期的振动中频率会发生漂移[13],仿真中ke为刚度扰动信号,在仿真时间为2s时,ke从0阶跃变化为80N/m。表1给出了仿真的参数值,直流参考电压VR为2V,大于没有PI控制器的临界起振参考电压VR0=1V,系统能够起振。τ为0.001,根据表1,kp、kI及τ满足系统稳定条件。

图4 微机械电场传感器自激驱动仿真模型

参数值参数值km200N/mk1100m50．7μgk20．021μN/V2Q1500Wn104×20πradKp1KI10

仿真中,为了模拟自激过程,加入了白噪声等效的静电力,在整个仿真时间5 s内,白噪声等效的静电力N为随机大小,数量级为10-9N。对应的静电驱动力Fd大小在10-7N数量级,远大于白噪声等效的静电力N。对于灵敏度的仿真验证,采用了相关解调和低通滤波方法[6-7],所有仿真对应的电场从0均匀变化到250 V/m,忽略接口电路的噪声影响。在上述条件下,对应的输出电压与输入电场的比即为灵敏度,图5给出了不同屏蔽层刚度km对应的输出电压,在PI控制器存在,且满足约束条件时,当km分别为200、400和600 N/m,对应的输出电压轨迹线重合,这与式(19)相一致,在质量不变情况下,灵敏度的大小与谐振频率无关,温度对材料的影响几乎不会改变灵敏度。

图5 不同屏蔽层结构刚度下的输出电压

图6为相同条件下有PI控制器和无PI控制器对应的输出电压,在刚度突变过程,输出电压在2 s时均会进入下降过渡区域,在自动增益控制环路下,最终达到稳定输出,但很显然,在相同直流参考电压VR作用下,没有PI控制器,在0～250 V/m范围内,输出电压为0～0.45 V;加入满足约束条件的PI控制器,在0～250 V/m范围内,输出电压为0～1.90 V,这表明:加入PI控制器,电场传感器灵敏度比没有PI控制器的灵敏度大322%。

图6 微机械电场传感器有和无PI控制器对应输出电压

图7 微机械电场传感器有PI控制器对应振动幅度

为了验证平均周期法分析的理论结果与仿真结果是否一致,图7和8为仿真对应的有PI控制器对应的振动幅度和检测直流电压。根据式(18),在刚度突变前,理论计算得到的振动幅度为0.5 μm,突变后,幅度变化为原来的1.291倍,也就是0.645 5 μm。而检测直流电压A理论计算为VR,也就是2 V。上述理论计算结果与仿真稳态结果一致,证明了平均周期法分析系统行为的有效和准确性。

PI控制器能够稳定系统,需要满足约束关系式(21)。图9对应的τ为0.001,与前述仿真一致。kI为1 500,kp为1,不满足约束式(21)。图9对应的输出电压呈现发散趋势,输出电压噪声越来越大,对应的灵敏度也无法收敛,传感器的输出失真。

图8 微机械电场传感器有PI控制器对应检测直流电压

图9 PI控制器不满足约束条件对应输出电压

4 结论

针对已有文献关于微机械振动式电场传感器的驱动控制中存在的灵敏度随谐振频率漂移而非线性增大问题,本文将自激恒定幅度控制变为振动速度恒定控制,鉴于系统的高阶非线性,利用平均周期法分析了闭环系统的行为。理论和仿真实验表明:①加入满足约束条件的PI控制器,灵敏度变化与屏蔽层固有谐振频率漂移和品质因数变化无关;②加入满足约束条件的PI控制器比没有PI控制器的系统灵敏度大;③振动幅度和直流检测电压的理论分析和数值仿真对比表明:平均周期法分析系统的行为是有效准确的;④PI控制器的参数不满足约束关系,将带来输出电压不稳定,输出失真。

[1] 郑凤杰,夏善红,陈贤祥,等. 三维电场传感器仿真优化及性能测试[J]. 传感技术学报,2008,21(6):946-950.

[2] 彭春荣,刘世国,张海岩,等. 新型推挽激励的谐振式微机械静电场传感器[J]. 纳米技术与精密工程,2010,8(4):341-345.

[3] 杨鹏飞,彭春荣,张海岩,等. SOI微型电场传感器的设计与测试[J]. 电子与信息学报,2011,33(11):2771-2774.

[4] Peng Chunrong,Yang Pengfei,Guo Xin. Measuring Atmospheric Electric Field Using Novel Micromachined Sensor[C]//Proceedings of the 6th IEEE International Conference on Nano/Micro Engineered and Molecular Systems,Kaohsiung,Taiwan. 2011:417-420.

[5] Gayan Wijeweera,Behraad Bahreyni,Cyrus Shafai,et al. Micromachined Electric-Field Sensor to Measure AC and DC Fields in Power Systems[J]. IEEE Transactions on Power Delivery,2009,24(3):988-993.

[6] Behraad Bahreyni,Gayan Wijeweera,Cyrus Shafai,et al. Analysis and Design of a Micromachined Electric-Field Sensor[J]. Journal of Microelectromechanical Systems,2008,17(1):31-36.

[7] 熊幼芽,彭春荣,夏善红. 一种闭环自激式驱动的硅微机械电场传感器[J]. 电子与信息学报,2009,31(11):2776-2780.

[8] 刘恒,孟瑞丽,孙冬娇. 一种微机械电场传感器的驱动控制及数值仿真[J]. 传感技术学报,2013,26(4):509-515.

[9] Liu Heng,Su Wei,Zhang Futang. Oscillation Loop for a Vibratory Gyroscope and Its Experiment[J]. Journal of Dynamic Systems,Measurement and Control,2012,134(1):1104-1111.

[10] 刘恒,何晓平,张凤田,等. 基于平均周期法的谐振微加速度计驱动控制研究[J]. 控制理论与应用,2011,28(10):1261-1268.

[11] 王展飞,鲁文高,李峰,等. MEMS振动陀螺闭环自激驱动的理论分析及数值仿真[J]. 传感技术学报,2008,21(8):1337-1342.

[12] Sun X,Horowitz R,Komvopoulos K. Stability and Resolution Analysis of a Phase-Locked Loop Natural Frequency Tracking System for MEMS Fatigue Testing[J]. Journal of Dynamic Systems,Measurement and Control,2002,12:599-605.

[13] 董林玺,俞权,包金艳,等. MEMS圆盘谐振器形变对电气刚度影响分析[J]. 传感技术学报,2014,27(7):881-885.

刘 恒(1980-),男,讲师,博士,主要研究方向为微机械惯性传感器结构设计及信号处理,ghost80boy@163.com;

熊 丰(1990-),男,硕士研究生,主要研究方向为微机械谐振传感器结构设计及测试,xf1990719@163.com;

孟瑞丽(1984-),女,硕士研究生,主要研究方向为微机械谐振传感器设计及测试,1960673295@qq.com。

Modeling and Numerical Simulation of Closed-LoopControl for an Electric Field Micro-Sensor*

LIUHeng1*,XIONGFeng1,MENGRuili1,2,ZHANGHongqun1

(1.School of Electronic and Information Engineering,Nanjing University of Information Science and Technology,Nanjing 210044,China;2.Dean’ss Office,Nanjing University of Information Science and Technology,Nanjing 210044,China)

Because sensitivity of a micro mechanical resonant electric field sensor is influenced by the parameters of driving circuit and drift error of resonance frequency,a dynamic model was built for the micro sensor,and it analyzed the system behavior and sensitivity on different closed loop self-excited circuits using averaging method in this paper. Theory and simulation results show that with the help of PI controller,the sensitivity is constant regardless of variations in shielding layer resonance frequency and Q-factor;the sensitivity with a suitable PI controller is larger than the sensitivity without a PI controller;if the parameters of PI controller do not satisfy the constraint relationship,output voltage is not stable and the sensitivity is distortion.

electric field micro-sensor;self-oscillation;sensitivity;averaging method

项目来源:江苏省自然科学基金项目(BK20131001);江苏省高校自然科学研究基金项目(13KJB510017);制造过程测试技术-省部共建教育部重点实验室开放基金项目(14zxzk02)

2015-01-07 修改日期:2015-02-14

C:7630

10.3969/j.issn.1004-1699.2015.06.009

TN911.71

A

1004-1699(2015)06-0825-06