如何在课堂教学中让学生领悟数学思想——以“推理能力”的获得为例

安徽天长市城南小学（239300） 卢杰夫

数学课程标准指出：“数学思想”是对数学知识的本质认识，是从某些具体的数学内容和对数学的认识过程中提炼、上升的数学观点，它在认识活动中被反复运用，带有普遍的指导意义，是建立数学和用数学解决问题的指导思想，它主要是指数学抽象的思想、数学推理的思想和数学模型的思想。本文主要结合相关案例谈一谈“推理思想”（主要包括演绎推理和归纳推理两种）在数学教学中的运用，并指导学生学会使用推理的方法解决数学中的问题，积累数学活动的经验。

一、“推理思想”在课堂中的运用

通过对教材的分析，笔者发现在小学数学教材中，使用“推理”方法解决问题的案例有很多。

例如，长方形面积计算公式的归纳。

在课程标准的理念指导下，大部分教师都能革新观念，不再生搬硬套，直接告诉学生图形的面积计算公式，而是让学生参与数学学习的过程，通过举例归纳或者动手“剪一剪”、“移一移”、“拼一拼”的活动，来获得图形的面积计算公式。

活动：用12个面积是1平方厘米的小正方形拼成一个长方形，你能拼出几种情况？

学生动手拼一拼：

教师将学生的拼图情况列在表格里，方便观察。

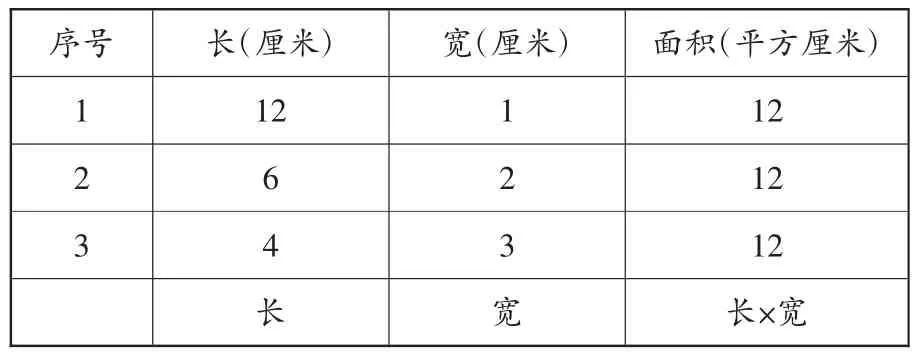
序号 长（厘米） 宽（厘米） 面积（平方厘米）1 12 1 12 2 6 2 12 3 4 3 12长宽长×宽

显然，通过不同的情况来归纳出长方形的面积公式，是推理思想在数学教学中的有效运用。

又如，平行四边形面积公式的推导。

活动：把平行四边形剪一刀，变成长方形。

学生操作，师提问：

1.你是沿着哪条线把平行四边形剪开的？（高）

2.剪开后你是怎样拼成长方形的？（平移）

（学生边回答，教师边演示，如下图）

3.平行四边形转化成长方形后，什么变了，什么没变？（形状变了，面积不变）

4.长方形的长与宽分别与平行四边形的底和高是什么关系？（长方形的长就是平行四边形的底，长方形的宽就是平行四边形的高）

5.根据这些条件，你能推导出平行四边形的面积计算公式吗？（平行四边形的面积＝底×高，即S＝ah）

由上面两个例子可以看出“，推理思想”在小学数学中的重要作用。因此课程标准在课程总体目标的数学思考部分做了如下的要求：“经历观察、实验、猜想、证明等数学活动过程，发展合情推理的能力和初步的演绎推理能力，能有条理地、清晰地阐述自己的观点。”

二、学生推理能力的培养

根据标准要求，掌握比较完善的推理能力是儿童智力发展的重要环节和主要标志，数学教学中应注意培养和发展儿童的推理能力。那么如何帮助小学生获得推理能力呢？

1.从学生熟悉的生活场景中培养学生的推理能力

爱因斯坦说过“：兴趣是最好的教师。”从学生最熟悉的生活情景入手，让学生产生共鸣，激发学生学习的兴趣，体现数学源于生活的理念，同时让学生感受到数学是有“用”的。在学生熟悉的生活场景中培养学生的推理能力，学生可以更轻松地吸收和掌握。

例如，习题：一根旗杆的高度是15（ ）。这题的答案要么是米，要么是厘米。学生看到这样的题目，首先想到的是学校里的旗杆，那是很高的，如果填厘米的话，那么15厘米还没有自己的尺子长，显然是太短了，所以旗杆的高度是15米。

又如，习题：小朋友每天在校时间大约是6（ ）。答案到底是什么呢？学生利用自己知道的时间来推理：小朋友一节课的时间是40分，学生一天在校时间肯定比一节课的时间长，因为一天要上6节课，所以6分和6秒都不行，只能填6时。

这两个例子都是与学生日常生活密切相关的，学生利用自己的知识进行对比，从而推出正确的结果，培养了自身的推理能力。

2.把推理能力的培养融合在数学教学的过程中

课程标准把推理能力的培养落实到“数与代数”、“图形与几何”“、统计与概率”“、综合与实践”四个领域的内容当中，这四个领域都为发展学生的推理能力提供了很好的素材，改变了过去认为只有在几何证明时才能培养学生的推理能力的现象。

在“数与代数”的教学中，教师给学生提供足够的时间和空间，组织学生经历观察、实验、猜想、证明等教学活动，并把推理能力的培养有机地融合在这样的过程中。例如：从除法中的“除数不能为零”推出分数中“分母不能为零”，推出“比”的“比的后项不能为零”；从除法中商不变的性质中推出分数的基本性质；等等。

在“图像与几何”这部分内容的教学中，主要通过“剪一剪”“、拼一拼”“、折一折”等的活动感知图形的性质，如在探索图形的面积的求法时，总要联系或者转化成已知的图形，然后推出新的图形的面积的算法，如“平行四边形”的面积计算公式。

在“统计与概率”的教学中，概率知识的学习可以提高学生的归纳推理能力。如，在“可能性”相关知识的教学中，让学生判断摸出哪种颜色的球的可能性大，这需要多次的操作和记录。最后通过分析记录的数据，然后进行归纳总结，得出结论。

在“综合与实践”这部分内容中，同样可以培养学生的推理能力，如“估计一本童话故事书有多少字”这一实践活动就需要学生利用自己已有的知识，计算出一页的字数，再推算出整本书的字数。

下面将以“乘法分配律”的教学为例，谈一谈如何在课堂教学中培养学生的推理能力。

1.提出问题

师：每件夹克衫65元，每条裤子45元，大家算一算，要买5件夹克衫和5条裤子，一共要付多少元？

2.学生计算后汇报

生1：先分别算出5件夹克衫的钱和5条裤子的钱，再将两个钱数合起来，算式是“65×5＋45×5”。

生2：先算一套衣服的钱，再算5套衣服的钱，算式是“（65＋45）×5”。

3.猜一猜

师：有两种不同的算法，得到两个不同的算式，大家猜一猜，这两个算式的结果会怎么样？

生：结果相等，也就是说“（65＋45）×5＝65×5＋45×5”。

4.验证

师：是否相等呢？动手算一算。

生1：两个算式的结果都是550，等式是成立的。

师：观察等式两边数字的特点，仿照这样的写法，自己写两个算式，并验证，看这样的等式是否具有普遍适用性。

生2：（10＋2）×5＝60，10×5＋2×5＝60，（10＋2）×5＝10×5＋2×5。

生3：（4＋2）×25＝150，4×25＋2×25＝150，（4＋2）×25＝4×25＋2×25。

……

5.归纳，概括

根据学生对不同例子的验证，可以概括出“乘法分配律”的一般性表述：两个数的和与第三个数相乘，等于这两个加数分别与第三个数相乘后的和。用字母表示就是“（a＋b）×c＝a×c＋b×c”。

在学习乘法分配律时，教师没有直接给出结论，而是通过学生的“猜测——验证——归纳”而得，体现了推理的方法在课堂教学中的具体运用，也有助于学生推理能力的培养。

三、从探索规律中培养学生的推理能力

探索规律是一个发现关系、发展思维的过程，在探索规律的过程中，学生需要经历观察、猜想、归纳、验证的过程，这有利于培养学生的推理能力。

例如，几十一乘几十一的乘法速算规律。

1.观察下面的算式和结果，你有什么发现？

11×11＝121；21×41＝861；31×41＝1271；51×61＝3111。

2.讨论：算式的特点和积的规律。

十位和十位相乘放在首，个位和个位相乘放在尾，十位和十位相加放中间。

3.用发现的规律做下面各题：

21×21；61×81；41×41。

4.利用两位数乘两位数的竖式计算验证结果是否正确。

这个例子是在学习了两位数乘两位数的基础上，引导学生来探索特殊类型乘法算式速算的规律。首先引导学生观察算式，概括出特征，然后发现积与乘数之间的关系，提出猜想，再通过举例，验证猜想，表达发现的规律。在这个探索规律的过程中无疑提高了学生的数学推理能力。

在整个义务教育阶段，对学生推理能力的培养是内容学习和目标达成的一条主线，也是一个逐渐提升的长期过程。对于推理能力的培养，更偏向于一种方法的获得，而作为一种方法，是不具有普遍适用性的，数学的推理思想是全面的，普遍的，因此教师在讲授推理方法时要尽量反映和体现推理思想，让学生了解和体会推理思想，提高学生的数学素养。