基于功率谱估计的双液压马达同步系统实验研究

， ， 　(.中国煤炭科工集团 太原研究院有限公司， 山西 太原　030006；.神华神东煤炭集团有限责任公司， 陕西 榆林　7935； 3.中国矿业大学， 北京　00083;4.中国煤炭科工集团有限公司， 北京　0003)

引言

双液压马达同步驱动系统常用于负载惯量大，加速度要求高等大功率应用场合，以减小设备整体重量和尺寸，增加结构刚度。同步驱动主要有三种控制方式：等同式、主从式和交叉耦合式。等同式中，各运动控制通道之间无控制策略方面的耦合， 各控制通道同时动作实现同步，同步误差取决于各控制通道之间的动态性能偏差。主从式以动态响应较慢的控制通道作为主回路，以动态响应较快的控制通道为从回路，跟随主回路动作。交叉耦合式在等同式的基础上，将两控制通道的输出误差加权后叠加到控制器输出端， 以获得更高的运动精度。由于控制系统中各元部件在不同工况下动态特性参数的非线性、时变性，同步控制一直是困扰学术界和工程应用领域的一个主要问题，国内外学者都对同步控制问题进行了大量研究工作。

国内同步控制研究中，赵克定等[1]介绍了双电液伺服马达同步控制系统的共反馈共校正，分反馈分校正，共反馈同步误差校正，主/辅控制单边校正以及状态差值反馈最佳控制等方案。李军伟等[2]在三轴仿真转台上进行了等同式控制方案的实验研究，结果表明等同式控制方案具有较高的控制精度。王凯[3,4]等利用神经网络和模糊控制方法能很好地克服液压系统非线性的特点，将其应用于仿真转台的同步控制和干扰抑制中。王益群等[5]使用了多输入多输出(MIMO)H∞和QFT方法来设计同步控制器，以从整体上提高多通道电液伺服系统的同步性能。国外对同步控制研究较早，Sarachik等[6]首先提出了非对称交叉耦合式同步控制方案。Koren等[7,8]在CNC机床同步控制中提出了对称交叉耦合式同步控制方案。Masayoshi Tomizuka等[9]研究了等同式自适应前馈控制下，双直流电机的运动同步问题。

目前同步控制研究主要集中于控制算法与控制策略方面，对同步控制系统在不同工况下的动态特性辨识问题涉及较少。本研究以功率谱估计为基础，首先对双液压马达同步系统各工作点频率特性的非参数模型进行辨识，形成定量反馈设计模板；然后运用定量反馈设计方法对双液压马达同步驱动系统的交叉耦合式同步控制器进行了研究，最后进行了同步误差实验验证。

1　双液压马达同步控制系统及其功率谱估计

1.1　交叉耦合式同步控制方案

双液压马达同步驱动系统交叉耦合式控制框图如图1所示。图中，r(s)为输入向量，e(s)为误差向量；G(s) 为前向控制器矩阵；W(s)为耦合控制器矩阵；n(s)为耦合控制器输出向量；u(s)为控制器总输出向量；P(s)为双马达传递函数矩阵；θ(s)为系统输出向量，分别对应于：

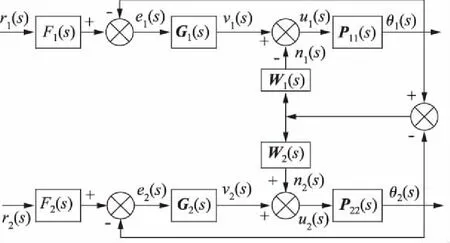
图1　双液压马达交叉耦合式同步控制系统框图

由图可知，双液压马达交叉耦合式同步系统的闭环传递函数矩阵为：

其中，

P11(s)·G1(s)·F1(s)

P22(s)·G2(s)·F2(s)

Δ′={1+P11(s)·[G1(s)+W1(s)]}·

{1+P22(s)·[G2(s)+W2(s)]}-

P11(s)·W1(s)·P22(s)·W2(s)

1.2　功率谱估计系统模型

1) 功率谱估计原理

假设H是一个线性时不变系统，输入信号为X(n)， 输出信号为Y(n)，计算输入与输出信号的互相关函数，可以得到下面的公式(因为X(n)和Y(n)都是实序列,故省去复数的共轭运算)。

RXY(m)=E{X(n)Y(n+m)}=RX(m)·h(m)

等式两边作傅立叶变换，得到:

PXY(ω)=PX(ω)H(ω)

所以只要计算出互谱密度PXY(ω)和功率谱PX(ω)，就可以得到H(ω)的辨识结果为：

(1)

但是待测的输出信号也可能被噪声信号污染。这时的输入输出互相关函数为：

RXY(m)=E{X(n)·[Y(n+m)+N(n+m)]}

=RX(m)·h(m)+RXN(m)

对应的傅立叶变换为：

PXY(jω)=PX(ω)H(jω)+PXN(jω)

为了消除在系统输出端噪声信号的影响，可以通过计算输入输出信号的相干函数γ2(ω)来评价对应频率值处频率响应数据的可靠性：

一般取满足相干函数为0.8<γ2(ω)<1之间频率处对应的频率响应数值为模板数据。

2) 闭环系统辨识

功率谱估计原理是针对开环系统提出的，对于闭环系统需做相应的公式转化。闭环辨识如图2所示。图中，平稳的测试信号X(s)是能观测的，它与噪声N(s) 不相关，那么X(s)就可作为整个闭环系统的独立的输入变量。如图所示，可获得输出为：

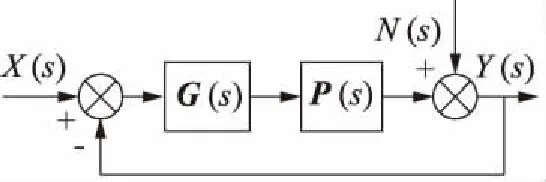
图2　闭环辨识图

对于闭环系统H(s)，其传递函数可表示为：

通常控制器的传递函数G(s)是已知的，则所要确定的传递函数P(s)的参数就可间接地由求解上式获得，故开环系统频率特性的计算公式为：

(2)

其中，i为对应的频率序号，i∈[1,…,n]

3) 双液压马达非参数模型辨识结果

运用上述功率谱估计方法的式(1)和式(2)，以2°间隔，对工作点范围[-12° 12°]进行辨识，可以分别得到马达1和马达2在该工作点范围内非参数频率特性模型，如图3a、3b所示。图中频率范围为[1.256,3.768,8.792,13.816,18.84,26.376,31.4,37.68,47.428,54.008,69.08,79.128,87.92,97.968,109.272]rad/s，各个数字对应符号集合表示该数字对应频率下各个工作点的频率响应。

图3　双液压马达非参数频率特性模型

2　控制器设计

2.1　性能指标边界

双液压马达同步系统性能指标为：

(1) 稳定性：相位裕度37°，幅值裕度8.7 dB；对应的QFT性能指标边界为鲁棒裕量边界：

(3)

(2) 同步误差：在峰峰值1°正弦信号输入下，5 Hz范围内，两马达输出最大误差小于0.06°，即:

εmax=|θ1-θ2|≤0.06°=L

(4)

L为同步误差指标。式(4)同步误差时域指标对应的频域形式为：

(5)

L1≤α2/α1≤L2

(6)

其中，α1为马达1控制通道幅频特性对应实数值；α2为马达2控制通道幅频特性对应实数值；φ1为马达1控制通道相频特性；φ2为马达2控制通道相频特性；且φ2=φ1+Δφ。

(3) 交叉耦合式同步系统稳定性条件：

图1中，以v(s)为输入，θ(s)为输出的耦合控制器内环等效传递函数矩阵为：

(7)

其中，

Δ=1+P22(s)·W2(s)+P11(s)·W1(s)

由定量反馈理论2×2系统稳定性判别引理4.4[10]，且P(s)为最小相位系统可知，控制器应满足以下稳定条件：

|1+G1(s)/π11|-1≤1.58

(9)

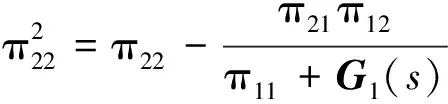
2.2　前向控制器设计

图4为马达1和马达2前向控制器G1(s)，G2(s)的设计图，分别按照SISO QFT控制器设计方法进行。

马达1前向控制器设计为：

(10)

马达2前向控制器设计为：

(11)

图4a、4b中，1所指圈点曲线均指0°工作点名义被控对象，设计中应使该曲线在31.4 rad/s处频率特性相近以保证同步性能。1.256，3.768，8.792，13.816，18.84，26.376，31.4所指曲线为对应数字代表的频率下系统的性能边界。由图4可知，名义对象曲线在各个频率下的响应(圈点)都位于对应频率下性能指标曲线上方，满足稳定性要求。

图4　双液压马达前向控制器设计图

2.3　耦合控制器设计

耦合控制器能够改变闭环传递函数矩阵零极点以改善系统动态响应性能，同时耦合控制器的引入使系统成为2×2 MIMO系统，因此其必须满足式(8)，式(9)定义的稳定条件。满足稳定性条件的耦合控制器设计为：

(12)

图5为耦合控制器稳定性验证图。加入耦合控制器后，系统按照公式(8)和公式(9)所得曲线均位于稳定指标曲线下方，因此系统稳定。

3　同步实验验证

为了验证用以功率谱估计为基础的同步控制器定量反馈设计方法所提出的前向控制器和耦合控制器的同步性能，在双液压马达同步实验台上对[-12° 12°]范围内各工作点分别进行了峰峰值1°正弦信号在1 Hz，3 Hz，5 Hz同步误差验证实验。

图6以0°工作点为例， 给出了双液压马达同步系统在该工作点下分别对1 Hz，3 Hz，5 Hz峰峰值为1°正弦输入信号的响应。图中，点划线1为给定输入信号，2实线为马达1输出信号，虚线3为马达2输出信号，对应两马达同步误差绝对值分别为：0.047°，0.048°，0.050°，满足同步误差指标。

图5　耦和控制器稳定性验证图

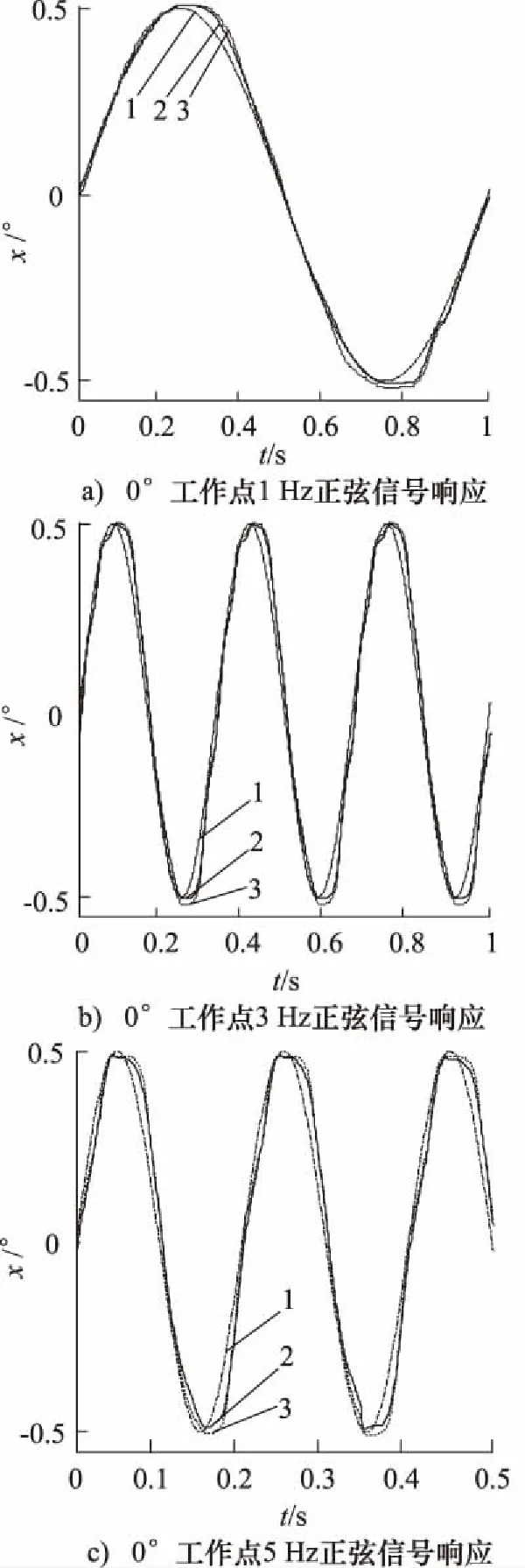
图6　双液压马达同步系统0°工作点正弦信号响应

表1所示为双液压马达同步系统在-12°～12°工作点范围内，各工作点在1 Hz，3 Hz,5 Hz正弦信号下的同步误差。从表中可知，除极个别点外，双液压马达同步系统在前向控制器和耦合控制器控制下都能够满足所要求的同步性能指标要求。

表1　各工作点在1 Hz,3 Hz,5 Hz正弦信号下同步误差

4　结论

针对双液压马达同步控制问题，提出一种以功率谱估计为基础的同步控制器定量反馈设计方法，并对用该方法设计出的控制器进行了同步实验验证，证实了所设计出控制器的有效性。同步控制器设计方法具有控制器设计准确，设计过程透明的特点。

参考文献：

[1]赵克定，王长坤，李尚义.双电液伺服马达同步控制系统的研究[J].机床与液压,1991，(1)：18-23.

[2]李军伟，赵克定.液压仿真转台中框等同式同步控制系统的研究[J].液压与气动,2004,(12):31-32.

[3]王铠,王占林,付永领,纪有哲.大型卧式仿真转台智能化同步—干扰控制[J].机械工程学报,2006,42(10):233-238.

[4]王铠,王占林,付永领,李万国.电液仿真转台控制系统设计与仿真研究[J].宇航学报,2007,28(1):178-182.

[5]王益群,王燕山.气液联合多通道同步加载比例复合控制系统[J].机械工程学报,2005,41(10):180-184.

[6]P Sarachik, J R Ragazzini. A Two Dimensional Feedback Control System[J].Trans.AIEE,1957,76(2):55-61.

[7]Y Koren, J Ben-Uri. Digital Control of Multi-axial Motion System[C].Proceedings of IFAC 5thWorld Congress. Paris,1972,(1):1-27.

[8]Yaram Koren. Cross-coupled Biaxial Computer Control for Manufacturing Systems[J].Journal of Dynamics Systems, Measurement, and Control,1980,(102):265-272.

[9]Masayoshi Tomizuka, Jwu-Sheng Hu, Tsu-Chih Chiu, Takuya Kamano. Synchronization of Two Motion Control Axes Under Adaptive Feedforward Control[J].Journal of Dynamic Systems,Measurement and Control,1999,14(2):196-203.

[10]Oded Yaniv. Quantitative Feedback Design of Linear and Nonlinear Control Systems[M]. Massachusetts: Kluwer Academic Publishers, 1999.