基于拟蒙特卡罗方法的Copula-GARCH类模型在外汇风险计算中的应用

王梦媛 邹玉梅

（山东科技大学统计与金融系，山东 青岛 266590）

随着我国外汇市场不断发展与完善，外汇市场投资已成为继股票市场投资后的第二大投资市场[1]，因此外汇风险管理有其重要意义。为了更好的把握金融市场各外汇的风险，需运用适当的方法来刻画金融历史数据与波动的相关结构，同时还需在风险估计方法上加以改进。高江[2]选择了不同类别的Pair-Copula函数构建藤Copula，运用蒙特卡罗模拟方法计算多资产投资组合的VaR，并与传统方差-协方差风险管理方法做比较显示更优。Niederreiter[3]系统地介绍了拟蒙特卡罗方法和伪随机数，Levy[4]在积分计算中对比拟随机序列与伪随机序列并提出拟随机序列在风险评估领域是更有效的工具。罗付岩等[5]将低差异性数列应用于金融计算中，通过数值实验表明低维时拟蒙特卡罗方法比蒙特卡罗方法精度更高、速度快。

1 拟蒙特卡罗方法

蒙特卡罗方法产生的随机数为伪随机数，具有聚集性的特点，同时也有收敛速度慢、计算量大等缺陷[5]。拟蒙特卡罗方法也称低差异序列法，它类似于蒙特卡罗方法，但它采用确定性的低差异性序列代替伪随机数序列。拟蒙特卡罗方法避免了随机数的聚集特性，并加快了收敛速度。由于低偏差序列所产生的点能较均匀的分布在积分区域内，从而避免了伪随机数的聚集性。因此拟蒙特卡罗方法能很好地应用于模拟计算中[6]。本文考虑的低差异序列是Halton序列。

Halton序列的产生需要首先选出一个数M作为基底。若生成维度为i的序列，则在质数集合中取第i个质数为基底。每个自然数n都可唯一分解成下式：

其中 0≤di＜M，再将上式各项系数代入式（1）：

转换后得到的Halton序列中的随机数。

2 Copula-GARCH类模型

Copula理论的是由Sklar在1959年提出的，可以将任意一个n维联合累积分布函数分解为n个边缘累积分布和一个Copula函数。边缘分布描述的是变量的分布，Copula函数描述的是变量之间的相关性[7]。

2.1 二元Copula函数的定义

二元Copula函数是具有以下性质的函数C(·,·)[8]：

（1）定义域为：I2，即[0,1]2；

（2）C(·,·)有零基面（grounded）且是二维递增（2-increasing）的；

（3）对任意变量 u,v∈[0,1]，满足：C(u,1)=u 和 C(1,v)=v。

Sklar定理[9]：令 H(·,·)为具有边缘分布 F(·)和 G(·)的联合分布函数，那么存在一个 Copula 函数 C(·,·)满足：

若 F(·)，G(·)连续，则 C(·,·)唯一确定；反之 F(·)，G(·)为一元分布函数，C(·,·)为相应的 Copula 函数，那么式（3）定义的函数 H(·,·)是具有边缘分布 F(·)，G(·)的联合分布函数。

有多种方法可用于选择适当的Copula函数族来拟合不同的相关结构，如利用λ函数、AIC准则、Kendall秩相关系数、拟合优度检验以及平面等高线图等途径。Brechmann指出对于二元Copula函数，以AIC准则作为选择标准是可靠的[10]，故本文以AIC准则作为选择Copula函数的标准。先利用λ函数选定待选Copula函数的种类，由极大似然法估计参数后，再分别查看这些Copula函数拟合之后的AIC值，选择其中AIC值最小的作为最终模型。

2.2 GARCH 类模型

GARCH类模型能比较好的描述金融收益率波动的动态变化特征，捕捉丛集效应和非对称性效应[11]。GARCH(p,q)模型的一般表达式为：

式（4）、式（5）中，p≥0，q＞0；ω＞0，αi≥0，i=1,2,…,p，βi≥0，i=1,2,…,q.

GARCH(p,q)模型描述的收益率波动是完全对称的，但有时收益率会呈现出一种非对称性的特征。EGARCH模型是描述波动的非对称效应常用模型之一。

EGARCH(p,q)模型方差方程表达式为：

式（6）中只要γ≠0就存在非对称效应。

3 实证研究

取每日人民币对美元、人民币对英镑外汇汇率中间价为样本数据，采用对数收益率，时间范围为2010年11月1日至2014年5月27日，共864组数据。数据来源于国家外汇管理局网站。

3.1 Copula-GARCH类模型拟合收益率分布的估计结果

由表1中J-B统计量的伴随概率可知，在置信水平为5%时，两种外汇收益率序列均不服从正态分布，序列表现出不同程度的尖峰厚尾性和非对称性，且检验具有ARCH效应，对两种外汇收益率序列分布进行GARCH(1,1)和EGARCH(1,1)建模。

表1 外汇收益率序列的统计特性

利用GARCH类模型提取相应的标准化残差，并对其概率积分变换后得到的序列进行K-S检验。从表2中可知，在5%的显著水平下，本文所建立的GARCH类模型很好地拟合了两种外汇收益率序列的分布。

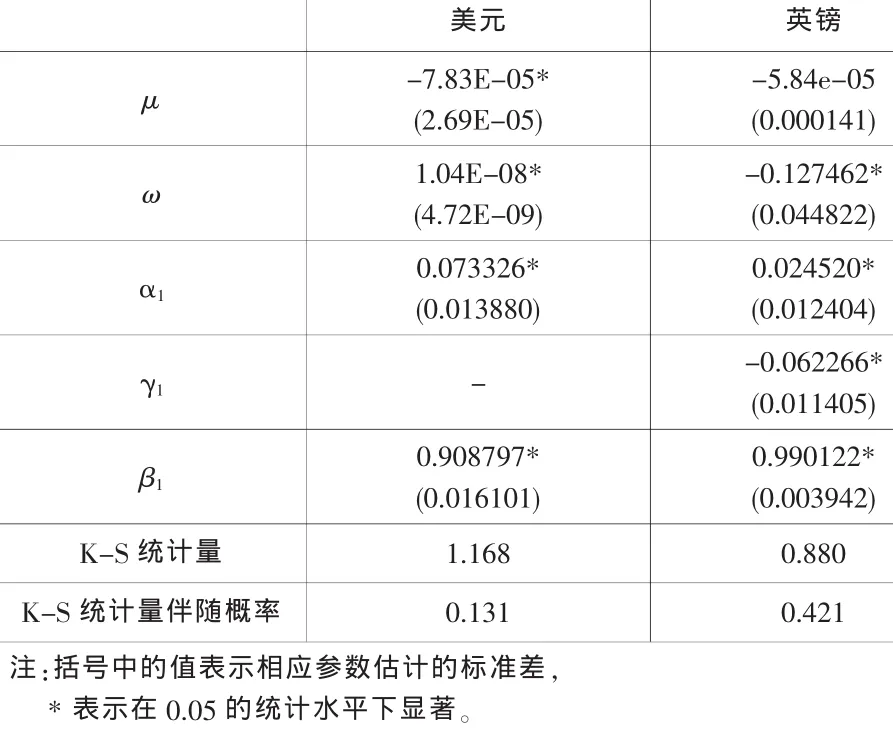
表2 GARCH类模型参数估计及K-S检验结果

计算两种外汇收益率间的Kendall秩相关系数τ=-0.249，本文采用Frank Copula拟合两种外汇的相关结构，利用极大似然估计法得到参数 θ=-2.485486。

3.2 投资组合VaR预测

投资组合中美元、英镑权重分别为β和1-β，利用拟蒙特卡罗方法，重复模拟10000次得到所构建的Copula-GARCH类模型二维仿真数据后，将其还原为资产的收益率数据，进而得到损失序列。由损失序列的经验分布，给定置信度1-α得到投资组合的VaR值。

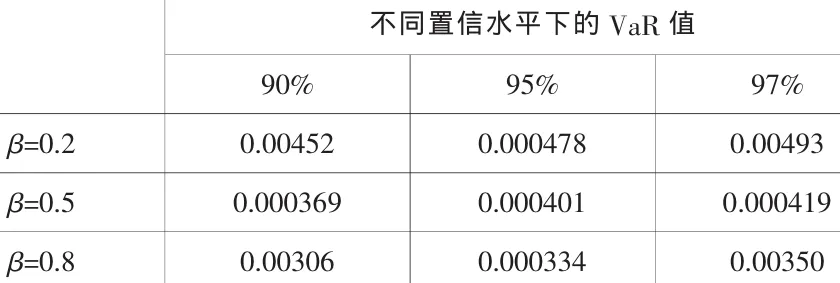
表3 VaR值的估计结果

从表3中结果可以看到在相同置信水平下，随着美元投资比例上升，投资组合的VaR值不断下降，这体现了美元作为国际支付、结算以及投资的主要货币，其价格波动的相对稳定状态。

4 结束语

本文采用Copula-GARCH类模型对两种外汇收益率序列相关结构进行建模。经实证研究，验证了其收益率序列尖峰厚尾且具有条件异方差的特性，本文构建的模型达到了较好的拟合效果。同时利用Halton序列实现了对收益率数据的仿真模拟，预测了不同投资组合的VaR值。Halton序列对维数变化较敏感，其低差异特性会随维数增加而退化，因此在模拟高维变量时可考虑采用其他低差异序列，如Fature序列和Sobol序列。

［1］张岩.外汇投资组合决策研究[D].天津:天津财经大学,2008.

［2］高江.藤Copula模型与多资产投资组VaR预测[J].数理统计与管理,2013,31(2):247-258.

［3］Niederreiter H.Quasi-Monte Carlo methods and pseudo-random numbers[J].Bulletin of the American Mathematical Society,1978,84(6):957-1041.

［4］Levy G.An introduction to quasi-random numbers[DB/OL].http://www.nag.co.uk/IndustryArticles/introduction_to_quasi_random_numbers.pdf.2002.

［5］罗付岩,徐海云.拟蒙特卡罗模拟方法在金融计算中的应用研究[J].数理统计与管理,2008,27(4):605-610.

［6］王宏梅.风险度量中的拟蒙特卡罗方法[J].中国水运:学术版,2006,6(11):159-160.

［7］韦艳华,张世英.Copula理论及其在金融分析上的应用[M].北京:清华大学出版社,2008:1-77.

［8］Nelsen R B.An Introduction to Copulas[M].New York:Springer,2006:10-11.

［9］Sklar A.Fonctions de repartition à n dimensions et leurs marges[J].Publication de l’Insititut de Statistique de l’Université de Paris,1959(8):229-231.

［10］杜子平,汪寅生,张丽.基于混合C藤Copula模型的外汇资产组合VaR研究[J].技术经济与管理研究,2013,32(6):99-103.

［11］龚锐,陈仲常,杨栋锐.GARCH族模型计算中国股市在险价值(VaR)风险的比较研究与评述[J].数量经济技术经济研究,2005(7):67-81.