多尺度分割对脑连接组分析的影响

靳聪，林岚，付振荣，宾光宇，高宏建，吴水才

北京工业大学 生命科学与生物工程学院，北京100124

多尺度分割对脑连接组分析的影响

靳聪，林岚，付振荣，宾光宇，高宏建，吴水才

北京工业大学 生命科学与生物工程学院，北京100124

脑连接组分析可以帮助我们认识、分析人类的大脑。为探究多尺度分割对脑连接组分析的影响，本文从3个尺度（32个节点，128个节点和512个节点）对脑网络中的特征进行分析，发现了稳定存在的小世界特征，以及一些网络特征的变化趋势。如最短路径长随节点个数的增加而增加，聚类系数随节点个数的增加而减少，节点度呈现先上升后下降的趋势。此外，我们发现多尺度分割对于网络的模块化结构影响不显著，但对于网络中的hub节点有一定的影响。

磁共振成像；脑连接组；多尺度分割模板；弥散张量成像；脑网络特征

0 前言

大脑是世界上最为复杂的生理结构之一，它由约1011个神经元和1015个突触连接而成[1]。大脑中复杂的连接模式和动态变化给脑研究带来了极大的挑战。Sporns教授[2]在2005年首次提出了脑连接组的概念，它将大脑定义为由节点和边组成的网络，即脑网络。在连接组的概念中，大脑的脑区被抽象为一个个节点，而脑区之间的连接关系则被抽象成为一条条边。脑连接组的出现，使得人们可以通过网络分析进一步了解大脑的结构及其运行机制。研究人员发现通过神经影像技术，利用脑连接组的分析方法，一些神经退行性疾病如阿尔茨海默症[3-4]，癫痫[5]，精神分裂症[6]等可以进行早期预测，这给神经退行性疾病的诊断与治疗带来了新的希望。

弥散张量成像（Diffusion Tensor Image，DTI）是目前广泛应用于神经退行性疾病研究的一种神经影像技术，它通过追踪水分子的扩散进而显示白质纤维束的分布。由于这一过程是动态的且无侵害性， DTI图像在脑损伤的研究中发挥了重要作用。基于图论的复杂网络分析是目前DTI数据处理中常用的分析方法，其处理流程可大致可分为以下几步。首先，构建脑网络：利用分割图谱将大脑划分成不同大小、不同数量的脑区；接着，将脑区之间的连接关系添加到节点上，从而形成脑网络；其次，通过分析脑网络以获取脑区之间的网络拓扑关系；最后，通过统计分析得到脑网络特征。上述分析步骤中，图谱划分脑区其中最关键的处理步骤。研究表明，分割尺度的改变将会导致脑网络特征的改变[7]。

脑连接组的研究尺度可分为三大类，分别为神经元水平的小尺度，神经元集群水平的中间尺度和大脑脑区水平的大尺度。在小尺度，节点的定义非常明确，即一个节点对应于一个神经元。但受到神经影像技术水平的限制，目前大部分的研究是基于大脑脑区水平的大尺度。而在大尺度研究中，节点的划分尚未明确，节点的个数也由几十个到上万个不等。如表1所示，一些研究采用不同的分割尺度对脑连接组进行分析，如Achard等[8]的研究选择将大脑划分为90个节点，而van den Heuvel[9]等的研究则选择将大脑划分为10000个节点。他们的研究结果表现出了显著的网络特征差异。分割尺度的大小会给网络特征带来何种影响？本研究基于此目的，探究不同尺度节点划分对脑连接组分析的影响，并找出不同分割尺度的脑网络特征之间的关系。

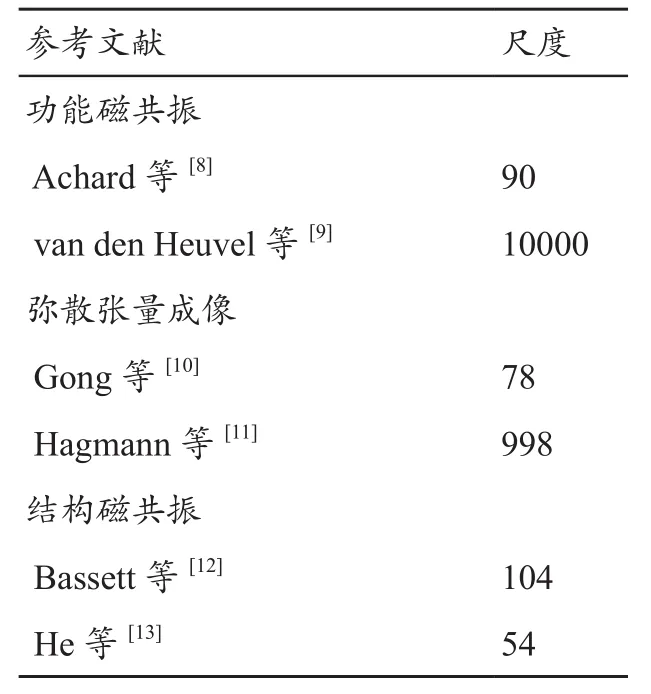
表1 不同尺度的脑区划分

1 材料与方法

1.1 研究对象与数据获取

本研究，年龄范围为50～75岁，其中男性36例，女性39例。受试对象的纳入标准是：无精神异常史及其他影响中枢神经系统的疾病，简易精神状态量表检查评分均≥25分，汉密尔顿抑郁评定量表≤10分。

本研究数据采用GE SignaⅡ3.0T核磁共振扫描仪，DTI图像采用单次激发自旋回波平面成像（Echo-Planar Imaging, EPI）序列。其扫描参数为：8个方向无扩散敏感梯度b = 0 s/mm2，51个方向施加扩散敏感梯度b = 1000 s/mm2，TR = 12500 ms，TE = 71 ms，矩阵：128 × 128，FOV = 250 mm ×250 mm，层厚= 2.6 mm。所有的磁共振成像数据都在美国亚利桑那大学附属医院采集。

1.2 图像处理

1.2.1 预处理和生成多尺度均匀分割模板

原始数据的DICOM格式被转换为NIFIT格式，以便于后期的图像处理。为了去除头动和图像变形给数据带来的影响，数据将进行电涡流和头动校正。预处理流程如图1所示。

图1 预处理流程图

本研究在划分脑区时使用的图谱为均匀分割的随机图谱。该随机图谱依据二值化的AAL模板，将全脑均匀分割成N个体积大小相等的脑区[14]。本研究中共生成三个不同尺度的随机图谱，N值分别为32，128和512。

1.2.2 获取脑网络连接模式

PANDA软件[15]的处理步骤为：首先，使用随机图谱（32脑区节点，128脑区节点和512脑区节点）将大脑划分成不同数量的脑区；然后使用确定性追踪算法获取节点之间的连接边，构建脑网络模型；依据脑网络模型，得出连接矩阵FA（平均各向异性矩阵），FN（纤维束数量矩阵），和FL（平均纤维束长度矩阵）。流程图如图2所示。

图2 获取脑网络连接模式流程图

1.3 网络处理

1.3.1 网络拓扑特征

本研究采用基于图谱的复杂网络分析方法进行网络拓扑特征的计算。通过脑连接工具箱（Brain Connectivity Toolbox）软件，获得3个全局网络特征和3个局部网络特征[16]，具体计算公式见表2。

表2 网络特征公式

节点中心度（bi）bi表示i节点对于信息传递的影响；ρhj 表示在节点h和节点j中最短路径的个数；ρhj(i)h节点和j节点的最短路径中经过i节点的个数。全局参数全局最短路径长（Lp）Lp表示网络中信息传递时路径的效率；Lij表示在成对的节点(i, j)中的最短路径长。全局聚类系数 （Cp）Cp表示网络中局部集群或是小集团的程度，可以表征网络的信息传递效率；Ci表示节点i的聚类系数值。度（Kp）Kp表示全脑节点之间的连接程度。Ki表示节点i的节点度。

1.3.2 随机网络和小世界特征

规则网络具有较高的集群系数和较长的最短路径长度，而随机网络拥有较低的集群系数和较短的最短路径长度。小世界网络兼具高集群系数和最短路径长度，具有相对高的局部效率和全局效率。它由真实网络和随机网络的两个比值来表示：λ（最短路径长之比）和γ（聚类系数之比）。小世界网络具有最短路径长之比接近1，聚类系数之比远大于1的特征[17]。为计算λ和γ，我们首先构建了随机网络模型（ER模型），并计算出ER模型的两个网络参数：最短路径长度（Lr）和聚类系数（Cr）。最后计算出小世界特征λ=Lp/Lr和γ=Cp/Cr。

1.4 Hub节点

Hub节点是网络中最为重要的节点，大量其它节点之间的信息传输都需要经过该节点。若该节点受到损害，则整个网络的效率会严重降低。分析不同图谱的hub节点变化情况可以在一定程度上展示分割尺度对脑网络的影响。

较高的节点度、节点中心度和较低的聚类系数是hub节点在脑网络中的突出特征，依据这个特征，我们计算了各个节点的权重[18]。即节点度和节点中心度参数值较大的节点得到较高权重；与此同时聚类系数参数值较小的节点获得较高权重。将三个参数的权重汇总排序后，就可以根据总权重的高低确定hub节点。最终，我们按照前1%和前5%的比例值分别挑选出相对应的hub节点（如512图谱：前1% hub节点为5个节点，前5% hub节点为26个节点）。

1.5 模块

模块（module）是网络中的节点集群，它表现为模块内部节点间连接紧密，但模块与模块间的节点连接较为稀疏。脑网络模块化结构的研究，可以帮助我们理解网络中节点集群的分布，从而进一步了解节点个数对于整个脑网络的影响。Newman和Girvan[19]教授于2004年首次提出了模块的计算公式：

其中，m是模块组织结构，nm是模块总个数，s代表当前模块，hs是当前模块s节点之间边的加权值之和，L是所有边的加权总和，Ts是当前模块s所有节点的加权和。Q(m)为最大网络模块结构，当Q(m)取得最大值时，则得到最优化的模块结构。

2 结果

2.1 全局网络特征

随着节点个数的增加，网络特征也随之发生改变。在本研究中，我们首先对最短路径长、聚类系数和度进行了研究。实验结果显示（图3），随着尺度的增加，最短路径长随之增加，聚类系数随之减少。值得注意的是，度呈现先上升后下降的趋势，而标准化的度呈现下降的趋势。ANOVA分析结果显示节点个数对最短路径长（F(2,222)=6222.471，P＜00.01)、聚类系数（F(2,222)=2177.013， P＜0.001)、度（F(2,222)=521.047，P＜0.001）和标准化的度（F(2,222)=10063.534，P＜0.001）有显著影响。

图3 网络特征图

2.2 小世界特征

小世界特征可以由λ和γ两个值来表示。实验结果显示三个图谱的最短路径长之比均接近1，聚类系数之比均大于1。此外，研究发现，随着节点个数的增加，λ和γ也随之增加。如图4所示。ANOVA分析结果显示节点个数对λ（F(2,222）=277.142，P＜0.001）和γ（F(2,222)=180.554，P＜0.001）有显著影响。

图4 小世界特征

2.3 hub节点

Hub是网络中的关键节点，本研究发现分割尺度的差异将直接导致hub节点的差异。如图5所示。

图5 三个图谱hub节点展示图，该展示图从左到右依次为左视图，俯视图和正视图。

2.4 模块

真实脑网络具有若干个相对独立而又相互联系的模块。模块化结构使得具有不同功能的模块可以在不影响其它模块的情况下相对独立的演化发展。同时，模块化的组织结构也可以帮助我们区分脑区节点的不同角色和地位。通过Newman计算公式，我们计算了三个尺度（32脑区节点、128脑区节点和512脑区节点）的模块化组织结构，并将这些结果可视化，如图6所示。此外，为更进一步的探究网络节点的个数对于模块化组织结构的影响，我们计算了三个尺度模块化结构的标准化互信息（Normalized Mutual Information，NMI）。结果发现对于32脑区节点和128脑区节点的网络模块化结构，其NMI值为0.9287；对于128脑区节点和512脑区节点的网络模块化结构，其NMI值为0.9022；对于32脑区节点和512脑区节点的网络模块化结构，其NMI值为0.8904。

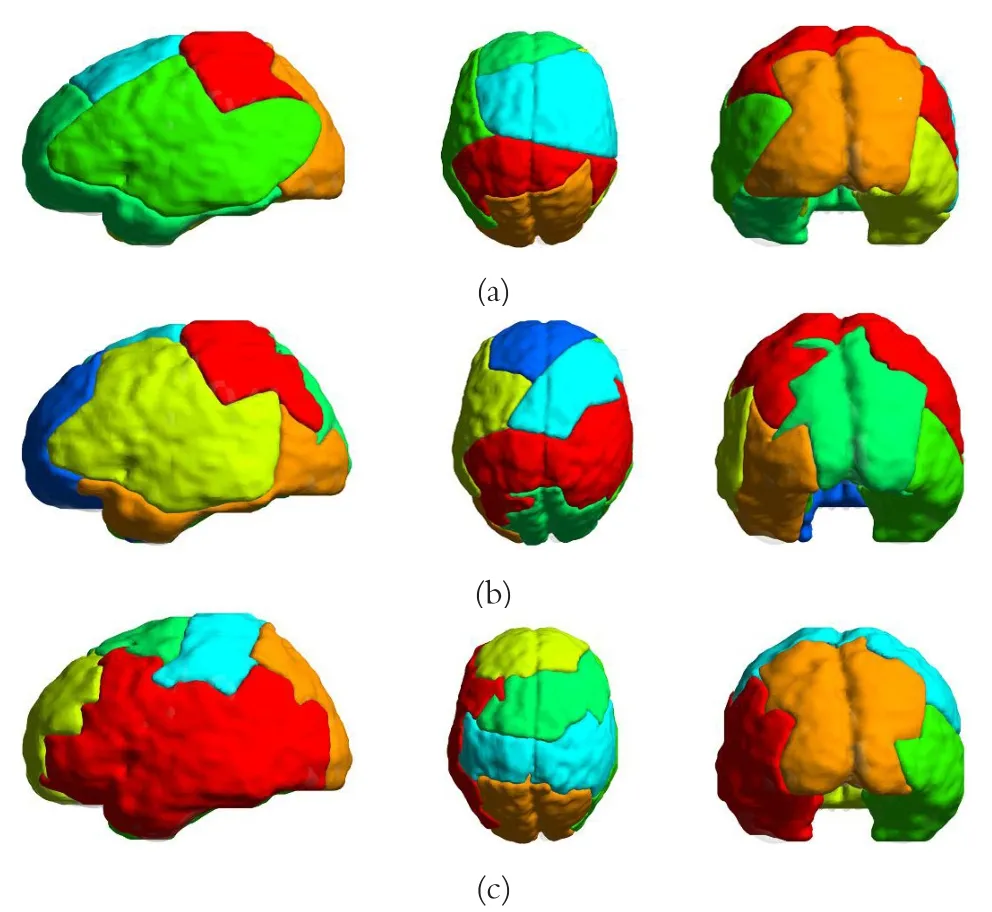
图6 三个图谱模块化结构的展示图

3 讨论

在大尺度的脑连接组网络分析中，脑区划分的尺度还不存在金标准。研究人员采用不同的划分尺度进行了大量的研究，但这些研究结果间往往无法直接进行比较。本研究从3个尺度（32脑区节点，128脑区节点和512脑区节点），4个方面（网络特征，小世界特征，hub节点及网络的模块化结构）研究了分割尺度给脑连接组分析带来的影响。研究证实了小世界特征的普遍存在性，即在三个尺度的脑网络中我们均发现λ值接近1和γ值远大于1，此结果与前人的研究结果基本一致[14]。此外，我们在实验中发现，三个脑网络的模块化组织结构较为相近，分割尺度对于脑网络的模块化组织结构没有显著影响，NMI的计算结果从信息论的角度也证实了上述结论。在hub节点的研究中，我们发现，随着尺度的降低，一些在局部网络中起着重要作用的区域性核心节点以及局部网络的信息传递中占据着举足轻重的地位的区域性连接子可能会被检测为hub节点，而在大尺度分割时，这些节点由于位于一些较大脑区中，它们的作用往往被忽略。

与此同时，最短路径长、聚类系数和度与分割尺度间有着紧密的联系。当分割尺度较大时(如将全脑划分为32个脑区)，脑区体积较大，每个脑区往往包含一个或是多个功能区。这些功能区通过相互通讯协同实现大脑的各种功能。此时，脑区间不仅存在着大量近程连接，还存在大量的远程连接。此时虽然脑区节点个数较少，但脑区节点间连通的比例高，度的值也是较大的。而随着分割尺度的减小，脑区总数呈上升趋势。此时表现为近程连接增多而远程连接减少。脑区个数在增多，同时脑区间连通的比例在下降，总的作用是使得度仍然呈现上升趋势。当节点数进一步增大（512个脑区节点），总的脑区数目上升，但每个脑区的体积变小。此时，尽管与每个脑区的相邻的脑区增多，但这些脑区间并不一定存在直接的网络连接，而是通过其它脑区间接连接。此时度更多表现为大量神经元集群所形成的局部网络的连接特性，呈下降趋势。随着脑区节点数目的变化，度表现出非线性的特征。尺度越小，与度相关的一些网络特征就越表现出局域性的趋势。标准化的度显示随着脑区数目的增多，脑区间的连通率在下降。随着脑区间长连接的减少，网络的聚类系数也开始下降。此外，随着脑区个数的增加，两个脑区之间传递信息所需要通过的其他脑区个数随之增加，并且网络中长连接（捷径）减少，最短路径长随之增加。

4 结论

目前，脑连接组的分析是脑科学研究领域中的研究热点。依据不同分割尺度得到的脑网络分析结果，彼此之间很难进行分析验证。分割尺度对于脑连接组影响的研究目前仍处于探索阶段。本研究采用均匀分割的随机模板从3个尺度分析了脑网络中特征的变化，并发现了一些变化趋势和相关结论，为后人在多尺度分割的脑连接组分析方面提供了一些经验。根据结果，我们发现脑区尺度对分析结果存在一定影响。不同分割尺度的网络特征可能会具有不同的生理、病理学意义。较大尺度的脑连接组可能更适合于分析大脑相关功能区的网络活动，而较小尺度的脑连接组则往往包含了大量神经元集群所形成的局部网络的信息。从多个尺度同时对脑网络分析可以帮助我们从不同视角观察网络变化。与此同时，本研究仍存在一些不足，我们采用的随机模板，在划分时并没有考虑到脑区的生理结构和功能，这一点可能会给分析结果带来一定的影响，今后的研究需要对其进行进一步改进。

[1] Pelvig DP,Pakkenberg H,Stark AK,et al．Neocortical glial cell numbers in human brains[J]．Neurobiol Aging,2008,29(11): 1754-1762．

[2] Sporns O,Tononi G,Kötter R．The human connectome:a structural description of the human brain[J]．PLoS Comput Biol,2005,1(4):e42．

[3] Oishi K,Mielke MM,Albert M,et al．DTI analyses and clinical applications in Alzheimer’s disease[J]．J Alzheimers Dis,2011,26: 287-296．

[4] Ortiz-Terán L,Santos JMR,Martín MNC,et al．Currently Available Neuroimaging Approaches in Alzheimer Disease (AD) Early Diagnosis[J]．Intech,2011．

[5] Carlson HL,Laliberté C,Brooks BL,et al．Reliability and variability of diffusion tensor imaging (DTI) tractography in pediatric epilepsy[J]．Epilepsy Behav,2014,37:116-122．

[6] Samartzis L,Dima D,Fusar-Poli P,et al．White matter alterations in early stages of schizophrenia:a systematic review of diffusion tensor imaging studies[J]．J Neuroimaging,2014,24(2):101-110．

[7] Bassett DS,Brown JA,Deshpande V,et al．Conserved and variable architecture of human white matter connectivity[J]．Neuroimage, 2011,54(2):1262-1279．

[8] Achard S,Salvador R,Whitcher B,et al．A resilient,low-frequency, small-world human brain functional network with highly connected association cortical hubs[J]．J Neurosci,2006,26(1): 63-72．

[9] van den Heuvel MP,Stam CJ,Boersma M,et al．Small-world and scale-free organization of voxel-based resting-state functional connectivity in the human brain[J]．Neuroimage,2008,43(3): 528-539．

[10] Gong G,He Y,Concha L,et al．Mapping anatomical connectivity patterns of human cerebral cortex using in vivo diffusion tensor imaging tractography[J]．Cerebral Cortex,2009,19(3):524-536．

[11] Hagmann P,Cammoun L,Gigandet X,et al．Mapping the structural core of human cerebral cortex[J]．PLoS Biol,2008,6(7): e159．

[12] Bassett DS,Bullmore E,Verchinski BA,et al．Hierarchical organization of human cortical networks in health and schizophrenia[J]．J Neurosci,2008,28(37):9239-9248．

[13] He Y,Chen ZJ,Evans AC．Small-world anatomical networks in the human brain revealed by cortical thickness from MRI[J]．Cerebral cortex,2007,17(10):2407-2419．

[14] Zalesky A,Fornito A,Harding IH,et al．Whole-brain anatomical networks:does the choice of nodes matter?[J]．Neuroimage, 2010,50(3):970-983．

[15] Cui Z,Zhong S,Xu P,et al．PANDA:a pipeline toolbox for analyzing brain diffusion images[J]．Frontiers Hum Neurosci, 2013,7(42)．

[16] Rubinov M,Sporns O．Complex network measures of brain connectivity:uses and interpretations[J]．Neuroimage,2010, 52(3):1059-1069．

[17] van den Heuvel MP,Stam CJ,Boersma M,et al．Small-world and scale-free organization of voxel-based resting-statefunctional connectivity in the human brain[J]．Neuroimage, 2008,43(3):528-539．

[18] Ottet MC,Schaer M,Debbané M,et al．Graph theory reveals dysconnected hubs in 22q11DS and altered nodal efficiency in patients with hallucinations[J]．Frontiers Hum Neurosci,2013,7．

[19] Newman MEJ,Girvan M．Finding and evaluating community structure in networks[J]．Phys Rev E Stat Nonlin Soft Matter Phys,2004,69(2):026113．

In fl uence of Multi-Scale Parcellation on Connectome Analysis

JIN Cong, LIN Lan, FU Zhen-rong, Bin Guang-yu, GAO Hong-jian, WU Shui-cai
College of Life Science and Bio-Engineering, Beijing University of Technology, Beijing 100124, China

The connectome analysis can help us to have a better understanding of human brain networks. In order to detect the in fl uence of the multi-scale parcellation on connectome analysis, this paper studied the brain network from three scales(32 nodes, 128 nodes and 512 nodes). The results revealed that small-world property existed over those brain networks, and the network features showed some trends related to the parcellation scale. For example, the shortest path length increased with the decrease of the parcellation scale, clustering coef fi cient decrease with the decrease of the parcellation scale, while the degree increased firstly and then decreased. Additionally, this paper also found that multi-scale parcellation had no signi fi cant effect on the network modularity structure, but had somewhat impact on hub regions.

MRI; brain connectome; multi-scale parcellation; diffusion tensor imaging; brain network features

R197.39

A

10.3969/j.issn.1674-1633.2015.06.004

1674-1633(2015)06-0018-05

2015-03-05

北京市自然科学基金（7143171）资助。

林岚，副教授 。

通讯作者邮箱：lanlin@bjut．edu．cn