基音周期检测的希尔伯特-黄变换方法

焦 蓓，曾以成，毛燕湖

湘潭大学 光电工程系，湖南 湘潭 411105

1 引言

人在发浊音时，声门周期性地打开与闭合，使来自肺部的空气流形成一串周期性的脉冲气流进入声道，这脉冲串的周期称为基音周期。基音周期是语音信号处理中最重要的参数之一，准确地检测基音周期对于高质量的语音合成、语音编码、语音识别及说话人识别有重要意义。近年来，人们从语音信号的时域特性、频域特性、时频混合特性出发，提出了许多基音检测方法，最具有代表性的是自相关法（Autocorrelation Function，ACF）[1]、平均幅度差法（Average Magnitude Difference Function，AMDF）[2]、倒谱法[3]、小波变换法[4-5]及其衍生算法。虽然上述各种方法已经在不同的系统中得到一定程度的应用，但它们都是基于语音的短时平稳假设，不能完全适用于非平稳、非线性的整体语音信号，部分算法还受Heisenberg不确定原理的制约，时频分辨率受到限制。

Hilbert-Huang变换是处理非线性、非平稳信号的新方法[6]，该方法吸取了小波变换多分辨的优势，同时又克服了在小波变换中需要选择基函数的缺点，根据信号本身的特性自适应地对信号进行分解，不需要对信号做短时平稳假设，由于不受Heisenberg不确定原理的制约，时频分辨率比较高；加上瞬时频率的引入，可以从时频两方面同时对信号进行分析，增加了处理信号的灵活性和有效性。近年来，因其在各个领域，如海洋信号分析[7]、地震信号分析[8]、图形图象处理[9]等的成功应用，也开始应用于语音信号处理。

基于传统基音检测法的不足和Hilbert-Huang变换的优势，本文提出基于Hilbert-Huang变换的基音周期检测法。

2 原理及其算法

希尔伯特-黄变换（Hilbert-Huang Transform，HHT）被认为是一种处理非线性、非平稳信号的自适应算法[10-11]。HHT主要包含两个部分：经验模态分解（Empirical Mode Decomposition，EMD）和希尔伯特变换（Hilbert Transform，HT），其中EMD是核心。

经验模态分解往往被称为是一个“筛选”（sifting）过程。这个筛选过程依据信号特点自适应地把任意一个复杂信号分解为一列本征模态函数IMF。每个IMF需要满足如下两个条件[6]：

（1）信号极值点的数量与零点数相等或相差是1；

（2）信号的由极大值定义的上包络和由极小值定义的下包络的局部均值为0。

EMD筛选过程详见文献[1]。通过分解，原始的数据序列可用IMF分量ci(t)以及剩余项rn(t)表示：

EMD将信号x(t)分解为n个IMF，对每个IMF分量 即ci(t)作HT，继而可求取每个IMF的瞬时频率和瞬时幅值信息。这类本征模态函数的瞬时频率（Instantaneous Frequency，IF）有着明确的物理意义。

ci(t)和yi(t)构成解析信号z(t)：

由瞬时幅值ai(t)和瞬时频率ωi(t)可将信号表示为：

式（4）中省略了式（1）中的剩余项rn(t)，因为rn(t)幅值小，不是一个单调函数就是一个常数，对信号分析和信息提取没有实质影响。在时间-频率面上画出每个IMF以其幅值加权的瞬时频率曲线，这个时间-频率分布谱图就是Hilbert谱，记为H(ω，t)。

由式（4）可以看出，Hilbert谱其实就是傅里叶变换的一种扩展。与傅里叶变换中的常数幅值和固定频率相比较，式（4）具有时变的幅值和频率，它更能反应出信号的非线性和非平稳等特征信息。

3 基于HHT的基音周期提取

Hilbert-Huang变换适用于非线性非平稳信号处理，不需要对语音信号做短时平稳的假设，因而不需要对语音信号做分帧加窗的处理，但语音数据的长度太长会影响EMD分解的效率，所以一般还是必须对语音信号分帧，只是分帧的目不再是为了保证帧内数据的短时平稳。

语音学研究表明，基音频率范围在60～500 Hz之间，故在基音检测之前，先将语音信号通过60～900 Hz的数字带通滤波器，下限截止频率为60 Hz可以抑制电源的工频干扰，上限截止频率为900 Hz，不但可以保留基音的一二次谐波，还可去掉高次谐波和大部分共振峰的影响，使基音周期的检测更容易。

语音信号中的浊音段保留着基音的周期信息，其能量比清音段大得多，本文采用短时平均能量作为判断清浊音的标志。设定一个阈值，当短时平均能量大于阈值时，该帧语音判为浊音，并进行基音检测，否则判为清音，将此帧置零。将清音帧和静音帧置零后的语音组成待处理语音做后续处理。

对待处理语音做EMD分解，可自适应的得到不同时间尺度的IMF（这个分解对求解瞬时频率是很有帮助的，因为瞬时频率的方法只对单分量信号有意义，而EMD分解就是把复杂的语音信号分解为许多单分量信号（IMF）之和）。分解后的IMF分量的分布是从高频到低频，小尺度到大尺度，在同一局部时间不会出现相同的频率，但同一个IMF在整个时间段内有可能出现几个不同的频率段。因此，基音周期就可能在不同的时间段处于不同的IMF分量中，所以单一的IMF已经不能单独作为基音的表示，本文采用加权处理。

通过对每个IMF做HT变换，可以得到瞬时频率和瞬时幅值。由于基音频率范围的限制，有用的频率范围为60～500 Hz，其余频率点置零。从图1可以看出，高幅值的imf2分量和res分量周期性比较明显，低幅值的imf1分量周期性相对较弱。图2显示imf2分量和res分量的频率在基音频率的范围内，imf1分量的频率超出基音频率范围。结合图1、图2可知高幅值IMF分量包含大量的基音信息，低幅值IMF分量包含较少的基音信息。文献[12]中提到低幅值部分包含大量的共振峰信息。为了加强基音信息同时减少共振峰影响，采取对IMF分量加权处理的方法，权值由分量的幅值决定。幅值大的对基音贡献大，即权值大，幅值小的对共振峰贡献大，对基音贡献小，即权值小。通过加权不但可以减少共振峰的影响而且可以增强基音信息，给后续基音周期的准确提取奠定了基础。

图1 IMF分量的瞬时幅值图

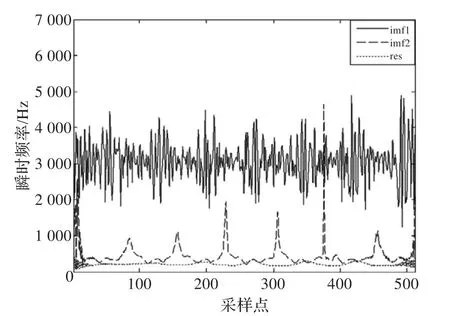
图2 IMF分量的瞬时频率图

为了突出基音周期整数倍点上的峰值，采用自相关的平方做最后的基音周期提取。基于以上分析，具体的基音周期提取流程如图3所示。

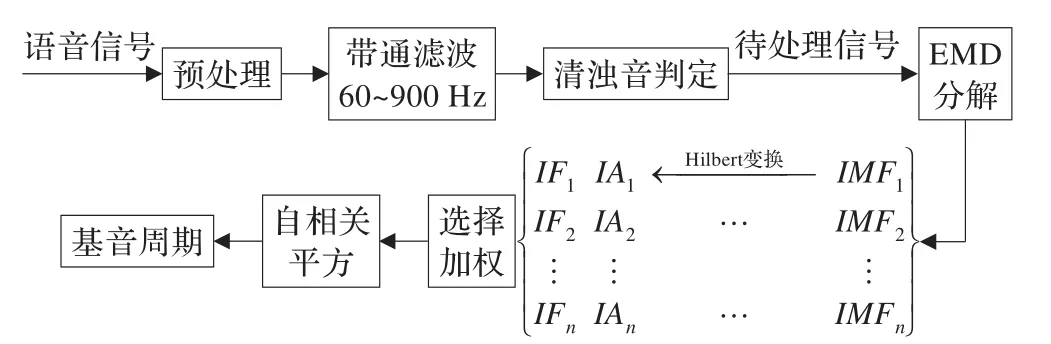
图3 基音提取流程图

图3中的IF为瞬时频率（Instantaneous Frequency），IA表示瞬时幅值（Instantaneous Amplitude）。

4 实验结果与分析

实验所用的原始语音信号如图4（a）所示，语音为普通话汉语拼音元音“a”的四个不同声调的读音，四个声调读的顺序依次为一声、二声、三声和四声。采样频率为8 kHz，量化比特为16 bit。对原始语音分帧，帧长为50点，帧移为50点，进行清浊音判断，令原始语音中的清音帧和静音帧为零。如图4（b）所示。把置零后的语音作为待处理信号，再分帧，帧长取512，帧移取160，分别采用ACF方法、Cepstrum方法和本文提出的方法进行基音检测。

图4 原始语音和待处理语音的波形图

图5、图6和图7是不同方法下检测到的基音轨迹图。图5为ACF方法检测的基音结果，从图可以看出ACF检测结果中存在倍频的半频的错误点；图6为Cepstrum方法检测的基音结果，在语音的端点处存在较多的错误点；图7是本文提出的方法，从图可以看出基音轨迹较平滑，且无倍频和半频的出现，对随机错误点的出现也有一定的抑制作用。且图7可以清楚看出每个字的声调，分别为一声、二声、三声和四声，与给出的语音声调完全相符合（基音的变换模式称为声调）。因此本文提出的方法具有更好的基音检测效果。

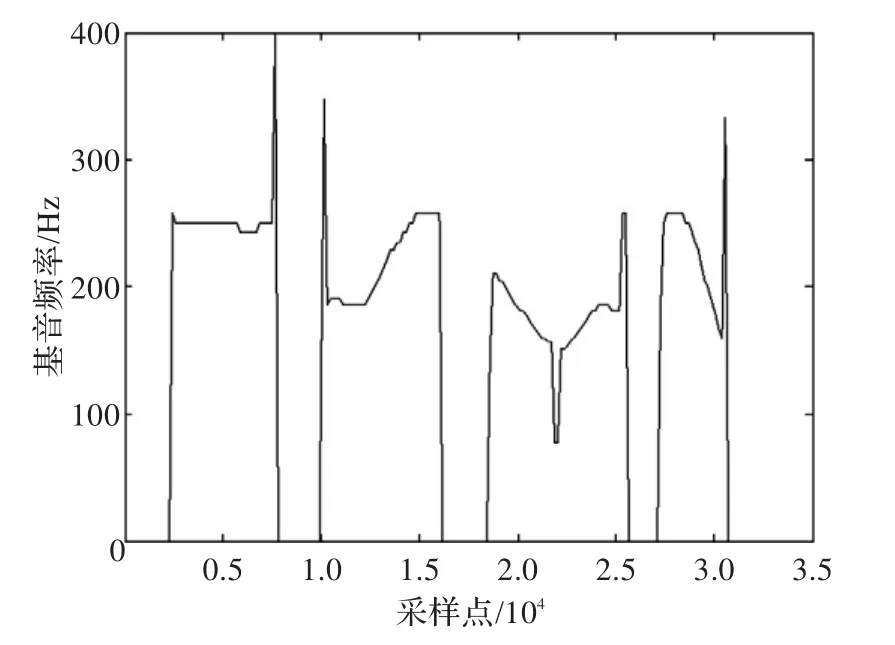
图5 ACF方法检测的基音轨迹

图6 Cepstrum方法检测的基音轨迹

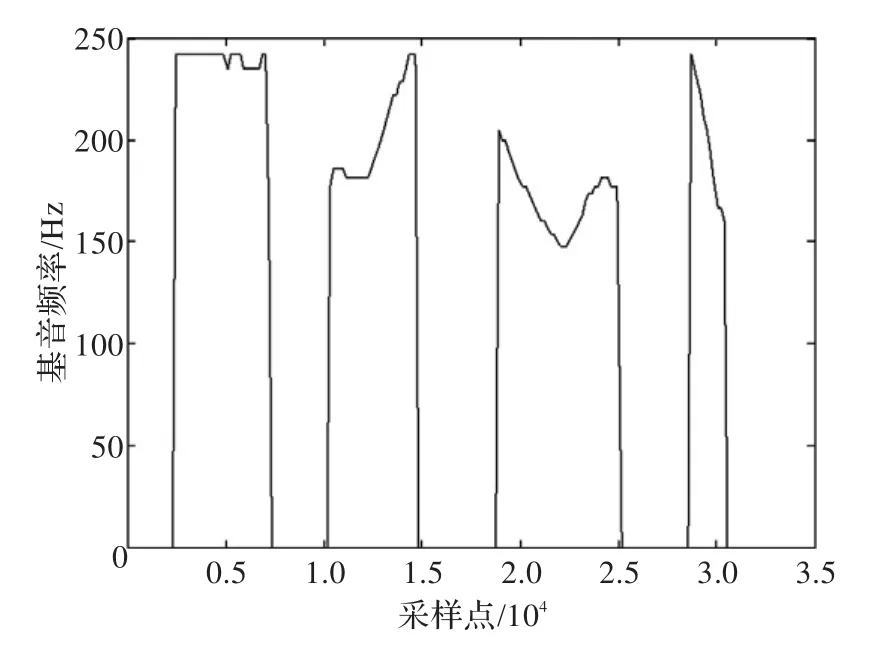
图7 本文方法检测的基音轨迹

在实际生活中，语音信号不可避免的会混入噪声，为了检测本文方法的鲁棒性，在原始语音中加入高斯白噪声，分别采用ACF法、Cepstrum法和本文方法在不同信噪比下对语音信号进行基音检测，检测结果如表1所示。

表1 三种方法在不同信噪比下的基音检测结果 （%）

比较以上的实验结果可见，本文提出的基于希尔伯特-黄变换的基音周期检测法在相同信噪比下较其他两种方法，基音检测的正确率有明显提高。但当信噪比下降为15 dB时，基音检测的正确率只有65.71%，而且随着信噪比的继续降低，这个正确率会减小，即低信噪比下的基音周期检测不是本文的优势，如何提高低信噪比下的基音周期检测是今后需要研究的问题之一。

正确率的高低是检验算法好坏的一个指标，但在实际应用中还要考虑其实时性问题。如图8是ACF方法、Cepstrum方法和本文方法的运行时间对比。

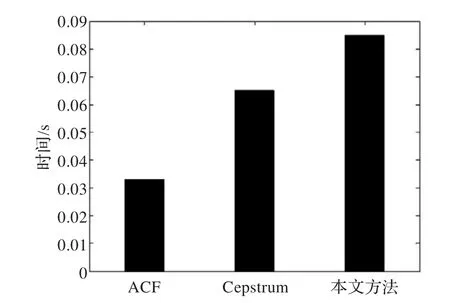
图8 三种不同方法运行时间对比

每种算法都有自己的适用范围。从图8可以看出，ACF检测时间最短，Cepstrum次之，本文方法的检测时间最长，几乎是ACF算法时间的两倍，因此所提算法不适合应用在实时性要求比较高的应用领域。

5 结论

语音是非线性非平稳信号，传统的基音提取方法大部分都是建立在信号短时平稳性假设的基础上，不符合客观实际，因此本文提出了一种基于Hilbert-Huang变换的基音周期检测法。该方法不需要对语音信号进行短时平稳假设，可以根据信号的本身特点，直接从信号本身特点出发将信号自适应的分解为有限个IMF分量，且不受Heisenberg不确定原理的制约，具有很高的时频分辨率。本文方法首先利用短时能量对语音进行清浊音判断，再经过EMD分解为有限个IMF分量，对IMF做Hilbert变换求取瞬时幅值和瞬时频率，这两个瞬时量表现了非平稳信号的内部的真实物理过程，根据基音频率的特点对IMF分量加权求和突出基音周期信息并削弱共振峰影响，最后采用自相关平方法突出基音周期在整数倍点的峰值以便于基音周期的检测。实验表明，本文方法较传统的基音检测法精度有所提高，且鲁棒性较好。但当信噪比较低的时候，基音检测的正确率有所下降，因此如何提高低信噪比下的基音周期检测还需要进一步研究。同时，本文算法较其他两种算法计算时间长，不适合应用在实时性较高的场合。

[1]Krubsack D A，Niederjohn R J.An autocorrelation pitch detector and voicing decision with confidence measures developed for noise corrupted speech[J].IEEE Trans on Acoustics，Speech，Signal Processing，1991，39（2）：319-329.

[2]Ross M J，Shaffer H L，Freudberg R，et a1.Average magnitude difference function pitch extractor[J].IEEE Transactions on Speech and Audio Processing，1999，22（5）：353-362.

[3]Ahmadi S，Andreas S S.Cepstrum-based pitch detection using a new statistical V/UV classify-cation algorithm[J].IEEE Transactions on Speech and Audio Processing，1999，7（3）：333-338.

[4]Cai Runshen，Shi Shaoqiang.A modified pitch detection method based on wavelet transform[C]//Proceedings of the 2nd International Conference on Multi Media and Information Technology.[S.l.]：IEEE ComputerSociety，2010：246-249.

[5]Kadame S，Broudreaux-Bartels G F.Application of wavelet transform for pitch detection[J].IEEE Trans on IT，1992，38（2）：917-924.

[6]Huang N E，Shen Z，Long S R，et al.The empirical mode decomposition and theHilbertspectrum fornonlinear and nonstationary time series analysis[J].Proceeding of Royal Society A，1998，454：903-995.

[7]Huang N E.Review of empirical mode decomposition[C]//Proceedings of International Society for Optical Engineering，2001，4391：71-80.

[8]Zhang Ruichong，Ma Shuo，Safak E.Hilbert-Huang transform analysis of dynamic and earthquake motion recordings[C]//Journal of Engineering Mechanics，2003，129（8）：861-875.

[9]Nunes J C，Bouaoune Y，Delechelle E，et al.Image analysis by bidimensional empirical mode decomposition[J].Image and Vision Computing，2003，21（12）：1019-1026.

[10]沈毅，沈志远.一种非线性非平稳自适应信号处理方法—希尔伯特-黄变换综述：发展与应用[J].自动化技术与应用，2010，29（5）：1-5.

[11]Yan Ruqiang，Gao R X.A tour of the Hilbert-Huang transform：an empirical tool for signalanalysis[J].IEEE Instrumentation&Measurement Magazine，2007，10（5）：40-45.

[12]于凤琴，肖志.利用Hilbert-Huang变换的自适应带通滤波器特性提取共振峰[J].声学技术，2008，27（2）：266-270.

[13]王慧.HHT的方法及其若干应用[D].合肥：合肥工业大学，2009-11.