基于整数规划的投资项目选择模型及Matlab 实现①
孙建英
(青岛理工大学 琴岛学院,山东 青岛266106)
0 引 言
整数规划模型是数学建模中一种常见的很重要的模型,它在汽车生产、钢管下料、指派问题及高校学生选课策略[1]等方面都有广泛的应用,对于一般的整数规划模型,可以利用Lingo 软件求解,但是掌握起来比较困难.随着Matlab 版本的提高,可以直接调用Matlab 优化工具箱(Optimization Toolbox)中的bintprog 或者intlinrog 函数求解0-1整数规划问题,本文通过投资项目的选择问题进行仿真实验.
1 0-1 整数规划的数学模型
0-1 整数规划的数学模型的一般形式为:
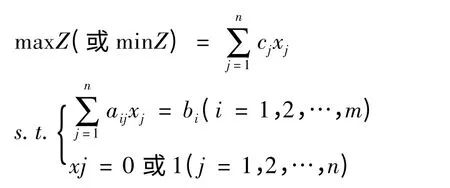
亦可写成矩阵形式

为了能直接调用Matlab 优化工具箱中的函数,0-1 整数规划模型要改为如下标准形式:
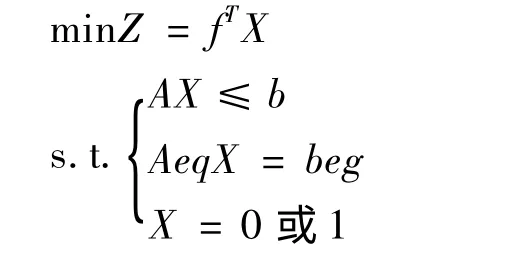
2 Matlab 优化工具箱中的函数
Matlab 优化工具箱中可以用来求解0-1 整数规划问题的函数有两个bintprog 或intlinprog,调用格式如下:
1)函数bintprog 的调用格式

返回的是0-1 整数决策变量和相应的最小目标函数值,f 是由目标函数的系数构成的向量,A,b分别是不等式约束的系数矩阵和右端项,Aeq,beq分别是等式约束的系数矩阵和右端项,X0是整数变量的初始值,options 是控制规划过程的参数系列,调用时要注意参数的位置,如果缺少的话,应该用[]补位.
2)函数intlinprog 的调用格式

intcon 表示整数决策变量的位置,lb,ub 分别表示决策变量的上下限.其它参数的意义不变.
两个函数虽然都能求解0-1 整数规划问题,但是在具体应用过程中发现有三个需要注意的问题,一是对Matlab 版本的要求,前者适用于Matlab7.0 以上,后者适用于Matlab2014A 以上版本;二是对整数变量的个数有要求,当变量的个数比较多时,像文献[2]中需要100*1000 个整数变量的时候,只能用后者求解;三是intlinprog 函数也可以求解一般的整数规划问题,但是bintprog 函数不能.考虑到以上种种,本文实例采用intlinprog 函数为例.
3 实例分析
3.1 投资项目的选择问题的提出
某单位在年初有15 万的资金,有5 个可以投资的项目,每个项目需要的投资额和期望收益如表1,问应投资哪几个项目,期望收益才能保证最大?

表1
(1)甲、丙、戊三个项目需且仅需选择一项;
(2)乙和丁两个项目需且仅需选择一项;
(3)丙和丁项目密切关联,必须先实施丁之后才能实施丙,
3.2 模型的建立
设决策变量x1,x2,x3,x4,x5分别表示甲、乙、丙、丁、戊项目,并且规定xj=1 表示j 项目被选中,xj=0 表示j 项目不被选中,(j=1,2,3,4,5),Z 表示期望收益
目标函数为最大期望收益:maxZ=10x1+8x2+7x3+6x4+9x5,为了能直接调用intlinprog 命令,把目标函数转化为min(-Z)=-10x1-8x2-7x3-6x4-9x5
约束条件有两类,一类是资金总额的限制;一类是项目之间互斥或者先后关系的限制

3.3 Matlab 仿真
Matlab 程序如下:

故只需选择甲项目和乙项目,期望收益为18万元.
3.4 补充说明
intlinprog 命令也可以求解一般的整数线性规划模型,只要把上述程序中的参数ub 也就是整数决策变量的上限不限制为1 就可以了,操作起来非常简单.并且该命令也可以求解混合整数线性规划问题,这时候需要用intcon 来指明哪一个决策变量是整数即可.
[1] 姜启源,谢金星,叶俊.数学模型(第四版)[M].北京:高等教育出版社,2011.
[2] 王颖,高德宏,施恒.DVD 租赁优化方案[J].工程数学学报,2005,22(7):76-84.

